Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Oh, Young-Tak
2008.
q-Analog of the Möbius function and the cyclotomic identity associated to a profinite group.
Advances in Mathematics,
Vol. 219,
Issue. 3,
p.
852.
Maia, Manuel
and
Méndez, Miguel
2008.
On the arithmetic product of combinatorial species.
Discrete Mathematics,
Vol. 308,
Issue. 23,
p.
5407.


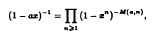
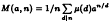 and
and 