Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ward, James R.
1976.
Existence of solutions to quasilinear differential equations in a Banach space.
Bulletin of the Australian Mathematical Society,
Vol. 15,
Issue. 3,
p.
421.

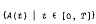 be a family of weakly continuous operators which map
be a family of weakly continuous operators which map