Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T16:51:09.391Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON FREE ACTIONS OF GROUPS ON PRODUCTS OF SPHERES

Part of: Lie groups

Published online by Cambridge University Press:  08 March 2013

JANG HYUN JO  and
JONG BUM LEE
JANG HYUN JO*
Affiliation:
Department of Mathematics, Sogang University, Seoul 121-742, Korea email jlee@sogang.ac.kr
JONG BUM LEE
Affiliation:
Department of Mathematics, Sogang University, Seoul 121-742, Korea email jlee@sogang.ac.kr
*
✉jhjo@sogang.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It has been conjectured that if 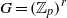$G= \mathop{({ \mathbb{Z} }_{p} )}\nolimits ^{r} $ acts freely on a finite 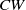$CW$-complex 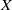$X$ which is homotopy equivalent to a product of spheres 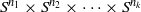${S}^{{n}_{1} } \times {S}^{{n}_{2} } \times \cdots \times {S}^{{n}_{k} } $, then 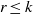$r\leq k$. We address this question with the relaxation that 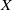$X$ is finite-dimensional, and show that, to answer the question, it suffices to consider the case where the dimensions of the spheres are greater than or equal to 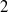$2$.

Keywords

CW-complexfree actionfree ranksolvmanifoldsstrongly polycyclic groups

MSC classification

Secondary: 57S25: Groups acting on specific manifolds 22E25: Nilpotent and solvable Lie groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 2 , October 2013 , pp. 340 - 344
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Adem, A. and Browder, W., ‘The free rank of symmetry of $\mathop{({S}^{n} )}\nolimits ^{k} $’, Invent. Math. 92 (1988), 431–440.CrossRefGoogle Scholar
Adem, A. and Smith, J. H., ‘Periodic complexes and group actions’, Ann. of Math. (2) 154 (2001), 407–435.CrossRefGoogle Scholar
Benson, D. J. and Carlson, J. F., ‘Complexity and multiple complexes’, Math. Z. 195 (1987), 221–238.CrossRefGoogle Scholar
Browder, W., ‘Cohomology and group actions’, Invent. Math. 71 (1983), 599–608.CrossRefGoogle Scholar
Carlsson, G., ‘On the rank of abelian goups acting freely on $\mathop{({S}^{n} )}\nolimits ^{k} $’, Invent. Math. 69 (1982), 393–400.CrossRefGoogle Scholar
Farrell, F. T. and Jones, L. E., Classical Aspherical Manifolds, CBMS Regional Conference Series in Mathematics, 75 (American Mathematical Society, Providence, RI, 1990).Google Scholar
Hanke, B., ‘The stable free rank of symmetry of products of spheres’, Invent. Math. 178 (2009), 265–298.CrossRefGoogle Scholar
Heller, A., ‘A note on spaces with operators’, Illinois J. Math. 3 (1959), 98–100.CrossRefGoogle Scholar
Jo, J. H. and Lee, J. B., ‘Group extensions and free actions by finite groups on solvmanifolds’, Math. Nachr. 283 (2010), 1054–1059.CrossRefGoogle Scholar
Madsen, I., Thomas, C. B. and Wall, C. T. C., ‘The topological spherical space form problem. II. Existence of free actions’, Topology 15 (1976), 375–382.CrossRefGoogle Scholar
Milnor, J., ‘Groups which act on ${S}^{n} $ without fixed points’, Amer. J. Math. 79 (1957), 623–630.CrossRefGoogle Scholar
Mislin, G. and Talelli, O., ‘On groups which act freely and properly on finite dimensional homotopy spheres’, in: Computational and Geometric Aspects of Modern Algebra (Edinburgh, 1998), London Mathematical Society Lecture Note Series, 275 (Cambridge University Press, Cambridge, 2000), 208–228.CrossRefGoogle Scholar
Smith, P. A., ‘Permutable periodic transformations’, Proc. Nat. Acad. Sci. 30 (1944), 105–108.CrossRefGoogle ScholarPubMed
Swan, R. G., ‘Periodic resolutions for finite groups’, Ann. of Math. (2) 72 (1960), 267–291.CrossRefGoogle Scholar
Yalçin, E., ‘Group actions and group extensions’, Trans. Amer. Math. Soc. 352 (2000), 2689–2700.CrossRefGoogle Scholar
Yalçin, E., ‘Free actions of $p$-groups on products of lens spaces’, Proc. Amer. Math. Soc. 129 (2001), 887–898.CrossRefGoogle Scholar