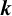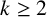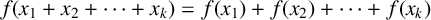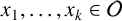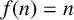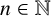1 Introduction
An arithmetic function
![]() $f:\mathbb {N}\to \mathbb {C}$
is multiplicative if
$f:\mathbb {N}\to \mathbb {C}$
is multiplicative if
![]() $f(1)=1$
and
$f(1)=1$
and
![]() $f(mn)=f(m)f(n)$
whenever m and n are relatively prime. Let
$f(mn)=f(m)f(n)$
whenever m and n are relatively prime. Let
![]() $\mathcal {M}$
denote the set of complex-valued multiplicative functions.
$\mathcal {M}$
denote the set of complex-valued multiplicative functions.
A set
![]() $E\subseteq \mathbb {N}$
is an additive uniqueness set of a set of arithmetic functions
$E\subseteq \mathbb {N}$
is an additive uniqueness set of a set of arithmetic functions
![]() $\mathcal {F}$
if there is exactly one element
$\mathcal {F}$
if there is exactly one element
![]() $f\in \mathcal {F}$
that satisfies
$f\in \mathcal {F}$
that satisfies
For example,
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $\{1\}\cup 2\mathbb {N}$
are trivially additive uniqueness sets of
$\{1\}\cup 2\mathbb {N}$
are trivially additive uniqueness sets of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
This concept was introduced by Spiro [Reference Spiro13] in 1992. She proved that the set of primes is an additive uniqueness set of
![]() $\mathcal {M}_0=\{f\in \mathcal {M} \mid f(p_0)\neq 0 \ \text {for some prime}\ p_0\}$
and asked whether other interesting sets were additive uniqueness sets for multiplicative functions. Spiro’s work has been extended in many directions.
$\mathcal {M}_0=\{f\in \mathcal {M} \mid f(p_0)\neq 0 \ \text {for some prime}\ p_0\}$
and asked whether other interesting sets were additive uniqueness sets for multiplicative functions. Spiro’s work has been extended in many directions.
Let
![]() $k\geq 2$
be a fixed integer. If there is only one function
$k\geq 2$
be a fixed integer. If there is only one function
![]() $f\in \mathcal {F}$
which satisfies
$f\in \mathcal {F}$
which satisfies
![]() ${f(x_1+x_2+\cdots +x_k)=f(x_1)+f(x_2)+\cdots +f(x_k)}$
for arbitrary
${f(x_1+x_2+\cdots +x_k)=f(x_1)+f(x_2)+\cdots +f(x_k)}$
for arbitrary
![]() $x_i\in E$
,
$x_i\in E$
,
![]() $i\in \{1,2,\ldots ,k\}$
, then E is called a k-additive uniqueness set of
$i\in \{1,2,\ldots ,k\}$
, then E is called a k-additive uniqueness set of
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
In 2010, Fang [Reference Fang5] proved that the set of primes is a 3-additive uniqueness set of
![]() $\mathcal {M}_0$
. In 2013, Dubickas and
$\mathcal {M}_0$
. In 2013, Dubickas and
![]() ${\breve{\mathrm{S}}}$
arka [Reference Dubickas and Šarka4] generalised Fang’s result to sums of arbitrary primes.
${\breve{\mathrm{S}}}$
arka [Reference Dubickas and Šarka4] generalised Fang’s result to sums of arbitrary primes.
In 1999, Chung and Phong [Reference Chung and Phong3] showed that the set of positive triangular numbers
![]() $T_n=\tfrac 12n(n+1)$
,
$T_n=\tfrac 12n(n+1)$
,
![]() $n\in \mathbb {N}$
, and the set of positive tetrahedral numbers
$n\in \mathbb {N}$
, and the set of positive tetrahedral numbers
![]() ${\textit {Te}}_n=\tfrac 16n(n+1)(n+2)$
,
${\textit {Te}}_n=\tfrac 16n(n+1)(n+2)$
,
![]() $n\in \mathbb {N}$
, were new additive uniqueness sets for
$n\in \mathbb {N}$
, were new additive uniqueness sets for
![]() $\mathcal {M}$
. Park [Reference Park11] extended their work to sums of k triangular numbers,
$\mathcal {M}$
. Park [Reference Park11] extended their work to sums of k triangular numbers,
![]() $k\geq 3$
.
$k\geq 3$
.
In 2018, Kim et al. [Reference Kim, Kim, Lee and Park7] proved that the set of generalised pentagonal numbers
![]() $P_n=\tfrac 12n(3n-1)$
,
$P_n=\tfrac 12n(3n-1)$
,
![]() $n\in \mathbb {Z}$
, is an additive uniqueness set for
$n\in \mathbb {Z}$
, is an additive uniqueness set for
![]() $\mathcal {M}$
. Recently, they showed that the set of positive pentagonal numbers and the set of positive hexagonal numbers
$\mathcal {M}$
. Recently, they showed that the set of positive pentagonal numbers and the set of positive hexagonal numbers
![]() $H_n=n(2n-1)$
,
$H_n=n(2n-1)$
,
![]() $n\in \mathbb {N}$
, are new additive uniqueness sets for the collection of multiplicative functions [Reference Kim, Kim, Lee and Park8]. They also conjectured that among the sets of s-gonal numbers, only the sets of triangular, pentagonal and hexagonal numbers are additive uniqueness sets for
$n\in \mathbb {N}$
, are new additive uniqueness sets for the collection of multiplicative functions [Reference Kim, Kim, Lee and Park8]. They also conjectured that among the sets of s-gonal numbers, only the sets of triangular, pentagonal and hexagonal numbers are additive uniqueness sets for
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Park [Reference Park9] proved that the set of nonzero squares is a k-additive uniqueness set of
![]() $\mathcal {M}$
for every
$\mathcal {M}$
for every
![]() $k\geq 3$
, although it is not a 2-additive uniqueness set [Reference Chung2]. In 2020, he showed that
$k\geq 3$
, although it is not a 2-additive uniqueness set [Reference Chung2]. In 2020, he showed that
![]() $\{p-1 \mid p \ \text { is a prime}\}$
is an additive uniqueness set for
$\{p-1 \mid p \ \text { is a prime}\}$
is an additive uniqueness set for
![]() $\mathcal {M}$
[Reference Park10].
$\mathcal {M}$
[Reference Park10].
Recently, the author [Reference Hasanalizade6] proved that the set of practical numbers is a k-additive uniqueness set of
![]() $\mathcal {M}$
for every
$\mathcal {M}$
for every
![]() $k\geq 2$
.
$k\geq 2$
.
A set
![]() $S\subseteq \mathbb {N}$
is called an additive basis (respectively, an asymptotic additive basis) of order j for
$S\subseteq \mathbb {N}$
is called an additive basis (respectively, an asymptotic additive basis) of order j for
![]() $\mathbb {N}$
if there is a constant j such that every natural number (respectively, every sufficiently large natural number) can be written as a sum of at most j members of S. For example, the classical Lagrange theorem asserts that the set of squares is an additive basis of order
$\mathbb {N}$
if there is a constant j such that every natural number (respectively, every sufficiently large natural number) can be written as a sum of at most j members of S. For example, the classical Lagrange theorem asserts that the set of squares is an additive basis of order
![]() $4$
, and Gauss (1796) proved that the triangular numbers form an additive basis of order
$4$
, and Gauss (1796) proved that the triangular numbers form an additive basis of order
![]() $3$
. The famous binary Goldbach conjecture is equivalent to the assertion that the set of primes is an asymptotic additive basis of order
$3$
. The famous binary Goldbach conjecture is equivalent to the assertion that the set of primes is an asymptotic additive basis of order
![]() $3$
.
$3$
.
A set
![]() $S\subseteq \mathbb {N}$
is called k-automatic if there exists a deterministic finite automaton M that recognises the language of base k representations of elements of S [Reference Allouche and Shallit1].
$S\subseteq \mathbb {N}$
is called k-automatic if there exists a deterministic finite automaton M that recognises the language of base k representations of elements of S [Reference Allouche and Shallit1].
A number is odious if the number of ones in its base 2 representation is odd. The set of odious numbers is 2-automatic. Let
![]() $\mathcal {O}$
be the set of odious numbers, that is,
$\mathcal {O}$
be the set of odious numbers, that is,
Using automata theory, Rajasekaran et al. [Reference Rajasekaran, Shallit and Smith12] proved the following result.
Theorem 1.1 (Rajasekaran et al., 2020).
A natural number is the sum of exactly two odious numbers if and only if it is not of the form
![]() $2\cdot 4^i-1$
for
$2\cdot 4^i-1$
for
![]() $i\ge 0$
.
$i\ge 0$
.
The next theorem, also from Rajasekaran et al. [Reference Rajasekaran, Shallit and Smith12], shows that the set of odious numbers is an asymptotic additive basis of order 3.
Theorem 1.2 (Rajasekaran et al., 2020).
Every natural number
![]() $N>15$
is the sum of three distinct odious numbers.
$N>15$
is the sum of three distinct odious numbers.
We prove the following theorem showing that the set of odious numbers is an additive uniqueness set of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Theorem 1.3. Fix
![]() $k\geq 2$
. The set
$k\geq 2$
. The set
![]() $\mathcal {O}$
of odious numbers is a k-additive uniqueness set of
$\mathcal {O}$
of odious numbers is a k-additive uniqueness set of
![]() $\mathcal {M}$
: if a multiplicative function f satisfies
$\mathcal {M}$
: if a multiplicative function f satisfies
for arbitrary
![]() $x_1,\ldots ,x_k\in \mathcal {O}$
, then f is the identity function.
$x_1,\ldots ,x_k\in \mathcal {O}$
, then f is the identity function.
It would be interesting to see whether a result similar to Theorem 1.3 holds for other classes of automatic sets.
2 Proof of Theorem 1.3
The proof consists of four parts.
Case I:
![]() $k=2$
. It is easy to show by induction that
$k=2$
. It is easy to show by induction that
![]() $f(2^k)=2^k$
for all
$f(2^k)=2^k$
for all
![]() $k\in \mathbb {N}$
, because
$k\in \mathbb {N}$
, because
![]() $f(2)=f(1+1)=2$
and
$f(2)=f(1+1)=2$
and
![]() $f(2^{k+1})=f(2\cdot 2^k)=2f(2^k)$
. Suppose that N is an integer such that
$f(2^{k+1})=f(2\cdot 2^k)=2f(2^k)$
. Suppose that N is an integer such that
![]() $f(n)=n$
for all
$f(n)=n$
for all
![]() $n\le N$
. We show that
$n\le N$
. We show that
![]() $f(N+1)=N+1$
. If
$f(N+1)=N+1$
. If
![]() $N+1\ne 2\cdot 4^i-1$
for
$N+1\ne 2\cdot 4^i-1$
for
![]() $i\ge 1$
, then by Theorem 1.1 there are two distinct odious numbers
$i\ge 1$
, then by Theorem 1.1 there are two distinct odious numbers
![]() $x,y$
such that
$x,y$
such that
![]() $N+1=x+y$
and
$N+1=x+y$
and
![]() $x,y\le N$
. Thus,
$x,y\le N$
. Thus,
![]() $f(N+1)=f(x)+f(y)$
so that
$f(N+1)=f(x)+f(y)$
so that
![]() $f(N+1)=N+1$
. If
$f(N+1)=N+1$
. If
![]() $N+1=2\cdot 4^i-1$
for some
$N+1=2\cdot 4^i-1$
for some
![]() $i\ge 1$
, then
$i\ge 1$
, then
since
![]() $2\cdot 4^i-1=2^{2i+1}-1=\underbrace {11\ldots 1}_{2i+1}{}_2\in \mathcal {O}$
. Therefore,
$2\cdot 4^i-1=2^{2i+1}-1=\underbrace {11\ldots 1}_{2i+1}{}_2\in \mathcal {O}$
. Therefore,
![]() $f(N+1)=N+1$
. Note that in this case we do not use the multiplicativity of f.
$f(N+1)=N+1$
. Note that in this case we do not use the multiplicativity of f.
Case II:
![]() $k=3$
. Clearly,
$k=3$
. Clearly,
![]() $f(3)=3$
and
$f(3)=3$
and
![]() $f(10)=f(2)f(5)=f(2)[2f(2)+1]$
. On the other hand,
$f(10)=f(2)f(5)=f(2)[2f(2)+1]$
. On the other hand,
![]() $f(10)=f(4+4+2)=2f(4)+f(2)$
and
$f(10)=f(4+4+2)=2f(4)+f(2)$
and
![]() $f(4)=f(2+1+1)=f(2)+2$
. Hence,
$f(4)=f(2+1+1)=f(2)+2$
. Hence,
![]() $f^2(2)-f(2)-2=0$
with two solutions
$f^2(2)-f(2)-2=0$
with two solutions
![]() $f(2)=-1$
and
$f(2)=-1$
and
![]() $f(2)=2$
. The first solution yields
$f(2)=2$
. The first solution yields
![]() $f(4)=1$
, which leads to the contradiction
$f(4)=1$
, which leads to the contradiction
 $$ \begin{align*} f(6)& =f(4+1+1)=f(4)+2=3 \\ & =3f(2)=-3. \end{align*} $$
$$ \begin{align*} f(6)& =f(4+1+1)=f(4)+2=3 \\ & =3f(2)=-3. \end{align*} $$
Therefore, we conclude that
![]() $f(2)=2$
. From this, it is easy to check that
$f(2)=2$
. From this, it is easy to check that
![]() $f(n)=n$
for
$f(n)=n$
for
![]() $1\leq n\leq 15$
. Assume that
$1\leq n\leq 15$
. Assume that
![]() $f(n)=n$
for all
$f(n)=n$
for all
![]() $n\leq N$
. We have
$n\leq N$
. We have
![]() $N\geq 15$
. We show that
$N\geq 15$
. We show that
![]() $f(N+1)=N+1$
. By Theorem 1.2, there exist distinct odious numbers
$f(N+1)=N+1$
. By Theorem 1.2, there exist distinct odious numbers
![]() $x,y$
and z such that
$x,y$
and z such that
![]() $N+1=x+y+z$
where
$N+1=x+y+z$
where
![]() $x,y,z<N$
. Hence, the assumption
$x,y,z<N$
. Hence, the assumption
![]() $f(n)=n$
for all
$f(n)=n$
for all
![]() $n\leq N$
yields
$n\leq N$
yields
![]() $f(N+1)=f(x+y+z)=f(x)+f(y)+f(z)=x+y+z=N+1$
.
$f(N+1)=f(x+y+z)=f(x)+f(y)+f(z)=x+y+z=N+1$
.
Case III:
![]() $k=4$
. By Theorem 1.2 and straightforward calculations, every integer
$k=4$
. By Theorem 1.2 and straightforward calculations, every integer
![]() $\ge 4$
can be written as a sum of four odious numbers.
$\ge 4$
can be written as a sum of four odious numbers.
Note that
![]() $f(4)=4$
,
$f(4)=4$
,
![]() $f(6)=f(2)f(3)=f(2+2+1+1)=2f(2)+2$
and
$f(6)=f(2)f(3)=f(2+2+1+1)=2f(2)+2$
and
![]() $f(12)=4f(3)=f(4+4+2+2)=8+2f(2)$
. For convenience, let
$f(12)=4f(3)=f(4+4+2+2)=8+2f(2)$
. For convenience, let
![]() $a=f(2)$
,
$a=f(2)$
,
![]() $b=f(3)$
. This gives the system of equations
$b=f(3)$
. This gives the system of equations
 $$ \begin{align*} \begin{cases} ab=2a+2\\ 2b=a+4. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} ab=2a+2\\ 2b=a+4. \end{cases} \end{align*} $$
We obtain the two solutions
![]() $f(2)=-2$
,
$f(2)=-2$
,
![]() $f(3)=1$
and
$f(3)=1$
and
![]() $f(2)=2$
,
$f(2)=2$
,
![]() $f(3)=3$
. The first solution yields
$f(3)=3$
. The first solution yields
![]() $f(5)=f(2+1+1+1)=1$
, which leads to the contradiction
$f(5)=f(2+1+1+1)=1$
, which leads to the contradiction
 $$ \begin{align*} f(10)&=f(4+4+1+1)=10\\ &=f(2)f(5)=-2. \end{align*} $$
$$ \begin{align*} f(10)&=f(4+4+1+1)=10\\ &=f(2)f(5)=-2. \end{align*} $$
Thus, we can conclude that
![]() $f(2)=2$
,
$f(2)=2$
,
![]() $f(3)=3$
. So,
$f(3)=3$
. So,
![]() $f(n)=n$
for
$f(n)=n$
for
![]() $n\leq 4$
, and f must be the identity function by induction.
$n\leq 4$
, and f must be the identity function by induction.
Case IV:
![]() $k\geq 5$
. In this case we follow closely Park’s argument in [Reference Park11]. It is clear that the sum of k odious numbers can represent k but cannot represent any number from 1 to
$k\geq 5$
. In this case we follow closely Park’s argument in [Reference Park11]. It is clear that the sum of k odious numbers can represent k but cannot represent any number from 1 to
![]() $k-1$
. Since sums of four odious numbers represent all integers
$k-1$
. Since sums of four odious numbers represent all integers
![]() $\geq 4$
as in Case III, the sum
$\geq 4$
as in Case III, the sum
where
![]() $x,y,z,w\in \mathcal {O}$
, can represent all integers
$x,y,z,w\in \mathcal {O}$
, can represent all integers
![]() $\geq k$
.
$\geq k$
.
Let
![]() $k\geq 5$
. Note that
$k\geq 5$
. Note that
 $$ \begin{align*} (k-2)+8&=(k-2)\cdot1+4+4\\ &=(k-2)\cdot1+7+1,\\ (k-3)+18&=(k-3)\cdot1+14+2+2\\ &=(k-3)\cdot1+7+7+4,\\ (k-4)+33&=(k-4)\cdot1+28+2+2+1\\ &=(k-4)\cdot1+14+14+4+1. \end{align*} $$
$$ \begin{align*} (k-2)+8&=(k-2)\cdot1+4+4\\ &=(k-2)\cdot1+7+1,\\ (k-3)+18&=(k-3)\cdot1+14+2+2\\ &=(k-3)\cdot1+7+7+4,\\ (k-4)+33&=(k-4)\cdot1+28+2+2+1\\ &=(k-4)\cdot1+14+14+4+1. \end{align*} $$
Let
![]() $a=f(2)$
,
$a=f(2)$
,
![]() $b=f(4)$
,
$b=f(4)$
,
![]() $c=f(7)$
. The above equalities give rise to the system of equations
$c=f(7)$
. The above equalities give rise to the system of equations
 $$ \begin{align*} \begin{cases} 2b=c+1\\ ac+2a=2c+b\\ bc+2a=2ac+b. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} 2b=c+1\\ ac+2a=2c+b\\ bc+2a=2ac+b. \end{cases} \end{align*} $$
The solutions are
 $$ \begin{gather*} f(2)=\tfrac{1}{4},\ f(4)=\tfrac{1}{2},\ f(7)=0\\ f(2)=f(4)=f(7)=1\\ f(2)=2,\ f(4)=4,\ f(7)=7. \end{gather*} $$
$$ \begin{gather*} f(2)=\tfrac{1}{4},\ f(4)=\tfrac{1}{2},\ f(7)=0\\ f(2)=f(4)=f(7)=1\\ f(2)=2,\ f(4)=4,\ f(7)=7. \end{gather*} $$
Observe that
![]() $f(k+1)=k-1+f(2)$
,
$f(k+1)=k-1+f(2)$
,
![]() $f(k+4)=k-2+f(4)+f(2)$
and
$f(k+4)=k-2+f(4)+f(2)$
and
![]() $f(k+6)= k-4+f(4)+3f(2)$
.
$f(k+6)= k-4+f(4)+3f(2)$
.
If
![]() $\text {gcd}(4,k+1)=1$
, the equalities
$\text {gcd}(4,k+1)=1$
, the equalities
 $$ \begin{align*} f(4(k+1))=f(\underbrace{4+\cdots4}_{k-3\ \text{times}}+7+7+2)&=f(4)(k-3)+2f(7)+f(2)\\ &=f(4)f(k+1)=f(4)(k-1+f(2)) \end{align*} $$
$$ \begin{align*} f(4(k+1))=f(\underbrace{4+\cdots4}_{k-3\ \text{times}}+7+7+2)&=f(4)(k-3)+2f(7)+f(2)\\ &=f(4)f(k+1)=f(4)(k-1+f(2)) \end{align*} $$
exclude the first set of solutions
![]() $f(2)=\tfrac 14$
,
$f(2)=\tfrac 14$
,
![]() $f(4)=\tfrac 12$
,
$f(4)=\tfrac 12$
,
![]() $f(7)=0$
.
$f(7)=0$
.
If
![]() $4\nmid k+1$
but
$4\nmid k+1$
but
![]() $2 \mid k+1$
, then
$2 \mid k+1$
, then
![]() $\text {gcd}(4,k+4)=1$
, and the equalities
$\text {gcd}(4,k+4)=1$
, and the equalities
 $$ \begin{align*} f(4(k+4))=f(\underbrace{4+\cdots4}_{k-3\ \text{times}}+14+7+7)&=f(4)(k-3)+f(2)f(7)+2f(7)\\ &=f(4)f(k+4)=f(4)(k-2+f(4)+f(2)) \end{align*} $$
$$ \begin{align*} f(4(k+4))=f(\underbrace{4+\cdots4}_{k-3\ \text{times}}+14+7+7)&=f(4)(k-3)+f(2)f(7)+2f(7)\\ &=f(4)f(k+4)=f(4)(k-2+f(4)+f(2)) \end{align*} $$
exclude the first set of solutions.
Finally, if
![]() $4 \mid k+1$
, then
$4 \mid k+1$
, then
![]() $\text {gcd}(4,k+6)=1$
, and we consider
$\text {gcd}(4,k+6)=1$
, and we consider
 $$ \begin{align*} f(4(k+6))=f(\underbrace{4+\cdots4}_{k-3\ \text{times}}+28+7+1)&=f(4)(k-3)+f(4)f(7)+f(7)+1\\ &=f(4)f(k+6)=f(4)(k-4+f(4)+3f(2)), \end{align*} $$
$$ \begin{align*} f(4(k+6))=f(\underbrace{4+\cdots4}_{k-3\ \text{times}}+28+7+1)&=f(4)(k-3)+f(4)f(7)+f(7)+1\\ &=f(4)f(k+6)=f(4)(k-4+f(4)+3f(2)), \end{align*} $$
which excludes the first set of solutions.
Now consider the second solution set
![]() $f(2)=f(4)=f(7)=1$
. Arrange the odious numbers into an increasing sequence, and let
$f(2)=f(4)=f(7)=1$
. Arrange the odious numbers into an increasing sequence, and let
![]() $x_n$
denote the nth term. Then,
$x_n$
denote the nth term. Then,
![]() $f(x_1)=f(x_2)=f(x_3)=f(x_4)=1$
. As seen in Case III, every
$f(x_1)=f(x_2)=f(x_3)=f(x_4)=1$
. As seen in Case III, every
![]() $x_n$
with
$x_n$
with
![]() $n\geq 3$
can be written as a sum of four odious numbers. From the equality
$n\geq 3$
can be written as a sum of four odious numbers. From the equality
we infer that
![]() $f(x_n)=1$
for all
$f(x_n)=1$
for all
![]() $n\geq 5$
inductively. But for sufficiently large n,
$n\geq 5$
inductively. But for sufficiently large n,
![]() $x_n$
can be represented as a sum of k odious numbers by (2.1), so
$x_n$
can be represented as a sum of k odious numbers by (2.1), so
![]() $f(x_n)=k$
, which is a contradiction.
$f(x_n)=k$
, which is a contradiction.
Hence, we conclude that
![]() $f(2)=2$
,
$f(2)=2$
,
![]() $f(4)=4$
and
$f(4)=4$
and
![]() $f(7)=7$
. Moreover, (2.2) yields
$f(7)=7$
. Moreover, (2.2) yields
![]() $f(x_n)=x_n$
for every
$f(x_n)=x_n$
for every
![]() $n\geq 1$
.
$n\geq 1$
.
If N is a sum of k odious numbers, then
![]() $f(N)=N$
. Otherwise, choose an integer
$f(N)=N$
. Otherwise, choose an integer
![]() $M\geq k$
such that
$M\geq k$
such that
![]() $\text {gcd}(M,N)=1$
. Then, M and
$\text {gcd}(M,N)=1$
. Then, M and
![]() $MN$
can be represented as sums of k odious numbers by (2.1). By the multiplicativity of f,
$MN$
can be represented as sums of k odious numbers by (2.1). By the multiplicativity of f,
Therefore,
![]() $f(N)=N$
, and this completes the proof.
$f(N)=N$
, and this completes the proof.
Acknowledgement
The author would like to thank the anonymous referee for helpful suggestions.