Hostname: page-component-7dd5485656-wlg5v Total loading time: 0 Render date: 2025-10-30T13:19:51.407Z Has data issue: false hasContentIssue false
  • English
  • Français

ON NONINNER AUTOMORPHISMS OF SOME FINITE P-GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  08 October 2024

SANDEEP SINGH Open the ORCID record for SANDEEP SINGH [Opens in a new window] ,
ROHIT GARG Open the ORCID record for ROHIT GARG [Opens in a new window]  and
HEMANT KALRA Open the ORCID record for HEMANT KALRA [Opens in a new window]
SANDEEP SINGH
Affiliation:
Department of Mathematics, Akal University, Talwandi Sabo, Punjab 151302, India e-mail: sandeepinsan86@gmail.com
ROHIT GARG
Affiliation:
Department of Mathematics, Government Ripudaman College, Nabha, Punjab 147201, India and School of Mathematical Sciences, National Institute of Science Education and Research, Bhubaneswar, HBNI, P.O. Jatni, Khurda, Odisha 752050, India e-mail: rohitgarg289@gmail.com, rohitgarg289@niser.ac.in
HEMANT KALRA*
Affiliation:
Department of Mathematics, Guru Jambheshwar University of Science and Technology, Hisar, Haryana 125001, India
*
e-mail: happykalra26@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We settle the noninner automorphism conjecture for finite p-groups (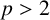$p> 2$) with certain conditions. Also, we give an elementary and short proof of the main result of Ghoraishi [‘On noninner automorphisms of finite nonabelian p-groups’, Bull. Aust. Math. Soc. 89(2) (2014) 202–209].

Keywords

finite p-groupnoninner automorphism

MSC classification

Primary: 20D15: Nilpotent groups, $p$-groups
Secondary: 20D45: Automorphisms

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 3 , June 2025 , pp. 524 - 529
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author is grateful to SERB, Department of Science and Technology, for supporting the research under grant MTR/2022/000331.

References

Abdollahi, A., ‘Finite $p$ -groups of class 2 have noninner automorphisms of order $p$ ’, J. Algebra 312(2) (2007), 876–879.CrossRefGoogle Scholar
Abdollahi, A., ‘Powerful $p$ -groups have non-inner automorphisms of order p and some cohomology’, J. Algebra 323(3) (2010), 779–789.CrossRefGoogle Scholar
Abdollahi, A., Ghoraishi, M. and Wilkens, B., ‘Finite $p$ -groups of class 3 have noninner automorphisms of order $p$ ’, Beitr. Algebra Geom. 54(1) (2013), 363–381.CrossRefGoogle Scholar
Abdollahi, A., Ghoraishi, S. M., Guerboussa, Y., Reguiat, M. and Wilkens, B., ‘Noninner automorphisms of order $p$ for finite $p$ -groups of coclass 2’, J. Group Theory 17(2) (2014) 267–272.CrossRefGoogle Scholar
Deaconescu, M. and Silberberg, G., ‘Noninner automorphisms of order $p$ of finite $p$ -groups’, J. Algebra 250(1) (2002), 283–287.CrossRefGoogle Scholar
Garg, R. and Singh, M., ‘Finite $p$ -groups with non-cyclic center have a non-inner automorphism of order $p$ ’, Arch. Math. (Basel) 117(2) (2021), 129–132.CrossRefGoogle Scholar
Ghoraishi, S. M., ‘A note on automorphisms of finite $p$ -groups’, Bull. Aust. Math. Soc. 87(1) (2013), 24–26.CrossRefGoogle Scholar
Ghoraishi, S. M., ‘On noninner automorphisms of finite nonabelian $p$ -groups’, Bull. Aust. Math. Soc. 89(2) (2014), 202–209.CrossRefGoogle Scholar
Ghoraishi, S. M., ‘On noninner automorphisms of finite p-groups that fix the Frattini subgroup elementwise’, J. Algebra Appl. 17(1) (2018), Article no. 1850137.CrossRefGoogle Scholar
Ghoraishi, S. M., ‘Noninner automorphisms of order $p$ for finite $p$ -groups of restricted coclass’, Arch. Math. (Basel) 117(4) (2021), 361–368.CrossRefGoogle Scholar
Khukhro, E. I. and Mazurov, V. D., Unsolved Problems in Group Theory: The Kourovka Notebook, No. 20, Russian Academy of Sciences, Siberian Branch (Sobolev Institute of Mathematics, Novosibirsk, 2022).Google Scholar
Liebeck, H., ‘Outer automorphisms in nilpotent $p$ -groups of class 2’, J. Lond. Math. Soc. (2) 40(1) (1965), 268–275.CrossRefGoogle Scholar
Rotman, J. J., An Introduction to Homological Algebra, 2nd edn, Universitext (Springer, New York, 2009).CrossRefGoogle Scholar
Ruscitti, M., Legarreta, L. and Yadav, M. K., ‘Non-inner automorphisms of order $p$ in finite $p$ -groups of coclass 3’, Monatsh. Math. 183(4) (2017), 679–697.CrossRefGoogle Scholar
Shabani-Attar, M., ‘Existence of noninner automorphisms of order $p$ in some finite $p$ -groups’, Bull. Aust. Math. Soc. 87(2) (2013), 272–277.CrossRefGoogle Scholar