Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vinh, Le Anh
2011.
On a Furstenberg-Katznelson-Weiss Type Theorem over Finite Fields.
Annals of Combinatorics,
Vol. 15,
Issue. 3,
p.
541.
Shparlinski, Igor E.
2016.
On the additive energy of the distance set in finite fields.
Finite Fields and Their Applications,
Vol. 42,
Issue. ,
p.
187.
Lund, Ben
Pham, Thang
and
Vinh, Le Anh
2018.
Distinct spreads in vector spaces over finite fields.
Discrete Applied Mathematics,
Vol. 239,
Issue. ,
p.
154.
Omar, Mohamed
2025.
Partition Rank and Partition Lattices.
Order,
Vol. 42,
Issue. 2,
p.
371.

 ,
,  and
and 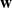 in the
in the 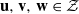 define acute angle triangles. A similar question in the real space ℛ
define acute angle triangles. A similar question in the real space ℛ