Article contents
On the complex complementarity problem
Published online by Cambridge University Press: 17 April 2009
Abstract
The complex linear complementarity problem considered here is the following: Find z such that
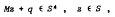
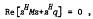
where S is a polyhedral convex cone in Cp, S* the polar cone, M ∈ Cp×p and q ∈ Cp.
Generalizing earlier results in real and complex space, it is shown that if M satisfies RezHMz ≥ 0 for all z ∈ Cp and if the set satisfying Mz + q ∈ S*, z ∈ S is not empty, then a solution to the complex linear complementarity problem exists. If RezHMz > 0 unless z = 0, then a solution to this problem always exists.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1973
References
- 6
- Cited by


