No CrossRef data available.
Article contents
ON THE LIMIT SET OF A COMPLEX HYPERBOLIC TRIANGLE GROUP
Published online by Cambridge University Press: 02 February 2024
Abstract
Let 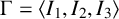 $\Gamma =\langle I_{1}, I_{2}, I_{3}\rangle $ be the complex hyperbolic
$\Gamma =\langle I_{1}, I_{2}, I_{3}\rangle $ be the complex hyperbolic 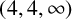 $(4,4,\infty )$ triangle group with
$(4,4,\infty )$ triangle group with 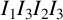 $I_1I_3I_2I_3$ being unipotent. We show that the limit set of
$I_1I_3I_2I_3$ being unipotent. We show that the limit set of 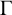 $\Gamma $ is connected and the closure of a countable union of
$\Gamma $ is connected and the closure of a countable union of 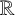 $\mathbb {R}$-circles.
$\mathbb {R}$-circles.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 110 , Issue 2 , October 2024 , pp. 338 - 345
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work was partially supported by the NSFC (Grant No. 12271148).
References
Acosta, M., ‘On the limit set of a spherical CR uniformization’, Algebr. Geom. Topol. 22 (2022), 3305–3325.10.2140/agt.2022.22.3305CrossRefGoogle Scholar
Falbel, E., Guilloux, A. and Will, P., ‘Slim curves, limit sets and spherical CR uniformisations’, Preprint, 2022, arXiv:2205.08797.Google Scholar
Falbel, E. and Parker, J. R., ‘The geometry of the Eisenstein–Picard modular group’, Duke Math. J. 131 (2006), 249–289.10.1215/S0012-7094-06-13123-XCrossRefGoogle Scholar
Falbel, E. and Zocca, V., ‘A Poincaré’s polyhedron theorem for complex hyperbolic geometry’, J. reine angew. Math. 516 (1999), 133–158.10.1515/crll.1999.082CrossRefGoogle Scholar
Goldman, W. M., Complex Hyperbolic Geometry, Oxford Mathematical Monographs (Oxford University Press, Oxford, 1999).10.1093/oso/9780198537939.001.0001CrossRefGoogle Scholar
Jiang, Y., Wang, J. and Xie, B., ‘A uniformizable spherical CR structure on a two-cusped hyperbolic 3-manifold’, Algebr. Geom. Topol. 23 (2023), 4143–4184.10.2140/agt.2023.23.4143CrossRefGoogle Scholar
Parker, J. R., Notes on Complex Hyperbolic Geometry (University of Durham, Durham, 2003). https://maths.dur.ac.uk/users/j.r.parker/img/NCHG.pdf.Google Scholar
Pratoussevitch, A., ‘Traces in complex hyperbolic triangle groups’, Geom. Dedicata 111 (2005), 159–185.10.1007/s10711-004-1493-0CrossRefGoogle Scholar
Schwartz, R. E., ‘Complex hyperbolic triangle groups’, in: Proceedings of the International Congress of Mathematicians, Beijing, 2002, Volume II: Invited Lectures (ed. Li, T.) (Higher Education Press, Beijing, 2002), 339–350.Google Scholar
Schwartz, R. E., ‘Real hyperbolic on the outside, complex hyperbolic on the inside’, Invent. Math. 151 (2003), 221–295.10.1007/s00222-002-0245-8CrossRefGoogle Scholar
Takeuchi, K., ‘Arithmetic triangle groups’, J. Math. Soc. Japan 29 (1977), 91–106.10.2969/jmsj/02910091CrossRefGoogle Scholar


