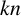1. Introduction
The distribution of the differences of primes is a recurring theme in number theory. It is generally believed that every even number is the difference of two primes.
Definition 1.1 (Maillet number, Kronecker number)
An even number n is called a Maillet number if it can be written as the difference of two primes and a Kronecker number if it can be written in infinitely many ways as the difference of two primes.
For a given positive even number, we can check directly if it is a Maillet number by finding a pair of primes. However, no concrete Kronecker number is known. Whether
$2$
is a Kronecker number is the well-known twin prime conjecture.
Conjecture 1.2 (Kronecker [Reference Kronecker11])
Every even number can be written in infinitely many ways as the difference of two primes.
This conjecture is currently out of reach. However, recent breakthroughs towards the twin prime conjecture indicate that there is a Kronecker number not exceeding 246 (see [Reference Goldston, Pintz and Yildirim2, Reference Maynard12, Reference Polymath14, Reference Zhang15]).
Let
$\mathcal {K}$
be the set of all Kronecker numbers. We investigate how ‘large’ this set might be. A set
$S\subset \mathbb {N}$
is called syndetic if there exists an integer k such that
$\{a+1, a+2,\ldots , a+k\}\cap S\neq \emptyset $
for any
$a\in \mathbb {N}$
. Pintz [Reference Pintz, Sander, Steuding and Steuding13] proved that
$\mathcal {K}$
is a syndetic set and Granville et al. [Reference Granville, Kane, Koukoulopoulos, Lemke Oliver, Pomerance and Rassias4] gave a different proof. Unfortunately, the integer k is not determined effectively in [Reference Granville, Kane, Koukoulopoulos, Lemke Oliver, Pomerance and Rassias4, Reference Pintz, Sander, Steuding and Steuding13].
Definition 1.3 (
$\Delta _r$
-set and
$\Delta _r^*$
-set)
Let r be a given positive integer.
-
• A
$\Delta _r$
-set is a difference set of a set
$S\subset \mathbb {N}$
with
$|S|\ge r$
, that is,
$$ \begin{align*} \Delta(S)=(S-S)\cap\mathbb{N}=\{a-b: a, b\in S, a>b\}. \end{align*} $$
-
• A set
$S\subset \mathbb {N}$
is a
$\Delta _r^*$
-set if the intersection of S with any
$\Delta _r$
-set is not empty.
Clearly, every
$\Delta _r^*$
-set is syndetic.
Theorem 1.4 (Huang and Wu [Reference Huang and Wu10])
$\mathcal {K}$
is a
$\Delta _r^*$
-set for any
$r\ge 721$
.
It is also mentioned in [Reference Huang and Wu10] that the number
$721$
can be sharpened to
$19$
if the primes have level of distribution
$\theta $
for every
$\theta <1$
. Given
$\theta>0$
, we say the primes have ‘level of distribution
$\theta $
’ if, for any
$W>0$
,
$$ \begin{align*} \sum_{q\le x^\theta}\max_{(a,q)=1}\bigg|\pi(x;q,a)-\frac{\pi(x)}{\phi(q)}\bigg|\ll_W\frac{x}{(\log x)^W}. \end{align*} $$
The numerical bound for r in Theorem 1.4 gives an effective lower bound for the density
$\alpha $
of
$\mathcal {K}$
among even numbers. As shown in the Appendix, one may deduce from Theorem 1.4 that
$$ \begin{align*} \alpha\ge\frac 1{360}\prod_{p\le 720}\bigg(1-\frac{1}{p}\bigg). \end{align*} $$
We try to obtain more information on how large
$\mathcal {K}$
is by studying the division and multiplication of Kronecker numbers. Our first result about the representation of integers by products of differences of primes is motivated by the following question.
Question 1.5 (Fish [Reference Fish1])
For a given infinite set
$E\subset \mathbb {Z}$
, how much structure does the set
$(E-E)\cdot (E-E)$
possess?
Fish [Reference Fish1] considered the question when E is a subset of
$\mathbb {Z}$
of positive density. Using Furstenberg’s correspondence principle, he proved that there exist
$k_0$
(depending on the densities of
$E_1$
and
$E_2$
) and
$k\le k_0$
such that
$$ \begin{align*} k\mathbb{Z}\subset(E_1-E_1)\cdot(E_2-E_2). \end{align*} $$
It is natural to consider the question when E is the set of primes. This case is not covered by Fish’s work since the set of primes is an infinite set of
$\mathbb {Z}$
but does not have positive upper Banach density. In [Reference Goswami3], Goswami used Theorem 1.4 to extend Fish’s result to the case of primes, showing that
$$ \begin{align} k\mathbb{Z}\subset(\mathbb{P}-\mathbb{P})\cdot(\mathbb{P}-\mathbb{P}). \end{align} $$
We can say more. On the right-hand side of (1.1), one factor can be restricted to a finite subset of
$\mathbb {P}-\mathbb {P}$
, consisting of 720 Maillet numbers, while the other factor takes values among Kronecker numbers.
Theorem 1.6. There exist a computable constant k and a set D, consisting of at most 720 computable Maillet numbers, such that
$k\mathbb {Z}\subset D\cdot \mathcal {K}$
.
The proof of Theorem 1.6 is based on Theorem 1.4 as well as recent work on linear equations in primes by Green et al. [Reference Green, Tao and Ziegler7]. The number
$720$
could be sharpened to
$18$
if the primes have level of distribution
$\theta $
for every
$\theta <1$
.
Seeking further evidence on the size of
$\mathcal {K}$
, we also consider the ratio of two Kronecker numbers and prove the following result.
Theorem 1.7. Every positive rational number can be written as a ratio of two elements from
$\mathcal {K}.$
2. Representation of integers
In this section, we give the proof of Theorem 1.6.
2.1. Linear equations in primes
We outline some of the work of Green and Tao on linear equations in primes. More details can be found in [Reference Green and Tao5]. Let
$d,t$
be integers. A system of affine-linear forms on
$\mathbb {Z}^d$
is a collection
$\Psi =\{\psi _1,\dots ,\psi _t\}$
with
$\psi _i: \mathbb {Z}^d\rightarrow \mathbb {Z}$
being affine-linear forms. If
$N>0$
, the size
$\| \Psi \|_N$
of
$\Psi $
relative to the scale N is
$$ \begin{align*} \|\Psi\|_N:=\sum_{i=1}^t\sum_{j=1}^d|\dot{\psi}_i(e_j)|+\sum_{i=1}^t\bigg|\frac{\psi_i(0)}{N}\bigg|, \end{align*} $$
where
$$ \begin{align*} \dot{\psi}_i(e_j)=\psi_i(e_j)-\psi_i(0) \end{align*} $$
with
$e_1, e_2, \dots , e_d$
being the standard basis for
$\mathbb {Z}^d$
. For a system
$\Psi $
, its local factor
$\beta _p$
for a prime p is
$$ \begin{align} \beta_p:=\frac1{p^d}\sum_{n\in\mathbb{Z}_p^d}\prod_{i=1}^t\Lambda_{\mathbb{Z}_p}(\psi_i(n)), \end{align} $$
where
$\mathbb {Z}_p=\{0,1,\dots ,p-1\}$
is the set of residue classes of integers modulo p and
$\Lambda _{\mathbb {Z}_p}(n)$
is the local von Mangoldt function defined by
$$ \begin{align*} \Lambda_{\mathbb{Z}_p}(n)=\begin{cases} \dfrac{p}{p-1} & \text{if}\ (n,p)=1 \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
For a convex body
$K\subset [-N,N]^d$
, the archimedean factor is
$$ \begin{align*} \beta_\infty:=\text{vol}_d(K\cap\Psi^{-1}(\mathbb{R}^+)^t). \end{align*} $$
Definition 2.1 (Complexity)
The complexity of
$\Psi $
is the least integer s such that, for each
$\psi _i$
, one can partition the remaining
$t-1$
forms
$\{\psi _j:j\neq i\}$
into
$s+1$
groups, such that
$\psi _i$
does not lie in the affine-linear span of any group; if no such s exists, we say that the complexity is
$\infty $
(see [Reference Green and Tao5, Definition 1.5]).
The main results of [Reference Green and Tao5–Reference Green, Tao and Ziegler7] can be summarised as follows.
Theorem 2.2 (Green, Tao and Ziegler)
Let
$N, d, t, L$
be positive integers and let
$\Psi =\{\psi _1, \dots , \psi _t\}$
be a system of affine-linear forms with size
$\| \Psi \|_N\le L$
. Let
$K\subset [-N,N]^d$
be a convex body. If
$\Psi $
has finite complexity, then
$$ \begin{align*} \#\{n\in K\cap\mathbb{Z}^d: \psi_1(n), \dots, \psi_t(n) \ \ \text{prime}\}=(1+o_{t,d,L}(1))\frac{\beta_\infty}{\log^tN}\prod_{p}\beta_{p}+o_{t,d,L}\bigg(\frac{N^d}{\log^tN}\bigg), \end{align*} $$
where
$\beta _\infty $
is typically of size
$N^d$
and the singular product
$\prod _{p}\beta _{p}$
is always convergent.
Theorem 2.2 was first proved by Green and Tao assuming that the inverse Gowers-norm conjecture and the Möbius and nilsequences conjecture are true (see [Reference Green and Tao5, Main Theorem]). These two conjectures were already known for the case
$s\le 2$
(see [Reference Green and Tao5, Corollary 1.7]). In their following papers, they proved the Möbius and nilsequences conjecture for any s (see [Reference Green and Tao6, Main Theorem]) and, in combination with Ziegler, proved the inverse Gowers-norm conjecture (see [Reference Green, Tao and Ziegler7, Theorem 1.3]).
It was pointed out in [Reference Green and Tao5] that the singular product
$\prod _{p}\beta _{p}$
is always convergent, but it may still vanish since
$\beta _p=0$
is possible for small p. So, the theorem only works for a system of affine-linear forms with
$\beta _p\neq 0$
, for all p. (It is enough to consider small
$p=O_{t,d,L}(1)$
here.)
2.2. Proof of Theorem 1.6
To prove our theorem, we will appeal to a special case of Theorem 2.2, which we provide in the following lemma.
Lemma 2.3. Let
$\Psi =\{\psi _1,\dots ,\psi _t\}$
be a system of affine-linear forms of finite complexity with
$\psi _i: \mathbb {Z^+}^d\rightarrow \mathbb {Z^+}$
,
$1\le i\le t$
, and
$\beta _p\neq 0$
for any prime p. Then there are infinitely many lattice points
$n\in {\mathbb {Z}^+}^d$
, which make all
$\psi _i(n)$
prime.
Proof. In Theorem 2.2, we can take
$K=[-N,N]^d$
. For
$\psi _i: \mathbb {Z^+}^d\rightarrow \mathbb {Z^+}$
,
$$ \begin{align*} \beta_\infty:=\text{vol}_d(K\cap\Psi^{-1}((\mathbb{R}^+)^t)\ge \text{vol}_d([-N,N]^d\cap{\mathbb{Z}^+}^d)\ge N^d. \end{align*} $$
Also, the singular product
$\prod _{p}\beta _{p}$
does not vanish since
$\beta _p\neq 0$
for all p. Thus, the asymptotic formula in Theorem 2.2 has a dominant main term, and the lemma follows immediately.
For
$j=1,2,\dots ,720$
, we define
$a_j={720!}/{j}$
. We consider the system of affine-linear forms
$\Psi =\{\psi _1, \dots , \psi _{1440}\}$
defined by
$$ \begin{align*} \psi_{2j-1}(n_1,\dots,n_{720},m) & =n_j,\notag\\ \psi_{2j}(n_1,\dots,n_{720},m) & =n_j+a_jm, \notag \end{align*} $$
for
$j=1,\dots ,720$
. Note that each form
$\psi _i\in \Psi $
lies in the affine span of all the other forms, but we can partition the remaining forms into two groups, such that
$\psi _i$
does not lie in the affine span of either group. For example, for
$i=2j-1$
, we may take
$\psi _{2j}$
as one group and the rest as the other group, and for
$i=2j$
, we take
$\psi _{2j-1}$
as one group and the rest as the other group. Thus,
$\Psi $
is a special system of affine-linear forms with complexity
$s=1$
. It is obvious that
$\psi _i: \mathbb {Z^+}^d\rightarrow \mathbb {Z^+}$
since all coefficients are positive integers.
To apply Lemma 2.3, we also need
$\beta _p\neq 0$
. By (2.1), this is the case if, for each p, we can find a lattice point
$n\in \mathbb {Z}_p^d$
such that
$(\psi _i(n),p)=1$
for all i. Obviously, the lattice point
$n=(1,1,\ldots ,1,0)\in \mathbb {Z}_p^{721}$
has this property. Thus, by Lemma 2.3, there are infinitely many lattice points
$(n_1,\ldots , n_{720}, m)\in {\mathbb {Z}^+}^{721}$
, which make all
$\psi _i$
prime. That is to say, for each m in this set of lattice points, the set
$\{a_1m, a_2m, \dots , a_{720}m\}$
consists of Maillet numbers. We choose
$m'$
as the least one of these m; it is a computable number since the system of affine-linear forms is specific.
To prove the theorem, we take the constant
$k=720!m'$
and the set to be
$$ \begin{align*} D=\{a_1 m', a_2 m', \dots, a_{720} m'\}. \end{align*} $$
For any integer
$b>0$
, Theorem 1.4 shows that there is at least one Kronecker number in the set
$\{b, 2b, \dots , 720b\}$
. If
$jb$
with
$1\le j\le 720$
is a Kronecker number, then
$$ \begin{align*} kb=a_j m'\cdot j b\in D \cdot \mathcal{K}, \end{align*} $$
which establishes Theorem 1.6.
3. Representation of rationals
In this section, we will use arguments from Ramsey theory to prove Theorem 1.7. First we will prove three lemmas and then a more general Theorem 3.6 which implies Theorem 1.7 as a corollary. The lemmas are standard and can be found in [Reference Hindman and Strauss9]. We include the short proofs for the sake of completeness.
The notions of IP sets and
${IP}_r$
sets are well studied in Ramsey theory (see [Reference Hindman and Strauss9]). Let
$\mathcal {P}_{f}(\mathbb {N})$
denote the collection of nonempty finite subsets of
$\mathbb {N}.$
Definition 3.1. A set
$A\subset \mathbb {N}$
is said to be an IP set if there exists a sequence
$\langle x_n \rangle _{n\in \mathbb {N}}$
such that
$A={FS}(\langle x_n \rangle _{n\in \mathbb {N}}) = \{\sum _{t\in H} x_t : H\in \mathcal {P}_f(\mathbb {N})\}$
. Similarly, a set
$A\subset \mathbb {N}$
is said to be an
${IP}_r$
set for some
$r\in \mathbb {N}$
if there exists a sequence
$\langle x_n \rangle _{n=1}^r$
such that
$A={FS}(\langle x_n \rangle _{n=1}^r)$
.
A set is said to be an
${IP}^{\star }$
set if it intersects every IP set and an
${IP}_r^{\star }$
set if it intersects every
${IP}_r$
set. Note that every
${IP}_{r}$
set contains a
$\Delta _{r}$
set. To check this, let
${FS}(\langle x_{n}\rangle _{n=1}^{r})$
be an
$IP_{r}$
set and let
$$ \begin{align*} S=\{ x_{1},x_{1}+x_{2},\ldots,x_{1}+x_{2}+\cdots+x_{n}\}. \end{align*} $$
Then
$FS(\langle x_{n}\rangle _{n=1}^{r})$
contains all elements of the form
$\{ s-t:s>t\text { and }s,t\in S\} $
. Hence, every
$\Delta _{r}^{\star }$
set is
$IP_{r}^{\star }$
. Again, every IP set contains an
${IP}_r$
set for some
$r\in \mathbb {N}$
and hence every
${IP}_r^{\star }$
set is
${IP}^{\star }$
. In particular,
$\mathcal {K}$
is
${IP}_{721}^{\star }$
and hence an
${IP}^{\star }$
set.
A sub-IP set of
${FS}(\langle x_{n}\rangle _{n\in \mathbb {N}})$
is a set of the form
${FS}(\langle y_{n}\rangle _{n\in \mathbb {N}})\subseteq {FS}(\langle x_{n}\rangle _{n\in \mathbb {N}})$
, where
$y_t=\sum _{s\in H_t}x_s$
for each
$t\in \mathbb {N}$
and
$(H_i)_{i\in \mathbb {N}}$
is a sequence in
$\mathcal {P}_{f}(\mathbb {N})$
such that
$H_i\cap H_j = \emptyset $
for each
$i\neq j$
.
The following lemma is a direct corollary of Hindman’s theorem [Reference Hindman8]. Here, ‘colouring’ means a disjoint partition and a set is ‘monochromatic’ if it lies in one part of the partition.
Lemma 3.2. For every finite colouring of an IP set, there exists a monochromatic sub-IP set.
The next lemma says that dilation of an
${IP}^{\star }$
set by a number is again an
${IP}^{\star }$
set.
Lemma 3.3. Let
$A\subseteq \mathbb {N}$
be an
${IP}^{\star }$
set. Then for any
$m\in \mathbb {N}$
,
$m\cdot A=\lbrace mx:x\in A\rbrace $
is again an
${IP}^{\star }$
set.
Proof. Let
$\langle x_{n}\rangle _{n\in \mathbb {N}}$
be any sequence and for each
$i\in \mathbb {N}$
, let
$x_{i}\equiv j(i)\ \mod m$
, where
$j(i)\in \{ 0,1,\ldots ,m-1\} .$
As
$\mathbb {Z}_m$
is finite, there exists
$k\in \{ 0,1,\ldots ,m-1\}$
and an infinite sequence
$(n_i)_{i\in \mathbb {N}}$
such that
$x_{n_i}\equiv k\ \mod m.$
Let
$H_1$
be a set of m terms from the sequence
$(n_i)$
so that
$m\mid \sum _{t\in H_{1}}x_{t}$
. Continue to choose further sets of terms in this way to obtain disjoint finite subsets of
$H_n$
of
$\mathbb {N}$
such that
$m\mid \sum _{t\in H_{n}}x_{t}$
for each
$n\in \mathbb {N}$
. Choose a new sequence
$\langle y_{n}\rangle _{n\in \mathbb {N}}$
such that
$y_{n}=\sum _{t\in H_{n}}x_{t}/m$
for each
$n\in \mathbb {N}$
. Then
$A\cap {FS}(\langle y_{n}\rangle _{n\in \mathbb {N}})\neq \emptyset $
and this implies
$m\cdot A\cap {FS}(\langle x_{n}\rangle _{n\in \mathbb {N}})\neq \emptyset $
, finishing the proof.
The next lemma says that any
${IP}^{\star }$
set contains an IP set. In fact, it contains a sub-IP set of any given IP set.
Lemma 3.4. Let
${FS}(\langle x_n \rangle _{n\in \mathbb {N}})$
be any IP set and let A be any
${IP}^{\star }$
set. Then there exists a sub-IP set
${FS}(\langle y_n \rangle _{n\in \mathbb {N}})$
of
${FS}(\langle x_n \rangle _{n\in \mathbb {N}})$
such that A contains
${FS}(\langle y_n \rangle _{n\in \mathbb {N}})$
.
Proof. Partition
${FS}(\langle x_n \rangle _{n\in \mathbb {N}})$
by
$$ \begin{align*}{FS}(\langle x_n \rangle_{n\in \mathbb{N}})=(A\cap {FS}(\langle x_n \rangle_{n\in \mathbb{N}})) \cup ( {FS}(\langle x_n \rangle_{n\in \mathbb{N}})\setminus A).\end{align*} $$
From Lemma 3.2, there is a sub-IP set
${FS}(\langle y_n \rangle _{n\in \mathbb {N}}))\subseteq {FS}(\langle x_n \rangle _{n\in \mathbb {N}}))$
such that either
${FS}(\langle y_n \rangle _{n\in \mathbb {N}}))\subseteq A\cap {FS}(\langle x_n \rangle _{n\in \mathbb {N}})$
or
${FS}(\langle y_n \rangle _{n\in \mathbb {N}}))\subseteq {FS}(\langle x_n \rangle _{n\in \mathbb {N}})\setminus A.$
Since A is an
${IP}^{\star }$
set,
${FS}(\langle y_n \rangle _{n\in \mathbb {N}}))\cap A$
must be nonempty. This immediately implies that the second case is not possible. So,
${FS}(\langle y_n \rangle _{n\in \mathbb {N}}))\subseteq A$
and the lemma follows.
The next lemma is the final ingredient for our proof.
Lemma 3.5. The intersection of finitely many
${IP}^{\star }$
sets is again an
${IP}^{\star }$
set.
Proof. Let
$A_1,A_2,\ldots ,A_n$
be
${IP}^{\star }$
sets and let
${FS}(\langle x_n \rangle _{n\in \mathbb {N}})$
be any IP set. From Lemma 3.4, there is a sub-
$IP$
set
${FS}(\langle y_n \rangle _{n\in \mathbb {N}}))\subseteq A_1\cap {FS}(\langle x_n \rangle _{n\in \mathbb {N}})$
and so
${FS}(\langle y_n \rangle _{n\in \mathbb {N}}))\subseteq A_1.$
Applying Lemma 3.4 again gives a sub-IP set
${FS}(\langle z_n \rangle _{n\in \mathbb {N}}))\subseteq A_2\cap {FS}(\langle y_n \rangle _{n\in \mathbb {N}})$
and so
${FS}(\langle z_n \rangle _{n\in \mathbb {N}}))\subseteq A_2.$
Hence,
${FS}(\langle z_n \rangle _{n\in \mathbb {N}}))\subseteq A_1\cap A_2.$
Iterating this argument produces a sub-
$IP$
set
${FS}(\langle a_n \rangle _{n\in \mathbb {N}})$
of
${FS}(\langle x_n \rangle _{n\in \mathbb {N}})$
such that
${FS}(\langle a_n \rangle _{n\in \mathbb {N}})\subseteq A_1\cap A_2\cap \cdots \cap A_n.$
As
${FS}(\langle x_n \rangle _{n\in \mathbb {N}})$
is any
$IP$
set, arbitrarily chosen,
$A_1\cap A_2\cap \cdots \cap A_n$
is an
${IP}^{\star }$
set. This completes the proof.
The following theorem is an abstract formulation which strengthens Theorem 1.7.
Theorem 3.6. If A is any
${IP}^{\star }$
set and B is an
$IP$
set, then
$$ \begin{align*}\mathbb{Q}_{>0}=\frac{A}{B}=\bigg\lbrace \frac{a}{b}:a\in A, b\in B \bigg\rbrace.\end{align*} $$
Proof. Let
${m}/{n}\in \mathbb {Q}_{>0}.$
Now
$m\cdot B$
is an IP set and, from Lemma 3.3,
$n\cdot A$
is an
${IP}^{\star }$
set. Hence,
$n\cdot A \cap m\cdot B \neq \emptyset .$
Let
$x=na=mb$
, where
$a\in A, b\in B.$
Then
$m/n=a/b\in A/B.$
This completes the proof.
Proof of Theorem 1.7
As
$\mathcal {K}$
is an
${IP}_{721}^{\star }$
set, it is an
${IP}^{\star }$
set. Again, by Lemma 3.4,
$\mathcal {K}$
contains an IP set. So the desired result follows from Theorem 3.6.
The proof of Theorem 1.7 gives the following more powerful result.
Corollary 3.7. For any
$IP$
set
$\mathcal {D}\subset \mathcal {K}$
, we have
$\mathbb {Q}_{>0}={\mathcal {K}}/{\mathcal {D}}$
and hence also
$\mathbb {Q}_{>0}={\mathcal {D}}/{\mathcal {K}}$
.
Acknowledgment
The authors are very grateful to the referee for a careful reading of the manuscript and pointing out some imprecisions in the initial version.
Appendix. The density of Kronecker numbers
In this section, we provide a simple proof for
$$ \begin{align} \alpha\ge\frac 1{360}\prod_{p\le 720}\bigg(1-\frac{1}{p}\bigg) \end{align} $$
by providing a lower bound for the density of a general
$\Delta _r^*$
-set. With
$S=\{a,2a,\dots ,r a\}$
in the definition of
$\Delta _r^*$
-set, the following fact is obvious.
Lemma A.1. Let H be a
$\Delta _r^*$
-set and
$A_r(a)=\{a,2a,\dots ,(r-1)a\}$
. Then,
$H\cap A_r(a)\neq \emptyset $
for any integer
$a>0$
,
Theorem A.2. If H is a
$\Delta _r^*$
-set, then
$$ \begin{align*} \frac{|H\cap[1,N]|}{N}\ge \prod_{p\le r-1}\bigg(1-\frac{1}{p}\bigg)+o(1). \end{align*} $$
Proof. By Lemma A.1, every
$A_r(a)$
contains at least one element of H. We obtain a lower bound for the cardinality of H by counting the number of the sets
$A_r(a)$
which are mutually disjoint. If
$a<b$
are two integers with
$A_r(a)\cap A_r(b)\neq \emptyset $
, then there are integers
$i,j$
with
$(i,j)=1$
and
$1\le i<j\le r-1$
such that
$a/b = i/j$
. The sets
$A_r(a)$
where a is not divisible by any prime less than
$r-1$
are therefore mutually disjoint. For sufficiently large N,
$$ \begin{align*} \bigg|\bigg\{a: \bigg(a,\prod_{p\le r-1}p\bigg)=1, A_r(a)\subset [1,N]\bigg\}\bigg|=\frac N{r}\prod_{p\le r-1}\bigg(1-\frac{1}{p}\bigg)+O(1). \end{align*} $$
The theorem follows immediately.
Finally, (A.1) follows immediately from Theorems 1.4 and A.2 by taking
$r=721$
.
