Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T15:46:56.946Z Has data issue: false hasContentIssue false
  • English
  • Français

A PRIME ESSENTIAL RING THAT GENERATES A SPECIAL ATOM

Part of: Radicals and radical properties of rings

Published online by Cambridge University Press:  02 November 2016

SRI WAHYUNI ,
INDAH EMILIA WIJAYANTI  and
HALINA FRANCE-JACKSON
SRI WAHYUNI
Affiliation:
Jurusan Matematika, FMIPA UGM, Sekip Utara, Yogyakarta, Indonesia email swahyuni@ugm.ac.id
INDAH EMILIA WIJAYANTI
Affiliation:
Jurusan Matematika, FMIPA UGM, Sekip Utara, Yogyakarta, Indonesia email ind_wijayanti@ugm.ac.id
HALINA FRANCE-JACKSON*
Affiliation:
Department of Mathematics and Applied Mathematics, Summerstrand Campus (South), PO Box 77000, Nelson Mandela Metropolitan University, Port Elizabeth 6031, South Africa email main@easterncape.co.uk
*
✉ main@easterncape.co.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

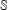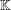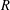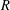A special atom (respectively, supernilpotent atom) is a minimal element of the lattice $\mathbb{S}$ of all special radicals (respectively, a minimal element of the lattice $\mathbb{K}$ of all supernilpotent radicals). A semiprime ring $R$ is called prime essential if every nonzero prime ideal of $R$ has a nonzero intersection with each nonzero two-sided ideal of 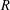$R$ . 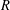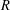We construct a prime essential ring $R$ such that the smallest supernilpotent radical containing $R$ is not a supernilpotent atom but where the smallest special radical containing 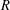$R$ is a special atom. This answers a question put by Puczylowski and Roszkowska.

Keywords

prime essential ringprime radicalspecial and supernilpotent radicalsspecial and supernilpotent atomsleft hereditary radical

MSC classification

Primary: 16N80: General radicals and rings
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 2 , April 2017 , pp. 214 - 218
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Andrunakievich, V. A. and Ryabukhin, Yu. M., Radicals of Algebra and Structure Theory (Nauka, Moscow, 1979) (in Russian).Google Scholar
France-Jackson, H., ‘∗-rings and their radicals’, Quaes. Math. 8 (1985), 231–239.Google Scholar
France-Jackson, H., ‘On atoms of the lattice of supernilpotent radicals’, Quaes. Math. 10 (1987), 251–256.CrossRefGoogle Scholar
France-Jackson, H., ‘On rings generating atoms of lattices of supernilpotent and special radicals’, Bull. Aust. Math. Soc. 44 (1991), 203–205.CrossRefGoogle Scholar
France-Jackson, H., ‘On prime essential rings’, Bull. Aust. Math. Soc. 47 (1993), 287–290.CrossRefGoogle Scholar
France-Jackson, H., ‘On special atoms’, J. Aust. Math. Soc. (Series A) 64 (1998), 302–306.Google Scholar
France-Jackson, H., ‘Rings related to special atoms’, Quaes. Math. 24 (2001), 105–109.CrossRefGoogle Scholar
France-Jackson, H., ‘On left (right) strong and left (right) hereditary radicals’, Quaes. Math. 29 (2006), 329–334.Google Scholar
France-Jackson, H. and Leavitt, W. G., ‘On 𝛽-classes’, Acta Math. Hungar. 90(3) (2001), 243–252.CrossRefGoogle Scholar
Gardner, B. J., ‘Some recent results and open problems concerning special radicals’, in: Radical Theory: Proceedings of the 1988 Sendai Conference (ed. Kyuno, S.) (Uchida Rokakuho Pub. Co., Tokyo, 1989), 25–56.Google Scholar
Gardner, B. J. and Stewart, P. N., ‘Prime essential rings’, Proc. Edinb. Math. Soc. (2) 34 (1991), 241–250.Google Scholar
Gardner, B. J. and Wiegandt, R., Radical Theory of Rings (Marcel Dekker Inc., New York, 2004).Google Scholar
Korolczuk, H., ‘A note on the lattice of special radicals’, Bull. Polish Acad. Sci. Math. 29 (1981), 103–104.Google Scholar
Puczylowski, E. R. and Roszkowska, E., ‘Atoms of lattices of associative rings’, in: Radical Theory: Proceedings of the 1988 Sendai Conference (ed. Kyuno, S.) (Uchida Rokakuho Pub. Co., Tokyo, 1989), 123–134.Google Scholar
Snider, R. L., ‘Lattices of radicals’, Pacific J. Math. 40 (1972), 207–220.CrossRefGoogle Scholar