Article contents
PROOF OF A CONJECTURE OF BANERJEE AND DASTIDAR ON ODD CRANK
Published online by Cambridge University Press: 13 January 2023
Abstract
Recently, when studying intricate connections between Ramanujan’s theta functions and a class of partition functions, Banerjee and Dastidar [‘Ramanujan’s theta functions and parity of parts and cranks of partitions’, Ann. Comb., to appear] studied some arithmetic properties for 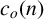 $c_o(n)$, the number of partitions of n with odd crank. They conjectured a congruence modulo
$c_o(n)$, the number of partitions of n with odd crank. They conjectured a congruence modulo 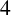 $4$ satisfied by
$4$ satisfied by 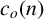 $c_o(n)$. We confirm the conjecture and evaluate
$c_o(n)$. We confirm the conjecture and evaluate 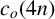 $c_o(4n)$ modulo
$c_o(4n)$ modulo 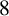 $8$ by dissecting some q-series into even powers. Moreover, we give a conjecture on the density of divisibility of odd cranks modulo 4, 8 and 16.
$8$ by dissecting some q-series into even powers. Moreover, we give a conjecture on the density of divisibility of odd cranks modulo 4, 8 and 16.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 108 , Issue 3 , December 2023 , pp. 406 - 411
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work was partially supported by the National Natural Science Foundation of China (No. 12201093), the Natural Science Foundation Project of Chongqing CSTB (No. CSTB2022NSCQ–MSX0387), the Science and Technology Research Program of Chongqing Municipal Education Commission (No. KJQN202200509) and the Doctoral start-up research grant (No. 21XLB038) of Chongqing Normal University.
References
- 3
- Cited by


