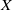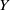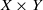Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Di Maio, Giuseppe
and
Kočinac, Ljubiša D.R.
2015.
A note on quasi-Menger and similar spaces.
Topology and its Applications,
Vol. 179,
Issue. ,
p.
148.
Kočinac, Ljubiša D.R.
2020.
Variations of classical selection principles: An overview.
Quaestiones Mathematicae,
Vol. 43,
Issue. 8,
p.
1121.