Let p be a complex polynomial, of the form 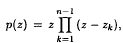 , where |zk| ≥ 1 when 1 ≤ k ≤ n − 1. Then p′(z) ≠ 0 if |z| /n.
, where |zk| ≥ 1 when 1 ≤ k ≤ n − 1. Then p′(z) ≠ 0 if |z| /n.
Let B(z, r) denote the open ball in 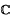 with centre z and radius r, and
with centre z and radius r, and 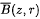 denote its closure. The Gauss-Lucas theorem states that every critical point of a complex polynomial p of degree at least 2 lies in the convex hull of its zeros. This theorem has been further investigated and developed. B. Sendov conjectured that, if all the zeros of p lie in
denote its closure. The Gauss-Lucas theorem states that every critical point of a complex polynomial p of degree at least 2 lies in the convex hull of its zeros. This theorem has been further investigated and developed. B. Sendov conjectured that, if all the zeros of p lie in 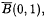 then, for any zero ζ of p, the disc
then, for any zero ζ of p, the disc 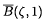 contains at least one zero of p′; see [3, Problem 4.1]. This conjecture has attracted much attention-see, for example, [1], and the papers cited there. In connection with this conjecture, Brown [2] posed the following problem.
contains at least one zero of p′; see [3, Problem 4.1]. This conjecture has attracted much attention-see, for example, [1], and the papers cited there. In connection with this conjecture, Brown [2] posed the following problem.