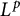 $L^p$-regularity of the Bergman projection on quotient domains
$L^p$-regularity of the Bergman projection on quotient domainsPublished online by Cambridge University Press: 08 February 2021
We obtain sharp ranges of 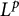 $L^p$
-boundedness for domains in a wide class of Reinhardt domains representable as sublevel sets of monomials, by expressing them as quotients of simpler domains. We prove a general transformation law relating
$L^p$
-boundedness for domains in a wide class of Reinhardt domains representable as sublevel sets of monomials, by expressing them as quotients of simpler domains. We prove a general transformation law relating 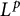 $L^p$
-boundedness on a domain and its quotient by a finite group. The range of p for which the Bergman projection is
$L^p$
-boundedness on a domain and its quotient by a finite group. The range of p for which the Bergman projection is 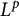 $L^p$
-bounded on our class of Reinhardt domains is found to shrink as the complexity of the domain increases .
$L^p$
-bounded on our class of Reinhardt domains is found to shrink as the complexity of the domain increases .
Chase Bender was supported by a Student Research and Creative Endeavors grant from Central Michigan University.
Debraj Chakrabarti was partially supported by National Science Foundation grant DMS-1600371.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
 $L^p$
-regularity of the Bergman projection on quotient domains
$L^p$
-regularity of the Bergman projection on quotient domainsTo save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
 $L^p$
-regularity of the Bergman projection on quotient domains
$L^p$
-regularity of the Bergman projection on quotient domainsTo save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.
 $L^p$
-regularity of the Bergman projection on quotient domains
$L^p$
-regularity of the Bergman projection on quotient domains