Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T20:47:14.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Absolute C-Embedding of Spaces with Countable Character and Pseudocharacter Conditions

Published online by Cambridge University Press:  20 November 2018

Alan Dow
Alan Dow*
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Absolute C-embeddings have been studied extensively by C. E. Aull. We will use his notation P = C[Q] to mean that a space satisfying property Q is C-embedded in every space having property Q that it is embedded in if (and only if) it has property P. The first result of this type is due to Hewitt [5] where he proves that if Q is “Tychonoff” then P is almost compactness. Aull [2] proves that if Q is “T4 and countable pseudocharacter” or “T4 and first countable” then P is “countably compact”. In this paper we show that P is almost compactness if Q is “Tychonoff” and any of countable pseudocharacter, perfect, or first countability. Unfortunately for the last case we require the assumption that 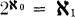. Finally we show that P is countable compactness if Q is Tychonoff and “closed sets have a countable neighborhood base”. In each of the above results C-embedding may be replaced by C*-embeddings and the results hold if restricted to closed embeddings.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 4 , April 1980 , pp. 945 - 956
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Arhangel'skiĭ, A. V., The power of bicompacta with first axiom of countability, Dokl. Akad. Nauk. SSSR 187 (1969), 967–968. (Soviet Math. Dokl. 10 (1969), 951-955).Google Scholar
2. Aull, C. E., Absolute C-embedding, Bollettino U. M. I. (5) 14-A (1977), 508–512.Google Scholar
3. Aull, C. E., Closed set axioms of countability, Akad. Van We ten 69 (1966), 311–310.Google Scholar
4. Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand, Princeton, N.J., 1960).CrossRefGoogle Scholar
5. Hewitt, E., A note on extensions of continuous functions, An. Acad. Brasil. ci. 21 (1949), 175–179.Google Scholar
6. Ostaszewski, A. J., On countably compact, perfectly normal spaces, J. London Math. Soc. (to appear).CrossRefGoogle Scholar
7. Weiss, W., Countably compact spaces and Martin's axiom, Can. J. Math. 30 (1978), 243–249.Google Scholar