Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Echterhoff, Siegfried
Lück, Wolfgang
Phillips, N. Christopher
and
Walters, Samuel
2010.
The structure of crossed products of irrational rotation algebras by finite subgroups of SL2(ℤ).
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2010,
Issue. 639,
Bönicke, Christian
Chakraborty, Sayan
He, Zhuofeng
and
Liao, Hung-Chang
2018.
Isomorphism and Morita equivalence classes for crossed products of irrational rotation algebras by cyclic subgroups of SL2(Z).
Journal of Functional Analysis,
Vol. 275,
Issue. 11,
p.
3208.

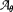 under the automorphisms
under the automorphisms 
 and
and 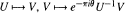 .
.