Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-01T21:44:53.403Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic Toeplitz and Composition Operators

Published online by Cambridge University Press:  20 November 2018

James A. Deddens
James A. Deddens*
Affiliation:
University of Kansas, Lawrence, Kansas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is a continuation of [1] where we began the study of intertwining analytic Toeplitz operators. Recall that X intertwines two operators A and B if XA = BX. Let H2 be the Hilbert space of analytic functions in the open unit disk D for which the functions fr(θ) = f(reiθ) are bounded in the L2 norm, and H∞ be the set of bounded functions in H2. For φ ∊ Hφ, Tφ (or Tφ(z)) is the analytic Toeplitz operator defined on H2 by the relation (Tφf)(z) = φ(z)f(z). For φ ∊ H∞, we shall denote {φ(z): |z| < 1} by Range (φ) or φ(D). Then where 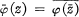and σ(Tφ) = Closure(φ(D)) [1]. If φ ∊ H∞ maps D into D, then we define the composition operator Cφ on H2 by the relation (Cφf) (z) = f(φ(z)). J. Ryff has shown [11, Theorem 1] that Cφ, is a bounded linear operator on H2.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 5 , October 1972 , pp. 859 - 865
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Deddens, J. A., Intertwining analytic Toeplitz operators, Michigan Math. J. 18 (1971), 243–246.Google Scholar
2. Douglas, R. G., On majorization, factorization and range inclusion of operators on Hilbert space, Proc. Amer. Math. Soc. 17 (1966), 413–415.Google Scholar
3. Duren, P. L., On the spectrum of a Toeplitz operator, Pacific J. Math. 14 (1964), 21–29.Google Scholar
4. Duren, P. L., Theory of Hp spaces (Academic Press, New York, 1970).Google Scholar
5. Halmos, P. R., A Hilbert space problem book (Van Nostrand, Princeton, 1967).Google Scholar
6. Hardy, G. H., Divergent series (Oxford University Press, Oxford, 1949).Google Scholar
7. Hoffman, K., Banach spaces of analytic functions (Prentice Hall, Englewood Cliffs, 1962).Google Scholar
8. Kriete, K. L. and David, Trutt, The Cesaro operator in I2 is subnormal, Amer. J. Math., 93 (1971), 215–225.Google Scholar
9. Lohwater, A. J. and Frank, Ryan, A distortion theorem for a class of conformal mappings, Mathematical essays dedicated to Maclntyre, A. J. (Ohio University Press, Athens, 1970).Google Scholar
10. Nordgren, E. A., Composition operators, Can. J. Math. 20 (1968), 442–449.Google Scholar
11. Ryff, J. V., Subordinate Hp functions, Duke Math. J., 33 (1966), 347–354.Google Scholar
12. Schwartz, H. J., Composition operators on Hp, Doctoral dissertation, University of Toledo, 1969.Google Scholar
13. Shields, A. L. and Wallen, L. J., The commutants of certain Hilbert space operators, Indiana J. Math. 20 (1971), 777–788.Google Scholar
14. Yoshino, T., Subnormal operator with a cyclic vector, Tôhoku Math. J. 21 (1969), 49–55.Google Scholar