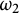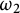1 Introduction
This work is a contribution to the study of the tension between compactness and incompactness principles in set theory. We focus on the second uncountable cardinal,
![]() $\omega _2$
, and consider the strong compactness principle of Club Stationary Reflection and the strong incompactness principle known as the Special Aronszajn Tree Property (these are defined below).
$\omega _2$
, and consider the strong compactness principle of Club Stationary Reflection and the strong incompactness principle known as the Special Aronszajn Tree Property (these are defined below).
The two properties have been shown to be consistent separately by Magidor [Reference Magidor31] and Laver and Shelah [Reference Laver and Shelah30], respectively. Since the properties represent strong forms of opposing phenomena (compactness and incompactness), it is natural to suspect that they are jointly inconsistent. The main result of this paper shows, on the contrary, that the conjunction of the two principles is consistent. More precisely, we prove the following theorem.
Theorem 1.1 It is consistent relative to the existence of an ineffable cardinal that Club Stationary Reflection and the Special Aronszajn Tree Property simultaneously hold at
![]() $\omega _2$
.
$\omega _2$
.
Our work also shows that a weaker version of stationary reflection holds in the original Laver–Shelah model (which uses a weakly compact).
Theorem 1.2 In the original Laver–Shelah model, the following stationary reflection principle holds: for every sequence
![]() $\langle S_\alpha \mid \alpha < \omega _2\rangle $
of stationary subsets of
$\langle S_\alpha \mid \alpha < \omega _2\rangle $
of stationary subsets of
![]() $\omega _2 \cap \operatorname {cof}(\omega )$
, there is
$\omega _2 \cap \operatorname {cof}(\omega )$
, there is
![]() $\beta < \omega _2$
so that
$\beta < \omega _2$
so that
![]() $S_\alpha \cap \beta $
is stationary in
$S_\alpha \cap \beta $
is stationary in
![]() $\beta $
, for every
$\beta $
, for every
![]() $\alpha < \beta $
. However, Club Stationary Reflection at
$\alpha < \beta $
. However, Club Stationary Reflection at
![]() $\omega _2$
fails.
$\omega _2$
fails.
We proceed to define the relevant terms and contextualize our result. If
![]() $\nu $
is a regular cardinal, we use
$\nu $
is a regular cardinal, we use
![]() $\operatorname {cof}(\nu )$
denote the class of ordinals with cofinality
$\operatorname {cof}(\nu )$
denote the class of ordinals with cofinality
![]() $\nu $
. We recall that if
$\nu $
. We recall that if
![]() $\operatorname {cf}(\alpha )>\omega $
, then
$\operatorname {cf}(\alpha )>\omega $
, then
![]() $S\subseteq \alpha $
is stationary if
$S\subseteq \alpha $
is stationary if
![]() $S\cap C\neq \emptyset $
for each club
$S\cap C\neq \emptyset $
for each club
![]() $C\subseteq \alpha $
. We say that S reflects if there is some
$C\subseteq \alpha $
. We say that S reflects if there is some
![]() $\beta <\alpha $
with
$\beta <\alpha $
with
![]() $\operatorname {cf}(\beta )>\omega $
so that
$\operatorname {cf}(\beta )>\omega $
so that
![]() $S\cap \beta $
is stationary in
$S\cap \beta $
is stationary in
![]() $\beta $
. If
$\beta $
. If
![]() $\kappa $
is regular, we say that stationary reflection holds at
$\kappa $
is regular, we say that stationary reflection holds at
![]() $\kappa ^{++}$
if every stationary
$\kappa ^{++}$
if every stationary
![]() $S\subseteq \kappa ^{++}\cap \operatorname {cof}(\leq \kappa )$
reflects. Baumgartner originally showed [Reference Baumgartner5] that stationary reflection at
$S\subseteq \kappa ^{++}\cap \operatorname {cof}(\leq \kappa )$
reflects. Baumgartner originally showed [Reference Baumgartner5] that stationary reflection at
![]() $\omega _2$
is consistent from a weakly compact cardinal. Harrington and Shelah [Reference Harrington and Shelah18] later improved this, showing that the optimal assumption of a Mahlo cardinal suffices. One obtains stronger principles by requiring that multiple stationary sets reflect simultaneously. Recall that a collection
$\omega _2$
is consistent from a weakly compact cardinal. Harrington and Shelah [Reference Harrington and Shelah18] later improved this, showing that the optimal assumption of a Mahlo cardinal suffices. One obtains stronger principles by requiring that multiple stationary sets reflect simultaneously. Recall that a collection
![]() $\{ S_i \mid i < \tau \}$
of
$\{ S_i \mid i < \tau \}$
of
![]() $\tau < \alpha $
stationary subsets of
$\tau < \alpha $
stationary subsets of
![]() $\alpha $
is said to reflect simultaneously if there is some
$\alpha $
is said to reflect simultaneously if there is some
![]() $\beta <\alpha $
with
$\beta <\alpha $
with
![]() $\operatorname {cf}(\beta )>\omega $
so that
$\operatorname {cf}(\beta )>\omega $
so that
![]() $S_i\cap \beta $
is stationary in
$S_i\cap \beta $
is stationary in
![]() $\beta $
for every
$\beta $
for every
![]() $i < \tau $
. Magidor [Reference Magidor31] has shown that the consistency strength of “any two stationary subsets of
$i < \tau $
. Magidor [Reference Magidor31] has shown that the consistency strength of “any two stationary subsets of
![]() $\omega _2\cap \operatorname {cof}(\omega )$
simultaneous reflect” implies the consistency of a weakly compact cardinal. One may also consider stronger diagonal versions of the above, defined in the natural way.
$\omega _2\cap \operatorname {cof}(\omega )$
simultaneous reflect” implies the consistency of a weakly compact cardinal. One may also consider stronger diagonal versions of the above, defined in the natural way.
We are interested in the following very strong form of stationary reflection which implies all of the above.
Definition 1.1 Suppose that
![]() $\kappa $
is regular. We say that Club Stationary Reflection holds at
$\kappa $
is regular. We say that Club Stationary Reflection holds at
![]() $\kappa ^{++}$
if for any stationary
$\kappa ^{++}$
if for any stationary
![]() $S\subseteq \kappa ^{++}\cap \operatorname {cof}(\leq \kappa )$
, there exists a club
$S\subseteq \kappa ^{++}\cap \operatorname {cof}(\leq \kappa )$
, there exists a club
![]() $C\subseteq \kappa ^{++}$
so that for all
$C\subseteq \kappa ^{++}$
so that for all
![]() $\beta \in C\cap \operatorname {cof}(\kappa ^+)$
, S reflects at
$\beta \in C\cap \operatorname {cof}(\kappa ^+)$
, S reflects at
![]() $\beta $
. We write
$\beta $
. We write
![]() $\mathsf {CSR}(\kappa ^{++})$
.
$\mathsf {CSR}(\kappa ^{++})$
.
We will concern ourselves with the case
![]() $\kappa =\omega $
, i.e., with stationary subsets of
$\kappa =\omega $
, i.e., with stationary subsets of
![]() $\omega _2\cap \operatorname {cof}(\omega )$
. Most relevant for us, Magidor [Reference Magidor31] showed that
$\omega _2\cap \operatorname {cof}(\omega )$
. Most relevant for us, Magidor [Reference Magidor31] showed that
![]() $\mathsf {CSR}(\omega _2)$
is consistent from a weakly compact cardinal; by the above remarks, this is the optimal hypotheses.
$\mathsf {CSR}(\omega _2)$
is consistent from a weakly compact cardinal; by the above remarks, this is the optimal hypotheses.
Extensions of
![]() $\mathsf {CSR}$
to other cardinals have been shown to have limitations. For example, Jech and Shelah [Reference Jech and Shelah22] proved that for every
$\mathsf {CSR}$
to other cardinals have been shown to have limitations. For example, Jech and Shelah [Reference Jech and Shelah22] proved that for every
![]() $n < \omega $
, if every stationary subset of
$n < \omega $
, if every stationary subset of
![]() $ \omega _{n+3} \cap \operatorname {cof}(\omega _{n+1})$
reflects, then
$ \omega _{n+3} \cap \operatorname {cof}(\omega _{n+1})$
reflects, then
![]() $\mathsf {CSR}(\omega _{n+2})$
fails. However, Jech and Shelah [Reference Jech and Shelah22], and later Cummings and Wylie [Reference Cummings and Wylie12], proved the consistency of certain best possible variations of club stationary reflection below
$\mathsf {CSR}(\omega _{n+2})$
fails. However, Jech and Shelah [Reference Jech and Shelah22], and later Cummings and Wylie [Reference Cummings and Wylie12], proved the consistency of certain best possible variations of club stationary reflection below
![]() $\aleph _\omega $
.
$\aleph _\omega $
.
Limitations on stationary reflection emerge from incompactness principles. One of the most prominent of these is Jensen’s
![]() $\square _\kappa $
. In [Reference Jensen23], Jensen showed that
$\square _\kappa $
. In [Reference Jensen23], Jensen showed that
![]() $\square _{\kappa }$
holds in L for all
$\square _{\kappa }$
holds in L for all
![]() $\kappa>\omega $
and that
$\kappa>\omega $
and that
![]() $\Box _\kappa $
implies the existence of many nonreflecting stationary subsets of
$\Box _\kappa $
implies the existence of many nonreflecting stationary subsets of
![]() $\kappa ^+$
.
$\kappa ^+$
.
Further studies showed that variations of
![]() $\square _\kappa $
place limitations on the cofinality of reflection points, as well as the amount of simultaneous reflection. For instance, in [Reference Schimmerling37], Schimmerling introduced the hierarchy of square principles,
$\square _\kappa $
place limitations on the cofinality of reflection points, as well as the amount of simultaneous reflection. For instance, in [Reference Schimmerling37], Schimmerling introduced the hierarchy of square principles,
![]() $\square _{\kappa ,\lambda }$
,
$\square _{\kappa ,\lambda }$
,
![]() $1 \leq \lambda \leq \kappa ^+$
. As
$1 \leq \lambda \leq \kappa ^+$
. As
![]() $\lambda $
increases, this hierarchy is strictly decreasing in strength; see Jensen [Reference Jensen24] for
$\lambda $
increases, this hierarchy is strictly decreasing in strength; see Jensen [Reference Jensen24] for
![]() $\kappa $
regular and [Reference Cummings, Foreman and Magidor10] for
$\kappa $
regular and [Reference Cummings, Foreman and Magidor10] for
![]() $\kappa $
singular. For a regular cardinal
$\kappa $
singular. For a regular cardinal
![]() $\kappa $
and
$\kappa $
and
![]() $\lambda \leq \kappa $
, Schimmerling and independently Foreman and Magidor have observed that if
$\lambda \leq \kappa $
, Schimmerling and independently Foreman and Magidor have observed that if
![]() $\kappa ^{<\lambda }= \kappa $
and
$\kappa ^{<\lambda }= \kappa $
and
![]() $\square _{\kappa ,<\lambda }$
hold, then every stationary subset of
$\square _{\kappa ,<\lambda }$
hold, then every stationary subset of
![]() $\kappa ^+$
has a stationary subset which does not reflect at any point of cofinality
$\kappa ^+$
has a stationary subset which does not reflect at any point of cofinality
![]() $\geq \lambda $
(see [Reference Cummings and Schimmerling11]). In particular,
$\geq \lambda $
(see [Reference Cummings and Schimmerling11]). In particular,
![]() $\kappa ^{<\kappa } =\kappa $
and
$\kappa ^{<\kappa } =\kappa $
and
![]() $\square _{\kappa ,<\kappa }$
imply that every stationary subset of
$\square _{\kappa ,<\kappa }$
imply that every stationary subset of
![]() $\kappa ^+$
has a stationary subset which does not reflect at any point in
$\kappa ^+$
has a stationary subset which does not reflect at any point in
![]() $\kappa ^+ \cap \operatorname {cof}(\kappa )$
. In [Reference Cummings, Foreman and Magidor10], Cummings, Foreman, and Magidor extended these results and developed the theory for
$\kappa ^+ \cap \operatorname {cof}(\kappa )$
. In [Reference Cummings, Foreman and Magidor10], Cummings, Foreman, and Magidor extended these results and developed the theory for
![]() $\kappa $
singular.
$\kappa $
singular.
Other notable weakenings of
![]() $\square _\kappa $
were introduced and developed by Todorčević [Reference Todorčević40]. These principles, denoted
$\square _\kappa $
were introduced and developed by Todorčević [Reference Todorčević40]. These principles, denoted
![]() $\square (\kappa ^+)$
and
$\square (\kappa ^+)$
and
![]() $ \square (\kappa ^+,\lambda )$
, place refined limitations on the extent of stationary reflection. See [Reference Fontanella and Hayut13, Reference Hayut and Lambie-Hanson20, Reference Rinot35].
$ \square (\kappa ^+,\lambda )$
, place refined limitations on the extent of stationary reflection. See [Reference Fontanella and Hayut13, Reference Hayut and Lambie-Hanson20, Reference Rinot35].
The weakest nontrivial form of square studied by Jensen is the so-called Weak Square, denoted
![]() $\square _{\kappa }^*$
, Remarkably,
$\square _{\kappa }^*$
, Remarkably,
![]() $\square _\kappa ^*$
is equivalent to a key incompactness phenomenon, the existence of a special
$\square _\kappa ^*$
is equivalent to a key incompactness phenomenon, the existence of a special
![]() $\kappa ^+$
-Aronszajn tree. Let us recall the relevant definitions. A tree is a partially ordered set
$\kappa ^+$
-Aronszajn tree. Let us recall the relevant definitions. A tree is a partially ordered set
![]() $(T,\leq _T)$
so that for each
$(T,\leq _T)$
so that for each
![]() $x\in T$
, the set of
$x\in T$
, the set of
![]() $\leq _T$
-predecessors of x is well ordered; we refer to the height of x in T as the order type of this set. If
$\leq _T$
-predecessors of x is well ordered; we refer to the height of x in T as the order type of this set. If
![]() $\alpha $
is an ordinal, we use Lev
$\alpha $
is an ordinal, we use Lev
![]() $_\alpha (T)$
to denote all
$_\alpha (T)$
to denote all
![]() $x\in T$
of height
$x\in T$
of height
![]() $\alpha $
. The height of T is the least ordinal
$\alpha $
. The height of T is the least ordinal
![]() $\alpha $
so that T has no elements of height
$\alpha $
so that T has no elements of height
![]() $\alpha $
. A branch through T is a linearly ordered subset of T, and a cofinal branch is a branch which intersects every level below the height of T.
$\alpha $
. A branch through T is a linearly ordered subset of T, and a cofinal branch is a branch which intersects every level below the height of T.
Let
![]() $\kappa $
be regular. A
$\kappa $
be regular. A
![]() $\kappa $
-tree is a tree T of height
$\kappa $
-tree is a tree T of height
![]() $\kappa $
so that each level has size
$\kappa $
so that each level has size
![]() $<\kappa $
; we will always assume that for each such tree, each node in the tree has incompatible extensions to all higher levels.
$<\kappa $
; we will always assume that for each such tree, each node in the tree has incompatible extensions to all higher levels.
![]() $\kappa $
is said to have the tree property if every
$\kappa $
is said to have the tree property if every
![]() $\kappa $
-tree has a cofinal branch. K
$\kappa $
-tree has a cofinal branch. K
![]() $\ddot {\text {o}}$
nig showed [Reference König25] that
$\ddot {\text {o}}$
nig showed [Reference König25] that
![]() $\omega $
has the tree property, whereas Aronszajn has shown that the tree property fails at
$\omega $
has the tree property, whereas Aronszajn has shown that the tree property fails at
![]() $\omega _1$
(the result was communicated in [Reference Kurepa29]). The extent of the tree property on cardinals greater than
$\omega _1$
(the result was communicated in [Reference Kurepa29]). The extent of the tree property on cardinals greater than
![]() $\omega _1$
, a famous question of Magidor’s, is independent of
$\omega _1$
, a famous question of Magidor’s, is independent of
![]() $\mathsf {ZFC}$
. A watershed in our understanding is due to Mitchell and Silver [Reference Mitchell34], who showed that the tree property at
$\mathsf {ZFC}$
. A watershed in our understanding is due to Mitchell and Silver [Reference Mitchell34], who showed that the tree property at
![]() $\omega _2$
is consistent from a weakly compact cardinal.
$\omega _2$
is consistent from a weakly compact cardinal.
A tree which witnesses the failure of the tree property is said to be Aronszajn (i.e., a
![]() $\kappa $
-tree which has no cofinal branches); the existence of such a tree is an instance of incompactness. A particularly strong witness that a tree is Aronszajn is given by a specializing function: in the case that
$\kappa $
-tree which has no cofinal branches); the existence of such a tree is an instance of incompactness. A particularly strong witness that a tree is Aronszajn is given by a specializing function: in the case that
![]() $\kappa =\lambda ^+$
, a specializing function is an
$\kappa =\lambda ^+$
, a specializing function is an
![]() $f:T\longrightarrow \lambda $
so that if
$f:T\longrightarrow \lambda $
so that if
![]() $x<_Ty$
, then
$x<_Ty$
, then
![]() $f(x)\neq f(y)$
. (For an exploration of these concepts at an arbitrarily regular cardinal, see [Reference Krueger27].) Having a specializing function is a particularly strong witness to being Aronszajn since the function witnesses that T remains Aronszajn in any extension of that model in which
$f(x)\neq f(y)$
. (For an exploration of these concepts at an arbitrarily regular cardinal, see [Reference Krueger27].) Having a specializing function is a particularly strong witness to being Aronszajn since the function witnesses that T remains Aronszajn in any extension of that model in which
![]() $\kappa $
is still a cardinal. T is said to be a special Aronszajn tree if there is a specializing function for T. The property of interest to us is the following.
$\kappa $
is still a cardinal. T is said to be a special Aronszajn tree if there is a specializing function for T. The property of interest to us is the following.
Definition 1.2 Let
![]() $\kappa $
be regular. We say that
$\kappa $
be regular. We say that
![]() $\kappa ^+$
has the Special Aronszajn Tree Property if there are Aronszajn trees on
$\kappa ^+$
has the Special Aronszajn Tree Property if there are Aronszajn trees on
![]() $\kappa ^+$
, and if every Aronszajn tree on
$\kappa ^+$
, and if every Aronszajn tree on
![]() $\kappa ^+$
is special. We denote this property by
$\kappa ^+$
is special. We denote this property by
![]() $\mathsf {SATP}(\kappa ^+)$
.
$\mathsf {SATP}(\kappa ^+)$
.
By a result of Specker [Reference Specker39], if
![]() $\kappa ^{<\kappa }$
holds, then there is a special Aronszajn tree on
$\kappa ^{<\kappa }$
holds, then there is a special Aronszajn tree on
![]() $\kappa ^+$
; in particular, if the
$\kappa ^+$
; in particular, if the
![]() $\mathsf {CH}$
holds, then there is a special Aronszajn tree on
$\mathsf {CH}$
holds, then there is a special Aronszajn tree on
![]() $\omega _2$
. Jensen [Reference Jensen23] later showed that the principle
$\omega _2$
. Jensen [Reference Jensen23] later showed that the principle
![]() $\Box ^*_\kappa $
holds if and only if there is a special Aronszajn tree on
$\Box ^*_\kappa $
holds if and only if there is a special Aronszajn tree on
![]() $\kappa ^+$
; since
$\kappa ^+$
; since
![]() $\kappa ^{<\kappa }$
implies
$\kappa ^{<\kappa }$
implies
![]() $\Box ^*_\kappa $
, this strengthens Specker’s result.
$\Box ^*_\kappa $
, this strengthens Specker’s result.
With regard to constructing specializing functions by forcing, Baumgartner, Malitz, and Reinhardt showed [Reference Baumgartner, Malitz and Reinhard7] that
![]() $\mathsf {MA}+\neg \mathsf {CH}$
implies
$\mathsf {MA}+\neg \mathsf {CH}$
implies
![]() $\mathsf {SATP}(\omega _1)$
. Later, Laver and Shelah showed [Reference Laver and Shelah30] that
$\mathsf {SATP}(\omega _1)$
. Later, Laver and Shelah showed [Reference Laver and Shelah30] that
![]() $\mathsf {SATP}(\omega _2)$
is consistent from a weakly compact cardinal. Generalizing this further, Golshani and Hayut have recently shown [Reference Golshani and Hayut17], using posets which specialize with anticipation, that it is consistent that, simultaneously, for every regular cardinal
$\mathsf {SATP}(\omega _2)$
is consistent from a weakly compact cardinal. Generalizing this further, Golshani and Hayut have recently shown [Reference Golshani and Hayut17], using posets which specialize with anticipation, that it is consistent that, simultaneously, for every regular cardinal
![]() $\kappa $
,
$\kappa $
,
![]() $\mathsf {SATP}(\kappa ^+)$
holds. Krueger has generalized the result of Laver–Shelah (and also Abraham–Shelah [Reference Abraham and Shelah2]) in a different direction [Reference Krueger28], showing that it is consistent with the
$\mathsf {SATP}(\kappa ^+)$
holds. Krueger has generalized the result of Laver–Shelah (and also Abraham–Shelah [Reference Abraham and Shelah2]) in a different direction [Reference Krueger28], showing that it is consistent with the
![]() $\mathsf {CH}$
that any two countably closed Aronszajn trees on
$\mathsf {CH}$
that any two countably closed Aronszajn trees on
![]() $\omega _2$
are club isomorphic. And finally, Asperó and Golshani [Reference Asperó and Golshani3] have announced a positive solution to the question of whether
$\omega _2$
are club isomorphic. And finally, Asperó and Golshani [Reference Asperó and Golshani3] have announced a positive solution to the question of whether
![]() $\mathsf {SATP}(\omega _2)$
is consistent with the
$\mathsf {SATP}(\omega _2)$
is consistent with the
![]() $\mathsf {GCH}$
. This work continues the study of the tension between different manifestations of compactness and incompactness phenomena in set theory, which together with the study of tension with other fundamental principles, such as approximation principles (e.g., [Reference Ben-Neria8, Reference Goldberg16]) and cardinal arithmetic (e.g., [Reference Foreman and Todorčević14, Reference Shelah38]), is central to our understanding of their extent and limitations.
$\mathsf {GCH}$
. This work continues the study of the tension between different manifestations of compactness and incompactness phenomena in set theory, which together with the study of tension with other fundamental principles, such as approximation principles (e.g., [Reference Ben-Neria8, Reference Goldberg16]) and cardinal arithmetic (e.g., [Reference Foreman and Todorčević14, Reference Shelah38]), is central to our understanding of their extent and limitations.
We proceed to describe our result in general terms and highlight the challenges that appear in the process. Let
![]() $\kappa $
be a cardinal which is either ineffable or weakly compact in a ground model V of
$\kappa $
be a cardinal which is either ineffable or weakly compact in a ground model V of
![]() $\mathsf {GCH}$
; we will specify later (Definition 2.8
) exactly when
$\mathsf {GCH}$
; we will specify later (Definition 2.8
) exactly when
![]() $\kappa $
is ineffable or weakly compact. We obtain the model which witnesses Theorem 1.1 by first defining, in the extension by
$\kappa $
is ineffable or weakly compact. We obtain the model which witnesses Theorem 1.1 by first defining, in the extension by
![]() $\mathbb {P} = \operatorname {Col}(\omega _1,<\kappa )$
, a
$\mathbb {P} = \operatorname {Col}(\omega _1,<\kappa )$
, a
![]() $\kappa ^+$
-length iteration
$\kappa ^+$
-length iteration
![]() $\mathbb {C}_{\kappa ^+} = \langle \mathbb {C}_\tau , \mathbb {C}(\tau ) \mid \tau < \kappa ^+\rangle $
of adding clubs which will eventually witnesses
$\mathbb {C}_{\kappa ^+} = \langle \mathbb {C}_\tau , \mathbb {C}(\tau ) \mid \tau < \kappa ^+\rangle $
of adding clubs which will eventually witnesses
![]() $\mathsf {CSR}(\omega _2)$
.
$\mathsf {CSR}(\omega _2)$
.
After forcing with
![]() $\mathbb {C}_{\kappa ^+}$
, we then force with a
$\mathbb {C}_{\kappa ^+}$
, we then force with a
![]() $\kappa ^+$
-iteration
$\kappa ^+$
-iteration
![]() $\mathbb {S}_{\kappa ^+} = \langle \mathbb {S}_\tau ,\mathbb {S}(\tau ) \mid \tau < \kappa ^+\rangle $
specializing the desired Aronszajn trees
$\mathbb {S}_{\kappa ^+} = \langle \mathbb {S}_\tau ,\mathbb {S}(\tau ) \mid \tau < \kappa ^+\rangle $
specializing the desired Aronszajn trees
![]() $\dot {T}_\tau $
, i.e.,
$\dot {T}_\tau $
, i.e.,
![]() $\mathbb {S}(\tau ) = \mathbb {S}(\dot {T_\tau })$
(see Section 1.2 for precise definitions of the posets).
$\mathbb {S}(\tau ) = \mathbb {S}(\dot {T_\tau })$
(see Section 1.2 for precise definitions of the posets).
To make this strategy work, we need, among other things, that all stationary subsets of
![]() $\omega _2\cap \operatorname {cof}(\omega )$
which appear in the final generic extension by
$\omega _2\cap \operatorname {cof}(\omega )$
which appear in the final generic extension by
![]() $\mathbb {P} * \dot {\mathbb {C}}_{\kappa ^+} *\dot {\mathbb {S}}_{\kappa ^+}$
reflect as in the definition of
$\mathbb {P} * \dot {\mathbb {C}}_{\kappa ^+} *\dot {\mathbb {S}}_{\kappa ^+}$
reflect as in the definition of
![]() $\mathsf {CSR}(\omega _2)$
. Consequently, the club-adding posets must anticipate names for stationary sets added by the later specializing iteration. In order to carry this through, we define the names
$\mathsf {CSR}(\omega _2)$
. Consequently, the club-adding posets must anticipate names for stationary sets added by the later specializing iteration. In order to carry this through, we define the names
![]() $\dot {\mathbb {C}}_\tau $
and
$\dot {\mathbb {C}}_\tau $
and
![]() $\dot {\mathbb {S}}_\tau $
, for
$\dot {\mathbb {S}}_\tau $
, for
![]() $\tau < \kappa ^+$
, simultaneously. More precisely, for each
$\tau < \kappa ^+$
, simultaneously. More precisely, for each
![]() $\tau < \kappa ^+$
, given that the
$\tau < \kappa ^+$
, given that the
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {\mathbb {C}}_\tau $
and the
$\dot {\mathbb {C}}_\tau $
and the
![]() $(\mathbb {P}\ast \dot {\mathbb {C}}_\tau )$
-name
$(\mathbb {P}\ast \dot {\mathbb {C}}_\tau )$
-name
![]() $\dot {\mathbb {S}}_\tau $
have been defined, we use a bookkeeping function to pick the
$\dot {\mathbb {S}}_\tau $
have been defined, we use a bookkeeping function to pick the
![]() $(\mathbb {P}*\dot {\mathbb {C}}_{\tau }*\dot {\mathbb {S}}_{\tau })$
-name
$(\mathbb {P}*\dot {\mathbb {C}}_{\tau }*\dot {\mathbb {S}}_{\tau })$
-name
![]() $\dot {S_{\tau }}$
of a stationary subset of
$\dot {S_{\tau }}$
of a stationary subset of
![]() $\kappa \cap \operatorname {cof}(\omega )$
, and we set
$\kappa \cap \operatorname {cof}(\omega )$
, and we set
![]() $\dot {\mathbb {C}}(\tau )$
to be the
$\dot {\mathbb {C}}(\tau )$
to be the
![]() $(\mathbb {P}\ast \dot {\mathbb {C}}_\tau )$
-name for the poset to add, with
$(\mathbb {P}\ast \dot {\mathbb {C}}_\tau )$
-name for the poset to add, with
![]() $\dot {\mathbb {S}}_\tau $
-anticipation, the desired club. Then we select the
$\dot {\mathbb {S}}_\tau $
-anticipation, the desired club. Then we select the
![]() $(\mathbb {P}*\dot {\mathbb {C}}_{\tau +1}*\dot {\mathbb {S}}_\tau )$
-name
$(\mathbb {P}*\dot {\mathbb {C}}_{\tau +1}*\dot {\mathbb {S}}_\tau )$
-name
![]() $\dot {T}_{\tau }$
for an Aronszajn tree on
$\dot {T}_{\tau }$
for an Aronszajn tree on
![]() $\kappa $
.
$\kappa $
.
As expected, the tension between compactness and incompactness gives rise to tension between the different parts of the forcing construction. We list three notable manifestations:
(1) Working with intermediate generic extensions. A central property of the Laver–Shelah forcing [Reference Laver and Shelah30] is the existence of intermediate forcing extensions in which regular cardinals
![]() $\alpha < \kappa $
become
$\alpha < \kappa $
become
![]() $\omega _2$
and the relevant portion
$\omega _2$
and the relevant portion
![]() $\dot {T}_\tau \cap (\alpha \times \omega _1)$
of the trees are Aronszajn trees on
$\dot {T}_\tau \cap (\alpha \times \omega _1)$
of the trees are Aronszajn trees on
![]() $\alpha $
. Accompanying this is machinery for projecting conditions of
$\alpha $
. Accompanying this is machinery for projecting conditions of
![]() $\mathbb {P} * \dot {\mathbb {S}}_\tau $
to those intermediate extensions. In [Reference Laver and Shelah30], the existence of such intermediate extensions is secured by the weak compactness of
$\mathbb {P} * \dot {\mathbb {S}}_\tau $
to those intermediate extensions. In [Reference Laver and Shelah30], the existence of such intermediate extensions is secured by the weak compactness of
![]() $\kappa $
, and the fact that
$\kappa $
, and the fact that
![]() $\mathbb {P} * \dot {\mathbb {S}}_\tau $
is
$\mathbb {P} * \dot {\mathbb {S}}_\tau $
is
![]() $\kappa $
-c.c. However, in our case, the presence of the poset
$\kappa $
-c.c. However, in our case, the presence of the poset
![]() $\dot {\mathbb {C}}_\tau $
prevents the initial segment
$\dot {\mathbb {C}}_\tau $
prevents the initial segment
![]() $\mathbb {P} *\dot {\mathbb {C}}_\tau $
from being
$\mathbb {P} *\dot {\mathbb {C}}_\tau $
from being
![]() $\kappa $
-c.c. To overcome this difficulty, we use the fact that the full collapse poset
$\kappa $
-c.c. To overcome this difficulty, we use the fact that the full collapse poset
![]() $\mathbb {P}$
absorbs many restricted subforcings of
$\mathbb {P}$
absorbs many restricted subforcings of
![]() $\mathbb {P} * \dot {\mathbb {C}}_\tau $
, which allows us to place upper bounds on various generic filters of the restricted poset. We then couple this in Section 6 with a generalization of a result of Abraham’s [Reference Abraham1] that (stated in current language) if
$\mathbb {P} * \dot {\mathbb {C}}_\tau $
, which allows us to place upper bounds on various generic filters of the restricted poset. We then couple this in Section 6 with a generalization of a result of Abraham’s [Reference Abraham1] that (stated in current language) if
![]() $\dot {\mathbb {Q}}$
is an
$\dot {\mathbb {Q}}$
is an
![]() $\operatorname {Add}(\omega ,\omega _1)$
-name for an
$\operatorname {Add}(\omega ,\omega _1)$
-name for an
![]() $\omega _1$
-closed poset, then
$\omega _1$
-closed poset, then
![]() $\operatorname {Add}(\omega ,\omega _1)\ast \dot {\mathbb {Q}}$
is strongly proper. This secures the existence of sufficiently many strongly generic conditions (and, in turn, the existence of intermediate extensions).
$\operatorname {Add}(\omega ,\omega _1)\ast \dot {\mathbb {Q}}$
is strongly proper. This secures the existence of sufficiently many strongly generic conditions (and, in turn, the existence of intermediate extensions).
(2) Preservation of stationary sets by quotients. The ability to add a closed unbounded set through the reflection points
![]() $\alpha < \kappa $
of a stationary set
$\alpha < \kappa $
of a stationary set
![]() $\dot {S_\tau } \subseteq \kappa \cap \operatorname {cof}(\omega )$
hinges upon the fact that many such points exist. The ineffability (in fact, just weak compactness) of
$\dot {S_\tau } \subseteq \kappa \cap \operatorname {cof}(\omega )$
hinges upon the fact that many such points exist. The ineffability (in fact, just weak compactness) of
![]() $\kappa $
guarantees that for many
$\kappa $
guarantees that for many
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $\dot {S_\tau } \cap \alpha $
is a stationary subset of
$\dot {S_\tau } \cap \alpha $
is a stationary subset of
![]() $\alpha $
in the restricted generic extension where
$\alpha $
in the restricted generic extension where
![]() $\alpha = \omega _2$
. The forcing construction of [Reference Magidor31] uses the fact that the related quotient of
$\alpha = \omega _2$
. The forcing construction of [Reference Magidor31] uses the fact that the related quotient of
![]() $\mathbb {P} * \dot {\mathbb {C}}_\tau $
by its initial segment is
$\mathbb {P} * \dot {\mathbb {C}}_\tau $
by its initial segment is
![]() $\sigma $
-closed, and an argument of Baumgartner’s [Reference Baumgartner5] shows that
$\sigma $
-closed, and an argument of Baumgartner’s [Reference Baumgartner5] shows that
![]() $\sigma $
-closed posets preserve the stationarity of stationary sets of countable cofinality ordinals. By contrast, for us, the stationary sets
$\sigma $
-closed posets preserve the stationarity of stationary sets of countable cofinality ordinals. By contrast, for us, the stationary sets
![]() $\dot {S}_\tau $
further rely on the specializing poset
$\dot {S}_\tau $
further rely on the specializing poset
![]() $\dot {\mathbb {S}}_\tau $
, and although the poset
$\dot {\mathbb {S}}_\tau $
, and although the poset
![]() $\mathbb {P} * \dot {\mathbb {C}}_\tau *\dot {\mathbb {S}}_\tau $
is
$\mathbb {P} * \dot {\mathbb {C}}_\tau *\dot {\mathbb {S}}_\tau $
is
![]() $\sigma $
-closed, it does not in general admit
$\sigma $
-closed, it does not in general admit
![]() $\sigma $
-closed quotients by its natural restrictions to heights
$\sigma $
-closed quotients by its natural restrictions to heights
![]() $\alpha < \kappa $
. Nevertheless, in Section 4, we analyze the Laver–Shelah iteration
$\alpha < \kappa $
. Nevertheless, in Section 4, we analyze the Laver–Shelah iteration
![]() $\dot {\mathbb {S}}_\tau $
to prove that the relevant quotients preserve the stationary of
$\dot {\mathbb {S}}_\tau $
to prove that the relevant quotients preserve the stationary of
![]() $\dot {S_\tau } \cap \alpha $
for many suitable
$\dot {S_\tau } \cap \alpha $
for many suitable
![]() $\alpha < \kappa $
.
$\alpha < \kappa $
.
(3) Preservation of Aronszajn trees. The organization of the posets
![]() $\dot {\mathbb {C}}_\tau $
and
$\dot {\mathbb {C}}_\tau $
and
![]() $\dot {\mathbb {S}}_{\tau }$
, described above, guarantees that for each
$\dot {\mathbb {S}}_{\tau }$
, described above, guarantees that for each
![]() $\tau < \kappa ^+$
,
$\tau < \kappa ^+$
,
![]() $\dot {T}_\tau $
is a
$\dot {T}_\tau $
is a
![]() $(\mathbb {P} * \dot {\mathbb {C}}_{\tau +1}*\dot {\mathbb {S}}_\tau )$
-name of an Aronszajn tree on
$(\mathbb {P} * \dot {\mathbb {C}}_{\tau +1}*\dot {\mathbb {S}}_\tau )$
-name of an Aronszajn tree on
![]() $\kappa $
, which is specialized by
$\kappa $
, which is specialized by
![]() $\mathbb {P} * \dot {\mathbb {C}}_{\tau +1} * \dot {\mathbb {S}}_{\tau +1}$
.
$\mathbb {P} * \dot {\mathbb {C}}_{\tau +1} * \dot {\mathbb {S}}_{\tau +1}$
.
However, in the final forcing construction,
![]() $\mathbb {S}_{\tau +1}$
follows the extended iteration
$\mathbb {S}_{\tau +1}$
follows the extended iteration
![]() $\mathbb {P} * \dot {\mathbb {C}}_{\kappa ^+}$
, and on its face,
$\mathbb {P} * \dot {\mathbb {C}}_{\kappa ^+}$
, and on its face,
![]() $\mathbb {P} * \dot {\mathbb {C}}_{\kappa ^+} * \dot {\mathbb {S}}_{\tau }$
might introduce a cofinal branch to
$\mathbb {P} * \dot {\mathbb {C}}_{\kappa ^+} * \dot {\mathbb {S}}_{\tau }$
might introduce a cofinal branch to
![]() $T_\tau $
, causing the specializing poset
$T_\tau $
, causing the specializing poset
![]() $\mathbb {S}(\tau )$
to collapse
$\mathbb {S}(\tau )$
to collapse
![]() $\kappa $
. To guarantee that this cannot occur, an Aronszajn preservation theorem is required for the quotient of
$\kappa $
. To guarantee that this cannot occur, an Aronszajn preservation theorem is required for the quotient of
![]() $\mathbb {P} * \dot {\mathbb {C}}_{\kappa ^+} * \dot {\mathbb {S}}_\tau $
by
$\mathbb {P} * \dot {\mathbb {C}}_{\kappa ^+} * \dot {\mathbb {S}}_\tau $
by
![]() $\mathbb {P} * \dot {\mathbb {C}}_{\tau +1} * \dot {\mathbb {S}}_\tau $
. The fact that no new reals are added during the iteration, and that
$\mathbb {P} * \dot {\mathbb {C}}_{\tau +1} * \dot {\mathbb {S}}_\tau $
. The fact that no new reals are added during the iteration, and that
![]() $\dot {\mathbb {C}}_{\kappa ^+}$
is not
$\dot {\mathbb {C}}_{\kappa ^+}$
is not
![]() $\kappa $
-closed, prevents us from using known preservation arguments (for instance, those of [Reference Unger41]). Therefore, in Section 6, we develop an alternative preservation argument which fits the properties of the poset
$\kappa $
-closed, prevents us from using known preservation arguments (for instance, those of [Reference Unger41]). Therefore, in Section 6, we develop an alternative preservation argument which fits the properties of the poset
![]() $\mathbb {P} * \dot {\mathbb {C}}_{\kappa ^+}$
, and we apply them in Section 7 to show that the tree
$\mathbb {P} * \dot {\mathbb {C}}_{\kappa ^+}$
, and we apply them in Section 7 to show that the tree
![]() $T_\tau $
remains Aronszajn.
$T_\tau $
remains Aronszajn.
1.1 Structure of this work
In the rest of this section, we review relevant preliminaries regarding forcing as well as ineffable and weakly compact cardinals. The first part of the work consists of Sections 2–4. In Section 2, we develop the notion and fundamental properties of posets which are strongly proper with respect to the filter
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\kappa $
, which is either the weakly compact filter on
$\kappa $
, which is either the weakly compact filter on
![]() $\kappa $
or the filter dual to the ineffability ideal on
$\kappa $
or the filter dual to the ineffability ideal on
![]() $\kappa $
(depending on whether
$\kappa $
(depending on whether
![]() $\kappa $
is weakly compact or ineffable, respectively). We will later verify that initial segments of the form
$\kappa $
is weakly compact or ineffable, respectively). We will later verify that initial segments of the form
![]() $\mathbb {P} * \dot {\mathbb {C}}_\tau $
, for
$\mathbb {P} * \dot {\mathbb {C}}_\tau $
, for
![]() $\tau < \kappa ^+$
, are members this class. Section 3 studies an iteration of specializing posets
$\tau < \kappa ^+$
, are members this class. Section 3 studies an iteration of specializing posets
![]() $\mathbb {S}_\tau $
, following an
$\mathbb {S}_\tau $
, following an
![]() $\mathcal {F}$
-strongly proper poset
$\mathcal {F}$
-strongly proper poset
![]() $\mathbb {P}^*$
. We prove that the main results of the Laver–Shelah analysis apply in this context as well. In the case when
$\mathbb {P}^*$
. We prove that the main results of the Laver–Shelah analysis apply in this context as well. In the case when
![]() $\mathbb {P}^*$
is just the Levy collapse to make
$\mathbb {P}^*$
is just the Levy collapse to make
![]() $\kappa $
become
$\kappa $
become
![]() $\omega _2$
, we only need a weakly compact (and
$\omega _2$
, we only need a weakly compact (and
![]() $\mathcal {F}$
is the weakly compact filter). This is just the Laver–Shelah argument. However, when
$\mathcal {F}$
is the weakly compact filter). This is just the Laver–Shelah argument. However, when
![]() $\mathbb {P}^*$
becomes a more complicated poset, we needed to use the stronger assumption that
$\mathbb {P}^*$
becomes a more complicated poset, we needed to use the stronger assumption that
![]() $\kappa $
is ineffable (and
$\kappa $
is ineffable (and
![]() $\mathcal {F}$
is the filter dual to the ineffability ideal). Nevertheless, we only need the ineffability for the case when
$\mathcal {F}$
is the filter dual to the ineffability ideal). Nevertheless, we only need the ineffability for the case when
![]() $\mathbb {P}^*$
is not just the collapse, and in this case, only for the proof of Proposition 3.12 and the corollaries of that proposition. Section 4 is devoted to showing that suitable quotients of specializing iterations of the form
$\mathbb {P}^*$
is not just the collapse, and in this case, only for the proof of Proposition 3.12 and the corollaries of that proposition. Section 4 is devoted to showing that suitable quotients of specializing iterations of the form
![]() $\mathbb {P}^* * \dot {\mathbb {S}}_\tau $
, where
$\mathbb {P}^* * \dot {\mathbb {S}}_\tau $
, where
![]() $\mathbb {P}^*$
is
$\mathbb {P}^*$
is
![]() $\mathcal {F}$
-strongly proper (and in either case for
$\mathcal {F}$
-strongly proper (and in either case for
![]() $\mathcal {F}$
) preserve stationary subsets of countable cofinality ordinals.
$\mathcal {F}$
) preserve stationary subsets of countable cofinality ordinals.
In Part 2 of the paper, we construct specific posets playing the role of
![]() $\mathbb {P}^*$
above, and we prove our theorem. In Section 5, we introduce the complementary notion of posets which are completely proper with respect to
$\mathbb {P}^*$
above, and we prove our theorem. In Section 5, we introduce the complementary notion of posets which are completely proper with respect to
![]() $\mathcal {F}$
, and later we apply this analysis to
$\mathcal {F}$
, and later we apply this analysis to
![]() $\dot {\mathbb {C}}_\tau $
,
$\dot {\mathbb {C}}_\tau $
,
![]() $\tau < \kappa ^+$
. We show that the composition of the Levy collapse and a poset which is completely proper with respect to
$\tau < \kappa ^+$
. We show that the composition of the Levy collapse and a poset which is completely proper with respect to
![]() $\mathcal {F}$
is strongly proper with respect to
$\mathcal {F}$
is strongly proper with respect to
![]() $\mathcal {F}$
. Section 6 develops the main properties of the club-adding iteration
$\mathcal {F}$
. Section 6 develops the main properties of the club-adding iteration
![]() $\mathbb {C}_\tau $
. And finally, we combine the results of the previous sections in Section 7 to prove Theorem 1.1.
$\mathbb {C}_\tau $
. And finally, we combine the results of the previous sections in Section 7 to prove Theorem 1.1.
1.2 Forcing
In this subsection, we review our conventions about forcing and provide explicit definitions of posets which we will use throughout the paper.
To begin, in order to anticipate working with iterations later, we will work with preorderings (i.e., relations which are transitive and reflexive) rather than partial orders. Moreover, we will use the Jerusalem convention for forcing. Thus, we view a forcing poset as a triple
![]() $(\mathbb {Q},\leq _{\mathbb {Q}},0_{\mathbb {Q}})$
, where
$(\mathbb {Q},\leq _{\mathbb {Q}},0_{\mathbb {Q}})$
, where
![]() $\leq _{\mathbb {Q}}$
is a preordering and where
$\leq _{\mathbb {Q}}$
is a preordering and where
![]() $0_{\mathbb {Q}}$
is a smallest element; for conditions
$0_{\mathbb {Q}}$
is a smallest element; for conditions
![]() $p,q\in \mathbb {Q}$
, we will write
$p,q\in \mathbb {Q}$
, we will write
![]() $p\geq _{\mathbb {Q}} q$
to indicate that p is an extension of q. When context is clear, we will drop explicit mention of
$p\geq _{\mathbb {Q}} q$
to indicate that p is an extension of q. When context is clear, we will drop explicit mention of
![]() $\mathbb {Q}$
in
$\mathbb {Q}$
in
![]() $0_{\mathbb {Q}}$
and
$0_{\mathbb {Q}}$
and
![]() $\leq _{\mathbb {Q}}$
. Given that we are only working with preorderings rather than partial orders, we will often have conditions
$\leq _{\mathbb {Q}}$
. Given that we are only working with preorderings rather than partial orders, we will often have conditions
![]() $p,q\in \mathbb {Q}$
so that
$p,q\in \mathbb {Q}$
so that
![]() $p\leq _{\mathbb {Q}} q$
and
$p\leq _{\mathbb {Q}} q$
and
![]() $q\leq _{\mathbb {Q}} p$
, but q and p are not literally equal as sets. In this case, we will write
$q\leq _{\mathbb {Q}} p$
, but q and p are not literally equal as sets. In this case, we will write
![]() $p=^*_{\mathbb {Q}} q$
, or simply
$p=^*_{\mathbb {Q}} q$
, or simply
![]() $p=^*q$
if
$p=^*q$
if
![]() $\mathbb {Q}$
is clear from context.
$\mathbb {Q}$
is clear from context.
If
![]() $\mathbb {Q}$
is a poset, we say that
$\mathbb {Q}$
is a poset, we say that
![]() $\mathbb {Q}$
is
$\mathbb {Q}$
is
![]() $\omega _1$
-closed with sups if for any increasing sequence
$\omega _1$
-closed with sups if for any increasing sequence
![]() $\langle q_n:n\in \omega \rangle $
of conditions in
$\langle q_n:n\in \omega \rangle $
of conditions in
![]() $\mathbb {Q}$
, there exists a
$\mathbb {Q}$
, there exists a
![]() $\leq _{\mathbb {Q}}$
-least upper bound q of the sequence. Any such q is referred to as a sup of the sequence. Note that this does not say that any two compatible conditions in
$\leq _{\mathbb {Q}}$
-least upper bound q of the sequence. Any such q is referred to as a sup of the sequence. Note that this does not say that any two compatible conditions in
![]() $\mathbb {Q}$
have a sup. Moreover, it also does not require that a sup of an increasing
$\mathbb {Q}$
have a sup. Moreover, it also does not require that a sup of an increasing
![]() $\omega $
-sequence is unique. However, if
$\omega $
-sequence is unique. However, if
![]() $q_1$
and
$q_1$
and
![]() $q_2$
are two sups of such a sequence, then
$q_2$
are two sups of such a sequence, then
![]() $q_1=^*_{\mathbb {Q}} q_2$
. These observations will be important later when we deal with iterations of posets with this property.
$q_1=^*_{\mathbb {Q}} q_2$
. These observations will be important later when we deal with iterations of posets with this property.
If
![]() $\mathbb {Q}$
is a poset and
$\mathbb {Q}$
is a poset and
![]() $q\in \mathbb {Q}$
, then we use
$q\in \mathbb {Q}$
, then we use
![]() $\mathbb {Q}/q$
to denote all conditions in
$\mathbb {Q}/q$
to denote all conditions in
![]() $\mathbb {Q}$
which extend q.
$\mathbb {Q}$
which extend q.
Let
![]() $M \prec H(\theta )$
be an elementary substructure, and let
$M \prec H(\theta )$
be an elementary substructure, and let
![]() $\mathbb {U} \in M$
be a poset. A condition u in
$\mathbb {U} \in M$
be a poset. A condition u in
![]() $\mathbb {U}$
is
$\mathbb {U}$
is
![]() $(M,\mathbb {U})$
-completely generic, if the set
$(M,\mathbb {U})$
-completely generic, if the set
![]() $\left \{ \bar {u}\in \mathbb {U}\cap M:u\geq \bar {u}\right \}$
of weaker conditions in M meets all dense subsets
$\left \{ \bar {u}\in \mathbb {U}\cap M:u\geq \bar {u}\right \}$
of weaker conditions in M meets all dense subsets
![]() $D \subseteq \mathbb {U}$
which belong to M, and thus forms an
$D \subseteq \mathbb {U}$
which belong to M, and thus forms an
![]() $(M,\mathbb {U})$
-generic filter.
$(M,\mathbb {U})$
-generic filter.
For the remainder of the paper, we fix a cardinal
![]() $\kappa $
which will be either weakly compact or ineffable (we specify in Definition 2.8 exactly when
$\kappa $
which will be either weakly compact or ineffable (we specify in Definition 2.8 exactly when
![]() $\kappa $
is ineffable or weakly compact). In the next subsection, we will review facts about ineffability and weak compactness.
$\kappa $
is ineffable or weakly compact). In the next subsection, we will review facts about ineffability and weak compactness.
Throughout the paper, we will use
![]() $\mathbb {P}$
to denote the Levy collapse
$\mathbb {P}$
to denote the Levy collapse
![]() $\operatorname {Col}(\omega _1,<\kappa )$
. If
$\operatorname {Col}(\omega _1,<\kappa )$
. If
![]() $\alpha <\kappa $
is inaccessible, we use
$\alpha <\kappa $
is inaccessible, we use
![]() $\mathbb {P}\upharpoonright \alpha $
to denote the collapse
$\mathbb {P}\upharpoonright \alpha $
to denote the collapse
![]() $\operatorname {Col}(\omega _1,<\alpha )$
. We view conditions in
$\operatorname {Col}(\omega _1,<\alpha )$
. We view conditions in
![]() $\operatorname {Col}(\omega _1,<\kappa )$
as countable functions p so that
$\operatorname {Col}(\omega _1,<\kappa )$
as countable functions p so that
![]() $\operatorname {dom}(p)\subseteq \kappa $
and so that for each
$\operatorname {dom}(p)\subseteq \kappa $
and so that for each
![]() $\nu \in \operatorname {dom}(p)$
,
$\nu \in \operatorname {dom}(p)$
,
![]() $p(\nu )$
is a countable, partial function from
$p(\nu )$
is a countable, partial function from
![]() $\omega _1$
to
$\omega _1$
to
![]() $\nu $
. If G is a V-generic filter over
$\nu $
. If G is a V-generic filter over
![]() $\mathbb {P}$
, then we use
$\mathbb {P}$
, then we use
![]() $G\upharpoonright \alpha $
to denote the V-generic filter
$G\upharpoonright \alpha $
to denote the V-generic filter
![]() $\left \{ p\upharpoonright \alpha :p\in G\right \}$
over
$\left \{ p\upharpoonright \alpha :p\in G\right \}$
over
![]() $\mathbb {P}\upharpoonright \alpha $
.
$\mathbb {P}\upharpoonright \alpha $
.
For adding clubs, we generalize the club-adding poset of Magidor [Reference Magidor31] by incorporating anticipation; we only state the definition in the generality needed for our paper. Recall that if S is stationary in
![]() $\alpha $
, then the trace of S, denoted
$\alpha $
, then the trace of S, denoted
![]() $\operatorname {tr}(S)$
, consists of all
$\operatorname {tr}(S)$
, consists of all
![]() $\beta <\alpha $
so that S reflects at
$\beta <\alpha $
so that S reflects at
![]() $\beta $
.
$\beta $
.
Definition 1.3 Let
![]() $\mathbb {S}$
be a cardinal-preserving poset in some model W, and let
$\mathbb {S}$
be a cardinal-preserving poset in some model W, and let
![]() $\dot {S}$
be an
$\dot {S}$
be an
![]() $\mathbb {S}$
-name for a stationary subset of
$\mathbb {S}$
-name for a stationary subset of
![]() $\omega _2\cap \operatorname {cof}(\omega )$
. We let
$\omega _2\cap \operatorname {cof}(\omega )$
. We let
![]() $\mathsf {CU}(\dot {S},\mathbb {S})$
denote the poset, defined in W, where conditions are closed, bounded subsets c of
$\mathsf {CU}(\dot {S},\mathbb {S})$
denote the poset, defined in W, where conditions are closed, bounded subsets c of
![]() $\omega _2$
so that
$\omega _2$
so that
The ordering is end-extension.
We emphasize that in order to be a condition in
![]() $\mathsf {CU}(\dot {S},\mathbb {S})$
, a given closed, bounded subset of
$\mathsf {CU}(\dot {S},\mathbb {S})$
, a given closed, bounded subset of
![]() $\omega _2$
must be outright forced by
$\omega _2$
must be outright forced by
![]() $\mathbb {S}$
to be contained, mod cofinality
$\mathbb {S}$
to be contained, mod cofinality
![]() $\omega $
points, in
$\omega $
points, in
![]() $\operatorname {tr}(\dot {S})$
. Since any condition c in
$\operatorname {tr}(\dot {S})$
. Since any condition c in
![]() $\mathsf {CU}(\dot {S},\mathbb {S})$
can be extended by placing an ordinal of cofinality
$\mathsf {CU}(\dot {S},\mathbb {S})$
can be extended by placing an ordinal of cofinality
![]() $\omega $
above
$\omega $
above
![]() $\max (c)$
, we see that
$\max (c)$
, we see that
![]() $\mathsf {CU}(\dot {S},\mathbb {S})$
does add a club subset of
$\mathsf {CU}(\dot {S},\mathbb {S})$
does add a club subset of
![]() $\omega _2$
of the model. Moreover, the poset is trivially
$\omega _2$
of the model. Moreover, the poset is trivially
![]() $\omega _1$
-closed, so preserves
$\omega _1$
-closed, so preserves
![]() $\omega _1$
. However, preservation of
$\omega _1$
. However, preservation of
![]() $\omega _2$
is a nontrivial matter.
$\omega _2$
is a nontrivial matter.
We now review the definition of the poset which we will use to specialize Aronszajn trees on
![]() $\omega _2$
. The poset itself will decompose such a tree into a union of
$\omega _2$
. The poset itself will decompose such a tree into a union of
![]() $\omega _1$
-many antichains, which in this case is equivalent to having a specializing function.
$\omega _1$
-many antichains, which in this case is equivalent to having a specializing function.
Definition 1.4 Suppose that T is an Aronszajn tree on
![]() $\omega _2$
. Let
$\omega _2$
. Let
![]() $\mathbb {S}(T)$
denote the poset where conditions are functions f with countable domain
$\mathbb {S}(T)$
denote the poset where conditions are functions f with countable domain
![]() $\operatorname {dom}(f)\subseteq \omega _1$
, and where for each
$\operatorname {dom}(f)\subseteq \omega _1$
, and where for each
![]() $\alpha \in \operatorname {dom}(f)$
,
$\alpha \in \operatorname {dom}(f)$
,
![]() $f(\alpha )\subseteq T$
is a countable antichain in
$f(\alpha )\subseteq T$
is a countable antichain in
![]() $<_T$
. Recalling that we are using the Jerusalem convention for forcing, we say that g extends f, written
$<_T$
. Recalling that we are using the Jerusalem convention for forcing, we say that g extends f, written
![]() $f\leq g$
, if
$f\leq g$
, if
![]() $\operatorname {dom}(f)\subseteq \operatorname {dom}(g)$
and if for all
$\operatorname {dom}(f)\subseteq \operatorname {dom}(g)$
and if for all
![]() $\alpha \in \operatorname {dom}(f)$
,
$\alpha \in \operatorname {dom}(f)$
,
![]() $f(\alpha )\subseteq g(\alpha )$
.
$f(\alpha )\subseteq g(\alpha )$
.
It is clear that
![]() $\mathbb {S}(T)$
is
$\mathbb {S}(T)$
is
![]() $\omega _1$
-closed. Moreover, if a tree
$\omega _1$
-closed. Moreover, if a tree
![]() $T'$
is not Aronszajn, then the analogously defined poset
$T'$
is not Aronszajn, then the analogously defined poset
![]() $\mathbb {S}(T')$
will collapse
$\mathbb {S}(T')$
will collapse
![]() $\omega _2$
.
$\omega _2$
.
1.3 Weak compactness
In this final subsection, we review facts about the ineffability of
![]() $\kappa $
. However, we will also need various facts about the weak compactness of
$\kappa $
. However, we will also need various facts about the weak compactness of
![]() $\kappa $
, and so we begin with these.
$\kappa $
, and so we begin with these.
Definition 1.5
![]() $\mathcal {F}_{\operatorname {WC}}$
is the filter generated by subsets A of
$\mathcal {F}_{\operatorname {WC}}$
is the filter generated by subsets A of
![]() $\kappa $
for which there is some
$\kappa $
for which there is some
![]() $U \subseteq V_\kappa $
and a
$U \subseteq V_\kappa $
and a
![]() $\Pi ^1_1$
-statement
$\Pi ^1_1$
-statement
![]() $\Phi $
, satisfied by
$\Phi $
, satisfied by
![]() $(V_\kappa ,\in ,U)$
, so that
$(V_\kappa ,\in ,U)$
, so that
The filter
![]() $\mathcal {F}_{\operatorname {WC}}$
is
$\mathcal {F}_{\operatorname {WC}}$
is
![]() $\kappa $
-closed as well as normal. It will be helpful at later parts in our argument to phrase membership in the weakly compact filter in terms of embeddings. The idea will be that for a subset B of
$\kappa $
-closed as well as normal. It will be helpful at later parts in our argument to phrase membership in the weakly compact filter in terms of embeddings. The idea will be that for a subset B of
![]() $\kappa $
, where B is a member of a
$\kappa $
, where B is a member of a
![]() $\kappa $
-model M,
$\kappa $
-model M,
![]() $B\in \mathcal {F}_{\operatorname {WC}}$
iff for all M-normal ultrafilters U,
$B\in \mathcal {F}_{\operatorname {WC}}$
iff for all M-normal ultrafilters U,
![]() $\kappa \in j_U(B)$
, where
$\kappa \in j_U(B)$
, where
![]() $j_U$
is the ultrapower embedding. We make this precise in the following few items.
$j_U$
is the ultrapower embedding. We make this precise in the following few items.
Definition 1.6 Suppose that
![]() $\alpha $
is an inaccessible cardinal. We say that a transitive set M is an
$\alpha $
is an inaccessible cardinal. We say that a transitive set M is an
![]() $\alpha $
-model if
$\alpha $
-model if
![]() $M\models \mathsf {ZFC}^-$
,
$M\models \mathsf {ZFC}^-$
,
![]() $|M|=\alpha $
,
$|M|=\alpha $
,
![]() $\alpha \in M$
, and
$\alpha \in M$
, and
![]() $\,^{<\alpha }M\subseteq M$
.
$\,^{<\alpha }M\subseteq M$
.
Weak compactness is naturally associated with various embedding properties; here, we mention the following result from [Reference Hauser19].
Proposition 1.3 For any
![]() $\kappa $
-model M, there exist a
$\kappa $
-model M, there exist a
![]() $\kappa $
-model N and an elementary embedding
$\kappa $
-model N and an elementary embedding
![]() $j:M\longrightarrow N$
so that
$j:M\longrightarrow N$
so that
![]() $\operatorname {crit}(j)=\kappa $
and
$\operatorname {crit}(j)=\kappa $
and
![]() $j,M\in N$
.
$j,M\in N$
.
However, we are mostly interested in a different case, namely, when j is the elementary embeddings associated with an M-normal ultrafilter on
![]() $\kappa $
and where N is the ultrapower of M. A filter
$\kappa $
and where N is the ultrapower of M. A filter
![]() $U \subseteq \mathcal {P}(\kappa ) \cap M$
is an M-normal ultrafilter if U is an M-ultrafilter, and for every
$U \subseteq \mathcal {P}(\kappa ) \cap M$
is an M-normal ultrafilter if U is an M-ultrafilter, and for every
![]() $A \in U$
and regressive function
$A \in U$
and regressive function
![]() $f : A \to \kappa $
in M, there exists some
$f : A \to \kappa $
in M, there exists some
![]() $A' \subseteq A$
in U so that
$A' \subseteq A$
in U so that
![]() $f\upharpoonright A'$
is constant. We note that being M-normal implies that U is closed under intersections of
$f\upharpoonright A'$
is constant. We note that being M-normal implies that U is closed under intersections of
![]() $< \kappa $
-sequences in M consisting of sets in U.
$< \kappa $
-sequences in M consisting of sets in U.
It is routine to verify that each elementary embedding
![]() $j : M \to N$
as in the proposition above gives rise to an M-normal ultrafilter
$j : M \to N$
as in the proposition above gives rise to an M-normal ultrafilter
![]() $U_j = \{ A \in \mathcal {P}(\kappa ) \cap M \mid \kappa \in j(A)\}$
. Conversely, we can associate to each M-normal ultrafilter U its ultrapower embedding
$U_j = \{ A \in \mathcal {P}(\kappa ) \cap M \mid \kappa \in j(A)\}$
. Conversely, we can associate to each M-normal ultrafilter U its ultrapower embedding
![]() $j_U : M \to N \cong \operatorname {\mathrm {Ult}}(M,U)$
.
$j_U : M \to N \cong \operatorname {\mathrm {Ult}}(M,U)$
.
Proposition 1.4 Let M be a
![]() $\kappa $
-model, and let
$\kappa $
-model, and let
![]() $B \in M$
be a subset of
$B \in M$
be a subset of
![]() $\kappa $
. If
$\kappa $
. If
![]() $B \in U$
for every M-normal ultrafilter U on
$B \in U$
for every M-normal ultrafilter U on
![]() $\kappa $
, then
$\kappa $
, then
![]() $B\in \mathcal {F}_{\operatorname {WC}}$
.
$B\in \mathcal {F}_{\operatorname {WC}}$
.
Proof Let
![]() $M,B$
be as in the statement of the proposition, and fix a subset
$M,B$
be as in the statement of the proposition, and fix a subset
![]() $E_M \subseteq \kappa \times \kappa $
so that
$E_M \subseteq \kappa \times \kappa $
so that
![]() $(\kappa ,E_M)$
is isomorphic to M. To prove that
$(\kappa ,E_M)$
is isomorphic to M. To prove that
![]() $B \in \mathcal {F}_{\operatorname {WC}}$
, it suffices to show that there is a
$B \in \mathcal {F}_{\operatorname {WC}}$
, it suffices to show that there is a
![]() $\Pi ^1_1$
statement
$\Pi ^1_1$
statement
![]() $\Psi $
satisfied by
$\Psi $
satisfied by
![]() $(V_\kappa ,\in , E_M,B)$
so that the set
$(V_\kappa ,\in , E_M,B)$
so that the set
![]() $\{ \alpha <\kappa : \alpha \text { is regular and } (V_\alpha ,\in ,E_M \cap V_\alpha , B \cap \alpha ) \models \Psi \}$
is contained in B.
$\{ \alpha <\kappa : \alpha \text { is regular and } (V_\alpha ,\in ,E_M \cap V_\alpha , B \cap \alpha ) \models \Psi \}$
is contained in B.
To begin, we observe that the assertions that “
![]() $E_M$
is well-founded,” that “
$E_M$
is well-founded,” that “
![]() $(\kappa ,E_M)$
is isomorphic to a transitive
$(\kappa ,E_M)$
is isomorphic to a transitive
![]() $\kappa $
-model,” and that “B is represented in
$\kappa $
-model,” and that “B is represented in
![]() $(\kappa ,E_M)$
by
$(\kappa ,E_M)$
by
![]() $b \in \kappa $
” are all within the class of
$b \in \kappa $
” are all within the class of
![]() $\Pi ^1_1$
formulas over
$\Pi ^1_1$
formulas over
![]() $(V_\kappa ,\in ,E_M,B)$
(see [Reference Krueger26, Section 2] for details). Let
$(V_\kappa ,\in ,E_M,B)$
(see [Reference Krueger26, Section 2] for details). Let
![]() $\Phi _0$
denote their conjunction.
$\Phi _0$
denote their conjunction.
We also note that for a subset
![]() $U_M \subseteq \kappa $
, the assertion “
$U_M \subseteq \kappa $
, the assertion “
![]() $U_M$
codes a subset of
$U_M$
codes a subset of
![]() $M \cap \mathcal {P}(\kappa )$
which is an M-normal ultrafilter” is
$M \cap \mathcal {P}(\kappa )$
which is an M-normal ultrafilter” is
![]() $\Sigma ^0_\omega $
. Therefore, the assertion
$\Sigma ^0_\omega $
. Therefore, the assertion
![]() $\Phi _1$
stating that
$\Phi _1$
stating that
is
![]() $\Pi ^1_1$
. Let
$\Pi ^1_1$
. Let
![]() $\Phi $
be the conjunction
$\Phi $
be the conjunction
![]() $\Phi _0\wedge \Phi _1$
, a
$\Phi _0\wedge \Phi _1$
, a
![]() $\Pi ^1_1$
formula satisfied in
$\Pi ^1_1$
formula satisfied in
![]() $(V_\kappa ,\in ,E_M,B)$
.
$(V_\kappa ,\in ,E_M,B)$
.
Define
![]() $X:=\{ \alpha <\kappa : \alpha \text { is regular, and } (V_\alpha ,\in ,E_M \cap V_\alpha , B \cap \alpha ) \models \Phi \}$
, and we show that
$X:=\{ \alpha <\kappa : \alpha \text { is regular, and } (V_\alpha ,\in ,E_M \cap V_\alpha , B \cap \alpha ) \models \Phi \}$
, and we show that
![]() $X\subseteq B$
. Fix some
$X\subseteq B$
. Fix some
![]() $\alpha \in X$
. Then the relation
$\alpha \in X$
. Then the relation
![]() $E_M \upharpoonright \alpha = E_M \cap V_\alpha \subseteq \alpha \times \alpha $
is well founded, and it codes an
$E_M \upharpoonright \alpha = E_M \cap V_\alpha \subseteq \alpha \times \alpha $
is well founded, and it codes an
![]() $\alpha $
-model
$\alpha $
-model
![]() $M_\alpha $
with
$M_\alpha $
with
![]() $B \cap \alpha $
represented in
$B \cap \alpha $
represented in
![]() $(\alpha ,E_M\upharpoonright \alpha )$
by the same element
$(\alpha ,E_M\upharpoonright \alpha )$
by the same element
![]() $b \in \kappa $
which represents B in
$b \in \kappa $
which represents B in
![]() $(\kappa ,E_M)$
. Let
$(\kappa ,E_M)$
. Let
![]() $i_\alpha : M_\alpha \to M_\kappa $
be the elementary embedding resulting from the identifications
$i_\alpha : M_\alpha \to M_\kappa $
be the elementary embedding resulting from the identifications
![]() $M_\alpha \cong (\alpha ,E_M\upharpoonright \alpha ) \prec (\kappa ,E_M) \cong M$
. It is straightforward to verify that
$M_\alpha \cong (\alpha ,E_M\upharpoonright \alpha ) \prec (\kappa ,E_M) \cong M$
. It is straightforward to verify that
![]() $\operatorname {\mathrm {cp}}(i_\alpha ) = \alpha $
,
$\operatorname {\mathrm {cp}}(i_\alpha ) = \alpha $
,
![]() $i_\alpha (\alpha ) =\kappa $
, and
$i_\alpha (\alpha ) =\kappa $
, and
![]() $i_\alpha (B \cap \alpha ) = B$
.
$i_\alpha (B \cap \alpha ) = B$
.
It follows that
![]() $U_{\alpha } = \{ A \subseteq \alpha : \alpha \in i_\alpha (A)\}$
is an
$U_{\alpha } = \{ A \subseteq \alpha : \alpha \in i_\alpha (A)\}$
is an
![]() $M_\alpha $
-normal ultrafilter. Let
$M_\alpha $
-normal ultrafilter. Let
![]() $j_\alpha : M_\alpha \to N_\alpha $
be the induced ultrapower embedding, and let
$j_\alpha : M_\alpha \to N_\alpha $
be the induced ultrapower embedding, and let
![]() $k_\alpha : N_\alpha \to M$
be the factor map given by
$k_\alpha : N_\alpha \to M$
be the factor map given by
![]() $k_\alpha ([f]_{U_\alpha }) = i_\alpha (f)(\alpha )$
. We note that
$k_\alpha ([f]_{U_\alpha }) = i_\alpha (f)(\alpha )$
. We note that
![]() ${\operatorname {\mathrm {cp}}}(k_\alpha )> \alpha $
. Since
${\operatorname {\mathrm {cp}}}(k_\alpha )> \alpha $
. Since
![]() $(V_\alpha ,\in ,E_M\upharpoonright \alpha ,B \cap \alpha )$
satisfies
$(V_\alpha ,\in ,E_M\upharpoonright \alpha ,B \cap \alpha )$
satisfies
![]() $\Phi $
,
$\Phi $
,
![]() $B \cap \alpha \in U_\alpha $
. The last implies that
$B \cap \alpha \in U_\alpha $
. The last implies that
![]() $\alpha \in j_\alpha (B \cap \alpha )$
, which in turn implies that
$\alpha \in j_\alpha (B \cap \alpha )$
, which in turn implies that
![]() $\alpha = k_\alpha (\alpha ) \in k_\alpha \circ j_\alpha (B \cap \alpha ) = i_\alpha (B \cap \alpha ) = B$
.▪
$\alpha = k_\alpha (\alpha ) \in k_\alpha \circ j_\alpha (B \cap \alpha ) = i_\alpha (B \cap \alpha ) = B$
.▪
We now review the relevant facts about ineffable cardinals (see [Reference Baumgartner4] for the details). A cardinal
![]() $\lambda $
is ineffable if for any sequence
$\lambda $
is ineffable if for any sequence
![]() $\vec {A}=\langle A_\nu :\nu <\lambda \rangle $
so that
$\vec {A}=\langle A_\nu :\nu <\lambda \rangle $
so that
![]() $A_\nu \subseteq \nu $
for all
$A_\nu \subseteq \nu $
for all
![]() $\nu <\lambda $
, there is an
$\nu <\lambda $
, there is an
![]() $A\subseteq \lambda $
so that
$A\subseteq \lambda $
so that
![]() $\left \{\nu <\lambda :A_\nu =A\cap \nu \right \}$
is stationary in
$\left \{\nu <\lambda :A_\nu =A\cap \nu \right \}$
is stationary in
![]() $\lambda $
. Such a set A is said to be coherent for
$\lambda $
. Such a set A is said to be coherent for
![]() $\vec {A}$
.
$\vec {A}$
.
Notation 1.7 In the case that
![]() $\kappa $
is ineffable, we will denote the ineffability ideal on
$\kappa $
is ineffable, we will denote the ineffability ideal on
![]() $\kappa $
by
$\kappa $
by
![]() $\mathcal {I}_{in}$
throughout the paper, and we will let
$\mathcal {I}_{in}$
throughout the paper, and we will let
![]() $\mathcal {F}_{in}$
denote the filter on
$\mathcal {F}_{in}$
denote the filter on
![]() $\kappa $
which is dual to
$\kappa $
which is dual to
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
![]() $\mathcal {I}_{in}$
consists of all
$\mathcal {I}_{in}$
consists of all
![]() $S\subseteq \kappa $
so that for some sequence
$S\subseteq \kappa $
so that for some sequence
![]() $\vec {A}$
as above, no stationary subset of S is coherent for
$\vec {A}$
as above, no stationary subset of S is coherent for
![]() $\vec {A}$
. In the case that
$\vec {A}$
. In the case that
![]() $\kappa $
is ineffable,
$\kappa $
is ineffable,
![]() $\mathcal {I}_{in}$
is a proper, normal ideal on
$\mathcal {I}_{in}$
is a proper, normal ideal on
![]() $\kappa $
. Finally, we mention the following theorem of Baumgartner [Reference Baumgartner4, Theorem 7.2] (see [Reference Holy and Lücke21] for more information).
$\kappa $
. Finally, we mention the following theorem of Baumgartner [Reference Baumgartner4, Theorem 7.2] (see [Reference Holy and Lücke21] for more information).
Theorem 1.5 (Baumgartner)
![]() $F_{WC}$
is contained in
$F_{WC}$
is contained in
![]() $\mathcal {F}_{in}$
.
$\mathcal {F}_{in}$
.
In fact, Baumgartner showed that
![]() $\mathcal {F}_{WC}$
is contained in the filter dual to the weak ineffability ideal on
$\mathcal {F}_{WC}$
is contained in the filter dual to the weak ineffability ideal on
![]() $\kappa $
.
$\kappa $
.
Notation 1.8
![]() $\mathcal {F}$
will denote either
$\mathcal {F}$
will denote either
![]() $\mathcal {F}_{WC}$
or
$\mathcal {F}_{WC}$
or
![]() $\mathcal {F}_{in}$
throughout this paper depending on whether
$\mathcal {F}_{in}$
throughout this paper depending on whether
![]() $\kappa $
is weakly compact or ineffable, respectively.
$\kappa $
is weakly compact or ineffable, respectively.
![]() $\mathcal {I}$
denotes the ideal dual to
$\mathcal {I}$
denotes the ideal dual to
![]() $\mathcal {F}$
. We will specify in Definition 2.8 in the next section exactly when
$\mathcal {F}$
. We will specify in Definition 2.8 in the next section exactly when
![]() $\mathcal {F}$
is equal to
$\mathcal {F}$
is equal to
![]() $\mathcal {F}_{WC}$
or equal to
$\mathcal {F}_{WC}$
or equal to
![]() $\mathcal {F}_{in}$
.
$\mathcal {F}_{in}$
.
Remark 1.6
-
(1) In our paper, we only use the ineffability of
 $\kappa $
to prove Proposition 3.12 and in the corollaries of this proposition. All other results in our paper can be carried out assuming only that
$\kappa $
to prove Proposition 3.12 and in the corollaries of this proposition. All other results in our paper can be carried out assuming only that
 $\kappa $
is weakly compact.
$\kappa $
is weakly compact. -
(2) As is immediate from Theorem 1.5 and the fact that
 $\mathcal {F}$
is either
$\mathcal {F}$
is either
 $\mathcal {F}_{WC}$
or
$\mathcal {F}_{WC}$
or
 $\mathcal {F}_{in}$
, all
$\mathcal {F}_{in}$
, all
 $\mathcal {F}$
-positive sets are also
$\mathcal {F}$
-positive sets are also
 $F_{WC}$
-positive.
$F_{WC}$
-positive. -
(3) Thus, if
 $B\in \mathcal {F}^+$
and if M is a
$B\in \mathcal {F}^+$
and if M is a
 $\kappa $
-model with
$\kappa $
-model with
 $B\in M$
, then by Proposition 1.4, there is some M-normal ultrafilter U on
$B\in M$
, then by Proposition 1.4, there is some M-normal ultrafilter U on
 $\kappa $
so that
$\kappa $
so that
 $B\in U$
. We will use this fact throughout the paper.
$B\in U$
. We will use this fact throughout the paper.
As an illustration of the type of argument in (3) above, we prove the following fact which we will need in the proof of Proposition 4.4.
Lemma 1.7 Suppose that
![]() $B\in \mathcal {F}^+$
. Then
$B\in \mathcal {F}^+$
. Then
![]() $B\backslash \operatorname {tr}(B)\in \mathcal {I}$
.
$B\backslash \operatorname {tr}(B)\in \mathcal {I}$
.
Proof Suppose otherwise, for a contradiction. Then
![]() $B\backslash \operatorname {tr}(B)\in \mathcal {F}^+$
. Let
$B\backslash \operatorname {tr}(B)\in \mathcal {F}^+$
. Let
![]() $M^*$
be a
$M^*$
be a
![]() $\kappa $
-model containing B, and hence
$\kappa $
-model containing B, and hence
![]() $B\backslash \operatorname {tr}(B)$
. By Proposition 1.4, there is an
$B\backslash \operatorname {tr}(B)$
. By Proposition 1.4, there is an
![]() $M^*$
-normal ultrafilter U so that, letting
$M^*$
-normal ultrafilter U so that, letting
![]() $j:M^*\longrightarrow N$
be the ultrapower embedding,
$j:M^*\longrightarrow N$
be the ultrapower embedding,
![]() $\kappa \in j(B\backslash \operatorname {tr}(B))$
. However, B is a stationary subset of
$\kappa \in j(B\backslash \operatorname {tr}(B))$
. However, B is a stationary subset of
![]() $\kappa $
, since
$\kappa $
, since
![]() $B\in \mathcal {F}^+$
. Thus
$B\in \mathcal {F}^+$
. Thus
![]() $\kappa \in j(\operatorname {tr}(B))$
. Since
$\kappa \in j(\operatorname {tr}(B))$
. Since
![]() $\kappa \in j(B)$
also, we have
$\kappa \in j(B)$
also, we have
![]() $\kappa \in j(B)\cap j(\operatorname {tr}(B))=j(B\cap \operatorname {tr}(B))$
, which is a contradiction.▪
$\kappa \in j(B)\cap j(\operatorname {tr}(B))=j(B\cap \operatorname {tr}(B))$
, which is a contradiction.▪
2
 $\mathcal {F}$
-strongly proper posets
$\mathcal {F}$
-strongly proper posets
In this section, we transition into the main body of the paper. After briefly reviewing some important facts about strong genericity in Section 2.1, we then define, in Section 2.2, the class of
![]() $\mathcal {F}$
-strongly proper posets (see Notation 1.8 for some information about
$\mathcal {F}$
-strongly proper posets (see Notation 1.8 for some information about
![]() $\mathcal {F}$
and see Definition 2.8 for the exact definition). This class, which includes the collapse
$\mathcal {F}$
and see Definition 2.8 for the exact definition). This class, which includes the collapse
![]() $\mathbb {P}$
, consists of posets for which we may build various residue systems and thereby obtain strongly generic conditions for models of interest.
$\mathbb {P}$
, consists of posets for which we may build various residue systems and thereby obtain strongly generic conditions for models of interest.
2.1 Review of strongly generic conditions
Here, we review the definition and basic properties of strongly generic conditions. Much of this material was originally developed by Mitchell [Reference Mitchell34]. Parts of our exposition here summarize the exposition in [Reference Krueger28, Section 1], to which we refer the reader for proofs.
Definition 2.1 Let
![]() $N\prec H(\theta )$
, where
$N\prec H(\theta )$
, where
![]() $\theta $
is regular. Let
$\theta $
is regular. Let
![]() $\mathbb {Q}\in N$
be a poset. A condition
$\mathbb {Q}\in N$
be a poset. A condition
![]() $q\in \mathbb {Q}$
is said to be a strongly
$q\in \mathbb {Q}$
is said to be a strongly
![]() $(N,\mathbb {Q})$
-generic condition if for any set D which is dense in
$(N,\mathbb {Q})$
-generic condition if for any set D which is dense in
![]() $\mathbb {Q}\cap N$
, D is predense above q in
$\mathbb {Q}\cap N$
, D is predense above q in
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Remark 2.1 Note that if
![]() $\mathbb {Q}\in N$
, with N as above, then any strongly
$\mathbb {Q}\in N$
, with N as above, then any strongly
![]() $(N,\mathbb {Q})$
-generic condition is also an
$(N,\mathbb {Q})$
-generic condition is also an
![]() $(N,\mathbb {Q})$
-generic condition. Moreover, q is a strongly
$(N,\mathbb {Q})$
-generic condition. Moreover, q is a strongly
![]() $(N,\mathbb {Q})$
-generic condition iff
$(N,\mathbb {Q})$
-generic condition iff
![]() $q\Vdash _{\mathbb {Q}}\dot {G}_{\mathbb {Q}}\cap N$
is a V-generic filter over
$q\Vdash _{\mathbb {Q}}\dot {G}_{\mathbb {Q}}\cap N$
is a V-generic filter over
![]() $\mathbb {Q}\cap N$
.
$\mathbb {Q}\cap N$
.
We now review a combinatorial characterization of strongly generic conditions, implicit in [Reference Mitchell34, Proposition 2.15], in terms of the existence of residue functions.
Definition 2.2 Suppose that
![]() $\mathbb {Q}\in N\prec H(\theta )$
,
$\mathbb {Q}\in N\prec H(\theta )$
,
![]() $q\in \mathbb {Q}$
, and
$q\in \mathbb {Q}$
, and
![]() $s\in \mathbb {Q}\cap N$
. s is said to be a residue of q to N if for all
$s\in \mathbb {Q}\cap N$
. s is said to be a residue of q to N if for all
![]() $t\geq _{\mathbb {Q}\cap N}s$
, t and q are compatible in
$t\geq _{\mathbb {Q}\cap N}s$
, t and q are compatible in
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
A residue function for N above q is a function
![]() $f_N$
defined on
$f_N$
defined on
![]() $\mathbb {Q}/q$
so that for each
$\mathbb {Q}/q$
so that for each
![]() $r\in \mathbb {Q}/q$
,
$r\in \mathbb {Q}/q$
,
![]() $f_N(r)$
is a residue of r to N.
$f_N(r)$
is a residue of r to N.
Finally, if
![]() $q,r\in \mathbb {Q}$
and
$q,r\in \mathbb {Q}$
and
![]() $s\in \mathbb {Q}\cap N$
, we say that s is a dual residue of q and r to N if s is a residue for both q and r to N.
$s\in \mathbb {Q}\cap N$
, we say that s is a dual residue of q and r to N if s is a residue for both q and r to N.
Lemma 2.2
![]() $q\in \mathbb {Q}$
is
$q\in \mathbb {Q}$
is
![]() $(N,\mathbb {Q})$
-strongly generic iff there is a residue function for N above q.
$(N,\mathbb {Q})$
-strongly generic iff there is a residue function for N above q.
In the next subsection, we will isolate further properties of residue functions of interest. For now, we review the process by which strongly generic conditions allow us to break apart the forcing
![]() $\mathbb {Q}$
into a two-step iteration.
$\mathbb {Q}$
into a two-step iteration.
Notation 2.3 Let
![]() $\mathbb {Q}$
be a poset and
$\mathbb {Q}$
be a poset and
![]() $q\in \mathbb {Q}$
. Suppose
$q\in \mathbb {Q}$
. Suppose
![]() $\mathbb {Q}\in N\prec H(\theta )$
and q is a strongly
$\mathbb {Q}\in N\prec H(\theta )$
and q is a strongly
![]() $(N,\mathbb {Q})$
-generic condition. Fix a V-generic filter
$(N,\mathbb {Q})$
-generic condition. Fix a V-generic filter
![]() $\bar {G}$
over
$\bar {G}$
over
![]() $\mathbb {Q}\cap N$
. In
$\mathbb {Q}\cap N$
. In
![]() $V[\bar {G}]$
, let
$V[\bar {G}]$
, let
![]() $(\mathbb {Q}/q)/\bar {G}$
denote the poset where conditions are all
$(\mathbb {Q}/q)/\bar {G}$
denote the poset where conditions are all
![]() $r\in (\mathbb {Q}/q)$
which are
$r\in (\mathbb {Q}/q)$
which are
![]() $\mathbb {Q}$
-compatible with every condition in
$\mathbb {Q}$
-compatible with every condition in
![]() $\bar {G}$
. The ordering is the same as in
$\bar {G}$
. The ordering is the same as in
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
The following two results originate in [Reference Mitchell33]; our formulation of them follows [Reference Krueger28].
Lemma 2.3 Suppose
![]() $\mathbb {Q}\in N\prec H(\theta )$
and q is a strongly
$\mathbb {Q}\in N\prec H(\theta )$
and q is a strongly
![]() $(N,\mathbb {Q})$
-generic condition. Then, for all
$(N,\mathbb {Q})$
-generic condition. Then, for all
![]() $r\geq q$
and
$r\geq q$
and
![]() $s\in \mathbb {Q}\cap N$
, s is a residue of r to N iff
$s\in \mathbb {Q}\cap N$
, s is a residue of r to N iff
![]() $s\Vdash _{\mathbb {Q}\cap N} r\in (\mathbb {Q}/q)/\dot {G}_{\mathbb {Q}\cap N}$
.
$s\Vdash _{\mathbb {Q}\cap N} r\in (\mathbb {Q}/q)/\dot {G}_{\mathbb {Q}\cap N}$
.
Lemma 2.4 Suppose
![]() $\mathbb {Q}\in N\prec H(\theta )$
and q is a strongly
$\mathbb {Q}\in N\prec H(\theta )$
and q is a strongly
![]() $(N,\mathbb {Q})$
-generic condition. Then,
$(N,\mathbb {Q})$
-generic condition. Then,
-
(1) if
 $r\geq q$
,
$r\geq q$
,
 $s\in \mathbb {Q}\cap N$
, and r and s are
$s\in \mathbb {Q}\cap N$
, and r and s are
 $\mathbb {Q}$
-compatible, then there exists
$\mathbb {Q}$
-compatible, then there exists
 $t\geq _{\mathbb {Q}\cap N} s$
so that t is a residue of r to N; and
$t\geq _{\mathbb {Q}\cap N} s$
so that t is a residue of r to N; and -
(2) if
 $D\subseteq \mathbb {Q}$
is dense above q, then
$D\subseteq \mathbb {Q}$
is dense above q, then
 $\mathbb {Q}\cap N$
forces that
$\mathbb {Q}\cap N$
forces that
 $D\cap (\mathbb {Q}/q)/\dot {G}_{\mathbb {Q}\cap N}$
is dense in
$D\cap (\mathbb {Q}/q)/\dot {G}_{\mathbb {Q}\cap N}$
is dense in
 $(\mathbb {Q}/q)/\dot {G}_{\mathbb {Q}\cap N}$
.
$(\mathbb {Q}/q)/\dot {G}_{\mathbb {Q}\cap N}$
.
2.2 Exact residue functions and
 $\mathcal {F}$
-strong properness
$\mathcal {F}$
-strong properness
Following Neeman [Reference Gilton and Neeman15], we next isolate the properties of residue functions (see Definition 2.2) of interest. We will apply this in our work to the iteration
![]() $\mathbb {P} * \dot {\mathbb {C}}$
, consisting of the collapse poset
$\mathbb {P} * \dot {\mathbb {C}}$
, consisting of the collapse poset
![]() $\mathbb {P}$
followed by a Magidor style, club-adding iteration
$\mathbb {P}$
followed by a Magidor style, club-adding iteration
![]() $\dot {\mathbb {C}}$
. Neeman also connected this with countable closure of the quotient forcing [Reference Gilton and Neeman15, Section 2.2]. However, we were not able to apply this analysis to the final poset, which also includes the specializing iteration, as we do not know if the quotients involving the specializing iteration are even strategically closed. This will lead us later, in Section 4, to an ad hoc proof that the quotients of the final poset preserve stationary sets consisting of countable cofinality ordinals, without having
$\dot {\mathbb {C}}$
. Neeman also connected this with countable closure of the quotient forcing [Reference Gilton and Neeman15, Section 2.2]. However, we were not able to apply this analysis to the final poset, which also includes the specializing iteration, as we do not know if the quotients involving the specializing iteration are even strategically closed. This will lead us later, in Section 4, to an ad hoc proof that the quotients of the final poset preserve stationary sets consisting of countable cofinality ordinals, without having
![]() $\omega _1$
-closed quotients.
$\omega _1$
-closed quotients.
Recalling that we are working with preorders (in anticipation of working with iterations later), we begin our discussion with the following definition.
Definition 2.4 Let
![]() $\mathbb {Q}$
be a poset which is
$\mathbb {Q}$
be a poset which is
![]() $\omega _1$
-closed with sups.
$\omega _1$
-closed with sups.
![]() $D\subseteq \mathbb {Q}$
is said to be countably
$D\subseteq \mathbb {Q}$
is said to be countably
![]() $=^*$
-closed if:
$=^*$
-closed if:
-
(a) for each
 $q\in D$
and
$q\in D$
and
 $r\in \mathbb {Q}$
, if
$r\in \mathbb {Q}$
, if
 $r=^*q$
, then
$r=^*q$
, then
 $r\in D$
; and
$r\in D$
; and -
(b) if
 $\langle q_n:n\in \omega \rangle $
is an increasing sequence of conditions, all of which are in D, and if
$\langle q_n:n\in \omega \rangle $
is an increasing sequence of conditions, all of which are in D, and if
 $q^*$
is a sup of the sequence, then
$q^*$
is a sup of the sequence, then
 $q^*\in D$
.
$q^*\in D$
.
Such sets D will arise later as the domains of exact (see below) residue functions, whose domains need not, in general, be all of the poset under consideration, but only a dense,
![]() $=^*$
-closed subset. We will construct such functions in Proposition 5.4.
$=^*$
-closed subset. We will construct such functions in Proposition 5.4.
The following is Neeman’s notion of an exact strong residue function for N with dense domain above q [Reference Gilton and Neeman15, Definitions 1.6 and 2.10], but with the requirement of strategic continuity strengthened to continuity.
Definition 2.5 Let
![]() $\mathbb {Q}$
be a poset which is
$\mathbb {Q}$
be a poset which is
![]() $\omega _1$
-closed with sups, and fix N with
$\omega _1$
-closed with sups, and fix N with
![]() $\mathbb {Q}\in N\prec H(\theta )$
. Let
$\mathbb {Q}\in N\prec H(\theta )$
. Let
![]() $q\in \mathbb {Q}$
.
$q\in \mathbb {Q}$
.
A partial function
![]() $f:\mathbb {Q}/q\rightharpoonup \mathbb {Q}\cap N$
is said to be an exact, strong residue function for N above q if it satisfies the following properties:
$f:\mathbb {Q}/q\rightharpoonup \mathbb {Q}\cap N$
is said to be an exact, strong residue function for N above q if it satisfies the following properties:
-
(1) (dense domain) the domain of f is a dense, countably
 $=^*$
-closed subset D of
$=^*$
-closed subset D of
 $\mathbb {Q}/q$
;
$\mathbb {Q}/q$
; -
(2) (projection)
 $r\geq f(r)$
for all
$r\geq f(r)$
for all
 $r\in D$
;
$r\in D$
; -
(3) (order preservation) for all
 $r^*,r\in D$
, if
$r^*,r\in D$
, if
 $r^*\geq r$
, then
$r^*\geq r$
, then
 $f(r^*)\geq f(r)$
;
$f(r^*)\geq f(r)$
; -
(4) (strong residue) for any
 $r\in D$
and any
$r\in D$
and any
 $u\in \mathbb {Q}\cap N$
so that
$u\in \mathbb {Q}\cap N$
so that
 $u\geq f(r)$
, there exists
$u\geq f(r)$
, there exists
 $r^*\geq r$
with
$r^*\geq r$
with
 $r^*\in D$
so that
$r^*\in D$
so that
 $f(r^*)\geq u$
; and
$f(r^*)\geq u$
; and -
(5) (countable continuity) if
 $\langle r_n:n\in \omega \rangle $
is an increasing sequence of conditions in D with a sup
$\langle r_n:n\in \omega \rangle $
is an increasing sequence of conditions in D with a sup
 $r^*$
, then
$r^*$
, then
 $f(r^*)$
is a sup of
$f(r^*)$
is a sup of
 $\langle f(r_n):n\in \omega \rangle $
.Footnote
1
$\langle f(r_n):n\in \omega \rangle $
.Footnote
1
We call such a pair
![]() $\langle q,f\rangle $
a residue pair for
$\langle q,f\rangle $
a residue pair for
![]() $(N,\mathbb {Q})$
, or just a residue pair for N if
$(N,\mathbb {Q})$
, or just a residue pair for N if
![]() $\mathbb {Q}$
is clear from context.
$\mathbb {Q}$
is clear from context.
The following appears in [Reference Gilton and Neeman15] (Lemma 2.11).
Lemma 2.5 Suppose that
![]() $\mathbb {Q}$
is separative,
$\mathbb {Q}$
is separative,
![]() $q\in \mathbb {Q}$
, and that
$q\in \mathbb {Q}$
, and that
![]() $f:\mathbb {Q}/q\longrightarrow \mathbb {Q}\cap N$
is a function satisfying properties (2) and (4) of Definition 2.5. Then f is order-preserving on its domain.
$f:\mathbb {Q}/q\longrightarrow \mathbb {Q}\cap N$
is a function satisfying properties (2) and (4) of Definition 2.5. Then f is order-preserving on its domain.
Example 2.6 Let
![]() $\alpha <\kappa $
be inaccessible. Then the function
$\alpha <\kappa $
be inaccessible. Then the function
![]() $f:\mathbb {P}\longrightarrow \mathbb {P}\upharpoonright \alpha $
given by
$f:\mathbb {P}\longrightarrow \mathbb {P}\upharpoonright \alpha $
given by
![]() $f(p)=p\upharpoonright \alpha $
is an exact, strong residue function for any
$f(p)=p\upharpoonright \alpha $
is an exact, strong residue function for any
![]() $M\prec H(\theta )$
with
$M\prec H(\theta )$
with
![]() $M\cap \kappa =\alpha $
above the condition
$M\cap \kappa =\alpha $
above the condition
![]() $\emptyset $
and has all of
$\emptyset $
and has all of
![]() $\mathbb {P}$
as its domain.
$\mathbb {P}$
as its domain.
Our next task is to isolate the models which for us will play the role of “N” in Definition 2.5. First we have some notation which we will fix for the remainder of the paper.
Notation 2.6 Let
![]() $\lhd $
be a fixed well-order of
$\lhd $
be a fixed well-order of
![]() $H(\kappa ^+)$
.
$H(\kappa ^+)$
.
In the following definitions and claims, we make a standard use of continuous sequences of elementary substructures
![]() $M_\alpha $
, where
$M_\alpha $
, where
![]() $|M_\alpha | = \alpha < \kappa $
and
$|M_\alpha | = \alpha < \kappa $
and
![]() $M_\alpha \cap \kappa = \alpha $
, to form natural restrictions
$M_\alpha \cap \kappa = \alpha $
, to form natural restrictions
![]() $\mathbb {P}^* \cap M_\alpha $
of posets
$\mathbb {P}^* \cap M_\alpha $
of posets
![]() $\mathbb {P}^*$
which are members of the models on the chain. For ease of notation in describing such chains, we use terminology similar to [Reference Krueger28] and introduce the notion of a P-suitable sequence, for a parameter P.
$\mathbb {P}^*$
which are members of the models on the chain. For ease of notation in describing such chains, we use terminology similar to [Reference Krueger28] and introduce the notion of a P-suitable sequence, for a parameter P.
Definition 2.7 Let
![]() $P\in H(\kappa ^+)$
be a parameter. We say that a sequence
$P\in H(\kappa ^+)$
be a parameter. We say that a sequence
![]() $\langle M_\alpha :\alpha \in A\rangle $
is P-suitable if:
$\langle M_\alpha :\alpha \in A\rangle $
is P-suitable if:
-
(1)
 $A\in {\mathcal {F}^+}$
;
$A\in {\mathcal {F}^+}$
; -
(2) for each
 $\alpha \in A$
,
$\alpha \in A$
,
 $\alpha $
is inaccessible,
$\alpha $
is inaccessible,
 $M_\alpha \cap \kappa =\alpha $
,
$M_\alpha \cap \kappa =\alpha $
,
 $\,^{<\alpha }M_\alpha \subseteq M_\alpha $
, and
$\,^{<\alpha }M_\alpha \subseteq M_\alpha $
, and
 $|M_\alpha |=\alpha $
;
$|M_\alpha |=\alpha $
; -
(3) for each
 $\alpha \in A$
,
$\alpha \in A$
,
 $M_\alpha \prec (H(\kappa ^+),\in ,\lhd )$
and
$M_\alpha \prec (H(\kappa ^+),\in ,\lhd )$
and
 $P\in M_\alpha $
; and
$P\in M_\alpha $
; and -
(4) if
 $\alpha <\beta $
are in A, then
$\alpha <\beta $
are in A, then
 $M_\alpha \in M_\beta $
, and also if
$M_\alpha \in M_\beta $
, and also if
 $\gamma \in A\cap \lim (A)$
, then
$\gamma \in A\cap \lim (A)$
, then
 $M_\gamma =\bigcup \left \{ M_\delta :\delta \in A\cap \gamma \right \}$
.
$M_\gamma =\bigcup \left \{ M_\delta :\delta \in A\cap \gamma \right \}$
.
We refer to a single model M satisfying (2) and (3) as a P-suitable model.
It is clear from the definition that if
![]() $\vec {M}$
is P-suitable and
$\vec {M}$
is P-suitable and
![]() $B\subseteq \operatorname {dom}(\vec {M})$
is in
$B\subseteq \operatorname {dom}(\vec {M})$
is in
![]() $\mathcal {F}^+$
, then
$\mathcal {F}^+$
, then
![]() $\langle M_\alpha :\alpha \in B\rangle $
is also P-suitable. It is also clear that for any
$\langle M_\alpha :\alpha \in B\rangle $
is also P-suitable. It is also clear that for any
![]() $P\in H(\kappa ^+)$
, there exists a P-suitable sequence.
$P\in H(\kappa ^+)$
, there exists a P-suitable sequence.
The next definition is the main item of this section; it specifies a class of posets which contains the Levy collapse
![]() $\mathbb {P}$
and each of which can play the role of a preparatory forcing for a
$\mathbb {P}$
and each of which can play the role of a preparatory forcing for a
![]() $\aleph _2$
-c.c. iteration specializing Aronszajn trees. (The work in Section 3 is devoted to showing this.) It is helpful to recall Notation 1.7.
$\aleph _2$
-c.c. iteration specializing Aronszajn trees. (The work in Section 3 is devoted to showing this.) It is helpful to recall Notation 1.7.
Definition 2.8 Let
![]() $\mathbb {P}^*$
be a poset in
$\mathbb {P}^*$
be a poset in
![]() $H(\kappa ^+)$
which is
$H(\kappa ^+)$
which is
![]() $\omega _1$
-closed with sups and which collapses all cardinals in the interval
$\omega _1$
-closed with sups and which collapses all cardinals in the interval
![]() $(\omega _1,\kappa )$
. In the case that
$(\omega _1,\kappa )$
. In the case that
![]() $\mathbb {P}^*=\mathbb {P}$
(recall that
$\mathbb {P}^*=\mathbb {P}$
(recall that
![]() $\mathbb {P}=\operatorname {Col}(\omega _1,<\kappa )$
), we assume that
$\mathbb {P}=\operatorname {Col}(\omega _1,<\kappa )$
), we assume that
![]() $\kappa $
is weakly compact, and in the case that
$\kappa $
is weakly compact, and in the case that
![]() $\mathbb {P}^*$
is not
$\mathbb {P}^*$
is not
![]() $\mathbb {P}$
, we assume that
$\mathbb {P}$
, we assume that
![]() $\kappa $
is ineffable. Let
$\kappa $
is ineffable. Let
![]() $\mathcal {F}$
denote the following filter on
$\mathcal {F}$
denote the following filter on
![]() $\kappa $
:
$\kappa $
:
 $$ \begin{align*}{\mathcal{F}=}\begin{cases} {\mathcal{F}_{WC}}, & {\text{if }\mathbb{P}^*=\mathbb{P}},\\ {\mathcal{F}_{in}}, & {\text{otherwise,}} \end{cases} \end{align*} $$
$$ \begin{align*}{\mathcal{F}=}\begin{cases} {\mathcal{F}_{WC}}, & {\text{if }\mathbb{P}^*=\mathbb{P}},\\ {\mathcal{F}_{in}}, & {\text{otherwise,}} \end{cases} \end{align*} $$
and let
![]() $\mathcal {I}$
denote the ideal dual to
$\mathcal {I}$
denote the ideal dual to
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
We say that
![]() $\mathbb {P}^*$
is
$\mathbb {P}^*$
is
![]() $\mathcal {F}$
-strongly proper if for any
$\mathcal {F}$
-strongly proper if for any
![]() $\mathbb {P}^*$
-suitable sequence
$\mathbb {P}^*$
-suitable sequence
![]() $\vec {M}$
, there exist an
$\vec {M}$
, there exist an
![]() $A\subseteq \operatorname {dom}(\vec {M})$
with
$A\subseteq \operatorname {dom}(\vec {M})$
with
![]() $\operatorname {dom}(\vec {M})\backslash A\in \mathcal {I}$
, a sequence
$\operatorname {dom}(\vec {M})\backslash A\in \mathcal {I}$
, a sequence
![]() $\langle p^*(M_\alpha ):\alpha \in A\rangle $
of conditions in
$\langle p^*(M_\alpha ):\alpha \in A\rangle $
of conditions in
![]() $\mathbb {P}^*$
, and a sequence
$\mathbb {P}^*$
, and a sequence
![]() $\langle \varphi ^{M_\alpha }:\alpha \in A\rangle $
of functions satisfying the following properties, for each
$\langle \varphi ^{M_\alpha }:\alpha \in A\rangle $
of functions satisfying the following properties, for each
![]() $\alpha \in A$
:
$\alpha \in A$
:
-
(1)
 $\varphi ^{M_\alpha }$
is an exact, strong residue function for
$\varphi ^{M_\alpha }$
is an exact, strong residue function for
 $(M_\alpha ,\mathbb {P}^*)$
above
$(M_\alpha ,\mathbb {P}^*)$
above
 $p^*(M_\alpha )$
and
$p^*(M_\alpha )$
and
 $\varphi ^{M_\alpha }(p^*(M_\alpha ))=0_{\mathbb {P}^*}$
; and
$\varphi ^{M_\alpha }(p^*(M_\alpha ))=0_{\mathbb {P}^*}$
; and -
(2) if
 $\beta \in A$
is greater than
$\beta \in A$
is greater than
 $\alpha $
, then
$\alpha $
, then
 $p^*(M_\alpha )$
and
$p^*(M_\alpha )$
and
 $\varphi ^{M_\alpha }$
are members of
$\varphi ^{M_\alpha }$
are members of
 $M_\beta $
.
$M_\beta $
.
We will refer to the sequence of pairs
![]() $\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in A\rangle $
as a residue system for
$\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in A\rangle $
as a residue system for
![]() $\vec {M}\upharpoonright A$
and
$\vec {M}\upharpoonright A$
and
![]() $\mathbb {P}^*$
.
$\mathbb {P}^*$
.
Remark 2.7
-
(1) A corollary of (1) of the above definition is that
 $p^*(M_\alpha )$
is compatible with every condition in
$p^*(M_\alpha )$
is compatible with every condition in
 $\mathbb {P}^*\cap M_\alpha $
. Such conditions were called universal in [Reference Cox and Krueger9].
$\mathbb {P}^*\cap M_\alpha $
. Such conditions were called universal in [Reference Cox and Krueger9]. -
(2) Note that any
 $\mathcal {F}$
-strongly proper poset has size exactly
$\mathcal {F}$
-strongly proper poset has size exactly
 $\kappa $
. It has size at least
$\kappa $
. It has size at least
 $\kappa $
since the
$\kappa $
since the
 $\mathsf {GCH}$
holds and it collapses all cardinals in the interval
$\mathsf {GCH}$
holds and it collapses all cardinals in the interval
 $(\omega _1,\kappa )$
and has size no more than
$(\omega _1,\kappa )$
and has size no more than
 $\kappa $
since it is a member of
$\kappa $
since it is a member of
 $H(\kappa ^+)$
.
$H(\kappa ^+)$
.
Example 2.8 The Levy collapse poset
![]() $\mathbb {P}$
is an example of an
$\mathbb {P}$
is an example of an
![]() $\mathcal {F}$
-strongly proper poset (noting that
$\mathcal {F}$
-strongly proper poset (noting that
![]() $\mathcal {F}=\mathcal {F}_{WC}$
in this case). Indeed, letting
$\mathcal {F}=\mathcal {F}_{WC}$
in this case). Indeed, letting
![]() $\vec {M}$
be any suitable sequence, we may take the set A in Definition 2.8 to just be
$\vec {M}$
be any suitable sequence, we may take the set A in Definition 2.8 to just be
![]() $\operatorname {dom}(\vec {M})$
. Then we define
$\operatorname {dom}(\vec {M})$
. Then we define
![]() $p(M_\alpha ):=\emptyset $
for all
$p(M_\alpha ):=\emptyset $
for all
![]() $\alpha \in A$
and define
$\alpha \in A$
and define
![]() $\varphi ^{M_\alpha }$
on the entire poset
$\varphi ^{M_\alpha }$
on the entire poset
![]() $\mathbb {P}$
by
$\mathbb {P}$
by
![]() $\varphi ^{M_\alpha }(p)=p\upharpoonright \alpha $
. As stated in Example 2.6, each
$\varphi ^{M_\alpha }(p)=p\upharpoonright \alpha $
. As stated in Example 2.6, each
![]() $\varphi ^{M_\alpha }$
is an exact, strong residue function for
$\varphi ^{M_\alpha }$
is an exact, strong residue function for
![]() $M_\alpha $
above
$M_\alpha $
above
![]() $\emptyset $
. The remaining properties of Definition 2.8 are trivial.
$\emptyset $
. The remaining properties of Definition 2.8 are trivial.
In our intended applications, the posets playing the role of
![]() $\mathbb {P}^*$
in Definition 2.8 will be of the form
$\mathbb {P}^*$
in Definition 2.8 will be of the form
![]() $\mathbb {P}\ast \dot {\mathbb {C}}$
, where
$\mathbb {P}\ast \dot {\mathbb {C}}$
, where
![]() $\dot {\mathbb {C}}$
is a
$\dot {\mathbb {C}}$
is a
![]() $\mathbb {P}$
-name for an iteration of club adding with anticipation.
$\mathbb {P}$
-name for an iteration of club adding with anticipation.
We now check, by a standard argument, that forcing with an
![]() $\mathcal {F}$
-strongly proper poset preserves
$\mathcal {F}$
-strongly proper poset preserves
![]() $\kappa $
.
$\kappa $
.
Lemma 2.9 Suppose that
![]() $\mathbb {P}^*$
is
$\mathbb {P}^*$
is
![]() $\mathcal {F}$
-strongly proper. Then forcing with
$\mathcal {F}$
-strongly proper. Then forcing with
![]() $\mathbb {P}^*$
preserves
$\mathbb {P}^*$
preserves
![]() $\kappa $
.
$\kappa $
.
Proof By Definition 2.8, we know that
![]() $\mathbb {P}^*$
preserves
$\mathbb {P}^*$
preserves
![]() $\omega _1$
and collapses all cardinals in the interval
$\omega _1$
and collapses all cardinals in the interval
![]() $(\omega _1,\kappa )$
. Thus, if
$(\omega _1,\kappa )$
. Thus, if
![]() $\mathbb {P}^*$
does not preserve
$\mathbb {P}^*$
does not preserve
![]() $\kappa $
, then we may find a condition
$\kappa $
, then we may find a condition
![]() $p\in \mathbb {P}^*$
and a
$p\in \mathbb {P}^*$
and a
![]() $\mathbb {P}^*$
-name
$\mathbb {P}^*$
-name
![]() $\dot {f}$
for a function with domain
$\dot {f}$
for a function with domain
![]() $\omega _1$
which p forces is cofinal in
$\omega _1$
which p forces is cofinal in
![]() $\kappa $
. Since
$\kappa $
. Since
![]() $\mathbb {P}^*$
has size
$\mathbb {P}^*$
has size
![]() $\kappa $
, we may assume that the name
$\kappa $
, we may assume that the name
![]() $\dot {f}$
is a member of
$\dot {f}$
is a member of
![]() $H(\kappa ^+)$
. Let
$H(\kappa ^+)$
. Let
![]() $\vec {M}$
be an
$\vec {M}$
be an
![]() $\left \{\dot {f},p,\mathbb {P}^*\right \}$
-suitable sequence. Moreover, let
$\left \{\dot {f},p,\mathbb {P}^*\right \}$
-suitable sequence. Moreover, let
![]() $A\subseteq \operatorname {dom}(\vec {M})$
witness Definition 2.8, and let N denote the least model on the sequence
$A\subseteq \operatorname {dom}(\vec {M})$
witness Definition 2.8, and let N denote the least model on the sequence
![]() $\vec {M}\upharpoonright A$
. By Definition 2.8, we may find a condition
$\vec {M}\upharpoonright A$
. By Definition 2.8, we may find a condition
![]() $p^*(N)$
and an exact, strong residue function for
$p^*(N)$
and an exact, strong residue function for
![]() $(N,\mathbb {P}^*)$
above
$(N,\mathbb {P}^*)$
above
![]() $p^*(N)$
. Since
$p^*(N)$
. Since
![]() $p\in N$
, Definition 2.8(1) implies that
$p\in N$
, Definition 2.8(1) implies that
![]() $p^*(N)$
and p are compatible. So let q be an extension of them both. Then, since q is an
$p^*(N)$
and p are compatible. So let q be an extension of them both. Then, since q is an
![]() $(N,\mathbb {P}^*)$
-strongly generic condition and
$(N,\mathbb {P}^*)$
-strongly generic condition and
![]() $\dot {f}\in N$
, q forces that
$\dot {f}\in N$
, q forces that
![]() $\operatorname {ran}(\dot {f})\subseteq N\cap \kappa <\kappa $
. However, this contradicts the fact that p forces that
$\operatorname {ran}(\dot {f})\subseteq N\cap \kappa <\kappa $
. However, this contradicts the fact that p forces that
![]() $\dot {f}$
is unbounded in
$\dot {f}$
is unbounded in
![]() $\kappa $
.▪
$\kappa $
.▪
The remainder of the subsection is dedicated to proving lemmas about how suitable sequences interact with the weak compactness of
![]() $\kappa $
.
$\kappa $
.
Lemma 2.10 Let
![]() $P\in H(\kappa ^+)$
, and let
$P\in H(\kappa ^+)$
, and let
![]() $\vec {M}$
be P-suitable. Then
$\vec {M}$
be P-suitable. Then
![]() $P\subseteq \bigcup _{\alpha \in \operatorname {dom}(\vec {M})}M_\alpha $
.
$P\subseteq \bigcup _{\alpha \in \operatorname {dom}(\vec {M})}M_\alpha $
.
Proof By definition of a suitable sequence, each model on the sequence is elementary with respect to the fixed well-order
![]() $\lhd $
on
$\lhd $
on
![]() $H(\kappa ^+)$
, and therefore each model contains the
$H(\kappa ^+)$
, and therefore each model contains the
![]() $\lhd $
-least surjection
$\lhd $
-least surjection
![]() $\psi $
from
$\psi $
from
![]() $\kappa $
onto P. Then
$\kappa $
onto P. Then
▪
Lemma 2.11 Let
![]() $P\in H(\kappa ^+)$
, and let
$P\in H(\kappa ^+)$
, and let
![]() $\vec {M}$
be P-suitable. Suppose that
$\vec {M}$
be P-suitable. Suppose that
![]() $M^*$
is a
$M^*$
is a
![]() $\kappa $
-model containing
$\kappa $
-model containing
![]() $\vec {M}$
and that U is an
$\vec {M}$
and that U is an
![]() $M^*$
-normal ultrafilter on
$M^*$
-normal ultrafilter on
![]() $\kappa $
so that
$\kappa $
so that
![]() $\operatorname {dom}(\vec {M})\in U$
. Let
$\operatorname {dom}(\vec {M})\in U$
. Let
![]() $j:M^*\longrightarrow N$
be the ultrapower embedding. Then:
$j:M^*\longrightarrow N$
be the ultrapower embedding. Then:
-
(1)
 $\kappa \in \operatorname {dom}(j(\vec {M}))$
, and
$\kappa \in \operatorname {dom}(j(\vec {M}))$
, and
 $j(\vec {M})(\kappa )=\bigcup _{\alpha \in \operatorname {dom}(\vec {M})}j[M_\alpha ]$
;
$j(\vec {M})(\kappa )=\bigcup _{\alpha \in \operatorname {dom}(\vec {M})}j[M_\alpha ]$
; -
(2)
 $j(P)\cap j(\vec {M})(\kappa )=j[P];$
and
$j(P)\cap j(\vec {M})(\kappa )=j[P];$
and -
(3)
 $\bigcup _{\alpha \in \operatorname {dom}(\vec {M})}M_\alpha $
is transitive, and
$\bigcup _{\alpha \in \operatorname {dom}(\vec {M})}M_\alpha $
is transitive, and
 $j^{-1}\upharpoonright M_\kappa $
is the transitive collapse of
$j^{-1}\upharpoonright M_\kappa $
is the transitive collapse of
 $M_\kappa $
.
$M_\kappa $
.
Proof Let
![]() $B:=\operatorname {dom}(\vec {M})$
. The first part of item (1) follows since
$B:=\operatorname {dom}(\vec {M})$
. The first part of item (1) follows since
![]() $B\in U=\left \{ X\in \mathcal {P}(\kappa )\cap M^*:\kappa \in j(X)\right \}$
. Thus,
$B\in U=\left \{ X\in \mathcal {P}(\kappa )\cap M^*:\kappa \in j(X)\right \}$
. Thus,
![]() $\kappa \in \operatorname {dom}(j(\vec {M}))$
, and so we may let
$\kappa \in \operatorname {dom}(j(\vec {M}))$
, and so we may let
![]() $M_\kappa :=j(\vec {M})(\kappa )$
. In addition,
$M_\kappa :=j(\vec {M})(\kappa )$
. In addition,
![]() $j(B)\cap \kappa =B$
, and so by Definition 2.7(4),
$j(B)\cap \kappa =B$
, and so by Definition 2.7(4),
![]() $M_\kappa =\bigcup _{\alpha \in B}j(M_\alpha )$
. However,
$M_\kappa =\bigcup _{\alpha \in B}j(M_\alpha )$
. However,
![]() $|M_\alpha |=\alpha <\kappa $
for each
$|M_\alpha |=\alpha <\kappa $
for each
![]() $\alpha \in B$
, and hence
$\alpha \in B$
, and hence
![]() $j(M_\alpha )=j[M_\alpha ]$
. Thus,
$j(M_\alpha )=j[M_\alpha ]$
. Thus,
completing the proof of (1). (2) follows immediately.
For (3), observe that if
![]() $x\in M:=\bigcup _{\alpha \in \operatorname {dom}(\vec {M})}M_\alpha $
, then a tail of the sequence
$x\in M:=\bigcup _{\alpha \in \operatorname {dom}(\vec {M})}M_\alpha $
, then a tail of the sequence
![]() $\vec {M}$
is x-suitable, and so
$\vec {M}$
is x-suitable, and so
![]() $x\subseteq M$
by Lemma 2.10. Thus, M is transitive. Since
$x\subseteq M$
by Lemma 2.10. Thus, M is transitive. Since
![]() $j^{-1}\upharpoonright M_\kappa $
is an
$j^{-1}\upharpoonright M_\kappa $
is an
![]() $\in $
-isomorphism whose range (namely M) is transitive,
$\in $
-isomorphism whose range (namely M) is transitive,
![]() $j^{-1}$
is the transitive collapse.▪
$j^{-1}$
is the transitive collapse.▪
Lemma 2.12 Suppose that
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\mathbb {P}^*$
-suitable and that
$\mathbb {P}^*$
-suitable and that
![]() $\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in \operatorname {dom}(\vec {M})\rangle $
is a residue system for
$\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in \operatorname {dom}(\vec {M})\rangle $
is a residue system for
![]() $\vec {M}$
and
$\vec {M}$
and
![]() $\mathbb {P}^*$
. Then we may find some
$\mathbb {P}^*$
. Then we may find some
![]() $A\subseteq \operatorname {dom}(\vec {M})$
with
$A\subseteq \operatorname {dom}(\vec {M})$
with
![]() $\operatorname {dom}(\vec {M})\backslash A\in \mathcal {I}$
so that for all
$\operatorname {dom}(\vec {M})\backslash A\in \mathcal {I}$
so that for all
![]() $\alpha \in A$
,
$\alpha \in A$
,
![]() $\mathbb {P}^*\cap M_\alpha \Vdash \check {\alpha }=\dot {\aleph }_2$
.
$\mathbb {P}^*\cap M_\alpha \Vdash \check {\alpha }=\dot {\aleph }_2$
.
Proof Suppose that
![]() $\vec {M}$
and
$\vec {M}$
and
![]() $\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in \operatorname {dom}(\vec {M})\rangle $
are as in the statement of the lemma. For a contradiction, assume that
$\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in \operatorname {dom}(\vec {M})\rangle $
are as in the statement of the lemma. For a contradiction, assume that
Since
![]() $\mathcal {F}_{WC}\subseteq \mathcal {F}$
, B is also in
$\mathcal {F}_{WC}\subseteq \mathcal {F}$
, B is also in
![]() $\mathcal {F}_{WC}^+$
.
$\mathcal {F}_{WC}^+$
.
Let
![]() $M^*$
be a
$M^*$
be a
![]() $\kappa $
-model containing
$\kappa $
-model containing
![]() $\vec {M}$
, B,
$\vec {M}$
, B,
![]() $\mathbb {P}^*$
, and the sequence
$\mathbb {P}^*$
, and the sequence
![]() $\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in \operatorname {dom}(\vec {M})\rangle $
. By Proposition 1.4, since
$\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in \operatorname {dom}(\vec {M})\rangle $
. By Proposition 1.4, since
![]() $\kappa \backslash B\notin \mathcal {F}_{WC}$
, we may find some
$\kappa \backslash B\notin \mathcal {F}_{WC}$
, we may find some
![]() $M^*$
-normal measure U so that, letting
$M^*$
-normal measure U so that, letting
![]() $j:M^*\longrightarrow N$
be the associated ultrapower embedding,
$j:M^*\longrightarrow N$
be the associated ultrapower embedding,
![]() $\kappa \in j(B)$
. Let
$\kappa \in j(B)$
. Let
![]() $M_\kappa =j(\vec {M})(\kappa )$
. Then N satisfies that
$M_\kappa =j(\vec {M})(\kappa )$
. Then N satisfies that
![]() $j(\mathbb {P}^*)\cap M_\kappa $
does not force that
$j(\mathbb {P}^*)\cap M_\kappa $
does not force that
![]() $\check {\kappa }\,{=}\,\dot {\aleph }_2$
. On the other hand, by the previous lemma, we know that
$\check {\kappa }\,{=}\,\dot {\aleph }_2$
. On the other hand, by the previous lemma, we know that
![]() $j(\mathbb {P}^*)\cap M_\kappa =j[\mathbb {P}^*]$
. Since
$j(\mathbb {P}^*)\cap M_\kappa =j[\mathbb {P}^*]$
. Since
![]() $j[\mathbb {P}^*]$
is isomorphic to
$j[\mathbb {P}^*]$
is isomorphic to
![]() $\mathbb {P}^*$
and
$\mathbb {P}^*$
and
![]() $\mathbb {P}^*$
forces that
$\mathbb {P}^*$
forces that
![]() $\kappa $
becomes
$\kappa $
becomes
![]() $\aleph _2$
(by Lemma 2.9), this implies that
$\aleph _2$
(by Lemma 2.9), this implies that
![]() $j[\mathbb {P}^*]$
forces that
$j[\mathbb {P}^*]$
forces that
![]() $\kappa =\dot {\aleph }_2$
. Thus, N also satisfies that
$\kappa =\dot {\aleph }_2$
. Thus, N also satisfies that
![]() $j[\mathbb {P}^*]=j(\mathbb {P}^*)\cap M_\kappa $
forces that
$j[\mathbb {P}^*]=j(\mathbb {P}^*)\cap M_\kappa $
forces that
![]() $\check {\kappa }=\dot {\aleph }_2$
, a contradiction.▪
$\check {\kappa }=\dot {\aleph }_2$
, a contradiction.▪
We recall that in Definition 2.8(1), the condition
![]() $p^*(M_\alpha )$
is required to be compatible with every condition in
$p^*(M_\alpha )$
is required to be compatible with every condition in
![]() $\mathbb {P}^*\cap M_\alpha $
. A practical corollary of this is that any generic for
$\mathbb {P}^*\cap M_\alpha $
. A practical corollary of this is that any generic for
![]() $\mathbb {P}^*$
contains plenty of conditions of the form
$\mathbb {P}^*$
contains plenty of conditions of the form
![]() $p^*(M_\alpha )$
.
$p^*(M_\alpha )$
.
Lemma 2.13 Suppose that
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\mathbb {P}^*$
-suitable, that
$\mathbb {P}^*$
-suitable, that
![]() $ \langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in \operatorname {dom}(\vec {M})\rangle $
is a residue system for
$ \langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in \operatorname {dom}(\vec {M})\rangle $
is a residue system for
![]() $\vec {M}$
and
$\vec {M}$
and
![]() $\mathbb {P}^*$
, and that
$\mathbb {P}^*$
, and that
![]() $B\subseteq \operatorname {dom}(\vec {M})$
is in
$B\subseteq \operatorname {dom}(\vec {M})$
is in
![]() $\mathcal {F}^+$
. Suppose that there is a condition
$\mathcal {F}^+$
. Suppose that there is a condition
![]() $\bar {p}\in \mathbb {P}^*$
satisfying that for each
$\bar {p}\in \mathbb {P}^*$
satisfying that for each
![]() $\alpha \in B$
, there is a condition
$\alpha \in B$
, there is a condition
![]() $p_\alpha \in \operatorname {dom}(\varphi ^{M_\alpha })$
so that
$p_\alpha \in \operatorname {dom}(\varphi ^{M_\alpha })$
so that
![]() $\bar {p}=^*\varphi ^{M_\alpha }(p_\alpha )$
. Then
$\bar {p}=^*\varphi ^{M_\alpha }(p_\alpha )$
. Then
In particular, taking
![]() $p_\alpha :=p^*(M_\alpha )$
with
$p_\alpha :=p^*(M_\alpha )$
with
![]() $\bar {p}$
the trivial condition, and recalling Definition 2.8(1),
$\bar {p}$
the trivial condition, and recalling Definition 2.8(1),
Moreover, letting E abbreviate
![]() $\operatorname {dom}(\vec {M})$
, if
$\operatorname {dom}(\vec {M})$
, if
![]() $\alpha \in E\cap \lim (E)$
, then
$\alpha \in E\cap \lim (E)$
, then
Proof Let
![]() $p\in \mathbb {P}^*$
be a condition extending
$p\in \mathbb {P}^*$
be a condition extending
![]() $\bar {p}$
, and let
$\bar {p}$
, and let
![]() $\gamma <\kappa $
. We find an extension of p which forces that
$\gamma <\kappa $
. We find an extension of p which forces that
![]() $\dot {X}\backslash \gamma \neq \emptyset $
. Since B is unbounded in
$\dot {X}\backslash \gamma \neq \emptyset $
. Since B is unbounded in
![]() $\kappa $
and
$\kappa $
and
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\mathbb {P}^*$
-suitable, Lemma 2.10 implies that
$\mathbb {P}^*$
-suitable, Lemma 2.10 implies that
![]() $p\in M_\beta $
for some
$p\in M_\beta $
for some
![]() $\beta \in B\backslash (\gamma +1)$
. By definition of an exact, strong residue function,
$\beta \in B\backslash (\gamma +1)$
. By definition of an exact, strong residue function,
![]() $p_\beta $
is compatible with
$p_\beta $
is compatible with
![]() $p\geq \bar {p}=^*\varphi ^{M_\beta }(p_\beta )$
. Therefore, let
$p\geq \bar {p}=^*\varphi ^{M_\beta }(p_\beta )$
. Therefore, let
![]() $p^*$
be a common extension; then
$p^*$
be a common extension; then
![]() $p^*\Vdash \beta \in \dot {X}\backslash \gamma $
.
$p^*\Vdash \beta \in \dot {X}\backslash \gamma $
.
The proof in the case
![]() $\alpha \in E\cap \lim (E)$
is identical, using the fact that, by Definition 2.7,
$\alpha \in E\cap \lim (E)$
is identical, using the fact that, by Definition 2.7,
![]() $M_\alpha =\bigcup _{\xi \in B\cap \alpha }M_\xi $
in this case.▪
$M_\alpha =\bigcup _{\xi \in B\cap \alpha }M_\xi $
in this case.▪
3
 $\mathcal {F}$
-strongly proper posets and specializing Aronszajn trees on
$\mathcal {F}$
-strongly proper posets and specializing Aronszajn trees on
 $\omega _2$
$\omega _2$
In this section, we will prove that if
![]() $\mathbb {P}^*$
is an
$\mathbb {P}^*$
is an
![]() $\mathcal {F}$
-strongly proper poset, then we can iterate to specialize Aronszajn trees on
$\mathcal {F}$
-strongly proper poset, then we can iterate to specialize Aronszajn trees on
![]() $\kappa $
in the extension by
$\kappa $
in the extension by
![]() $\mathbb {P}^*$
(see Definition 2.8 for the definition of
$\mathbb {P}^*$
(see Definition 2.8 for the definition of
![]() $\mathcal {F}$
). Recall from Lemma 2.9 that
$\mathcal {F}$
). Recall from Lemma 2.9 that
![]() $\mathbb {P}^*$
forces that
$\mathbb {P}^*$
forces that
![]() $\kappa $
becomes
$\kappa $
becomes
![]() $\aleph _2$
and also preserves the
$\aleph _2$
and also preserves the
![]() $\mathsf {CH}$
; thus, there are in fact Aronszajn trees on
$\mathsf {CH}$
; thus, there are in fact Aronszajn trees on
![]() $\kappa $
in any
$\kappa $
in any
![]() $\mathbb {P}^*$
-extension. By Example 2.8, the collapse poset
$\mathbb {P}^*$
-extension. By Example 2.8, the collapse poset
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\mathcal {F}$
-strongly proper, and therefore, in the case that
$\mathcal {F}$
-strongly proper, and therefore, in the case that
![]() $\mathbb {P}^*=\mathbb {P}$
, our results here generalize those of [Reference Laver and Shelah30] (recall that
$\mathbb {P}^*=\mathbb {P}$
, our results here generalize those of [Reference Laver and Shelah30] (recall that
![]() $\mathcal {F}=\mathcal {F}_{WC}$
when
$\mathcal {F}=\mathcal {F}_{WC}$
when
![]() $\mathbb {P}^*=\mathbb {P}$
).
$\mathbb {P}^*=\mathbb {P}$
).
We consider a countable support iteration
![]() $\dot {\mathbb {S}} = \langle \dot {\mathbb {S}}_\xi , \dot {\mathbb {S}}(\xi ) : \xi < \kappa ^+\rangle $
of length
$\dot {\mathbb {S}} = \langle \dot {\mathbb {S}}_\xi , \dot {\mathbb {S}}(\xi ) : \xi < \kappa ^+\rangle $
of length
![]() $\kappa ^+$
, specializing Aronszajn trees on
$\kappa ^+$
, specializing Aronszajn trees on
![]() $\kappa $
in the
$\kappa $
in the
![]() $\mathbb {P}^*$
-extension. More precisely,
$\mathbb {P}^*$
-extension. More precisely,
![]() $\dot {\mathbb {S}}$
is a
$\dot {\mathbb {S}}$
is a
![]() $\mathbb {P}^*$
-name for an iteration with countable support so that for any
$\mathbb {P}^*$
-name for an iteration with countable support so that for any
![]() $\xi <\kappa ^+$
,
$\xi <\kappa ^+$
,
![]() $\dot {\mathbb {S}}(\xi )$
is an
$\dot {\mathbb {S}}(\xi )$
is an
![]() $\dot {\mathbb {S}}_\xi $
-name for the poset
$\dot {\mathbb {S}}_\xi $
-name for the poset
![]() $\dot {\mathbb {S}}(\dot {T}_\xi )$
, where
$\dot {\mathbb {S}}(\dot {T}_\xi )$
, where
![]() $\dot {T}_\xi $
is a nice
$\dot {T}_\xi $
is a nice
![]() $\dot {\mathbb {S}}_\xi $
-name for an Aronszajn tree on
$\dot {\mathbb {S}}_\xi $
-name for an Aronszajn tree on
![]() $\kappa $
(see Definition 1.4 for the exact definition of posets of the form
$\kappa $
(see Definition 1.4 for the exact definition of posets of the form
![]() $\mathbb {S}(T)$
). The selection of the names
$\mathbb {S}(T)$
). The selection of the names
![]() $\dot {T}_\xi $
—and hence the definition of the iteration—is determined by using the fixed well-order
$\dot {T}_\xi $
—and hence the definition of the iteration—is determined by using the fixed well-order
![]() $\lhd $
of
$\lhd $
of
![]() $H(\kappa ^+)$
from Notation 2.6 as a bookkeeping function. In particular, for each
$H(\kappa ^+)$
from Notation 2.6 as a bookkeeping function. In particular, for each
![]() $\xi <\kappa ^+$
, the name
$\xi <\kappa ^+$
, the name
![]() $\dot {\mathbb {S}}_\xi $
is definable in
$\dot {\mathbb {S}}_\xi $
is definable in
![]() $(H(\kappa ^+),\in ,\lhd )$
from
$(H(\kappa ^+),\in ,\lhd )$
from
![]() $\mathbb {P}^*$
and
$\mathbb {P}^*$
and
![]() $\xi $
, and consequently it is a member of any model which is suitable with respect to
$\xi $
, and consequently it is a member of any model which is suitable with respect to
![]() $\mathbb {P}^*$
and
$\mathbb {P}^*$
and
![]() $\xi $
. We will use
$\xi $
. We will use
![]() $\mathbb {R}_\xi $
to abbreviate
$\mathbb {R}_\xi $
to abbreviate
![]() $\mathbb {P}^*\ast \dot {\mathbb {S}}_\xi $
for each
$\mathbb {P}^*\ast \dot {\mathbb {S}}_\xi $
for each
![]() $\xi < \kappa ^+$
.
$\xi < \kappa ^+$
.
Since the poset
![]() $\mathbb {R}_\xi $
is
$\mathbb {R}_\xi $
is
![]() $\omega _1$
-closed, it is straightforward to see that
$\omega _1$
-closed, it is straightforward to see that
![]() $\mathbb {R}_\xi $
has a dense set of determined conditions, i.e., conditions
$\mathbb {R}_\xi $
has a dense set of determined conditions, i.e., conditions
![]() $(p,\dot {f})$
for which there is some function f in V so that
$(p,\dot {f})$
for which there is some function f in V so that
![]() $p\Vdash _{\mathbb {P}^*}\dot {f}=\check {f}$
. The dense set of determined conditions is also closed under sups of countable increasing sequences. Thus, we will assume that all future conditions are determined.
$p\Vdash _{\mathbb {P}^*}\dot {f}=\check {f}$
. The dense set of determined conditions is also closed under sups of countable increasing sequences. Thus, we will assume that all future conditions are determined.
Notation 3.1 Strictly speaking, the domain of a (determined) condition f in
![]() $\mathbb {R}_\xi $
is a countable subset of
$\mathbb {R}_\xi $
is a countable subset of
![]() $\xi $
, and for each
$\xi $
, and for each
![]() $\zeta \in \operatorname {dom}(f)$
,
$\zeta \in \operatorname {dom}(f)$
,
![]() $f(\zeta )$
is itself a function whose domain is a countable subset of
$f(\zeta )$
is itself a function whose domain is a countable subset of
![]() $\omega _1$
. However, we will often make an abuse of notation and write
$\omega _1$
. However, we will often make an abuse of notation and write
![]() $f(\zeta ,\nu )$
to mean the countable set of tree nodes
$f(\zeta ,\nu )$
to mean the countable set of tree nodes
![]() $f(\zeta )(\nu )$
.
$f(\zeta )(\nu )$
.
The main goal of this section is to prove that
![]() $\dot {\mathbb {S}}$
is forced to be
$\dot {\mathbb {S}}$
is forced to be
![]() $\kappa $
-c.c. For this, it suffices to prove the following.
$\kappa $
-c.c. For this, it suffices to prove the following.
Theorem 3.1 For every
![]() $\rho <\kappa ^+$
, it is forced by the trivial condition of
$\rho <\kappa ^+$
, it is forced by the trivial condition of
![]() $\mathbb {P}^*$
that
$\mathbb {P}^*$
that
![]() $\dot {\mathbb {S}}_\rho $
is
$\dot {\mathbb {S}}_\rho $
is
![]() $\kappa $
-c.c.
$\kappa $
-c.c.
We will prove Theorem 3.1 by induction on
![]() $\rho $
. Doing so will require two induction hypotheses, the first of which is the following.
$\rho $
. Doing so will require two induction hypotheses, the first of which is the following.
Inductive Hypothesis I: For each
![]() $\xi <\rho $
,
$\xi <\rho $
,
![]() $\mathbb {P}^*\Vdash \dot {\mathbb {S}}_\xi $
is
$\mathbb {P}^*\Vdash \dot {\mathbb {S}}_\xi $
is
![]() $\kappa $
-c.c.
$\kappa $
-c.c.
We will assume Inductive Hypothesis I throughout the entire section. Later in the section, after developing more of the theory, we will introduce a second, more technical inductive hypothesis; we state this after Remark 3.6. Although we assume the first inductive hypothesis throughout, we will only use the second inductive hypothesis once it is introduced, and the results prior to the statement thereof do not require it.
The rest of the section will proceed as follows. We will first establish, in Proposition 3.2, that for all
![]() $\xi <\rho $
, there are plenty of intermediate generic extensions between V and the full
$\xi <\rho $
, there are plenty of intermediate generic extensions between V and the full
![]() $\mathbb {R}_\xi $
-extension in which various restrictions of Aronszajn trees are Aronszajn in the intermediate model. In light of this, we will define analogues of the “hashtag” and “star” principles from [Reference Laver and Shelah30]; the former will say that two conditions have the same restriction to a given model, whereas the latter says that two conditions have a dual residue to a given model. Afterward, we define the notion of a splitting pair of conditions, a notion which will play a key role in later amalgamation arguments. Next, we will state our second induction hypothesis, which describes the interplay between the star and hashtag principles. Using the second induction hypothesis, we will prove that splitting pairs exist and isolate sufficient conditions under which they can be amalgamated (see Lemma 3.8). Finally, we show that
$\mathbb {R}_\xi $
-extension in which various restrictions of Aronszajn trees are Aronszajn in the intermediate model. In light of this, we will define analogues of the “hashtag” and “star” principles from [Reference Laver and Shelah30]; the former will say that two conditions have the same restriction to a given model, whereas the latter says that two conditions have a dual residue to a given model. Afterward, we define the notion of a splitting pair of conditions, a notion which will play a key role in later amalgamation arguments. Next, we will state our second induction hypothesis, which describes the interplay between the star and hashtag principles. Using the second induction hypothesis, we will prove that splitting pairs exist and isolate sufficient conditions under which they can be amalgamated (see Lemma 3.8). Finally, we show that
![]() $\dot {\mathbb {S}}_\rho $
is forced to be
$\dot {\mathbb {S}}_\rho $
is forced to be
![]() $\kappa $
-c.c., and we verify that the second induction hypothesis holds at
$\kappa $
-c.c., and we verify that the second induction hypothesis holds at
![]() $\rho $
. As mentioned in Remark 1.6(1), the only substantial use of the ineffability of
$\rho $
. As mentioned in Remark 1.6(1), the only substantial use of the ineffability of
![]() $\kappa $
is in verifying that the second induction hypothesis holds at
$\kappa $
is in verifying that the second induction hypothesis holds at
![]() $\kappa $
.
$\kappa $
.
Definition 3.2 Let
![]() $G^*$
be V-generic over
$G^*$
be V-generic over
![]() $\mathbb {P}^*$
. If
$\mathbb {P}^*$
. If
![]() $\xi \leq \rho $
,
$\xi \leq \rho $
,
![]() $f\in \mathbb {S}_\xi $
, and
$f\in \mathbb {S}_\xi $
, and
![]() $\bar {f}$
is a function (not necessarily a condition), we write
$\bar {f}$
is a function (not necessarily a condition), we write
![]() $f\geq \bar {f}$
to mean that
$f\geq \bar {f}$
to mean that
![]() $\operatorname {dom}(\bar {f})\subseteq \operatorname {dom}(f)$
and for all
$\operatorname {dom}(\bar {f})\subseteq \operatorname {dom}(f)$
and for all
![]() $\langle \zeta ,\nu \rangle \in \operatorname {dom}(\bar {f})$
,
$\langle \zeta ,\nu \rangle \in \operatorname {dom}(\bar {f})$
,
![]() $\bar {f}(\zeta ,\nu )\subseteq f(\zeta ,\nu )$
.
$\bar {f}(\zeta ,\nu )\subseteq f(\zeta ,\nu )$
.
The next item establishes the existence of the desired intermediate generic extensions between V and
![]() $V[\mathbb {R}_\xi ]$
for
$V[\mathbb {R}_\xi ]$
for
![]() $\xi <\rho $
, and in turn the existence of plenty of residues. We recommend recalling Lemma 2.11 and Notation 1.7 before reading the proof. In the statement of the following proposition, we will assume that the various names are nice names for subsets of
$\xi <\rho $
, and in turn the existence of plenty of residues. We recommend recalling Lemma 2.11 and Notation 1.7 before reading the proof. In the statement of the following proposition, we will assume that the various names are nice names for subsets of
![]() $H(\kappa ^+)$
. Thus, in light of our discussion about determined conditions, the name
$H(\kappa ^+)$
. Thus, in light of our discussion about determined conditions, the name
![]() $\dot {\mathbb {S}}_\zeta $
will be viewed as a union of sets of the form
$\dot {\mathbb {S}}_\zeta $
will be viewed as a union of sets of the form
![]() $\left \{ f\right \}\times A_f$
, where
$\left \{ f\right \}\times A_f$
, where
![]() $f:\zeta \times \omega _1\rightharpoonup \kappa \times \omega _1$
is a countable partial function and
$f:\zeta \times \omega _1\rightharpoonup \kappa \times \omega _1$
is a countable partial function and
![]() $A_f\subseteq \mathbb {P}^*$
is an antichain. This will ensure, for instance, that
$A_f\subseteq \mathbb {P}^*$
is an antichain. This will ensure, for instance, that
![]() $\dot {\mathbb {S}}_\zeta \cap M_\alpha $
is really a
$\dot {\mathbb {S}}_\zeta \cap M_\alpha $
is really a
![]() $(\mathbb {P}^*\cap M_\alpha )$
-name. Similar considerations apply to the
$(\mathbb {P}^*\cap M_\alpha )$
-name. Similar considerations apply to the
![]() $\mathbb {R}_\zeta $
-name
$\mathbb {R}_\zeta $
-name
![]() $\dot {T}_\zeta $
.
$\dot {T}_\zeta $
.
Proposition 3.2 Suppose that
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\mathbb {R}_\rho $
-suitable. Then there exists
$\mathbb {R}_\rho $
-suitable. Then there exists
![]() $B^*\subseteq \operatorname {dom}(\vec {M})$
with
$B^*\subseteq \operatorname {dom}(\vec {M})$
with
![]() $\operatorname {dom}(\vec {M})\backslash B^*\in \mathcal {I}$
so that for any
$\operatorname {dom}(\vec {M})\backslash B^*\in \mathcal {I}$
so that for any
![]() $\alpha \in B^*$
, for any residue pair
$\alpha \in B^*$
, for any residue pair
![]() $\langle p^*(M_\alpha ), \varphi ^{M_\alpha }\rangle $
for
$\langle p^*(M_\alpha ), \varphi ^{M_\alpha }\rangle $
for
![]() $(M_\alpha ,\mathbb {P}^*)$
, and for any
$(M_\alpha ,\mathbb {P}^*)$
, and for any
![]() $\zeta \in M_\alpha \cap \rho $
, the following are true:
$\zeta \in M_\alpha \cap \rho $
, the following are true:
-
(1)
 $(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
forces that
$(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
forces that
 $\dot {G}_{\mathbb {R}_\zeta }\cap {M_\alpha }$
is a V-generic filter for
$\dot {G}_{\mathbb {R}_\zeta }\cap {M_\alpha }$
is a V-generic filter for
 $\mathbb {R}_\zeta \cap M_\alpha $
;
$\mathbb {R}_\zeta \cap M_\alpha $
; -
(2)
 $(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
forces that
$(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
forces that
 $\dot {T}_\zeta \cap (\check {\omega }_1\times \check {\alpha })=(\dot {T}_\zeta \cap M_\alpha )[\dot {G}_{\mathbb {R}_\zeta }\cap M_\alpha ]$
; and
$\dot {T}_\zeta \cap (\check {\omega }_1\times \check {\alpha })=(\dot {T}_\zeta \cap M_\alpha )[\dot {G}_{\mathbb {R}_\zeta }\cap M_\alpha ]$
; and -
(3)
 $(\mathbb {P}^*\cap M_\alpha )\Vdash (\dot {\mathbb {S}}_\zeta \cap M_\alpha )$
is
$(\mathbb {P}^*\cap M_\alpha )\Vdash (\dot {\mathbb {S}}_\zeta \cap M_\alpha )$
is
 $\alpha $
-c.c. Furthermore,
$\alpha $
-c.c. Furthermore,
 $(\mathbb {R}_\zeta \cap M_\alpha )\Vdash \dot {T}_\zeta \cap {M_\alpha }$
is an Aronszajn tree on
$(\mathbb {R}_\zeta \cap M_\alpha )\Vdash \dot {T}_\zeta \cap {M_\alpha }$
is an Aronszajn tree on
 $\alpha =\dot {\aleph }_2$
.
$\alpha =\dot {\aleph }_2$
.
Proof Fix an
![]() $\mathbb {R}_\rho $
-suitable sequence
$\mathbb {R}_\rho $
-suitable sequence
![]() $\vec {M}$
, and let
$\vec {M}$
, and let
![]() $B:=\operatorname {dom}(\vec {M})$
so that
$B:=\operatorname {dom}(\vec {M})$
so that
![]() $B\in \mathcal {F}^+$
by Definition 2.7. Since
$B\in \mathcal {F}^+$
by Definition 2.7. Since
![]() $\mathbb {P}^*$
is
$\mathbb {P}^*$
is
![]() $\mathcal {F}$
-strongly proper, we may assume that B satisfies the conclusion of Definition 2.8, by removing an
$\mathcal {F}$
-strongly proper, we may assume that B satisfies the conclusion of Definition 2.8, by removing an
![]() $\mathcal {I}$
-null set if necessary. Our goal is to show that each of (1)–(3) fail only on a set in
$\mathcal {I}$
-null set if necessary. Our goal is to show that each of (1)–(3) fail only on a set in
![]() $\mathcal {I}$
. Thus, we define
$\mathcal {I}$
. Thus, we define
![]() $B_1$
to be the set of
$B_1$
to be the set of
![]() $\alpha \in B$
so that for some
$\alpha \in B$
so that for some
![]() $\zeta \in M_\alpha $
and some residue pair
$\zeta \in M_\alpha $
and some residue pair
![]() $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
, (1) fails for these objects; we define
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
, (1) fails for these objects; we define
![]() $B_2$
to be the set of
$B_2$
to be the set of
![]() $\alpha \in B$
so that for some
$\alpha \in B$
so that for some
![]() $\zeta \in M_\alpha \cap \rho $
and some residue pair
$\zeta \in M_\alpha \cap \rho $
and some residue pair
![]() $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
, (2) fails for
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
, (2) fails for
![]() $M_\alpha $
and
$M_\alpha $
and
![]() $\zeta $
; and we define
$\zeta $
; and we define
![]() $B_3$
similarly. We show that each of these is in
$B_3$
similarly. We show that each of these is in
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Suppose for a contradiction that
![]() $B_i\in \mathcal {F}^+$
for some
$B_i\in \mathcal {F}^+$
for some
![]() $i\in \left \{ 1,2,3\right \}$
. Then
$i\in \left \{ 1,2,3\right \}$
. Then
![]() $B_i\in \mathcal {F}_{WC}^+$
since
$B_i\in \mathcal {F}_{WC}^+$
since
![]() $\mathcal {F}_{WC}\subseteq \mathcal {F}$
. Let
$\mathcal {F}_{WC}\subseteq \mathcal {F}$
. Let
![]() $M^*$
be a
$M^*$
be a
![]() $\kappa $
model containing
$\kappa $
model containing
![]() $B_i$
as well as the sequence
$B_i$
as well as the sequence
![]() $\vec {M}$
. Applying Proposition 1.4, we may fix an
$\vec {M}$
. Applying Proposition 1.4, we may fix an
![]() $M^*$
-normal ultrafilter U containing
$M^*$
-normal ultrafilter U containing
![]() $B_i$
, and we let
$B_i$
, and we let
![]() $j:M^*\longrightarrow N$
be the induced ultrapower embedding. In particular,
$j:M^*\longrightarrow N$
be the induced ultrapower embedding. In particular,
![]() $\kappa \in j(B_i)$
.
$\kappa \in j(B_i)$
.
Let
![]() $M_\kappa :=j(\vec {M})(\kappa )$
. Fix
$M_\kappa :=j(\vec {M})(\kappa )$
. Fix
![]() $\zeta ^*\in M_\kappa \cap j(\rho )$
for the remainder of the proof which witnesses the relevant failure of (1), (2), or (3) on the j-side. Since
$\zeta ^*\in M_\kappa \cap j(\rho )$
for the remainder of the proof which witnesses the relevant failure of (1), (2), or (3) on the j-side. Since
![]() $M_\kappa =j\left [\bigcup _{\alpha \in B}M_\alpha \right ]$
, by Lemma 2.11, we have that
$M_\kappa =j\left [\bigcup _{\alpha \in B}M_\alpha \right ]$
, by Lemma 2.11, we have that
![]() $\zeta ^*\in \operatorname {ran}(j)$
, and so
$\zeta ^*\in \operatorname {ran}(j)$
, and so
![]() $\zeta ^*=j(\zeta )$
for some
$\zeta ^*=j(\zeta )$
for some
![]() $\zeta <\rho $
. Moreover,
$\zeta <\rho $
. Moreover,
![]() $M_\kappa \cap j(\mathbb {P}^*)=j[\mathbb {P}^*]$
.
$M_\kappa \cap j(\mathbb {P}^*)=j[\mathbb {P}^*]$
.
Case 1:
![]() $i=1$
. Since
$i=1$
. Since
![]() $\kappa \in j(B_1)$
, we may fix a residue pair
$\kappa \in j(B_1)$
, we may fix a residue pair
![]() $\langle p^*(M_\kappa ),\varphi ^{M_\kappa }\rangle $
for
$\langle p^*(M_\kappa ),\varphi ^{M_\kappa }\rangle $
for
![]() $(M_\kappa ,j(\mathbb {P}^*))$
so that
$(M_\kappa ,j(\mathbb {P}^*))$
so that
![]() $(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\zeta )})$
does not force that
$(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\zeta )})$
does not force that
![]() $\dot {G}_{j(\mathbb {R}_\zeta )}\cap M_\kappa $
is generic over
$\dot {G}_{j(\mathbb {R}_\zeta )}\cap M_\kappa $
is generic over
![]() $j(\mathbb {R}_\zeta )\cap M_\alpha $
.
$j(\mathbb {R}_\zeta )\cap M_\alpha $
.
To obtain our contradiction, we show that
![]() $(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\zeta )})$
in fact does force that
$(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\zeta )})$
in fact does force that
![]() $\dot {G}_{j(\mathbb {R}_\zeta )}\cap M_\kappa $
is generic over
$\dot {G}_{j(\mathbb {R}_\zeta )}\cap M_\kappa $
is generic over
![]() $j(\mathbb {R}_\zeta )\cap M_\kappa $
. Thus, fix an extension
$j(\mathbb {R}_\zeta )\cap M_\kappa $
. Thus, fix an extension
![]() $(q^*,\dot {g})$
of
$(q^*,\dot {g})$
of
![]() $(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\zeta )})$
in
$(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\zeta )})$
in
![]() $j(\mathbb {R}_\zeta )$
. Let
$j(\mathbb {R}_\zeta )$
. Let
![]() $A^*\in N$
be a maximal antichain of
$A^*\in N$
be a maximal antichain of
![]() $j(\mathbb {R}_\zeta )\cap M_\kappa =j[\mathbb {R}_\zeta ]$
, and we will find some extension of
$j(\mathbb {R}_\zeta )\cap M_\kappa =j[\mathbb {R}_\zeta ]$
, and we will find some extension of
![]() $(q^*,\dot {g})$
which forces that
$(q^*,\dot {g})$
which forces that
![]() $A^*\cap \dot {G}_{j(\mathbb {R}_\zeta )}\neq \emptyset $
. Since
$A^*\cap \dot {G}_{j(\mathbb {R}_\zeta )}\neq \emptyset $
. Since
![]() $q^*$
extends
$q^*$
extends
![]() $p^*(M_\kappa )$
in
$p^*(M_\kappa )$
in
![]() $j(\mathbb {P}^*)$
and
$j(\mathbb {P}^*)$
and
![]() $\varphi ^{M_\kappa }$
is an exact, strong residue function, we may extend and relabel, if necessary, to assume that
$\varphi ^{M_\kappa }$
is an exact, strong residue function, we may extend and relabel, if necessary, to assume that
![]() $q^*\in \operatorname {dom}(\varphi ^{M_\kappa })$
. Then
$q^*\in \operatorname {dom}(\varphi ^{M_\kappa })$
. Then
![]() $\varphi ^{M_\kappa }(q^*)\in j(\mathbb {P}^*)\cap M_\kappa =j[\mathbb {P}^*]$
. Therefore,
$\varphi ^{M_\kappa }(q^*)\in j(\mathbb {P}^*)\cap M_\kappa =j[\mathbb {P}^*]$
. Therefore,
![]() $\varphi ^{M_\kappa }(q^*)=j(q)$
for some
$\varphi ^{M_\kappa }(q^*)=j(q)$
for some
![]() $q\in \mathbb {P}^*$
.
$q\in \mathbb {P}^*$
.
Now, let
![]() $A:=j^{-1}[A^*]$
; since
$A:=j^{-1}[A^*]$
; since
![]() $A^*$
is a maximal antichain in
$A^*$
is a maximal antichain in
![]() $j[\mathbb {R}_\zeta ]$
, A is a maximal antichain in
$j[\mathbb {R}_\zeta ]$
, A is a maximal antichain in
![]() $\mathbb {R}_\zeta $
. However, note that since
$\mathbb {R}_\zeta $
. However, note that since
![]() $\mathbb {R}_\zeta $
is not necessarily
$\mathbb {R}_\zeta $
is not necessarily
![]() $\kappa $
-c.c., A could very well have size
$\kappa $
-c.c., A could very well have size
![]() $\kappa $
, and therefore we cannot assume that it is an element of
$\kappa $
, and therefore we cannot assume that it is an element of
![]() $M^*$
. Until after the proof of the next claim, we will work in V, not
$M^*$
. Until after the proof of the next claim, we will work in V, not
![]() $M^*$
. Let
$M^*$
. Let
![]() $\dot {A}(1)$
be the
$\dot {A}(1)$
be the
![]() $\mathbb {P}^*$
-name for
$\mathbb {P}^*$
-name for
![]() $ \left \{ f\in \dot {\mathbb {S}}_\zeta :(\exists p\in \dot {G}_{\mathbb {P}^*})\;\;(p,f)\in A\right \}. $
Then
$ \left \{ f\in \dot {\mathbb {S}}_\zeta :(\exists p\in \dot {G}_{\mathbb {P}^*})\;\;(p,f)\in A\right \}. $
Then
![]() $q\Vdash \dot {A}(1)$
is a maximal antichain in
$q\Vdash \dot {A}(1)$
is a maximal antichain in
![]() $\dot {\mathbb {S}}_\zeta $
.
$\dot {\mathbb {S}}_\zeta $
.
Since
![]() $\mathbb {P}^*\Vdash \dot {\mathbb {S}}_\zeta $
is
$\mathbb {P}^*\Vdash \dot {\mathbb {S}}_\zeta $
is
![]() $\kappa $
-c.c., by Inductive Hypothesis I, we may extend q in
$\kappa $
-c.c., by Inductive Hypothesis I, we may extend q in
![]() $\mathbb {P}^*$
to some condition
$\mathbb {P}^*$
to some condition
![]() $q'$
and find an ordinal
$q'$
and find an ordinal
![]() $\beta <\kappa $
and a sequence
$\beta <\kappa $
and a sequence
![]() $\langle \dot {f}_\gamma :\gamma <\beta \rangle $
of
$\langle \dot {f}_\gamma :\gamma <\beta \rangle $
of
![]() $\mathbb {P}^*$
-names so that
$\mathbb {P}^*$
-names so that
Since a given
![]() $\dot {f}_\gamma $
need not be a member of
$\dot {f}_\gamma $
need not be a member of
![]() $M^*$
, we show how to replace these names with ones that are in
$M^*$
, we show how to replace these names with ones that are in
![]() $M^*$
, up to extending
$M^*$
, up to extending
![]() $q'$
.
$q'$
.
Claim 3.3 There exist a condition
![]() $u\geq _{\mathbb {P}^*}q'$
and a sequence of
$u\geq _{\mathbb {P}^*}q'$
and a sequence of
![]() $\mathbb {P}^*$
-names
$\mathbb {P}^*$
-names
![]() $\langle \dot {h}_\gamma :\gamma <\beta \rangle $
in
$\langle \dot {h}_\gamma :\gamma <\beta \rangle $
in
![]() $M^*$
so that
$M^*$
so that
![]() $u\Vdash ^V(\forall \gamma <\beta )\,\dot {h}_\gamma =\dot {f}_\gamma $
.▪
$u\Vdash ^V(\forall \gamma <\beta )\,\dot {h}_\gamma =\dot {f}_\gamma $
.▪
Proof To find u, let
![]() $G^*$
be a V-generic filter over
$G^*$
be a V-generic filter over
![]() $\mathbb {P}^*$
containing
$\mathbb {P}^*$
containing
![]() $q'$
. Then
$q'$
. Then
![]() $\mathbb {S}_\zeta :=\dot {\mathbb {S}}_\zeta [G^*]\subseteq \bigcup _{\eta \in B}M_\eta [G^*]$
, since
$\mathbb {S}_\zeta :=\dot {\mathbb {S}}_\zeta [G^*]\subseteq \bigcup _{\eta \in B}M_\eta [G^*]$
, since
![]() $\mathbb {R}_\zeta \subseteq \bigcup _{\eta \in B}M_\eta $
. Since
$\mathbb {R}_\zeta \subseteq \bigcup _{\eta \in B}M_\eta $
. Since
![]() $\kappa =\aleph _2^{V[G^*]}$
and
$\kappa =\aleph _2^{V[G^*]}$
and
![]() $\beta <\kappa $
, there exists some
$\beta <\kappa $
, there exists some
![]() $\eta \in B$
so that for all
$\eta \in B$
so that for all
![]() $\gamma <\beta $
,
$\gamma <\beta $
,
![]() $\dot {f}_\gamma [G^*]\in M_\eta [G^*]$
. By Lemma 2.13, there exists a
$\dot {f}_\gamma [G^*]\in M_\eta [G^*]$
. By Lemma 2.13, there exists a
![]() $\delta \geq \eta $
so that
$\delta \geq \eta $
so that
![]() $p^*(M_\delta )\in G^*$
. Now, let
$p^*(M_\delta )\in G^*$
. Now, let
![]() $u\in G^*$
be an extension of
$u\in G^*$
be an extension of
![]() $p^*(M_\delta )$
and
$p^*(M_\delta )$
and
![]() $q'$
so that
$q'$
so that
![]() $u\Vdash (\forall \gamma <\beta )\,\dot {f}_\gamma \in M_\delta [\dot {G}_{\mathbb {P}^*}]$
.
$u\Vdash (\forall \gamma <\beta )\,\dot {f}_\gamma \in M_\delta [\dot {G}_{\mathbb {P}^*}]$
.
Back in V, we define new names
![]() $\dot {h}_\gamma $
for each
$\dot {h}_\gamma $
for each
![]() $\gamma <\beta $
; recalling Notation 3.1, we view conditions in
$\gamma <\beta $
; recalling Notation 3.1, we view conditions in
![]() $\dot {\mathbb {S}}_\zeta $
as having a domain which is a countable subset of
$\dot {\mathbb {S}}_\zeta $
as having a domain which is a countable subset of
![]() $\zeta \times \omega _1$
so that each element in the range is a countable subset of
$\zeta \times \omega _1$
so that each element in the range is a countable subset of
![]() $\kappa \times \omega _1$
.
$\kappa \times \omega _1$
.
For each
![]() $\gamma <\beta $
, each
$\gamma <\beta $
, each
![]() $\bar {\zeta }\in \zeta \cap M_\delta $
(an iteration stage), each
$\bar {\zeta }\in \zeta \cap M_\delta $
(an iteration stage), each
![]() $\nu <\omega _1$
(corresponding to the
$\nu <\omega _1$
(corresponding to the
![]() $\nu $
th tree antichain), and each
$\nu $
th tree antichain), and each
![]() $\theta \in \delta \times \omega _1$
(a node with height below
$\theta \in \delta \times \omega _1$
(a node with height below
![]() $\delta $
), let
$\delta $
), let
![]() $A(\gamma ,\bar {\zeta },\nu ,\theta )$
be a maximal antichain in
$A(\gamma ,\bar {\zeta },\nu ,\theta )$
be a maximal antichain in
![]() $\mathbb {P}^*\cap M_\delta $
of conditions p which decide whether or not
$\mathbb {P}^*\cap M_\delta $
of conditions p which decide whether or not
![]() $\theta $
is a member of
$\theta $
is a member of
![]() $\dot {f}_\gamma (\bar {\zeta },\nu )$
. Let
$\dot {f}_\gamma (\bar {\zeta },\nu )$
. Let
![]() $\dot {h}_\gamma $
be the
$\dot {h}_\gamma $
be the
![]() $\mathbb {P}^*$
-name which is interpreted in an arbitrary generic extension via some
$\mathbb {P}^*$
-name which is interpreted in an arbitrary generic extension via some
![]() $G^*$
as follows:
$G^*$
as follows:
![]() $\theta \in {h}_\gamma (\bar {\zeta },\nu )$
iff there is some
$\theta \in {h}_\gamma (\bar {\zeta },\nu )$
iff there is some
![]() $p\in A(\gamma ,\bar {\zeta },\nu ,\theta )\cap G^*$
which forces that
$p\in A(\gamma ,\bar {\zeta },\nu ,\theta )\cap G^*$
which forces that
![]() $\theta \in \dot {f}_\gamma (\bar {\zeta },\nu )$
. Otherwise,
$\theta \in \dot {f}_\gamma (\bar {\zeta },\nu )$
. Otherwise,
![]() $h_\gamma $
is undefined.
$h_\gamma $
is undefined.
We claim that
![]() $u\Vdash ^V(\forall \gamma <\beta )\,\dot {h}_\gamma =\dot {f}_\gamma $
. To see this, let
$u\Vdash ^V(\forall \gamma <\beta )\,\dot {h}_\gamma =\dot {f}_\gamma $
. To see this, let
![]() $G^*$
be a V-generic filter containing u. Fix
$G^*$
be a V-generic filter containing u. Fix
![]() $\bar {\zeta }<\zeta $
and
$\bar {\zeta }<\zeta $
and
![]() $\nu <\omega _1$
, and we verify that
$\nu <\omega _1$
, and we verify that
![]() $f_\gamma (\bar {\zeta },\nu )=h_\gamma (\bar {\zeta },\nu )$
. On the one hand, if
$f_\gamma (\bar {\zeta },\nu )=h_\gamma (\bar {\zeta },\nu )$
. On the one hand, if
![]() $\theta \in h_\gamma (\bar {\zeta },\nu )$
, then by definition
$\theta \in h_\gamma (\bar {\zeta },\nu )$
, then by definition
![]() $f_\gamma (\bar {\zeta },\nu )$
is defined and also contains the node
$f_\gamma (\bar {\zeta },\nu )$
is defined and also contains the node
![]() $\theta $
.
$\theta $
.
On the other hand, if
![]() $\tau \in f_\gamma (\bar {\zeta },\nu )$
is a node, then since
$\tau \in f_\gamma (\bar {\zeta },\nu )$
is a node, then since
![]() $f_\gamma \in M_\delta [G^*]$
has a countable domain,
$f_\gamma \in M_\delta [G^*]$
has a countable domain,
![]() $\bar {\zeta }\in M_\delta [G^*]$
, and since
$\bar {\zeta }\in M_\delta [G^*]$
, and since
![]() $f_\gamma (\bar {\zeta },\nu )\in M_\delta [G^*]$
is countable,
$f_\gamma (\bar {\zeta },\nu )\in M_\delta [G^*]$
is countable,
![]() $\tau \in M_\delta [G^*]$
too. However,
$\tau \in M_\delta [G^*]$
too. However,
![]() $M_\delta [G^*]\cap V=M_\delta $
, since
$M_\delta [G^*]\cap V=M_\delta $
, since
![]() $u\in G^*$
is a (strongly)
$u\in G^*$
is a (strongly)
![]() $(M_\delta ,\mathbb {P}^*)$
-generic condition (as it extends
$(M_\delta ,\mathbb {P}^*)$
-generic condition (as it extends
![]() $p^*(M_\delta )$
). Hence,
$p^*(M_\delta )$
). Hence,
![]() $\bar {\zeta },\tau \in M_\delta $
. Thus,
$\bar {\zeta },\tau \in M_\delta $
. Thus,
![]() $\bar {\zeta }\in M_\delta \cap \zeta $
and
$\bar {\zeta }\in M_\delta \cap \zeta $
and
![]() $\tau $
has height below
$\tau $
has height below
![]() $M_\delta \cap \kappa =\delta $
. Next, since u is a strongly
$M_\delta \cap \kappa =\delta $
. Next, since u is a strongly
![]() $(M_\delta ,\mathbb {P}^*)$
-generic condition which is in
$(M_\delta ,\mathbb {P}^*)$
-generic condition which is in
![]() $G^*$
, and since
$G^*$
, and since
![]() $A(\gamma ,\bar {\zeta },\nu ,\tau )$
is a maximal antichain
$A(\gamma ,\bar {\zeta },\nu ,\tau )$
is a maximal antichain
![]() $\mathbb {P}^*\cap M_\delta $
, we know that
$\mathbb {P}^*\cap M_\delta $
, we know that
![]() $A(\gamma ,\bar {\zeta },\nu ,\tau )\cap G^*\neq \emptyset $
, say with
$A(\gamma ,\bar {\zeta },\nu ,\tau )\cap G^*\neq \emptyset $
, say with
![]() $\bar {u}$
in the intersection. However, as
$\bar {u}$
in the intersection. However, as
![]() $\tau \in f_\gamma (\bar {\zeta },\nu )$
, we must have that
$\tau \in f_\gamma (\bar {\zeta },\nu )$
, we must have that
![]() $\bar {u}$
forces that
$\bar {u}$
forces that
![]() $\tau \in \dot {f}_\gamma (\bar {\zeta },\nu )$
, and hence
$\tau \in \dot {f}_\gamma (\bar {\zeta },\nu )$
, and hence
![]() $\tau \in h_\gamma (\bar {\zeta },\nu )$
. This completes the proof that
$\tau \in h_\gamma (\bar {\zeta },\nu )$
. This completes the proof that
![]() $u\Vdash \dot {f}_\gamma =\dot {h}_\gamma $
for each
$u\Vdash \dot {f}_\gamma =\dot {h}_\gamma $
for each
![]() $\gamma <\beta $
.
$\gamma <\beta $
.
Finally, since
![]() $M^*$
is
$M^*$
is
![]() $< \kappa $
-closed, the sequence of antichains
$< \kappa $
-closed, the sequence of antichains
is a member of
![]() $M^*$
. Therefore, the sequence
$M^*$
. Therefore, the sequence
![]() $\langle \dot {h}_\gamma :\gamma <\beta \rangle $
is a member of
$\langle \dot {h}_\gamma :\gamma <\beta \rangle $
is a member of
![]() $M^*$
too.▪(Claim 3.3)
$M^*$
too.▪(Claim 3.3)
Continuing with the main body of the argument, let
![]() $u\geq _{\mathbb {P}^*}q'$
and
$u\geq _{\mathbb {P}^*}q'$
and
![]() $\langle \dot {h}_\gamma :\gamma <\beta \rangle $
witness the above claim. Since
$\langle \dot {h}_\gamma :\gamma <\beta \rangle $
witness the above claim. Since
![]() $q'\Vdash _{\mathbb {P}^*}\dot {A}(1)=\left \{\dot {f}_\gamma :\gamma <\beta \right \}$
and
$q'\Vdash _{\mathbb {P}^*}\dot {A}(1)=\left \{\dot {f}_\gamma :\gamma <\beta \right \}$
and
![]() $u\geq q'$
, we have
$u\geq q'$
, we have
Since
![]() $\langle \dot {h}_\gamma :\gamma <\beta \rangle $
and u are in
$\langle \dot {h}_\gamma :\gamma <\beta \rangle $
and u are in
![]() $M^*$
,
$M^*$
,
![]() $(*)$
is satisfied in
$(*)$
is satisfied in
![]() $M^*$
. Applying j,
$M^*$
. Applying j,
Next,
![]() $u\geq _{\mathbb {P}^*}q'\geq _{\mathbb {P}^*} q$
so
$u\geq _{\mathbb {P}^*}q'\geq _{\mathbb {P}^*} q$
so
![]() $j(u)\geq _{j(\mathbb {P}^*)} j(q)=\varphi ^{M_\kappa }(q^*)$
, and
$j(u)\geq _{j(\mathbb {P}^*)} j(q)=\varphi ^{M_\kappa }(q^*)$
, and
![]() $j(u)\in j[\mathbb {P}^*]\subseteq M_\kappa $
, so
$j(u)\in j[\mathbb {P}^*]\subseteq M_\kappa $
, so
![]() $j(u)$
and
$j(u)$
and
![]() $q^*$
are compatible in
$q^*$
are compatible in
![]() $j(\mathbb {P}^*)$
. Let
$j(\mathbb {P}^*)$
. Let
![]() $q^{**}$
be a condition extending both of them with
$q^{**}$
be a condition extending both of them with
![]() $\varphi ^{M_\kappa }(q^{**})\geq j(u)$
. Since
$\varphi ^{M_\kappa }(q^{**})\geq j(u)$
. Since
![]() $q^{**}$
extends
$q^{**}$
extends
![]() $q^*$
, which forces that
$q^*$
, which forces that
![]() $\dot {g}$
is a condition in
$\dot {g}$
is a condition in
![]() $j(\dot {\mathbb {S}}_\zeta )$
,
$j(\dot {\mathbb {S}}_\zeta )$
,
![]() $q^{**}$
forces this too. As
$q^{**}$
forces this too. As
![]() $q^{**}\geq j(u)$
also forces that
$q^{**}\geq j(u)$
also forces that
![]() $\left \{ j(\dot {h}_\gamma ):\gamma <\beta \right \}$
is a maximal antichain in
$\left \{ j(\dot {h}_\gamma ):\gamma <\beta \right \}$
is a maximal antichain in
![]() $j(\dot {\mathbb {S}}_\zeta )$
, we may find an extension
$j(\dot {\mathbb {S}}_\zeta )$
, we may find an extension
![]() $r^*$
of
$r^*$
of
![]() $q^{**}$
, a
$q^{**}$
, a
![]() $j(\mathbb {P}^*)$
-name
$j(\mathbb {P}^*)$
-name
![]() $\dot {g}^*$
, and an ordinal
$\dot {g}^*$
, and an ordinal
![]() $\gamma <\beta $
so that
$\gamma <\beta $
so that
We may also extend, if necessary, to assume that
![]() $r^*\in \operatorname {dom}(\varphi ^{M_\kappa })$
, since
$r^*\in \operatorname {dom}(\varphi ^{M_\kappa })$
, since
![]() $r^*\geq q^*\geq p^*(M_\kappa )$
. Let
$r^*\geq q^*\geq p^*(M_\kappa )$
. Let
![]() $r\in \mathbb {P}^*$
so that
$r\in \mathbb {P}^*$
so that
![]() $\varphi ^{M_\kappa }(r^*)=j(r)$
.
$\varphi ^{M_\kappa }(r^*)=j(r)$
.
Now,
![]() $r^*\geq _{j(\mathbb {P}^*)}q^{**}$
are both in
$r^*\geq _{j(\mathbb {P}^*)}q^{**}$
are both in
![]() $\operatorname {dom}(\varphi ^{M_\kappa })$
. Since
$\operatorname {dom}(\varphi ^{M_\kappa })$
. Since
![]() $\varphi ^{M_\kappa }$
is order-preserving,
$\varphi ^{M_\kappa }$
is order-preserving,
![]() $j(r)=\varphi ^{M_\kappa }(r^*)\geq \varphi ^{M_\kappa }(q^{**})\geq j(u)$
. Then
$j(r)=\varphi ^{M_\kappa }(r^*)\geq \varphi ^{M_\kappa }(q^{**})\geq j(u)$
. Then
![]() $r\geq u$
. As a result,
$r\geq u$
. As a result,
![]() $r\Vdash ^V\dot {h}_\gamma =\dot {f}_\gamma \in \dot {A}(1)$
. By definition of
$r\Vdash ^V\dot {h}_\gamma =\dot {f}_\gamma \in \dot {A}(1)$
. By definition of
![]() $\dot {A}(1)$
, we may find some
$\dot {A}(1)$
, we may find some
![]() $\mathbb {P}^*$
-extension
$\mathbb {P}^*$
-extension
![]() $r'$
of r so that
$r'$
of r so that
![]() $(r',\dot {h}_\gamma )$
extends some element
$(r',\dot {h}_\gamma )$
extends some element
![]() $(r^{\prime }_0,\dot {f})$
of A. Then
$(r^{\prime }_0,\dot {f})$
of A. Then
![]() $j(r^{\prime }_0,\dot {f})\in A^*$
, as
$j(r^{\prime }_0,\dot {f})\in A^*$
, as
![]() $A=j^{-1}[A^*]$
. Since
$A=j^{-1}[A^*]$
. Since
![]() $r'$
extends r in
$r'$
extends r in
![]() $\mathbb {P}^*$
, we get that
$\mathbb {P}^*$
, we get that
![]() $j(r')\geq _{j(\mathbb {P}^*)}j(r)=\varphi ^{M_\kappa }(r^*)$
. So
$j(r')\geq _{j(\mathbb {P}^*)}j(r)=\varphi ^{M_\kappa }(r^*)$
. So
![]() $j(r')$
and
$j(r')$
and
![]() $r^*$
are compatible in
$r^*$
are compatible in
![]() $j(\mathbb {P}^*)$
. Let
$j(\mathbb {P}^*)$
. Let
![]() $r^{**}$
be a condition extending both of them. Then
$r^{**}$
be a condition extending both of them. Then
![]() $(r^{**},\dot {g}^*)$
extends
$(r^{**},\dot {g}^*)$
extends
![]() $j(r^{\prime }_0,\dot {f})$
. Indeed,
$j(r^{\prime }_0,\dot {f})$
. Indeed,
![]() $r^{**}$
extends
$r^{**}$
extends
![]() $j(r')$
which extends
$j(r')$
which extends
![]() $j(r^{\prime }_0)$
. Furthermore,
$j(r^{\prime }_0)$
. Furthermore,
![]() $r^{**}$
extends
$r^{**}$
extends
![]() $r^*$
which forces that
$r^*$
which forces that
![]() $\dot {g}^*\geq j(\dot {h}_\gamma )$
, and
$\dot {g}^*\geq j(\dot {h}_\gamma )$
, and
![]() $r^*$
extends
$r^*$
extends
![]() $j(r')$
which forces that
$j(r')$
which forces that
![]() $j(\dot {h}_\gamma )\geq j(\dot {f})$
. Thus,
$j(\dot {h}_\gamma )\geq j(\dot {f})$
. Thus,
![]() $(r^{**},\dot {g}^*)$
extends
$(r^{**},\dot {g}^*)$
extends
![]() $j(r^{\prime }_0,\dot {f})$
, and therefore
$j(r^{\prime }_0,\dot {f})$
, and therefore
However,
![]() $(r^{**},\dot {g}^*)$
also extends the starting condition
$(r^{**},\dot {g}^*)$
also extends the starting condition
![]() $(q^*,\dot {g})$
. This finishes the proof that
$(q^*,\dot {g})$
. This finishes the proof that
![]() $\kappa $
is not a member of
$\kappa $
is not a member of
![]() $j(B_1)$
, which contradicts our initial case assumption otherwise.
$j(B_1)$
, which contradicts our initial case assumption otherwise.
Case 2:
![]() $i=2$
. In this case, we are assuming that
$i=2$
. In this case, we are assuming that
![]() $\kappa \in j(B_2)$
, and we will derive a contradiction. Let
$\kappa \in j(B_2)$
, and we will derive a contradiction. Let
![]() $\langle p^*(M_\kappa ),\varphi ^{M_\kappa }\rangle $
be a residue pair for
$\langle p^*(M_\kappa ),\varphi ^{M_\kappa }\rangle $
be a residue pair for
![]() $(M_\kappa ,j(\mathbb {P}^*))$
so that
$(M_\kappa ,j(\mathbb {P}^*))$
so that
![]() $(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\zeta )})$
does not force the desired equality. We will show, however, that this residue pair does in fact force the desired equality.
$(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\zeta )})$
does not force the desired equality. We will show, however, that this residue pair does in fact force the desired equality.
Toward this end, let
![]() $G^*$
be V-generic for
$G^*$
be V-generic for
![]() $j(\mathbb {R}_\zeta )$
containing
$j(\mathbb {R}_\zeta )$
containing
![]() $(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\zeta )})$
, and let
$(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\zeta )})$
, and let
![]() $\bar {G}^*:=G^*\cap M_\kappa $
which, by item (1), is a V-generic filter over
$\bar {G}^*:=G^*\cap M_\kappa $
which, by item (1), is a V-generic filter over
![]() $j(\mathbb {R}_\zeta )\cap M_\kappa =j[\mathbb {R}_\zeta ]$
. Let
$j(\mathbb {R}_\zeta )\cap M_\kappa =j[\mathbb {R}_\zeta ]$
. Let
![]() $G:=j^{-1}[\bar {G}^*]$
, which is V-generic over
$G:=j^{-1}[\bar {G}^*]$
, which is V-generic over
![]() $\mathbb {R}_\zeta $
. Let
$\mathbb {R}_\zeta $
. Let
![]() $j(T_\zeta )$
denote
$j(T_\zeta )$
denote
![]() $j(\dot {T}_\zeta )[G^*]$
, let
$j(\dot {T}_\zeta )[G^*]$
, let
![]() $T_\zeta :=\dot {T}_\zeta [G]$
, and let
$T_\zeta :=\dot {T}_\zeta [G]$
, and let
![]() $T^{\prime }_\zeta :=(j(\dot {T}_\zeta )\cap M_\kappa )[\bar {G}^*]=j[\dot {T}_\zeta ][\bar {G}^*]$
.
$T^{\prime }_\zeta :=(j(\dot {T}_\zeta )\cap M_\kappa )[\bar {G}^*]=j[\dot {T}_\zeta ][\bar {G}^*]$
.
Since
![]() $\dot {T}_\zeta $
is a nice
$\dot {T}_\zeta $
is a nice
![]() $\mathbb {R}_\zeta $
-name for a tree order on
$\mathbb {R}_\zeta $
-name for a tree order on
![]() $\kappa $
, for each
$\kappa $
, for each
![]() $\tau ,\theta \in \kappa \times \omega _1$
, there exists an antichain
$\tau ,\theta \in \kappa \times \omega _1$
, there exists an antichain
![]() $B_{\theta ,\tau }$
of
$B_{\theta ,\tau }$
of
![]() $\mathbb {R}_\zeta $
so that, letting
$\mathbb {R}_\zeta $
so that, letting
![]() $\operatorname {op}(\theta ,\tau )$
denote the canonical name for
$\operatorname {op}(\theta ,\tau )$
denote the canonical name for
![]() $\langle \theta ,\tau \rangle $
,
$\langle \theta ,\tau \rangle $
,
It is straightforward to see from this that
![]() $T_\zeta =T^{\prime }_\zeta $
. So we will show that
$T_\zeta =T^{\prime }_\zeta $
. So we will show that
![]() $T_\zeta $
equals the restriction of
$T_\zeta $
equals the restriction of
![]() $j(T_\zeta )$
to
$j(T_\zeta )$
to
![]() $\kappa \times \omega _1$
. However, we know that
$\kappa \times \omega _1$
. However, we know that
![]() $j:M^*\longrightarrow N$
lifts to
$j:M^*\longrightarrow N$
lifts to
![]() $j:M^*[G]\longrightarrow N[G^*]$
, since
$j:M^*[G]\longrightarrow N[G^*]$
, since
![]() $j[G]=\bar {G}^*\subseteq G^*$
and since each of the filters is generic over the appropriate models. From this, it follows that
$j[G]=\bar {G}^*\subseteq G^*$
and since each of the filters is generic over the appropriate models. From this, it follows that
![]() $T_\zeta =j(T_\zeta )\cap (\kappa \times \omega _1)$
. Therefore, the equality in (2) is in fact satisfied, which contradicts the assumption that
$T_\zeta =j(T_\zeta )\cap (\kappa \times \omega _1)$
. Therefore, the equality in (2) is in fact satisfied, which contradicts the assumption that
![]() $\kappa \in j(B_2)$
.
$\kappa \in j(B_2)$
.
Case 3:
![]() $i=3$
. Let
$i=3$
. Let
![]() $j(q)\in j[\mathbb {P}^*]=j(\mathbb {P}^*)\cap M_\kappa $
be a condition forcing that
$j(q)\in j[\mathbb {P}^*]=j(\mathbb {P}^*)\cap M_\kappa $
be a condition forcing that
![]() $\dot {A}$
is a name for a
$\dot {A}$
is a name for a
![]() $\kappa $
-sized antichain in
$\kappa $
-sized antichain in
![]() $j(\dot {\mathbb {S}}_\zeta )\cap M_\kappa $
. Since B satisfies Definition 2.8, and since
$j(\dot {\mathbb {S}}_\zeta )\cap M_\kappa $
. Since B satisfies Definition 2.8, and since
![]() $B_1\subseteq B$
is in U, we may fix a residue pair
$B_1\subseteq B$
is in U, we may fix a residue pair
![]() $(p^*(M_\kappa ),\varphi ^{M_\kappa })$
for
$(p^*(M_\kappa ),\varphi ^{M_\kappa })$
for
![]() $(M_\kappa ,j(\mathbb {P}^*))$
. Let
$(M_\kappa ,j(\mathbb {P}^*))$
. Let
![]() $q^*\geq q,p^*(M_\kappa )$
be a condition, and let
$q^*\geq q,p^*(M_\kappa )$
be a condition, and let
![]() $G^*$
be a V-generic filter over
$G^*$
be a V-generic filter over
![]() $j(\mathbb {P}^*)$
containing
$j(\mathbb {P}^*)$
containing
![]() $q^*$
. Then
$q^*$
. Then
![]() $\bar {G}^*$
is a V-generic filter over
$\bar {G}^*$
is a V-generic filter over
![]() $j(\mathbb {P}^*)\cap M_\kappa =j[\mathbb {P}^*]$
. We recall that
$j(\mathbb {P}^*)\cap M_\kappa =j[\mathbb {P}^*]$
. We recall that
![]() $j^{-1}:M_\kappa \longrightarrow \bigcup _{\alpha \in B_1}M_\alpha $
is the transitive collapse, and that
$j^{-1}:M_\kappa \longrightarrow \bigcup _{\alpha \in B_1}M_\alpha $
is the transitive collapse, and that
![]() $j^{-1}$
lifts in the standard way from
$j^{-1}$
lifts in the standard way from
![]() $M_\kappa [G^*]$
to
$M_\kappa [G^*]$
to
![]() $(\bigcup _{\alpha \in B_1}M_\alpha )[G]$
. Now, let
$(\bigcup _{\alpha \in B_1}M_\alpha )[G]$
. Now, let
![]() $A:=\dot {A}[\bar {G}^*]$
so that A is an antichain in
$A:=\dot {A}[\bar {G}^*]$
so that A is an antichain in
![]() $(j(\dot {\mathbb {S}}_\zeta )\cap M_\kappa )[\bar {G}^*]= j[\dot {\mathbb {S}}_\zeta ][\bar {G}^*]=j(\dot {\mathbb {S}}_\zeta [G^*])\cap M_\kappa [G^*]$
. Furthermore, A is a member of
$(j(\dot {\mathbb {S}}_\zeta )\cap M_\kappa )[\bar {G}^*]= j[\dot {\mathbb {S}}_\zeta ][\bar {G}^*]=j(\dot {\mathbb {S}}_\zeta [G^*])\cap M_\kappa [G^*]$
. Furthermore, A is a member of
![]() $V[\bar {G}^*]$
and has size
$V[\bar {G}^*]$
and has size
![]() $\kappa $
there. Applying the elementarity of
$\kappa $
there. Applying the elementarity of
![]() $j^{-1}$
, we have that
$j^{-1}$
, we have that
![]() $j^{-1}[A]=:\bar {A}$
is an antichain in
$j^{-1}[A]=:\bar {A}$
is an antichain in
![]() $\dot {\mathbb {S}}_\zeta [G]$
, where
$\dot {\mathbb {S}}_\zeta [G]$
, where
![]() $G:=j^{-1}[\bar {G}^*]$
is V-generic over
$G:=j^{-1}[\bar {G}^*]$
is V-generic over
![]() $\mathbb {P}^*$
. Finally,
$\mathbb {P}^*$
. Finally,
![]() $\bar {A}\in V[G]$
since
$\bar {A}\in V[G]$
since
![]() $j^{-1}[\dot {A}]$
is a
$j^{-1}[\dot {A}]$
is a
![]() $\mathbb {P}^*$
-name in V and
$\mathbb {P}^*$
-name in V and
![]() $\bar {A}=j^{-1}[\dot {A}][G]$
. Since
$\bar {A}=j^{-1}[\dot {A}][G]$
. Since
![]() $\bar {A}$
has size
$\bar {A}$
has size
![]() $\kappa $
in
$\kappa $
in
![]() $V[G]=V[\bar {G}^*]$
, this contradicts the assumption that
$V[G]=V[\bar {G}^*]$
, this contradicts the assumption that
![]() $\mathbb {P}^*\Vdash \dot {\mathbb {S}}_\zeta $
is
$\mathbb {P}^*\Vdash \dot {\mathbb {S}}_\zeta $
is
![]() $\kappa $
-c.c.
$\kappa $
-c.c.
For the “furthermore” part of (3), suppose now that
![]() $\dot {b}'$
is a
$\dot {b}'$
is a
![]() $j(\mathbb {R}_\zeta )\cap M_\kappa =j[\mathbb {R}_\zeta ]$
-name which
$j(\mathbb {R}_\zeta )\cap M_\kappa =j[\mathbb {R}_\zeta ]$
-name which
![]() $j(q)$
forces is a branch through
$j(q)$
forces is a branch through
![]() $j(\dot {T}_\zeta )\cap M_\kappa $
. Fix
$j(\dot {T}_\zeta )\cap M_\kappa $
. Fix
![]() $q^*$
and
$q^*$
and
![]() $G^*$
as in the previous paragraph. Then, by (2), we see that
$G^*$
as in the previous paragraph. Then, by (2), we see that
![]() $j(\dot {T}_\zeta )[G^*]\cap (\kappa \times \omega _1)=\dot {T}_\zeta [G]$
. Moreover,
$j(\dot {T}_\zeta )[G^*]\cap (\kappa \times \omega _1)=\dot {T}_\zeta [G]$
. Moreover,
![]() $j(\dot {T}_\zeta )[G^*]\cap (\kappa \times \omega _1)=j(\dot {T}_\zeta )[G^*]\cap M_\kappa [G^*]=(j(\dot {T}_\zeta )\cap M_\kappa )[\bar {G}^*]$
. Thus,
$j(\dot {T}_\zeta )[G^*]\cap (\kappa \times \omega _1)=j(\dot {T}_\zeta )[G^*]\cap M_\kappa [G^*]=(j(\dot {T}_\zeta )\cap M_\kappa )[\bar {G}^*]$
. Thus,
![]() $\dot {b}'[\bar {G}^*]$
is a branch through
$\dot {b}'[\bar {G}^*]$
is a branch through
![]() $T_\zeta :=\dot {T}_\zeta [G]$
. However,
$T_\zeta :=\dot {T}_\zeta [G]$
. However,
![]() $\dot {b}'[\bar {G}^*]$
is a member of
$\dot {b}'[\bar {G}^*]$
is a member of
![]() $V[\bar {G}^*]$
and
$V[\bar {G}^*]$
and
![]() $V[\bar {G}^*]=V[G]$
. Thus,
$V[\bar {G}^*]=V[G]$
. Thus,
![]() $T_\zeta $
is not Aronszajn in
$T_\zeta $
is not Aronszajn in
![]() $V[G]$
, a contradiction.
$V[G]$
, a contradiction.
Thus, we see that
![]() $\kappa $
cannot be a member of
$\kappa $
cannot be a member of
![]() $j(B_3)$
, completing Case 3 and thereby the proof.
$j(B_3)$
, completing Case 3 and thereby the proof.
In both the previous result and Definition 2.8, there was the apparent necessity of refining the domain of a suitable sequence so that various desired behavior obtains on each level of the refined sequence. The next item amalgamates this into one definition which we use frequently throughout.
Definition 3.4 Let
![]() $\vec {M}$
be an
$\vec {M}$
be an
![]() $\mathbb {R}_\rho $
-suitable sequence. We say that
$\mathbb {R}_\rho $
-suitable sequence. We say that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
if there is a residue system
$\rho $
if there is a residue system
![]() $\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in \operatorname {dom}(\vec {M})\rangle $
satisfying items (1) and (2) of Definition 2.8 (with respect to
$\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in \operatorname {dom}(\vec {M})\rangle $
satisfying items (1) and (2) of Definition 2.8 (with respect to
![]() $\mathbb {P}^*$
) as well as items (1)–(3) of Proposition 3.2 for all
$\mathbb {P}^*$
) as well as items (1)–(3) of Proposition 3.2 for all
![]() $\alpha \in \operatorname {dom}(\vec {M})$
(with respect to
$\alpha \in \operatorname {dom}(\vec {M})$
(with respect to
![]() $\mathbb {R}_\rho $
).
$\mathbb {R}_\rho $
).
Definition 3.5 Suppose that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
,
$\rho $
,
![]() $\xi \leq \rho $
, and
$\xi \leq \rho $
, and
![]() $\alpha \in \operatorname {dom}(\vec {M})$
so that
$\alpha \in \operatorname {dom}(\vec {M})$
so that
![]() $\xi \in M_\alpha $
. Fix a residue pair
$\xi \in M_\alpha $
. Fix a residue pair
![]() $\langle p^*(M_\alpha ), \varphi ^{M_\alpha }\rangle $
for
$\langle p^*(M_\alpha ), \varphi ^{M_\alpha }\rangle $
for
![]() $(M_\alpha ,\mathbb {P}^*)$
.
$(M_\alpha ,\mathbb {P}^*)$
.
-
(1) For a (determined) condition
 $(p,f)$
, we define
$(p,f)$
, we define
 $f\upharpoonright M_\alpha $
to be the function
$f\upharpoonright M_\alpha $
to be the function
 $\bar {f}$
with domain
$\bar {f}$
with domain
 $\operatorname {dom}(f)\cap M_\alpha $
so that for each
$\operatorname {dom}(f)\cap M_\alpha $
so that for each
 $\langle \zeta ,\nu \rangle \in \operatorname {dom}(f)\cap M_\alpha $
,
$\langle \zeta ,\nu \rangle \in \operatorname {dom}(f)\cap M_\alpha $
,  $$ \begin{align*}\bar{f}(\zeta,\nu)=f(\zeta,\nu)\cap M_\alpha. \end{align*} $$
$$ \begin{align*}\bar{f}(\zeta,\nu)=f(\zeta,\nu)\cap M_\alpha. \end{align*} $$
-
(2) We define
 $D(\varphi ^{M_\alpha },\xi )$
to be the set of conditions
$D(\varphi ^{M_\alpha },\xi )$
to be the set of conditions
 $( p,f)\in \mathbb {R}_\xi $
so that
$( p,f)\in \mathbb {R}_\xi $
so that
 $p\in \operatorname {dom}(\varphi ^{M_\alpha })$
and
$p\in \operatorname {dom}(\varphi ^{M_\alpha })$
and
 $(\varphi ^{M_\alpha }(p),f\upharpoonright M_\alpha )$
is a condition in
$(\varphi ^{M_\alpha }(p),f\upharpoonright M_\alpha )$
is a condition in
 $\mathbb {R}_\xi $
(and hence in
$\mathbb {R}_\xi $
(and hence in
 $\mathbb {R}_\xi \cap M_\alpha $
).
$\mathbb {R}_\xi \cap M_\alpha $
). -
(3) If
 $( p,f)\in D(\varphi ^{M_\alpha },\xi )$
, we make a slight abuse of notation and define
$( p,f)\in D(\varphi ^{M_\alpha },\xi )$
, we make a slight abuse of notation and define
 $( p,f )\upharpoonright M_\alpha $
to be the pair
$( p,f )\upharpoonright M_\alpha $
to be the pair
 $(\varphi ^{M_\alpha }(p),f\upharpoonright M_\alpha )$
, when
$(\varphi ^{M_\alpha }(p),f\upharpoonright M_\alpha )$
, when
 $\varphi ^{M_\alpha }$
is clear from context.
$\varphi ^{M_\alpha }$
is clear from context.
We observe that, in general, for
![]() $(p,f) \in D(\varphi ^{M_\alpha },\xi )$
, although
$(p,f) \in D(\varphi ^{M_\alpha },\xi )$
, although
![]() $(p,f)\upharpoonright M_\alpha \in \mathbb {R}_\xi \cap M_\alpha $
is a condition, it need not be a residue of
$(p,f)\upharpoonright M_\alpha \in \mathbb {R}_\xi \cap M_\alpha $
is a condition, it need not be a residue of
![]() $(p,f)$
to
$(p,f)$
to
![]() $M_\alpha $
in the sense that it is possible for some
$M_\alpha $
in the sense that it is possible for some
![]() $(p',f') \in \mathbb {R}_\xi \cap M_\alpha $
which extends
$(p',f') \in \mathbb {R}_\xi \cap M_\alpha $
which extends
![]() $(p,f)\upharpoonright M_\alpha $
not to be compatible with
$(p,f)\upharpoonright M_\alpha $
not to be compatible with
![]() $(p,f)$
. However,
$(p,f)$
. However,
![]() $(p,f)\upharpoonright M_\alpha $
must have some extension
$(p,f)\upharpoonright M_\alpha $
must have some extension
![]() $(\bar {p},\bar {f}) \in \mathbb {R}_\xi \cap M_\alpha $
which is a residue of
$(\bar {p},\bar {f}) \in \mathbb {R}_\xi \cap M_\alpha $
which is a residue of
![]() $(p,f)$
. This is because if
$(p,f)$
. This is because if
![]() $G \subseteq \mathbb {R}_\xi $
is V-generic and contains
$G \subseteq \mathbb {R}_\xi $
is V-generic and contains
![]() $(p,f)$
, then by Proposition 3.2 and the definition of pre-splitting configuration,
$(p,f)$
, then by Proposition 3.2 and the definition of pre-splitting configuration,
![]() $\bar {G}:=G\cap M_\alpha $
is V-generic over
$\bar {G}:=G\cap M_\alpha $
is V-generic over
![]() $\mathbb {R}_\xi \cap M_\alpha $
and
$\mathbb {R}_\xi \cap M_\alpha $
and
![]() $(p,f)\upharpoonright M_\alpha \in \bar {G}$
. Since
$(p,f)\upharpoonright M_\alpha \in \bar {G}$
. Since
![]() $(p,f)\in G$
is compatible with every condition in
$(p,f)\in G$
is compatible with every condition in
![]() $\bar {G}$
, there must be some
$\bar {G}$
, there must be some
![]() $(\bar {p},\bar {f}) \in \bar {G}$
which extends
$(\bar {p},\bar {f}) \in \bar {G}$
which extends
![]() $(p,f)\upharpoonright M_\alpha $
and is a residue of
$(p,f)\upharpoonright M_\alpha $
and is a residue of
![]() $(p,f)$
, by Lemma 2.3.
$(p,f)$
, by Lemma 2.3.
Lemma 3.3 Suppose that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
. Then, for each
$\rho $
. Then, for each
![]() $\alpha \in \operatorname {dom}(\vec {M})$
, each residue pair
$\alpha \in \operatorname {dom}(\vec {M})$
, each residue pair
![]() $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
![]() $(M_\alpha ,\mathbb {P}^*)$
, and each
$(M_\alpha ,\mathbb {P}^*)$
, and each
![]() $\xi \leq \rho $
with
$\xi \leq \rho $
with
![]() $\xi \in M_\alpha $
,
$\xi \in M_\alpha $
,
![]() $D(\varphi ^{M_\alpha },\xi )$
is dense and
$D(\varphi ^{M_\alpha },\xi )$
is dense and
![]() $=^*$
-countably closed in
$=^*$
-countably closed in
![]() $(\mathbb {P}^*/p^*(M_\alpha ))\ast \dot {\mathbb {S}}_\xi $
.
$(\mathbb {P}^*/p^*(M_\alpha ))\ast \dot {\mathbb {S}}_\xi $
.
Proof We will first prove the result for
![]() $\xi <\rho $
and then use this to prove the result at
$\xi <\rho $
and then use this to prove the result at
![]() $\rho $
. Note that the
$\rho $
. Note that the
![]() $=^*$
-countable closure of
$=^*$
-countable closure of
![]() $D(\varphi ^{M_\alpha },\xi )$
, in either case for
$D(\varphi ^{M_\alpha },\xi )$
, in either case for
![]() $\xi $
, follows from the continuity of
$\xi $
, follows from the continuity of
![]() $\varphi ^{M_\alpha }$
and the
$\varphi ^{M_\alpha }$
and the
![]() $=^*$
-countable closure of the posets. We therefore concentrate on showing density.
$=^*$
-countable closure of the posets. We therefore concentrate on showing density.
Let
![]() $(p_0,f_0)\in \mathbb {R}_\xi $
be given with
$(p_0,f_0)\in \mathbb {R}_\xi $
be given with
![]() $p_0\geq p^*(M_\alpha )$
. By the observations following Definition 3.5, we may build increasing sequences
$p_0\geq p^*(M_\alpha )$
. By the observations following Definition 3.5, we may build increasing sequences
![]() $\langle (p_n,f_n):n\in \omega \rangle $
and
$\langle (p_n,f_n):n\in \omega \rangle $
and
![]() $\langle (\bar {p}_n,\bar {f}_n):n\in \omega \rangle $
so that:
$\langle (\bar {p}_n,\bar {f}_n):n\in \omega \rangle $
so that:
-
(i)
 $(\bar {p}_n,\bar {f}_n)$
is a residue of
$(\bar {p}_n,\bar {f}_n)$
is a residue of
 $(p_n,f_n)$
to
$(p_n,f_n)$
to
 $M_\alpha $
with
$M_\alpha $
with
 $\bar {p}_n$
extending
$\bar {p}_n$
extending
 $\varphi ^{M_\alpha }(p_n)$
and with
$\varphi ^{M_\alpha }(p_n)$
and with
 $\bar {f}_n$
extending the function
$\bar {f}_n$
extending the function
 $f_n\upharpoonright M_\alpha $
in the sense of Definition 3.2 (note that
$f_n\upharpoonright M_\alpha $
in the sense of Definition 3.2 (note that
 $f_n\upharpoonright M_\alpha $
need not be forced by
$f_n\upharpoonright M_\alpha $
need not be forced by
 $\varphi ^{M_\alpha }(p_n)$
to be a condition);
$\varphi ^{M_\alpha }(p_n)$
to be a condition); -
(ii)
 $(p_{n+1},f_{n+1})$
extends both
$(p_{n+1},f_{n+1})$
extends both
 $(p_n,f_n)$
and
$(p_n,f_n)$
and
 $(\bar {p}_n,\bar {f}_n)$
; and
$(\bar {p}_n,\bar {f}_n)$
; and -
(iii)
 $p_{n+1}\in \operatorname {dom}(\varphi ^{M_\alpha })$
and
$p_{n+1}\in \operatorname {dom}(\varphi ^{M_\alpha })$
and
 $\varphi ^{M_\alpha }(p_{n+1})\geq \bar {p}_n$
.
$\varphi ^{M_\alpha }(p_{n+1})\geq \bar {p}_n$
.
Now, let
![]() $(p^*,f^*)$
be a sup of
$(p^*,f^*)$
be a sup of
![]() $\langle (p_n,f_n):n\in \omega \rangle $
. Note that
$\langle (p_n,f_n):n\in \omega \rangle $
. Note that
![]() $p^*\in \operatorname {dom}(\varphi ^{M_\alpha })$
since
$p^*\in \operatorname {dom}(\varphi ^{M_\alpha })$
since
![]() $p_n\in \operatorname {dom}(\varphi ^{M_\alpha })$
for each n and also that
$p_n\in \operatorname {dom}(\varphi ^{M_\alpha })$
for each n and also that
![]() $\varphi ^{M_\alpha }(p^*)$
is a sup of
$\varphi ^{M_\alpha }(p^*)$
is a sup of
![]() $\langle \varphi ^{M_\alpha }(p_n):n\in \omega \rangle $
. We claim that
$\langle \varphi ^{M_\alpha }(p_n):n\in \omega \rangle $
. We claim that
![]() $(\varphi ^{M_\alpha }(p^*),f^*\upharpoonright M_\alpha )$
is a condition. Now,
$(\varphi ^{M_\alpha }(p^*),f^*\upharpoonright M_\alpha )$
is a condition. Now,
![]() $\varphi ^{M_\alpha }(p^*)\geq \varphi ^{M_\alpha }(p_{n+1})\geq \bar {p}_n$
for each n, so
$\varphi ^{M_\alpha }(p^*)\geq \varphi ^{M_\alpha }(p_{n+1})\geq \bar {p}_n$
for each n, so
![]() $\varphi ^{M_\alpha }(p^*)$
forces that
$\varphi ^{M_\alpha }(p^*)$
forces that
![]() $\langle \bar {f}_n:n\in \omega \rangle $
is an increasing sequence of conditions in
$\langle \bar {f}_n:n\in \omega \rangle $
is an increasing sequence of conditions in
![]() $\dot {\mathbb {S}}_\xi $
, and therefore forces that
$\dot {\mathbb {S}}_\xi $
, and therefore forces that
![]() $\bigcup _n\bar {f}_n$
is a condition too. However,
$\bigcup _n\bar {f}_n$
is a condition too. However,
![]() $\bar {f}_{n+1}$
extends (in the sense of Definition 3.2)
$\bar {f}_{n+1}$
extends (in the sense of Definition 3.2)
![]() $f_{n+1}\upharpoonright M_\alpha $
which extends
$f_{n+1}\upharpoonright M_\alpha $
which extends
![]() $\bar {f}_n$
for all n. Therefore,
$\bar {f}_n$
for all n. Therefore,
![]() $\bigcup _n\bar {f}_n=\bigcup _n(f_n\upharpoonright M_\alpha )=(\bigcup _nf_n)\upharpoonright M_\alpha =f^*\upharpoonright M_\alpha $
, which finishes the claim.
$\bigcup _n\bar {f}_n=\bigcup _n(f_n\upharpoonright M_\alpha )=(\bigcup _nf_n)\upharpoonright M_\alpha =f^*\upharpoonright M_\alpha $
, which finishes the claim.
Now, we show that the lemma holds for
![]() $\xi =\rho $
. We deal with
$\xi =\rho $
. We deal with
![]() $\rho $
limit first. If
$\rho $
limit first. If
![]() $\operatorname {cf}(\rho )\,{>}\,\omega $
, then the result holds since any
$\operatorname {cf}(\rho )\,{>}\,\omega $
, then the result holds since any
![]() $(p,f)\in \mathbb {R}_\rho $
is in
$(p,f)\in \mathbb {R}_\rho $
is in
![]() $\mathbb {R}_\xi $
for some
$\mathbb {R}_\xi $
for some
![]() $\xi <\rho $
. On the other hand, if
$\xi <\rho $
. On the other hand, if
![]() $\operatorname {cf}(\rho )=\omega $
, then let
$\operatorname {cf}(\rho )=\omega $
, then let
![]() $\langle \xi _n:n\in \omega \rangle $
be an increasing sequence of ordinals in
$\langle \xi _n:n\in \omega \rangle $
be an increasing sequence of ordinals in
![]() $M_\alpha $
which is cofinal in
$M_\alpha $
which is cofinal in
![]() $\rho $
. By applying the lemma below
$\rho $
. By applying the lemma below
![]() $\rho $
, we define an increasing sequence of extensions
$\rho $
, we define an increasing sequence of extensions
![]() $\langle (p_n,f_n):n\in \omega \rangle $
of
$\langle (p_n,f_n):n\in \omega \rangle $
of
![]() $(p,f)$
so that
$(p,f)$
so that
![]() $f_n\upharpoonright [\xi _n,\rho )=f\upharpoonright [\xi _n,\rho )$
and so that
$f_n\upharpoonright [\xi _n,\rho )=f\upharpoonright [\xi _n,\rho )$
and so that
![]() $(p_n,f_n\upharpoonright \xi _n)\in D(\varphi ^{M_\alpha },\xi _n)$
. Now, let
$(p_n,f_n\upharpoonright \xi _n)\in D(\varphi ^{M_\alpha },\xi _n)$
. Now, let
![]() $p^*$
be a sup of
$p^*$
be a sup of
![]() $\langle p_n:n\in \omega \rangle $
and
$\langle p_n:n\in \omega \rangle $
and
![]() $f^*:=\bigcup _nf_n$
. Then
$f^*:=\bigcup _nf_n$
. Then
![]() $(p^*,f^*)$
extends
$(p^*,f^*)$
extends
![]() $(p,f)$
and is a member of
$(p,f)$
and is a member of
![]() $D(\varphi ^{M_\alpha },\rho )$
.
$D(\varphi ^{M_\alpha },\rho )$
.
Finally, assume that
![]() $\rho =\rho _0+1$
is a successor, and let
$\rho =\rho _0+1$
is a successor, and let
![]() $(p,h)\in \mathbb {R}_\rho $
be given. By the remarks after Definition 3.5, we may find a residue
$(p,h)\in \mathbb {R}_\rho $
be given. By the remarks after Definition 3.5, we may find a residue
![]() $(\bar {p},\bar {h}_0)$
of
$(\bar {p},\bar {h}_0)$
of
![]() $(p,h\upharpoonright \rho _0)$
to
$(p,h\upharpoonright \rho _0)$
to
![]() $M_\alpha $
with respect to the poset
$M_\alpha $
with respect to the poset
![]() $\mathbb {R}_{\rho _0}$
. Recalling Notation 3.1, we use
$\mathbb {R}_{\rho _0}$
. Recalling Notation 3.1, we use
![]() $h(\rho _0)\cap M_\alpha $
in what follows as an abuse of notation for
$h(\rho _0)\cap M_\alpha $
in what follows as an abuse of notation for
![]() $\langle h(\rho _0)(\nu )\cap M_\alpha :\nu \in \operatorname {dom}(h(\rho _0))\rangle $
. By the elementarity of
$\langle h(\rho _0)(\nu )\cap M_\alpha :\nu \in \operatorname {dom}(h(\rho _0))\rangle $
. By the elementarity of
![]() $M_\alpha $
and the fact that
$M_\alpha $
and the fact that
![]() $h(\rho _0)\cap M_\alpha $
is a member of
$h(\rho _0)\cap M_\alpha $
is a member of
![]() $M_\alpha $
, we may find an extension of
$M_\alpha $
, we may find an extension of
![]() $(\bar {p},\bar {h}_0)$
, say
$(\bar {p},\bar {h}_0)$
, say
![]() $(\bar {p}',\bar {h}^{\prime }_0)$
, which either forces that
$(\bar {p}',\bar {h}^{\prime }_0)$
, which either forces that
![]() $h(\rho _0)\cap M_\alpha \in \dot {\mathbb {S}}(\rho _0)$
or forces that
$h(\rho _0)\cap M_\alpha \in \dot {\mathbb {S}}(\rho _0)$
or forces that
![]() $h(\rho _0)\cap M_\alpha \notin \dot {\mathbb {S}}(\rho _0)$
. Since
$h(\rho _0)\cap M_\alpha \notin \dot {\mathbb {S}}(\rho _0)$
. Since
![]() $(\bar {p}',\bar {h}^{\prime }_0)$
extends
$(\bar {p}',\bar {h}^{\prime }_0)$
extends
![]() $(\bar {p},\bar {h}_0)$
, it is compatible with
$(\bar {p},\bar {h}_0)$
, it is compatible with
![]() $(p,h\upharpoonright \rho _0)$
, and hence it must force that
$(p,h\upharpoonright \rho _0)$
, and hence it must force that
![]() $h(\rho _0)\cap M_\alpha \in \dot {\mathbb {S}}(\rho _0)$
. Finally, since
$h(\rho _0)\cap M_\alpha \in \dot {\mathbb {S}}(\rho _0)$
. Finally, since
![]() $D(\varphi ^{M_\alpha },\rho _0)$
is dense and
$D(\varphi ^{M_\alpha },\rho _0)$
is dense and
![]() $\rho _0\in M_\alpha $
, we may find an extension
$\rho _0\in M_\alpha $
, we may find an extension
![]() $(q,g_0)$
of
$(q,g_0)$
of
![]() $(\bar {p}',\bar {h}^{\prime }_0)$
and
$(\bar {p}',\bar {h}^{\prime }_0)$
and
![]() $(p,h\upharpoonright \rho _0)$
which is in
$(p,h\upharpoonright \rho _0)$
which is in
![]() $D(\varphi ^{M_\alpha },\rho _0)$
and which satisfies that
$D(\varphi ^{M_\alpha },\rho _0)$
and which satisfies that
![]() $\varphi ^{M_\alpha }(q)\geq \bar {p}'$
. Then
$\varphi ^{M_\alpha }(q)\geq \bar {p}'$
. Then
![]() $(q,g_0)\upharpoonright M_\alpha $
is a condition which forces that
$(q,g_0)\upharpoonright M_\alpha $
is a condition which forces that
![]() $h(\rho _0)\cap M_\alpha $
is a condition in
$h(\rho _0)\cap M_\alpha $
is a condition in
![]() $\dot {\mathbb {S}}(\rho _0)$
. Thus,
$\dot {\mathbb {S}}(\rho _0)$
. Thus,
![]() $(\varphi ^{M_\alpha }(q),(g_0\upharpoonright M_\alpha )^\frown \langle h(\rho _0)\cap M_\alpha \rangle )$
is a condition and equals
$(\varphi ^{M_\alpha }(q),(g_0\upharpoonright M_\alpha )^\frown \langle h(\rho _0)\cap M_\alpha \rangle )$
is a condition and equals
![]() $(q,g_0^\frown \langle h(\rho _0)\rangle )\upharpoonright M_\alpha $
.▪
$(q,g_0^\frown \langle h(\rho _0)\rangle )\upharpoonright M_\alpha $
.▪
Notation 3.6 We will often find it useful to denote conditions in
![]() $\mathbb {R}_\xi $
by the letters
$\mathbb {R}_\xi $
by the letters
![]() $u,v$
and w. If
$u,v$
and w. If
![]() $u\in \mathbb {R}_\xi $
, we write
$u\in \mathbb {R}_\xi $
, we write
![]() $p_u$
and
$p_u$
and
![]() $f_u$
to denote the objects so that
$f_u$
to denote the objects so that
![]() $u=( p_u,f_u)$
. Furthermore, if
$u=( p_u,f_u)$
. Furthermore, if
![]() $\zeta \leq \xi $
, then we write
$\zeta \leq \xi $
, then we write
![]() $u\upharpoonright \zeta $
to denote the pair
$u\upharpoonright \zeta $
to denote the pair
![]() $(p_u,f_u\upharpoonright \zeta )$
, which restricts the length. This should not be confused with
$(p_u,f_u\upharpoonright \zeta )$
, which restricts the length. This should not be confused with
![]() $u\upharpoonright M_\alpha = (\varphi ^{M_\alpha }(p),f\upharpoonright M_\alpha )$
from Definition 3.5, which restricts the height.
$u\upharpoonright M_\alpha = (\varphi ^{M_\alpha }(p),f\upharpoonright M_\alpha )$
from Definition 3.5, which restricts the height.
The following definitions of
![]() $\#$
and
$\#$
and
![]() $*$
are taken from [Reference Laver and Shelah30] and modified to the current presentation. The dual residue property defined in (2) of the upcoming definition is the natural translation into the current situation of the statement that “
$*$
are taken from [Reference Laver and Shelah30] and modified to the current presentation. The dual residue property defined in (2) of the upcoming definition is the natural translation into the current situation of the statement that “
![]() $\#$
implies
$\#$
implies
![]() $*$
” at
$*$
” at
![]() $\alpha $
from [Reference Laver and Shelah30].
$\alpha $
from [Reference Laver and Shelah30].
Definition 3.7 Suppose that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
, that
$\rho $
, that
![]() $\alpha \in \operatorname {dom}(\vec {M})$
, and that
$\alpha \in \operatorname {dom}(\vec {M})$
, and that
![]() $\zeta \leq \rho $
is in
$\zeta \leq \rho $
is in
![]() $M_\alpha $
.
$M_\alpha $
.
-
(1) Fix conditions
 $u,v\in \mathbb {R}_\zeta $
and
$u,v\in \mathbb {R}_\zeta $
and
 $w\in \mathbb {R}_\zeta \cap M_\alpha $
. Fix a residue pair
$w\in \mathbb {R}_\zeta \cap M_\alpha $
. Fix a residue pair
 $\langle p^*(M_\alpha ), \varphi ^{M_\alpha }\rangle $
for
$\langle p^*(M_\alpha ), \varphi ^{M_\alpha }\rangle $
for
 $(M_\alpha ,\mathbb {P}^*)$
.
$(M_\alpha ,\mathbb {P}^*)$
.-
(a) We say that
holds if $$ \begin{align*}\#^\zeta_{\varphi^{M_\alpha}}(u,v,w) \end{align*} $$
$$ \begin{align*}\#^\zeta_{\varphi^{M_\alpha}}(u,v,w) \end{align*} $$
 $u,v\in D(\varphi ^{M_\alpha },\zeta )$
and
$u,v\in D(\varphi ^{M_\alpha },\zeta )$
and
 $u\upharpoonright M_\alpha =^*w=^*v\upharpoonright M_\alpha $
.Footnote
2
$u\upharpoonright M_\alpha =^*w=^*v\upharpoonright M_\alpha $
.Footnote
2
-
(b) We say that
holds if $$ \begin{align*}*^\zeta_{\varphi^{M_\alpha}}(u,v,w) \end{align*} $$
$$ \begin{align*}*^\zeta_{\varphi^{M_\alpha}}(u,v,w) \end{align*} $$
 $u,v\in D(\varphi ^{M_\alpha },\zeta )$
and if
$u,v\in D(\varphi ^{M_\alpha },\zeta )$
and if
 $w\geq u\upharpoonright M_\alpha ,v\upharpoonright M_\alpha $
is a dual residue for u and v (see Definition 2.2).Footnote
3
$w\geq u\upharpoonright M_\alpha ,v\upharpoonright M_\alpha $
is a dual residue for u and v (see Definition 2.2).Footnote
3
-
-
(2) We say that
 $\mathbb {R}_\zeta $
satisfies the dual residue property at
$\mathbb {R}_\zeta $
satisfies the dual residue property at
 $M_\alpha $
if for any residue pair
$M_\alpha $
if for any residue pair
 $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
 $(M_\alpha ,\mathbb {P}^*)$
and any conditions
$(M_\alpha ,\mathbb {P}^*)$
and any conditions
 $u,v,w$
so that
$u,v,w$
so that
 $\#^\zeta _{\varphi ^{M_\alpha }}(u,v,w)$
holds, there exists
$\#^\zeta _{\varphi ^{M_\alpha }}(u,v,w)$
holds, there exists
 $w^*\geq _{\mathbb {R}_\zeta \cap M_\alpha } w$
so that
$w^*\geq _{\mathbb {R}_\zeta \cap M_\alpha } w$
so that
 $*^\zeta _{\varphi ^{M_\alpha }}(u,v,w^*)$
holds.
$*^\zeta _{\varphi ^{M_\alpha }}(u,v,w^*)$
holds.
Lemma 3.4 Suppose that
![]() $*^\zeta _{\varphi ^{M_\alpha }}(u,v,w)$
holds and that D is dense and countably
$*^\zeta _{\varphi ^{M_\alpha }}(u,v,w)$
holds and that D is dense and countably
![]() $=^*$
-closed in
$=^*$
-closed in
![]() $\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
. Then:
$\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
. Then:
-
(1) there exist
 $u'\geq u$
,
$u'\geq u$
,
 $v'\geq v$
with
$v'\geq v$
with
 $u',v'\in D$
and there exists
$u',v'\in D$
and there exists
 $w'\geq w$
so that
$w'\geq w$
so that
 $u'\upharpoonright M_\alpha \geq w$
,
$u'\upharpoonright M_\alpha \geq w$
,
 $v'\upharpoonright M_\alpha \geq w$
, and
$v'\upharpoonright M_\alpha \geq w$
, and
 $*^\zeta _{\varphi ^{M_\alpha }}(u',v',w')$
holds; and
$*^\zeta _{\varphi ^{M_\alpha }}(u',v',w')$
holds; and -
(2) there exist
 $u^*\geq u$
and
$u^*\geq u$
and
 $v^*\geq v$
with
$v^*\geq v$
with
 $u^*,v^*\in D$
, and there exists
$u^*,v^*\in D$
, and there exists
 $w^*\geq w$
so that
$w^*\geq w$
so that
 $\#^\zeta _{\varphi ^{M_\alpha }}(u^*,v^*,w^*)$
holds.
$\#^\zeta _{\varphi ^{M_\alpha }}(u^*,v^*,w^*)$
holds.
Proof First, define E to be the set of conditions s in
![]() $\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
so that
$\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
so that
![]() $s\in D(\varphi ^{M_\alpha },\zeta )\cap D$
and so that either
$s\in D(\varphi ^{M_\alpha },\zeta )\cap D$
and so that either
![]() $s\upharpoonright M_\alpha \geq w$
or
$s\upharpoonright M_\alpha \geq w$
or
![]() $s\upharpoonright M_\alpha $
is incompatible with w; then E is dense in
$s\upharpoonright M_\alpha $
is incompatible with w; then E is dense in
![]() $\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
. Now, fix a V-generic filter
$\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
. Now, fix a V-generic filter
![]() $\bar {G}$
over
$\bar {G}$
over
![]() $\mathbb {R}_\zeta \cap M_\alpha $
containing w, and note that u and v are in
$\mathbb {R}_\zeta \cap M_\alpha $
containing w, and note that u and v are in
![]() $(\mathbb {R}_\zeta /(p^*(M_\alpha ),{0_{\dot {\mathbb {S}}_\zeta })})/\bar {G}$
. By Lemma 2.4(2), we can find
$(\mathbb {R}_\zeta /(p^*(M_\alpha ),{0_{\dot {\mathbb {S}}_\zeta })})/\bar {G}$
. By Lemma 2.4(2), we can find
![]() $u'\geq u$
and
$u'\geq u$
and
![]() $v'\geq v$
so that
$v'\geq v$
so that
![]() $u',v'$
are in E as well as in
$u',v'$
are in E as well as in
![]() $(\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\bar {G}$
. We next observe that
$(\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\bar {G}$
. We next observe that
![]() $u'\upharpoonright M_\alpha \in \bar {G}$
. Indeed, since
$u'\upharpoonright M_\alpha \in \bar {G}$
. Indeed, since
![]() $u'\in D(\varphi ^{M_\alpha },\zeta )$
,
$u'\in D(\varphi ^{M_\alpha },\zeta )$
,
![]() $u'\upharpoonright M_\alpha $
is a condition in
$u'\upharpoonright M_\alpha $
is a condition in
![]() $\mathbb {R}_\zeta \cap M_\alpha $
. In addition, since
$\mathbb {R}_\zeta \cap M_\alpha $
. In addition, since
![]() $u'\in (\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\bar {G}$
and
$u'\in (\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\bar {G}$
and
![]() $u'\geq u'\upharpoonright M_\alpha $
, we have that
$u'\geq u'\upharpoonright M_\alpha $
, we have that
![]() $u'\upharpoonright M_\alpha $
(a condition) is compatible with every condition in
$u'\upharpoonright M_\alpha $
(a condition) is compatible with every condition in
![]() $\bar {G}$
. Thus,
$\bar {G}$
. Thus,
![]() $u'\upharpoonright M_\alpha \in \bar {G}$
. However, by definition of E, and since
$u'\upharpoonright M_\alpha \in \bar {G}$
. However, by definition of E, and since
![]() $w\in \bar {G}$
,
$w\in \bar {G}$
,
![]() $u'\upharpoonright M_\alpha $
must extend w. A symmetric argument shows that
$u'\upharpoonright M_\alpha $
must extend w. A symmetric argument shows that
![]() $v'\upharpoonright M_\alpha \geq w$
.
$v'\upharpoonright M_\alpha \geq w$
.
Now, let
![]() $w'\in \bar {G}$
be a condition extending w which forces that
$w'\in \bar {G}$
be a condition extending w which forces that
![]() $u',v'$
are in
$u',v'$
are in
![]() $(\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\dot {\bar {G}}$
. By Lemma 2.3, we have that
$(\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\dot {\bar {G}}$
. By Lemma 2.3, we have that
![]() $*^\zeta _{\varphi ^{M_\alpha }}(u',v',w')$
holds. Since
$*^\zeta _{\varphi ^{M_\alpha }}(u',v',w')$
holds. Since
![]() $u'\upharpoonright M_\alpha $
and
$u'\upharpoonright M_\alpha $
and
![]() $v'\upharpoonright M_\alpha $
both extend w, this completes the proof of (1).
$v'\upharpoonright M_\alpha $
both extend w, this completes the proof of (1).
For (2), suppose that we are given conditions
![]() $u_0,v_0$
, and
$u_0,v_0$
, and
![]() $w_0$
so that
$w_0$
so that
![]() $*^\zeta _{\varphi ^{M_\alpha }}(u_0,v_0,w_0)$
holds. By repeatedly applying (1), we may define a coordinatewise increasing sequence
$*^\zeta _{\varphi ^{M_\alpha }}(u_0,v_0,w_0)$
holds. By repeatedly applying (1), we may define a coordinatewise increasing sequence
![]() $\langle \langle u_n,v_n,w_n\rangle :n\in \omega \rangle $
so that for all
$\langle \langle u_n,v_n,w_n\rangle :n\in \omega \rangle $
so that for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $u_{n+1}\geq u_n$
and
$u_{n+1}\geq u_n$
and
![]() $v_{n+1}\geq v_n$
;
$v_{n+1}\geq v_n$
;
![]() $u_{n+1}\upharpoonright M_\alpha \geq w_n$
and
$u_{n+1}\upharpoonright M_\alpha \geq w_n$
and
![]() $v_{n+1}\upharpoonright M_\alpha \geq w_n$
; and
$v_{n+1}\upharpoonright M_\alpha \geq w_n$
; and
![]() $*^\zeta _{\varphi ^{M_\alpha }}(u_n,v_n,w_n)$
holds. Let
$*^\zeta _{\varphi ^{M_\alpha }}(u_n,v_n,w_n)$
holds. Let
![]() $u^*$
be a sup of
$u^*$
be a sup of
![]() $\langle u_n:n\in \omega \rangle $
, and let
$\langle u_n:n\in \omega \rangle $
, and let
![]() $v^*$
and
$v^*$
and
![]() $w^*$
be defined similarly. Since
$w^*$
be defined similarly. Since
![]() $*^\zeta _{\varphi ^{M_\alpha }}(u_n,v_n,w_n)$
holds for each n, by definition, we have that
$*^\zeta _{\varphi ^{M_\alpha }}(u_n,v_n,w_n)$
holds for each n, by definition, we have that
![]() $w_n\geq u_n\upharpoonright M_\alpha ,v_n\upharpoonright M_\alpha $
. Therefore, the sequences
$w_n\geq u_n\upharpoonright M_\alpha ,v_n\upharpoonright M_\alpha $
. Therefore, the sequences
![]() $\langle u_n\upharpoonright M_\alpha :n\in \omega \rangle $
and
$\langle u_n\upharpoonright M_\alpha :n\in \omega \rangle $
and
![]() $\langle v_n\upharpoonright M_\alpha :n\in \omega \rangle $
are each intertwined with
$\langle v_n\upharpoonright M_\alpha :n\in \omega \rangle $
are each intertwined with
![]() $\langle w_n:n\in \omega \rangle $
, and consequently, they have suprema which are
$\langle w_n:n\in \omega \rangle $
, and consequently, they have suprema which are
![]() $=^*$
-related. It follows by the continuity of
$=^*$
-related. It follows by the continuity of
![]() $\varphi ^{M_\alpha }$
that
$\varphi ^{M_\alpha }$
that
![]() $\#^\zeta _{\varphi ^{M_\alpha }}(u^*,v^*,w^*)$
holds.▪
$\#^\zeta _{\varphi ^{M_\alpha }}(u^*,v^*,w^*)$
holds.▪
Suppose that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
, that
$\rho $
, that
![]() $\alpha \in \operatorname {dom}(\vec {M})$
, and that
$\alpha \in \operatorname {dom}(\vec {M})$
, and that
![]() $\zeta \in M_\alpha \cap \rho $
. Fix
$\zeta \in M_\alpha \cap \rho $
. Fix
![]() $\theta \in (\kappa \setminus \alpha ) \times \omega _1$
, a node in the tree
$\theta \in (\kappa \setminus \alpha ) \times \omega _1$
, a node in the tree
![]() $\dot {T}_\zeta $
of level greater than or equal to
$\dot {T}_\zeta $
of level greater than or equal to
![]() $\alpha $
.
$\alpha $
.
Let
![]() $\dot {b}_\zeta (\theta ,\alpha )$
denote the
$\dot {b}_\zeta (\theta ,\alpha )$
denote the
![]() $\mathbb {R}_\zeta $
-name for
$\mathbb {R}_\zeta $
-name for
![]() $\left \{\bar {\theta }\in \alpha \times \omega _1:\bar {\theta }<_{\dot {T}_\zeta }\theta \right \}$
. By Proposition 3.2(2), the condition
$\left \{\bar {\theta }\in \alpha \times \omega _1:\bar {\theta }<_{\dot {T}_\zeta }\theta \right \}$
. By Proposition 3.2(2), the condition
![]() $(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
forces that
$(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta })$
forces that
![]() $\dot {b}_\zeta (\theta ,\alpha )$
is a cofinal branch through
$\dot {b}_\zeta (\theta ,\alpha )$
is a cofinal branch through
![]() $(\dot {T}_\zeta \cap M_\alpha )[\dot {G}_{\mathbb {R}_\zeta \cap M_\alpha }]$
. Note that by Proposition 3.2 and the definition of pre-splitting configuration,
$(\dot {T}_\zeta \cap M_\alpha )[\dot {G}_{\mathbb {R}_\zeta \cap M_\alpha }]$
. Note that by Proposition 3.2 and the definition of pre-splitting configuration,
![]() $(\dot {T}_\zeta \cap M_\alpha )[G_{\mathbb {R}_\zeta \cap M_\alpha }]$
is an Aronszajn tree on
$(\dot {T}_\zeta \cap M_\alpha )[G_{\mathbb {R}_\zeta \cap M_\alpha }]$
is an Aronszajn tree on
![]() $\alpha $
in the V-generic extension
$\alpha $
in the V-generic extension
![]() $V[G_{\mathbb {R}_\zeta \cap M_\alpha }]$
over
$V[G_{\mathbb {R}_\zeta \cap M_\alpha }]$
over
![]() $\mathbb {R}_\zeta \cap M_\alpha $
. In light of this, we make the following definition.
$\mathbb {R}_\zeta \cap M_\alpha $
. In light of this, we make the following definition.
Definition 3.8 Let
![]() $\zeta <\rho $
,
$\zeta <\rho $
,
![]() $\alpha <\kappa $
, and
$\alpha <\kappa $
, and
![]() $\langle \theta ,\tau \rangle $
be a pair of tree nodes (possibly equal) at or above level
$\langle \theta ,\tau \rangle $
be a pair of tree nodes (possibly equal) at or above level
![]() $\alpha $
, which we view as nodes in the tree
$\alpha $
, which we view as nodes in the tree
![]() $\dot {T}_\zeta $
. We say that two conditions u and v in
$\dot {T}_\zeta $
. We say that two conditions u and v in
![]() $\mathbb {R}_\zeta $
split
$\mathbb {R}_\zeta $
split
![]() $\langle \theta ,\tau \rangle $
below
$\langle \theta ,\tau \rangle $
below
![]() $\alpha $
in
$\alpha $
in
![]() $\dot {T}_\zeta $
if there exist a level
$\dot {T}_\zeta $
if there exist a level
![]() $\bar {\alpha }<\alpha $
and distinct nodes
$\bar {\alpha }<\alpha $
and distinct nodes
![]() $\bar {\theta },\bar {\tau }$
on level
$\bar {\theta },\bar {\tau }$
on level
![]() $\bar {\alpha }$
so that
$\bar {\alpha }$
so that
![]() $u\Vdash \bar {\theta }<_{\dot {T}_\zeta }\theta $
and
$u\Vdash \bar {\theta }<_{\dot {T}_\zeta }\theta $
and
![]() $v\Vdash \bar {\tau }<_{\dot {T}_\zeta }\tau $
. More generally, if
$v\Vdash \bar {\tau }<_{\dot {T}_\zeta }\tau $
. More generally, if
![]() $\zeta \leq \xi <\rho $
and
$\zeta \leq \xi <\rho $
and
![]() $u',v' \in \mathbb {R}_\xi $
, then we say that
$u',v' \in \mathbb {R}_\xi $
, then we say that
![]() $u'$
and
$u'$
and
![]() $v'$
split
$v'$
split
![]() $\langle \theta ,\tau \rangle $
below
$\langle \theta ,\tau \rangle $
below
![]() $\alpha $
in
$\alpha $
in
![]() $\dot {T}_\zeta $
if
$\dot {T}_\zeta $
if
![]() $u = u'\upharpoonright \zeta $
and
$u = u'\upharpoonright \zeta $
and
![]() $v = v'\upharpoonright \zeta $
do.
$v = v'\upharpoonright \zeta $
do.
Lemma 3.5 Suppose that
![]() $\zeta \leq \xi < \rho $
and
$\zeta \leq \xi < \rho $
and
![]() $\mathbb {R}_\xi $
satisfies the dual residue property at some
$\mathbb {R}_\xi $
satisfies the dual residue property at some
![]() $M_\alpha $
, where
$M_\alpha $
, where
![]() $\zeta \in M_\alpha $
(see Definition 3.7). Fix
$\zeta \in M_\alpha $
(see Definition 3.7). Fix
![]() $u,v\in \mathbb {R}_\xi $
so that for some
$u,v\in \mathbb {R}_\xi $
so that for some
![]() $w\in \mathbb {R}_\xi \cap M_\alpha $
,
$w\in \mathbb {R}_\xi \cap M_\alpha $
,
![]() $\#^\xi _{\varphi ^{M_\alpha }}(u,v,w)$
. Let
$\#^\xi _{\varphi ^{M_\alpha }}(u,v,w)$
. Let
![]() $\langle \theta ,\tau \rangle $
be a pair of tree nodes (possibly equal) each of which is at or above level
$\langle \theta ,\tau \rangle $
be a pair of tree nodes (possibly equal) each of which is at or above level
![]() $\alpha $
. Then there exist extensions
$\alpha $
. Then there exist extensions
![]() $u^*\geq u$
,
$u^*\geq u$
,
![]() $v^*\geq v$
, and
$v^*\geq v$
, and
![]() $w^*\geq w$
so that
$w^*\geq w$
so that
![]() $\#^\xi _{\varphi ^{M_\alpha }}(u^*,v^*,w^*)$
and so that
$\#^\xi _{\varphi ^{M_\alpha }}(u^*,v^*,w^*)$
and so that
![]() $u^*$
and
$u^*$
and
![]() $v^*$
split
$v^*$
split
![]() $\langle \theta ,\tau \rangle $
below
$\langle \theta ,\tau \rangle $
below
![]() $\alpha $
in
$\alpha $
in
![]() $\dot {T}_\zeta $
.
$\dot {T}_\zeta $
.
Proof Since
![]() $\mathbb {R}_\xi $
satisfies the dual residue property at
$\mathbb {R}_\xi $
satisfies the dual residue property at
![]() $M_\alpha $
,
$M_\alpha $
,
![]() $\mathbb {R}_\zeta $
does too, and so we may find some
$\mathbb {R}_\zeta $
does too, and so we may find some
![]() $w'\in \mathbb {R}_\zeta \cap M_\alpha $
so that
$w'\in \mathbb {R}_\zeta \cap M_\alpha $
so that
![]() $w'\geq _{\mathbb {R}_\zeta } w\upharpoonright \zeta $
and
$w'\geq _{\mathbb {R}_\zeta } w\upharpoonright \zeta $
and
![]() $*^\zeta _{\varphi ^{M_\alpha }}(u\upharpoonright \zeta ,v\upharpoonright \zeta ,w')$
. Fix a V-generic filter
$*^\zeta _{\varphi ^{M_\alpha }}(u\upharpoonright \zeta ,v\upharpoonright \zeta ,w')$
. Fix a V-generic filter
![]() $\bar {G}$
over
$\bar {G}$
over
![]() $\mathbb {R}_\zeta \cap M_\alpha $
containing
$\mathbb {R}_\zeta \cap M_\alpha $
containing
![]() $w'$
. As a result,
$w'$
. As a result,
![]() $u\upharpoonright \zeta $
and
$u\upharpoonright \zeta $
and
![]() $v\upharpoonright \zeta $
are in
$v\upharpoonright \zeta $
are in
![]() $(\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\bar {G}$
. By the discussion preceding Definition 3.8, we know that
$(\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\bar {G}$
. By the discussion preceding Definition 3.8, we know that
![]() $u\upharpoonright \zeta $
forces in the quotient that
$u\upharpoonright \zeta $
forces in the quotient that
![]() $\dot {b}_\zeta (\theta ,\alpha )$
is a cofinal branch through
$\dot {b}_\zeta (\theta ,\alpha )$
is a cofinal branch through
![]() $\bar {T}:=(\dot {T}_\zeta \cap M_\alpha )[\bar {G}]$
, which by Proposition 3.2 is an Aronszajn tree on
$\bar {T}:=(\dot {T}_\zeta \cap M_\alpha )[\bar {G}]$
, which by Proposition 3.2 is an Aronszajn tree on
![]() $\alpha $
in
$\alpha $
in
![]() $V[\bar {G}]$
. Consequently, we may find two conditions
$V[\bar {G}]$
. Consequently, we may find two conditions
![]() $u_0,u_1$
which extend
$u_0,u_1$
which extend
![]() $u\upharpoonright \zeta $
in
$u\upharpoonright \zeta $
in
![]() $(\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\bar {G}$
, some level
$(\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\bar {G}$
, some level
![]() $\bar {\alpha }<\alpha $
, and two distinct nodes
$\bar {\alpha }<\alpha $
, and two distinct nodes
![]() $\theta _0,\theta _1$
on level
$\theta _0,\theta _1$
on level
![]() $\bar {\alpha }$
of
$\bar {\alpha }$
of
![]() $\bar {T}$
so that
$\bar {T}$
so that
![]() $u_i$
forces in
$u_i$
forces in
![]() $(\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\bar {G}$
that
$(\mathbb {R}_\zeta /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\zeta }))/\bar {G}$
that
![]() $\theta _i<_{\dot {T}_\zeta }\theta $
. Since
$\theta _i<_{\dot {T}_\zeta }\theta $
. Since
![]() $v\upharpoonright \zeta $
also forces that
$v\upharpoonright \zeta $
also forces that
![]() $\dot {b}_\zeta (\tau ,\alpha )$
is a cofinal branch through
$\dot {b}_\zeta (\tau ,\alpha )$
is a cofinal branch through
![]() $\bar {T}$
, we may find some extension
$\bar {T}$
, we may find some extension
![]() $v_0$
of
$v_0$
of
![]() $v\upharpoonright \zeta $
in the quotient so that
$v\upharpoonright \zeta $
in the quotient so that
![]() $v_0$
decides the
$v_0$
decides the
![]() $<_{\dot {T}_\zeta }$
-predecessor, say
$<_{\dot {T}_\zeta }$
-predecessor, say
![]() $\bar {\tau }$
, of
$\bar {\tau }$
, of
![]() $\tau $
on level
$\tau $
on level
![]() $\bar {\alpha }$
of
$\bar {\alpha }$
of
![]() $\bar {T}$
. As
$\bar {T}$
. As
![]() $\theta _0\neq \theta _1$
, there exists some
$\theta _0\neq \theta _1$
, there exists some
![]() $i\in 2$
so that
$i\in 2$
so that
![]() $\theta _i\neq \bar {\tau }$
. Set
$\theta _i\neq \bar {\tau }$
. Set
![]() $\bar {\theta }=\theta _i$
.
$\bar {\theta }=\theta _i$
.
Now, fix an extension
![]() $w''$
of
$w''$
of
![]() $w'$
in
$w'$
in
![]() $\bar {G}$
so that
$\bar {G}$
so that
![]() $w''$
forces the following statements: (i)
$w''$
forces the following statements: (i)
![]() $u_i,v_0$
are in the quotient; (ii)
$u_i,v_0$
are in the quotient; (ii)
![]() $u_i$
forces in the quotient that
$u_i$
forces in the quotient that
![]() $\bar {\theta }<_{\dot {T}_\zeta }\theta $
; and (iii)
$\bar {\theta }<_{\dot {T}_\zeta }\theta $
; and (iii)
![]() $v_0$
forces in the quotient that
$v_0$
forces in the quotient that
![]() $\bar {\tau }<_{\dot {T}_\zeta }\tau $
.
$\bar {\tau }<_{\dot {T}_\zeta }\tau $
.
By two applications of Lemma 2.4(3), we may find conditions
![]() $\bar {u},\bar {v}$
in the quotient so that
$\bar {u},\bar {v}$
in the quotient so that
![]() $\bar {u}$
extends
$\bar {u}$
extends
![]() $u_i$
and
$u_i$
and
![]() $w''$
, so that
$w''$
, so that
![]() $\bar {v}$
extends
$\bar {v}$
extends
![]() $v_0$
and
$v_0$
and
![]() $w''$
, and so that
$w''$
, and so that
![]() $\bar {u},\bar {v}\in D(\varphi ^{M_\alpha },\zeta )$
.
$\bar {u},\bar {v}\in D(\varphi ^{M_\alpha },\zeta )$
.
We now see that
![]() $\bar {u}\Vdash _{\mathbb {R}_\zeta }\bar {\theta }<_{\dot {T}_\zeta }\theta $
, since
$\bar {u}\Vdash _{\mathbb {R}_\zeta }\bar {\theta }<_{\dot {T}_\zeta }\theta $
, since
and since
![]() $\bar {u}\geq w'',u_i$
. Similarly,
$\bar {u}\geq w'',u_i$
. Similarly,
![]() $\bar {v}\Vdash _{\mathbb {R}_\zeta }\bar {\tau }<_{\dot {T}_\zeta }\tau $
.
$\bar {v}\Vdash _{\mathbb {R}_\zeta }\bar {\tau }<_{\dot {T}_\zeta }\tau $
.
Finally, let
![]() $\bar {w}\geq w''$
be a condition in
$\bar {w}\geq w''$
be a condition in
![]() $\bar {G}$
which forces that
$\bar {G}$
which forces that
![]() $\bar {u}$
and
$\bar {u}$
and
![]() $\bar {v}$
are in the quotient, so that by Lemma 2.3,
$\bar {v}$
are in the quotient, so that by Lemma 2.3,
![]() $*^\zeta _{\varphi ^{M_\alpha }}(\bar {u},\bar {v},\bar {w})$
holds. By Lemma 3.4, we can find some
$*^\zeta _{\varphi ^{M_\alpha }}(\bar {u},\bar {v},\bar {w})$
holds. By Lemma 3.4, we can find some
![]() $\bar {u}^*\geq \bar {u}$
,
$\bar {u}^*\geq \bar {u}$
,
![]() $\bar {v}^*\geq \bar {v}$
, and
$\bar {v}^*\geq \bar {v}$
, and
![]() $\bar {w}^*\geq w$
so that
$\bar {w}^*\geq w$
so that
![]() $\#^\zeta _{\varphi ^{M_\alpha }}(\bar {u}^*,\bar {v}^*,\bar {w}^*)$
holds. Now, let
$\#^\zeta _{\varphi ^{M_\alpha }}(\bar {u}^*,\bar {v}^*,\bar {w}^*)$
holds. Now, let
![]() $u^*$
be the condition where
$u^*$
be the condition where
![]() $p_{u^*}=p_{\bar {u}^*}$
, and where
$p_{u^*}=p_{\bar {u}^*}$
, and where
![]() $f_{u^*}=f_{\bar {u}^*}\,^{\frown } f_u\upharpoonright [\zeta ,\xi )$
. Let
$f_{u^*}=f_{\bar {u}^*}\,^{\frown } f_u\upharpoonright [\zeta ,\xi )$
. Let
![]() $v^*$
and
$v^*$
and
![]() $w^*$
be defined similarly. Then
$w^*$
be defined similarly. Then
![]() $\#^\xi _{\varphi ^{M_\alpha }}(u^*,v^*,w^*)$
, and
$\#^\xi _{\varphi ^{M_\alpha }}(u^*,v^*,w^*)$
, and
![]() $u^*$
and
$u^*$
and
![]() $v^*$
split
$v^*$
split
![]() $\langle \theta ,\tau \rangle $
below
$\langle \theta ,\tau \rangle $
below
![]() $\alpha $
.▪
$\alpha $
.▪
One of the most important uses of the dual residue property is to obtain splitting pairs of conditions. Obtaining such conditions will also crucially use the “exactness” conditions of Definition 2.8.
Definition 3.9 Suppose that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
.
$\rho $
.
-
(1) Let
 $\alpha \in \operatorname {dom}(\vec {M})$
and
$\alpha \in \operatorname {dom}(\vec {M})$
and
 $\xi \in M_\alpha \cap \rho $
. Fix a residue pair
$\xi \in M_\alpha \cap \rho $
. Fix a residue pair
 $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
 $(M_\alpha ,\mathbb {P}^*)$
and conditions
$(M_\alpha ,\mathbb {P}^*)$
and conditions
 $u,v\in \mathbb {R}_\xi $
. We say that u and v are a splitting pair for
$u,v\in \mathbb {R}_\xi $
. We say that u and v are a splitting pair for
 $(\varphi ^{M_\alpha },\xi )$
if:
$(\varphi ^{M_\alpha },\xi )$
if:-
• for some
 $w\in \mathbb {R}_\xi \cap M_\alpha $
,
$w\in \mathbb {R}_\xi \cap M_\alpha $
,
 $\#^\xi _{\varphi ^{M_\alpha }}(u,v,w)$
; and
$\#^\xi _{\varphi ^{M_\alpha }}(u,v,w)$
; and -
• for any
 $\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_u)\cap \operatorname {dom}(f_v)\cap M_\alpha $
and any
$\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_u)\cap \operatorname {dom}(f_v)\cap M_\alpha $
and any
 $ \langle \theta ,\tau \rangle \in (f_u(\zeta ,\nu ))\times (f_v(\zeta ,\nu )), $
both at or above level,
$ \langle \theta ,\tau \rangle \in (f_u(\zeta ,\nu ))\times (f_v(\zeta ,\nu )), $
both at or above level,
 $\alpha $
, u, and v split
$\alpha $
, u, and v split
 $\langle \theta ,\tau \rangle $
below
$\langle \theta ,\tau \rangle $
below
 $\alpha $
in
$\alpha $
in
 $\dot {T}_\zeta $
.
$\dot {T}_\zeta $
.
-
-
(2) Given fixed enumerations
 $f_u(\zeta ,\nu )\backslash (\alpha \times \omega _1) = \{ \theta _n \mid n < \omega \}$
and
$f_u(\zeta ,\nu )\backslash (\alpha \times \omega _1) = \{ \theta _n \mid n < \omega \}$
and
 $f_v(\zeta ,\nu )\backslash (\alpha \times \omega _1) = \{ \tau _m \mid m < \omega \}$
(possibly with repetitions in the case the sets are finite, nonempty), we define a splitting function to be a function
$f_v(\zeta ,\nu )\backslash (\alpha \times \omega _1) = \{ \tau _m \mid m < \omega \}$
(possibly with repetitions in the case the sets are finite, nonempty), we define a splitting function to be a function
 $\Sigma $
with domainFootnote
4
so that for any
$\Sigma $
with domainFootnote
4
so that for any $$ \begin{align*}\operatorname{dom}(\Sigma)=(\operatorname{dom}(f_u)\cap\operatorname{dom}(f_v)\cap M_\alpha)\times\omega\times\omega, \end{align*} $$
$$ \begin{align*}\operatorname{dom}(\Sigma)=(\operatorname{dom}(f_u)\cap\operatorname{dom}(f_v)\cap M_\alpha)\times\omega\times\omega, \end{align*} $$
 $\langle \zeta ,\nu ,m,n\rangle \in \operatorname {dom}(\Sigma )$
,
$\langle \zeta ,\nu ,m,n\rangle \in \operatorname {dom}(\Sigma )$
,
 $\Sigma (\zeta ,\nu ,m,n)$
is a pair
$\Sigma (\zeta ,\nu ,m,n)$
is a pair
 $\langle \bar {\theta },\bar {\tau }\rangle $
of tree nodes satisfying Definition 3.8 with respect to
$\langle \bar {\theta },\bar {\tau }\rangle $
of tree nodes satisfying Definition 3.8 with respect to
 $\langle \theta _m,\tau _n\rangle $
. We will denote
$\langle \theta _m,\tau _n\rangle $
. We will denote
 $\bar {\theta }$
by
$\bar {\theta }$
by
 $\Sigma (\zeta ,\nu ,m,n)(L)$
and
$\Sigma (\zeta ,\nu ,m,n)(L)$
and
 $\bar {\tau }$
by
$\bar {\tau }$
by
 $\Sigma (\zeta ,\nu ,m,n)(R)$
.
$\Sigma (\zeta ,\nu ,m,n)(R)$
.
Remark 3.6 Let
![]() $\Sigma $
be as in Definition 3.9.
$\Sigma $
be as in Definition 3.9.
-
(1) We emphasize the fact that if
 $\langle \zeta ,\nu ,m,n\rangle \in \operatorname {dom}(\Sigma )$
, then are two distinct tree nodes on the same level. We will usually suppress explicit mention of the level.
$\langle \zeta ,\nu ,m,n\rangle \in \operatorname {dom}(\Sigma )$
, then are two distinct tree nodes on the same level. We will usually suppress explicit mention of the level. $$ \begin{align*}\Sigma(\zeta,\nu,m,n)(L)\neq\Sigma(\zeta,\nu,m,n)(R) \end{align*} $$
$$ \begin{align*}\Sigma(\zeta,\nu,m,n)(L)\neq\Sigma(\zeta,\nu,m,n)(R) \end{align*} $$
-
(2) Any splitting function
 $\Sigma $
is a member of
$\Sigma $
is a member of
 $M_\alpha $
since
$M_\alpha $
since
 $M_\alpha $
is countably closed and since
$M_\alpha $
is countably closed and since
 $\Sigma $
maps from a countable subset of
$\Sigma $
maps from a countable subset of
 $M_\alpha $
into
$M_\alpha $
into
 $M_\alpha $
.
$M_\alpha $
. -
(3) We only require the splitting pair in Definition 3.9 to split nodes coming from coordinates which are members of
 $M_\alpha $
. As we will see from Lemma 3.8 and later thinning out arguments, this is sufficient for our purposes.
$M_\alpha $
. As we will see from Lemma 3.8 and later thinning out arguments, this is sufficient for our purposes.
Now, we are ready to state our second inductive hypothesis, the point of which is to provide plenty of instances of the dual residue property. We will assume the second inductive hypothesis for the rest of the section. We again recall the filter
![]() $\mathcal {F}$
and its dual ideal
$\mathcal {F}$
and its dual ideal
![]() $\mathcal {I}$
from Definition 2.8.
$\mathcal {I}$
from Definition 2.8.
Inductive Hypothesis II: Let
![]() $\xi <\rho $
, and suppose that
$\xi <\rho $
, and suppose that
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\mathbb {R}_\xi $
-suitable. Then there is an
$\mathbb {R}_\xi $
-suitable. Then there is an
![]() $A\subseteq \operatorname {dom}(\vec {M})$
with
$A\subseteq \operatorname {dom}(\vec {M})$
with
![]() $A\in \mathcal {I}$
so that for all
$A\in \mathcal {I}$
so that for all
![]() $\alpha \in \operatorname {dom}(\vec {M})\backslash A$
,
$\alpha \in \operatorname {dom}(\vec {M})\backslash A$
,
![]() $\mathbb {R}_\xi $
satisfies the dual residue property at
$\mathbb {R}_\xi $
satisfies the dual residue property at
![]() $M_\alpha $
.
$M_\alpha $
.
Now, we move to the main part of the proof that
![]() $\mathbb {P}^*$
satisfies Inductive Hypotheses I and II with respect to
$\mathbb {P}^*$
satisfies Inductive Hypotheses I and II with respect to
![]() $\rho $
. After a bit more setup, we will verify Inductive Hypothesis I for
$\rho $
. After a bit more setup, we will verify Inductive Hypothesis I for
![]() $\rho $
and then use this to verify Inductive Hypothesis II at
$\rho $
and then use this to verify Inductive Hypothesis II at
![]() $\rho $
.
$\rho $
.
The following lemma amalgamates instance of the second induction hypothesis below
![]() $\rho $
, stating that if
$\rho $
, stating that if
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\rho $
-suitable, then for almost all
$\rho $
-suitable, then for almost all
![]() $\alpha \in \operatorname {dom}(\vec {M})$
and all
$\alpha \in \operatorname {dom}(\vec {M})$
and all
![]() $\xi \in M_\alpha \cap \rho $
,
$\xi \in M_\alpha \cap \rho $
,
![]() $\mathbb {R}_\xi $
satisfies the dual residue property at
$\mathbb {R}_\xi $
satisfies the dual residue property at
![]() $M_\alpha $
. However, we note that the following lemma is far from showing that the second induction hypothesis holds at
$M_\alpha $
. However, we note that the following lemma is far from showing that the second induction hypothesis holds at
![]() $\rho $
itself, only asserting (roughly) that it holds up to
$\rho $
itself, only asserting (roughly) that it holds up to
![]() $\rho $
. The proof involves a standard diagonal union, using the normality of
$\rho $
. The proof involves a standard diagonal union, using the normality of
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Lemma 3.7 Suppose that
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\mathbb {R}_\rho $
-suitable. Then there is an
$\mathbb {R}_\rho $
-suitable. Then there is an
![]() $A\subseteq \operatorname {dom}(\vec {M})$
with
$A\subseteq \operatorname {dom}(\vec {M})$
with
![]() $A\in \mathcal {I}$
so that for all
$A\in \mathcal {I}$
so that for all
![]() $\alpha \in \operatorname {dom}(\vec {M})\backslash A$
and all
$\alpha \in \operatorname {dom}(\vec {M})\backslash A$
and all
![]() $\xi \in M_\alpha \cap \rho $
,
$\xi \in M_\alpha \cap \rho $
,
![]() $\mathbb {R}_\xi $
satisfies the dual residue property at
$\mathbb {R}_\xi $
satisfies the dual residue property at
![]() $M_\alpha $
.
$M_\alpha $
.
Proof Fix
![]() $\vec {M}$
which is
$\vec {M}$
which is
![]() $\mathbb {R}_\rho $
-suitable. If
$\mathbb {R}_\rho $
-suitable. If
![]() $\rho <\kappa $
, then the lemma follows by taking the union of
$\rho <\kappa $
, then the lemma follows by taking the union of
![]() $< \kappa $
-many sets in
$< \kappa $
-many sets in
![]() $\mathcal {I}$
which witness the second induction hypothesis below
$\mathcal {I}$
which witness the second induction hypothesis below
![]() $\rho $
. Suppose, then, that
$\rho $
. Suppose, then, that
![]() $\rho \geq \kappa $
, and let
$\rho \geq \kappa $
, and let
![]() $h:\kappa \longrightarrow \rho $
be the
$h:\kappa \longrightarrow \rho $
be the
![]() $\lhd $
-least bijection from
$\lhd $
-least bijection from
![]() $\kappa $
onto
$\kappa $
onto
![]() $\rho $
. Note that h is in
$\rho $
. Note that h is in
![]() $M_\alpha $
for all
$M_\alpha $
for all
![]() $\alpha \in \operatorname {dom}(\vec {M})$
(since
$\alpha \in \operatorname {dom}(\vec {M})$
(since
![]() $\rho $
is an element of
$\rho $
is an element of
![]() $M_\alpha $
) and that for each such
$M_\alpha $
) and that for each such
![]() $\alpha $
,
$\alpha $
,
![]() $M_\alpha \cap \rho =h[M_\alpha \cap \kappa ]$
. Next, observe that for all
$M_\alpha \cap \rho =h[M_\alpha \cap \kappa ]$
. Next, observe that for all
![]() $\xi <\rho $
, a tail of the sequence
$\xi <\rho $
, a tail of the sequence
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\mathbb {R}_\xi $
-suitable, since a tail of this sequence contains
$\mathbb {R}_\xi $
-suitable, since a tail of this sequence contains
![]() $\xi $
as an element and since each model on
$\xi $
as an element and since each model on
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\mathbb {R}_\rho $
-suitable.
$\mathbb {R}_\rho $
-suitable.
For each
![]() $\xi <\rho $
, we may then find
$\xi <\rho $
, we may then find
![]() $A_\xi \in \mathcal {I}$
so that for all
$A_\xi \in \mathcal {I}$
so that for all
![]() $\alpha \in \operatorname {dom}(\vec {M})\backslash A_\xi $
,
$\alpha \in \operatorname {dom}(\vec {M})\backslash A_\xi $
,
![]() $M_\alpha $
is
$M_\alpha $
is
![]() $\mathbb {R}_\xi $
-suitable and so that
$\mathbb {R}_\xi $
-suitable and so that
![]() $\mathbb {R}_\xi $
satisfies the dual residue property at
$\mathbb {R}_\xi $
satisfies the dual residue property at
![]() $M_\alpha $
. For each
$M_\alpha $
. For each
![]() $\nu <\kappa $
, let
$\nu <\kappa $
, let
![]() $B_\nu :=A_{h(\nu )}$
, and let
$B_\nu :=A_{h(\nu )}$
, and let
![]() $B:=\nabla _{\nu <\kappa }B_\nu =\left \{\beta <\kappa :(\exists \nu <\beta )\,[\beta \in B_\nu ]\right \}$
.
$B:=\nabla _{\nu <\kappa }B_\nu =\left \{\beta <\kappa :(\exists \nu <\beta )\,[\beta \in B_\nu ]\right \}$
.
![]() $B\in \mathcal {I}$
since
$B\in \mathcal {I}$
since
![]() $\mathcal {I}$
is a normal ideal.
$\mathcal {I}$
is a normal ideal.
We now claim that for all
![]() $\alpha \in \operatorname {dom}(\vec {M})$
and all
$\alpha \in \operatorname {dom}(\vec {M})$
and all
![]() $\xi \in M_\alpha \cap \rho $
,
$\xi \in M_\alpha \cap \rho $
,
![]() $M_\alpha $
is
$M_\alpha $
is
![]() $\mathbb {R}_\xi $
-suitable and
$\mathbb {R}_\xi $
-suitable and
![]() $\mathbb {R}_\xi $
satisfies the dual residue property at
$\mathbb {R}_\xi $
satisfies the dual residue property at
![]() $M_\alpha $
. So let such
$M_\alpha $
. So let such
![]() $\alpha $
and
$\alpha $
and
![]() $\xi $
be given.
$\xi $
be given.
![]() $\xi \in M_\alpha \cap \rho $
, and hence
$\xi \in M_\alpha \cap \rho $
, and hence
![]() $\xi =h(\bar {\nu })$
for some
$\xi =h(\bar {\nu })$
for some
![]() $\bar {\nu }<\alpha $
. However,
$\bar {\nu }<\alpha $
. However,
![]() $\alpha \notin B$
, and therefore for all
$\alpha \notin B$
, and therefore for all
![]() $\nu <\alpha $
,
$\nu <\alpha $
,
![]() $\alpha \notin B_\nu =A_{h(\nu )}$
. In particular,
$\alpha \notin B_\nu =A_{h(\nu )}$
. In particular,
![]() $\alpha \notin A_{h(\bar {\nu })}=A_\xi $
. Thus, by choice of
$\alpha \notin A_{h(\bar {\nu })}=A_\xi $
. Thus, by choice of
![]() $A_\xi $
,
$A_\xi $
,
![]() $M_\alpha $
is
$M_\alpha $
is
![]() $\mathbb {R}_\xi $
-suitable, and
$\mathbb {R}_\xi $
-suitable, and
![]() $\mathbb {R}_\xi $
satisfies the dual residue property at
$\mathbb {R}_\xi $
satisfies the dual residue property at
![]() $M_\alpha $
.▪
$M_\alpha $
.▪
At important parts of the following proofs, we will need to understand the circumstances under which we can amalgamate conditions in
![]() $\mathbb {R}_\rho $
, and in particular, in
$\mathbb {R}_\rho $
, and in particular, in
![]() $\dot {\mathbb {S}}_\rho .$
We will often be interested in the following strong sense of amalgamation.
$\dot {\mathbb {S}}_\rho .$
We will often be interested in the following strong sense of amalgamation.
Definition 3.10 Let
![]() $u,v\in \mathbb {R}_\rho $
so that
$u,v\in \mathbb {R}_\rho $
so that
![]() $p_u$
and
$p_u$
and
![]() $p_v$
are compatible in
$p_v$
are compatible in
![]() $\mathbb {P}^*$
. We say that
$\mathbb {P}^*$
. We say that
![]() $f_u$
and
$f_u$
and
![]() $f_v$
are strongly compatible over
$f_v$
are strongly compatible over
![]() $p_u$
and
$p_u$
and
![]() $p_v$
if for any condition
$p_v$
if for any condition
![]() $q\in \mathbb {P}^*$
which extends
$q\in \mathbb {P}^*$
which extends
![]() $p_u$
and
$p_u$
and
![]() $p_v$
, q forces that
$p_v$
, q forces that
![]() $\check {f}_u\cup \check {f}_v\in \dot {\mathbb {S}}_\rho $
.
$\check {f}_u\cup \check {f}_v\in \dot {\mathbb {S}}_\rho $
.
The next lemma gives sufficient conditions under which we may amalgamate conditions in
![]() $\mathbb {R}_\rho $
whose specializing parts are strongly compatible as above.
$\mathbb {R}_\rho $
whose specializing parts are strongly compatible as above.
Lemma 3.8 Suppose that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
, that
$\rho $
, that
![]() $\alpha <\beta $
are in
$\alpha <\beta $
are in
![]() $\operatorname {dom}(\vec {M})$
, and that
$\operatorname {dom}(\vec {M})$
, and that
![]() $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
and
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
and
![]() $\langle p^*(M_\beta ),\varphi ^{M_\beta }\rangle $
are residue pairs for
$\langle p^*(M_\beta ),\varphi ^{M_\beta }\rangle $
are residue pairs for
![]() $(M_\alpha ,\mathbb {P}^*)$
and
$(M_\alpha ,\mathbb {P}^*)$
and
![]() $(M_\beta ,\mathbb {P}^*)$
, respectively. Let
$(M_\beta ,\mathbb {P}^*)$
, respectively. Let
![]() $\langle u_\alpha ,v_\alpha \rangle $
and
$\langle u_\alpha ,v_\alpha \rangle $
and
![]() $\langle u_\beta ,v_\beta \rangle $
be two pairs of conditions in
$\langle u_\beta ,v_\beta \rangle $
be two pairs of conditions in
![]() $\mathbb {R}_\rho $
which satisfy the following:
$\mathbb {R}_\rho $
which satisfy the following:
-
(1)
 $\langle u_\alpha ,v_\alpha \rangle $
is a splitting pair for
$\langle u_\alpha ,v_\alpha \rangle $
is a splitting pair for
 $(\varphi ^{M_\alpha },\rho )$
with splitting function
$(\varphi ^{M_\alpha },\rho )$
with splitting function
 $\Sigma _\alpha $
;
$\Sigma _\alpha $
; -
(2)
 $\langle u_\beta ,v_\beta \rangle $
is a splitting pair for
$\langle u_\beta ,v_\beta \rangle $
is a splitting pair for
 $(\varphi ^{M_\beta },\rho )$
with splitting function
$(\varphi ^{M_\beta },\rho )$
with splitting function
 $\Sigma _\beta $
;
$\Sigma _\beta $
; -
(3)
 $\Sigma _\alpha =\Sigma _\beta $
;
$\Sigma _\alpha =\Sigma _\beta $
; -
(4) there exists
 $w\in M_\alpha $
so that
$w\in M_\alpha $
so that
 $\#^\rho _{\varphi ^{M_\alpha }}(u_\alpha ,v_\alpha ,w)$
and
$\#^\rho _{\varphi ^{M_\alpha }}(u_\alpha ,v_\alpha ,w)$
and
 $\#^\rho _{\varphi ^{M_\beta }}(u_\beta ,v_\beta ,w)$
both hold; and
$\#^\rho _{\varphi ^{M_\beta }}(u_\beta ,v_\beta ,w)$
both hold; and -
(5)
 $u_\alpha ,v_\alpha \in M_\beta $
.
$u_\alpha ,v_\alpha \in M_\beta $
.
Then
![]() $u_\alpha $
and
$u_\alpha $
and
![]() $v_\beta $
are compatible in
$v_\beta $
are compatible in
![]() $\mathbb {R}_\rho $
; in fact,
$\mathbb {R}_\rho $
; in fact,
![]() $f_{u_\alpha }$
is strongly compatible with
$f_{u_\alpha }$
is strongly compatible with
![]() $f_{v_\beta }$
over
$f_{v_\beta }$
over
![]() $p_{u_\alpha }$
and
$p_{u_\alpha }$
and
![]() $p_{v_\beta }$
.
$p_{v_\beta }$
.
Proof We first observe that
![]() $p_{u_\alpha }$
and
$p_{u_\alpha }$
and
![]() $p_{v_\beta }$
are compatible in
$p_{v_\beta }$
are compatible in
![]() $\mathbb {P}^*$
. Indeed, by (4),
$\mathbb {P}^*$
. Indeed, by (4),
![]() $\varphi ^{M_\alpha }(p_{u_\alpha })=^* p_w=^*\varphi ^{M_\beta }(p_{v_\beta })$
, and by (5),
$\varphi ^{M_\alpha }(p_{u_\alpha })=^* p_w=^*\varphi ^{M_\beta }(p_{v_\beta })$
, and by (5),
![]() $p_{u_\alpha }\in M_\beta $
. Thus, as
$p_{u_\alpha }\in M_\beta $
. Thus, as
![]() $p_{u_\alpha }\geq \varphi ^{M_\alpha }(p_{u_\alpha })\geq \varphi ^{M_\beta }(p_{v_\beta })$
, and as
$p_{u_\alpha }\geq \varphi ^{M_\alpha }(p_{u_\alpha })\geq \varphi ^{M_\beta }(p_{v_\beta })$
, and as
![]() $\varphi ^{M_\beta }$
is a residue function,
$\varphi ^{M_\beta }$
is a residue function,
![]() $p_{u_\alpha }$
is compatible with
$p_{u_\alpha }$
is compatible with
![]() $p_{v_\beta }$
.
$p_{v_\beta }$
.
Now, let
![]() $q\in \mathbb {P}^*$
be any common extension of
$q\in \mathbb {P}^*$
be any common extension of
![]() $p_{u_\alpha }$
and
$p_{u_\alpha }$
and
![]() $p_{v_\beta }$
. We will argue by induction on
$p_{v_\beta }$
. We will argue by induction on
![]() $\zeta \leq \rho $
that
$\zeta \leq \rho $
that
![]() $q\Vdash (\check {f}_{u_\alpha }\cup \check {f}_{v_\beta })\upharpoonright \zeta \in \dot {\mathbb {S}}_\zeta $
. Limit stages are immediate. For the successor stage, suppose that
$q\Vdash (\check {f}_{u_\alpha }\cup \check {f}_{v_\beta })\upharpoonright \zeta \in \dot {\mathbb {S}}_\zeta $
. Limit stages are immediate. For the successor stage, suppose that
![]() $\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_{u_\alpha })\cap \operatorname {dom}(f_{v_\beta })$
and that we have proved that
$\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_{u_\alpha })\cap \operatorname {dom}(f_{v_\beta })$
and that we have proved that
![]() $q\Vdash (\check {f}_{u_\alpha }\cup \check {f}_{v_\beta })\upharpoonright \zeta \in \dot {\mathbb {S}}_\zeta $
. Since
$q\Vdash (\check {f}_{u_\alpha }\cup \check {f}_{v_\beta })\upharpoonright \zeta \in \dot {\mathbb {S}}_\zeta $
. Since
![]() $f_{u_\alpha }\in M_\beta $
by (5),
$f_{u_\alpha }\in M_\beta $
by (5),
![]() $\langle \zeta ,\nu \rangle \in M_\beta $
. Thus,
$\langle \zeta ,\nu \rangle \in M_\beta $
. Thus,
![]() $\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_{v_\beta })\cap M_\beta =\operatorname {dom}(f_w)$
, since
$\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_{v_\beta })\cap M_\beta =\operatorname {dom}(f_w)$
, since
![]() $w=^*v_\beta \upharpoonright M_\beta $
. Since we also have that
$w=^*v_\beta \upharpoonright M_\beta $
. Since we also have that
![]() $w=^*u_\beta \upharpoonright M_\beta $
, it follows that
$w=^*u_\beta \upharpoonright M_\beta $
, it follows that
![]() $\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_{u_\beta })$
. Thus,
$\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_{u_\beta })$
. Thus,
![]() $\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_{u_\beta })\cap \operatorname {dom}(f_{v_\beta })\cap M_\beta =\operatorname {dom}(f_{u_\alpha })\cap \operatorname {dom}(f_{v_\alpha })\cap M_\alpha $
, with equality holding by (3) and the definition of a splitting function. Moreover,
$\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_{u_\beta })\cap \operatorname {dom}(f_{v_\beta })\cap M_\beta =\operatorname {dom}(f_{u_\alpha })\cap \operatorname {dom}(f_{v_\alpha })\cap M_\alpha $
, with equality holding by (3) and the definition of a splitting function. Moreover,
![]() $\zeta \in M_\alpha $
since
$\zeta \in M_\alpha $
since
![]() $\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_w)\subseteq M_\alpha $
.
$\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_w)\subseteq M_\alpha $
.
Now, pick a pair of distinct nodes
![]() $\langle \theta ,\tau \rangle \in f_{u_\alpha }(\zeta ,\nu )\times f_{v_\beta }(\zeta ,\nu )$
, and we will show that
$\langle \theta ,\tau \rangle \in f_{u_\alpha }(\zeta ,\nu )\times f_{v_\beta }(\zeta ,\nu )$
, and we will show that
![]() $(q,(f_{u_\alpha }\cup f_{v_\beta })\upharpoonright \zeta )$
forces in
$(q,(f_{u_\alpha }\cup f_{v_\beta })\upharpoonright \zeta )$
forces in
![]() $\mathbb {R}_\zeta $
that
$\mathbb {R}_\zeta $
that
![]() $\theta $
and
$\theta $
and
![]() $\tau $
are
$\tau $
are
![]() $\dot {T}_\zeta $
-incompatible. If
$\dot {T}_\zeta $
-incompatible. If
![]() $\theta $
is below level
$\theta $
is below level
![]() $\alpha $
, then
$\alpha $
, then
![]() $\theta \in (f_{u_\alpha }\upharpoonright M_\alpha )(\zeta ,\nu )=f_w(\zeta ,\nu )\subseteq f_{v_\beta }(\zeta ,\nu )$
. Thus,
$\theta \in (f_{u_\alpha }\upharpoonright M_\alpha )(\zeta ,\nu )=f_w(\zeta ,\nu )\subseteq f_{v_\beta }(\zeta ,\nu )$
. Thus,
![]() $(q,f_{v_\beta }\upharpoonright \zeta )\Vdash \theta ,\tau $
are
$(q,f_{v_\beta }\upharpoonright \zeta )\Vdash \theta ,\tau $
are
![]() $\dot {T}_\zeta $
-incompatible, and so
$\dot {T}_\zeta $
-incompatible, and so
![]() $(q,(f_{u_\alpha }\cup f_{v_\beta })\upharpoonright \zeta )$
forces this too. A similar argument applies if
$(q,(f_{u_\alpha }\cup f_{v_\beta })\upharpoonright \zeta )$
forces this too. A similar argument applies if
![]() $\tau $
is below level
$\tau $
is below level
![]() $\beta $
.
$\beta $
.
We therefore assume that
![]() $\theta $
is at or above level
$\theta $
is at or above level
![]() $\alpha $
and
$\alpha $
and
![]() $\tau $
is at or above level
$\tau $
is at or above level
![]() $\beta $
. Let m and n be chosen so that
$\beta $
. Let m and n be chosen so that
![]() $\theta $
is the mth node in
$\theta $
is the mth node in
![]() $f_{u_\alpha }(\zeta ,\nu )\backslash (\alpha \times \omega _1)$
and
$f_{u_\alpha }(\zeta ,\nu )\backslash (\alpha \times \omega _1)$
and
![]() $\tau $
is the nth node in
$\tau $
is the nth node in
![]() $f_{v_\beta }(\zeta ,\nu )\backslash (\beta \times \omega _1)$
. By assumption (3), letting
$f_{v_\beta }(\zeta ,\nu )\backslash (\beta \times \omega _1)$
. By assumption (3), letting
![]() $\Sigma :=\Sigma _\alpha =\Sigma _\beta $
, we know that
$\Sigma :=\Sigma _\alpha =\Sigma _\beta $
, we know that
![]() $\Sigma (\zeta ,\nu ,m,n)(L)$
and
$\Sigma (\zeta ,\nu ,m,n)(L)$
and
![]() $\Sigma (\zeta ,\nu ,m,n)(R)$
are two distinct nodes on the same level and also that
$\Sigma (\zeta ,\nu ,m,n)(R)$
are two distinct nodes on the same level and also that
and
Therefore,
![]() $(q,(f_{u_\alpha }\cup f_{v_\beta })\upharpoonright \zeta )$
forces that
$(q,(f_{u_\alpha }\cup f_{v_\beta })\upharpoonright \zeta )$
forces that
![]() $\tau $
and
$\tau $
and
![]() $\theta $
are incompatible in
$\theta $
are incompatible in
![]() $\dot {T}_\zeta $
, as we intended to show.▪
$\dot {T}_\zeta $
, as we intended to show.▪
The following item shows how we can obtain the desired splitting pairs of conditions.
Lemma 3.9 Suppose that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
and that
$\rho $
and that
![]() $\operatorname {dom}(\vec {M})$
satisfies the conclusion of Lemma 3.7. Fix
$\operatorname {dom}(\vec {M})$
satisfies the conclusion of Lemma 3.7. Fix
![]() $\alpha \in \operatorname {dom}(\vec {M})$
, and suppose that
$\alpha \in \operatorname {dom}(\vec {M})$
, and suppose that
![]() $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
is a residue pair for
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
is a residue pair for
![]() $(M_\alpha ,\mathbb {P}^*)$
. Finally, fix
$(M_\alpha ,\mathbb {P}^*)$
. Finally, fix
![]() $u,v,w$
so that
$u,v,w$
so that
![]() $\#^\rho _{\varphi ^{M_\alpha }}(u,v,w)$
. Then there exist extensions
$\#^\rho _{\varphi ^{M_\alpha }}(u,v,w)$
. Then there exist extensions
![]() $u^*\geq u$
and
$u^*\geq u$
and
![]() $v^*\geq v$
so that
$v^*\geq v$
so that
![]() $u^*,v^*$
are a splitting pair for
$u^*,v^*$
are a splitting pair for
![]() $(\varphi ^{M_\alpha },\rho )$
.
$(\varphi ^{M_\alpha },\rho )$
.
Proof Fix
![]() $u,v,w$
as in the statement of the lemma. We define a coordinatewise increasing sequence of triples
$u,v,w$
as in the statement of the lemma. We define a coordinatewise increasing sequence of triples
![]() $\langle \langle u_n,v_n,w_n\rangle :n\in \omega \rangle $
of conditions and a sequence
$\langle \langle u_n,v_n,w_n\rangle :n\in \omega \rangle $
of conditions and a sequence
![]() $\langle \langle \zeta _n,\nu _n,\theta _n,\tau _n\rangle :n\in \omega \rangle $
of tuples of ordinals and tree nodes so that
$\langle \langle \zeta _n,\nu _n,\theta _n,\tau _n\rangle :n\in \omega \rangle $
of tuples of ordinals and tree nodes so that
![]() $\langle u_0,v_0,w_0\rangle =\langle u,v,w\rangle $
and so that for each n,
$\langle u_0,v_0,w_0\rangle =\langle u,v,w\rangle $
and so that for each n,
-
•
 $\#^\rho _{\varphi ^{M_\alpha }}(u_n,v_n,w_n)$
holds;
$\#^\rho _{\varphi ^{M_\alpha }}(u_n,v_n,w_n)$
holds; -
•
 $\langle \zeta _n,\nu _n\rangle \in \operatorname {dom}(f_{u_n})\cap \operatorname {dom}(f_{v_n})\cap M_\alpha $
and
$\langle \zeta _n,\nu _n\rangle \in \operatorname {dom}(f_{u_n})\cap \operatorname {dom}(f_{v_n})\cap M_\alpha $
and
 $\langle \theta _n,\tau _n\rangle \in (f_{u_n}(\zeta _n,\nu _n)\backslash (\alpha \times \omega _1))\times (f_{v_n}(\zeta _n,\nu _n)\backslash (\alpha \times \omega _1))$
; and
$\langle \theta _n,\tau _n\rangle \in (f_{u_n}(\zeta _n,\nu _n)\backslash (\alpha \times \omega _1))\times (f_{v_n}(\zeta _n,\nu _n)\backslash (\alpha \times \omega _1))$
; and -
•
 $u_{n+1}$
and
$u_{n+1}$
and
 $v_{n+1}$
split
$v_{n+1}$
split
 $\langle \theta _n,\tau _n\rangle $
below
$\langle \theta _n,\tau _n\rangle $
below
 $\alpha $
.
$\alpha $
.
This is done with respect to some bookkeeping device in such a way that if
![]() $u^*$
is a sup of
$u^*$
is a sup of
![]() $\langle u_n:n\in \omega \rangle $
(and similarly for
$\langle u_n:n\in \omega \rangle $
(and similarly for
![]() $v^*$
), then for each
$v^*$
), then for each
![]() $\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_{u^*})\cap \operatorname {dom}(f_{v^*})\cap M_\alpha $
and each
$\langle \zeta ,\nu \rangle \in \operatorname {dom}(f_{u^*})\cap \operatorname {dom}(f_{v^*})\cap M_\alpha $
and each
![]() $\langle \theta ,\tau \rangle \in (f_{u^*}(\zeta ,\nu )\backslash (\alpha \times \omega _1))\times (f_{v^*}(\zeta ,\nu )\backslash (\alpha \times \omega _1))$
,
$\langle \theta ,\tau \rangle \in (f_{u^*}(\zeta ,\nu )\backslash (\alpha \times \omega _1))\times (f_{v^*}(\zeta ,\nu )\backslash (\alpha \times \omega _1))$
,
![]() $\langle \zeta ,\nu ,\theta ,\tau \rangle $
appears as the nth tuple for some n.
$\langle \zeta ,\nu ,\theta ,\tau \rangle $
appears as the nth tuple for some n.
To show the successor step, suppose that
![]() $u_n,v_n$
, and
$u_n,v_n$
, and
![]() $w_n$
are given, and consider
$w_n$
are given, and consider
![]() $\langle \zeta _n,\nu _n,\theta _n,\tau _n\rangle $
. Note that
$\langle \zeta _n,\nu _n,\theta _n,\tau _n\rangle $
. Note that
![]() $\#^{\zeta _n}_{\varphi ^{M_\alpha }}(u_n\upharpoonright \zeta _n,v_n\upharpoonright \zeta _n,w_n\upharpoonright \zeta _n)$
also holds. Then Lemma 3.5 applies since
$\#^{\zeta _n}_{\varphi ^{M_\alpha }}(u_n\upharpoonright \zeta _n,v_n\upharpoonright \zeta _n,w_n\upharpoonright \zeta _n)$
also holds. Then Lemma 3.5 applies since
![]() $\zeta _n\in M_\alpha $
and since
$\zeta _n\in M_\alpha $
and since
![]() $\mathbb {R}_\eta $
satisfies the dual residue property at
$\mathbb {R}_\eta $
satisfies the dual residue property at
![]() $M_\alpha $
for all
$M_\alpha $
for all
![]() $\eta \in M_\alpha \cap \rho $
. Thus, we may find conditions
$\eta \in M_\alpha \cap \rho $
. Thus, we may find conditions
![]() $u^{\prime }_n\geq u_n\upharpoonright \zeta _n$
,
$u^{\prime }_n\geq u_n\upharpoonright \zeta _n$
,
![]() $v^{\prime }_n\geq v_n\upharpoonright \zeta _n$
, and
$v^{\prime }_n\geq v_n\upharpoonright \zeta _n$
, and
![]() $w^{\prime }_n\geq w_n\upharpoonright \zeta _n$
so that
$w^{\prime }_n\geq w_n\upharpoonright \zeta _n$
so that
![]() $\#^{\zeta _n}_{\varphi ^{M_\alpha }}(u^{\prime }_n,v^{\prime }_n,w^{\prime }_n)$
and so that
$\#^{\zeta _n}_{\varphi ^{M_\alpha }}(u^{\prime }_n,v^{\prime }_n,w^{\prime }_n)$
and so that
![]() $u^{\prime }_n$
and
$u^{\prime }_n$
and
![]() $v^{\prime }_n$
split
$v^{\prime }_n$
split
![]() $\langle \theta _n,\tau _n\rangle $
below
$\langle \theta _n,\tau _n\rangle $
below
![]() $\alpha $
. Now, define
$\alpha $
. Now, define
![]() $f_{u_{n+1}}$
to be the function which equals
$f_{u_{n+1}}$
to be the function which equals
![]() $f_{u^{\prime }_n}$
on
$f_{u^{\prime }_n}$
on
![]() $\zeta _n$
and which equals
$\zeta _n$
and which equals
![]() $f_{u_n}$
on
$f_{u_n}$
on
![]() $[\zeta _n,\rho )$
. Moreover, let
$[\zeta _n,\rho )$
. Moreover, let
![]() $u_{n+1}$
be the pair
$u_{n+1}$
be the pair
![]() $(p_{u^{\prime }_{n}},f_{u_{n+1}})$
. Let
$(p_{u^{\prime }_{n}},f_{u_{n+1}})$
. Let
![]() $v_{n+1}$
and
$v_{n+1}$
and
![]() $w_{n+1}$
be defined similarly. Then
$w_{n+1}$
be defined similarly. Then
![]() $\#^\rho _{\varphi ^{M_\alpha }}(u_{n+1},v_{n+1},w_{n+1})$
holds, and
$\#^\rho _{\varphi ^{M_\alpha }}(u_{n+1},v_{n+1},w_{n+1})$
holds, and
![]() $u_{n+1}$
and
$u_{n+1}$
and
![]() $v_{n+1}$
split
$v_{n+1}$
split
![]() $\langle \theta _n,\tau _n\rangle $
below
$\langle \theta _n,\tau _n\rangle $
below
![]() $\alpha $
.
$\alpha $
.
This completes the construction of the sequence. Fix sups
![]() $u^*,v^*,w^*$
. Since
$u^*,v^*,w^*$
. Since
![]() $\#^\rho _{\varphi ^{M_\alpha }}(u_n,v_n,w_n)$
holds for all n,
$\#^\rho _{\varphi ^{M_\alpha }}(u_n,v_n,w_n)$
holds for all n,
![]() $\#^\rho _{\varphi ^{M_\alpha }}(u^*,v^*,w^*)$
also holds. By the choice of bookkeeping,
$\#^\rho _{\varphi ^{M_\alpha }}(u^*,v^*,w^*)$
also holds. By the choice of bookkeeping,
![]() $u^*,v^*$
is a splitting pair for
$u^*,v^*$
is a splitting pair for
![]() $(\varphi ^{M_\alpha },\rho )$
, completing the proof.▪
$(\varphi ^{M_\alpha },\rho )$
, completing the proof.▪
Lemma 3.10 Suppose that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
. Suppose that for each
$\rho $
. Suppose that for each
![]() $\alpha \in \operatorname {dom}(\vec {M})$
, there exist
$\alpha \in \operatorname {dom}(\vec {M})$
, there exist
![]() $u_\alpha ,v_\alpha $
which are a splitting pair for
$u_\alpha ,v_\alpha $
which are a splitting pair for
![]() $(\varphi ^{M_\alpha },\rho )$
, where
$(\varphi ^{M_\alpha },\rho )$
, where
![]() $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
is a residue pair for
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
is a residue pair for
![]() $(M_\alpha ,\mathbb {P}^*)$
. Then there exists
$(M_\alpha ,\mathbb {P}^*)$
. Then there exists
![]() $B\subseteq \operatorname {dom}(\vec {M})$
in
$B\subseteq \operatorname {dom}(\vec {M})$
in
![]() $\mathcal {F}^+$
so that for any
$\mathcal {F}^+$
so that for any
![]() $\alpha <\beta $
in B,
$\alpha <\beta $
in B,
![]() $u_\alpha ,v_\alpha \in M_\beta $
,
$u_\alpha ,v_\alpha \in M_\beta $
,
![]() $u_\alpha \upharpoonright M_\alpha =^*v_\beta \upharpoonright M_\beta $
, and
$u_\alpha \upharpoonright M_\alpha =^*v_\beta \upharpoonright M_\beta $
, and
![]() $u_\alpha $
is compatible with
$u_\alpha $
is compatible with
![]() $v_\beta $
.
$v_\beta $
.
Proof Suppose that for each
![]() $\alpha \in \operatorname {dom}(\vec {M})$
, we have a splitting pair
$\alpha \in \operatorname {dom}(\vec {M})$
, we have a splitting pair
![]() $u_\alpha ,v_\alpha $
for
$u_\alpha ,v_\alpha $
for
![]() $(\varphi ^{M_\alpha },\rho )$
; we also let
$(\varphi ^{M_\alpha },\rho )$
; we also let
![]() $w_\alpha \in \mathbb {R}_\rho \cap M_\alpha $
be a condition witnessing
$w_\alpha \in \mathbb {R}_\rho \cap M_\alpha $
be a condition witnessing
![]() $\#^\rho _{\varphi ^{M_\alpha }}(u_\alpha ,v_\alpha ,w_\alpha )$
. Let
$\#^\rho _{\varphi ^{M_\alpha }}(u_\alpha ,v_\alpha ,w_\alpha )$
. Let
![]() $\Sigma _\alpha $
be a splitting function for
$\Sigma _\alpha $
be a splitting function for
![]() $(u_\alpha ,v_\alpha )$
with respect to
$(u_\alpha ,v_\alpha )$
with respect to
![]() $M_\alpha $
, as in Definition 3.9. By Remark 3.6,
$M_\alpha $
, as in Definition 3.9. By Remark 3.6,
![]() $\Sigma _\alpha \in M_\alpha $
. Now, the function on
$\Sigma _\alpha \in M_\alpha $
. Now, the function on
![]() $\operatorname {dom}(\vec {M})$
defined by
$\operatorname {dom}(\vec {M})$
defined by
![]() $\alpha \mapsto \langle w_\alpha ,\Sigma _\alpha \rangle $
is regressive (since the pair can be coded by an ordinal below
$\alpha \mapsto \langle w_\alpha ,\Sigma _\alpha \rangle $
is regressive (since the pair can be coded by an ordinal below
![]() $\alpha $
). Since
$\alpha $
). Since
![]() $\operatorname {dom}(\vec {M})\in {\mathcal {F}^+}$
and
$\operatorname {dom}(\vec {M})\in {\mathcal {F}^+}$
and
![]() ${\mathcal {F}}$
is normal, there exists some
${\mathcal {F}}$
is normal, there exists some
![]() ${B}\subseteq \operatorname {dom}(\vec {M})$
which is also in
${B}\subseteq \operatorname {dom}(\vec {M})$
which is also in
![]() ${\mathcal {F}^+}$
on which that function takes a constant value, say
${\mathcal {F}^+}$
on which that function takes a constant value, say
![]() $\langle \bar {w},\Sigma \rangle $
. Moreover, by intersecting with a club and relabeling if necessary, we may assume that if
$\langle \bar {w},\Sigma \rangle $
. Moreover, by intersecting with a club and relabeling if necessary, we may assume that if
![]() $\alpha <\beta $
are in
$\alpha <\beta $
are in
![]() ${B}$
, then
${B}$
, then
![]() $u_\alpha ,v_\alpha \in M_\beta $
. But then, for any
$u_\alpha ,v_\alpha \in M_\beta $
. But then, for any
![]() $\alpha <\beta $
in B, we have that
$\alpha <\beta $
in B, we have that
![]() $u_\alpha \upharpoonright M_\alpha =^*\bar {w}=^*v_\beta \upharpoonright M_\beta $
. Therefore, for all
$u_\alpha \upharpoonright M_\alpha =^*\bar {w}=^*v_\beta \upharpoonright M_\beta $
. Therefore, for all
![]() $\alpha <\beta $
in
$\alpha <\beta $
in
![]() ${B}$
, the assumptions of Lemma 3.8 are satisfied, and consequently
${B}$
, the assumptions of Lemma 3.8 are satisfied, and consequently
![]() $u_\alpha $
and
$u_\alpha $
and
![]() $v_\beta $
are compatible.▪
$v_\beta $
are compatible.▪
Proposition 3.11
![]() $\mathbb {P}^*\Vdash \dot {\mathbb {S}}_\rho $
is
$\mathbb {P}^*\Vdash \dot {\mathbb {S}}_\rho $
is
![]() $\kappa $
-c.c.
$\kappa $
-c.c.
Proof Let
![]() $p\in \mathbb {P}^*$
be a condition, and suppose that
$p\in \mathbb {P}^*$
be a condition, and suppose that
![]() $p\Vdash \langle \dot {f}_\gamma :\gamma <\kappa \rangle $
is a sequence of conditions in
$p\Vdash \langle \dot {f}_\gamma :\gamma <\kappa \rangle $
is a sequence of conditions in
![]() $\dot {\mathbb {S}}_\rho $
. We will find some extension
$\dot {\mathbb {S}}_\rho $
. We will find some extension
![]() $p^*$
of p which forces that this sequence does not enumerate an antichain.
$p^*$
of p which forces that this sequence does not enumerate an antichain.
Let
![]() $\vec {M}$
be a sequence which is suitable with respect to the three parameters
$\vec {M}$
be a sequence which is suitable with respect to the three parameters
![]() $\mathbb {R}_\rho $
, p, and
$\mathbb {R}_\rho $
, p, and
![]() $\langle \dot {f}_\gamma :\gamma <\kappa \rangle $
, and which is in pre-splitting configuration up to
$\langle \dot {f}_\gamma :\gamma <\kappa \rangle $
, and which is in pre-splitting configuration up to
![]() $\rho $
. By removing an
$\rho $
. By removing an
![]() $\mathcal {I}$
-null set, we may assume that
$\mathcal {I}$
-null set, we may assume that
![]() $\operatorname {dom}(\vec {M})$
satisfies the conclusion of Lemma 3.7.
$\operatorname {dom}(\vec {M})$
satisfies the conclusion of Lemma 3.7.
Let
![]() $B:=\operatorname {dom}(\vec {M})$
. Since
$B:=\operatorname {dom}(\vec {M})$
. Since
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
, let
$\rho $
, let
![]() $\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in B\rangle $
be a residue system. For each
$\langle \langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle :\alpha \in B\rangle $
be a residue system. For each
![]() $\alpha \in B$
,
$\alpha \in B$
,
![]() $p\in \mathbb {P}^*\cap M_\alpha $
, and therefore we may find some extension
$p\in \mathbb {P}^*\cap M_\alpha $
, and therefore we may find some extension
![]() $p_\alpha $
of p so that
$p_\alpha $
of p so that
![]() $p_\alpha \in \operatorname {dom}(\varphi ^{M_\alpha })$
. We may also assume that for some function
$p_\alpha \in \operatorname {dom}(\varphi ^{M_\alpha })$
. We may also assume that for some function
![]() $f_\alpha $
in V,
$f_\alpha $
in V,
![]() $p_\alpha \Vdash _{\mathbb {P}^*}\dot {f}_\alpha =\check {f}_\alpha $
. Now, extend
$p_\alpha \Vdash _{\mathbb {P}^*}\dot {f}_\alpha =\check {f}_\alpha $
. Now, extend
![]() $\langle p_\alpha ,f_\alpha \rangle $
to a condition
$\langle p_\alpha ,f_\alpha \rangle $
to a condition
![]() $u_\alpha $
in
$u_\alpha $
in
![]() $D(\varphi ^{M_\alpha },\rho )$
. By Lemma 3.9, we may further extend
$D(\varphi ^{M_\alpha },\rho )$
. By Lemma 3.9, we may further extend
![]() $u_\alpha $
to a splitting pair
$u_\alpha $
to a splitting pair
![]() $\langle u^*_\alpha ,v^*_\alpha \rangle $
for
$\langle u^*_\alpha ,v^*_\alpha \rangle $
for
![]() $(\varphi ^{M_\alpha },\rho )$
. By Lemma 3.10, we may find some
$(\varphi ^{M_\alpha },\rho )$
. By Lemma 3.10, we may find some
![]() $B^*\subseteq B$
with
$B^*\subseteq B$
with
![]() $B^*\in {\mathcal {F}^+}$
so that for all
$B^*\in {\mathcal {F}^+}$
so that for all
![]() $\alpha <\beta $
in
$\alpha <\beta $
in
![]() $B^{*}$
,
$B^{*}$
,
![]() $u^*_\alpha $
and
$u^*_\alpha $
and
![]() $v^*_\beta $
are compatible. Let w be a condition extending them both. Then
$v^*_\beta $
are compatible. Let w be a condition extending them both. Then
![]() $p_w$
forces that
$p_w$
forces that
![]() $\check {f}_w$
extends both
$\check {f}_w$
extends both
![]() $\check {f}_{u^*_\alpha }$
and
$\check {f}_{u^*_\alpha }$
and
![]() $\check {f}_{v^*_\beta }$
and hence extends
$\check {f}_{v^*_\beta }$
and hence extends
![]() $\dot {f}_\alpha $
and
$\dot {f}_\alpha $
and
![]() $\dot {f}_\beta $
. Therefore,
$\dot {f}_\beta $
. Therefore,
![]() $p_w$
forces that
$p_w$
forces that
![]() $\dot {f}_\alpha $
and
$\dot {f}_\alpha $
and
![]() $\dot {f}_\beta $
are compatible in
$\dot {f}_\beta $
are compatible in
![]() $\dot {\mathbb {S}}_\rho $
.▪
$\dot {\mathbb {S}}_\rho $
.▪
We are now ready to verify that the second induction hypothesis holds at
![]() $\rho $
. We again remark that this proposition (and the later results which build off of it) is the only place in our work where we need the ineffability of
$\rho $
. We again remark that this proposition (and the later results which build off of it) is the only place in our work where we need the ineffability of
![]() $\kappa $
. In all other cases, the weak compactness of
$\kappa $
. In all other cases, the weak compactness of
![]() $\kappa $
suffices.
$\kappa $
suffices.
Proposition 3.12 Suppose that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
. Then there is an
$\rho $
. Then there is an
![]() $A\in \mathcal {I}$
so that for all
$A\in \mathcal {I}$
so that for all
![]() $\alpha \in \operatorname {dom}(\vec {M})\backslash A$
,
$\alpha \in \operatorname {dom}(\vec {M})\backslash A$
,
![]() $\mathbb {R}_\rho $
satisfies the dual residue property at
$\mathbb {R}_\rho $
satisfies the dual residue property at
![]() $M_\alpha $
.
$M_\alpha $
.
Proof We only deal with the case when
![]() $\mathbb {P}^*$
is not just the collapse poset
$\mathbb {P}^*$
is not just the collapse poset
![]() $\mathbb {P}$
(and hence we are in the case where
$\mathbb {P}$
(and hence we are in the case where
![]() $\kappa $
is ineffable, and
$\kappa $
is ineffable, and
![]() $\mathcal {F}=\mathcal {F}_{in}$
). The case when
$\mathcal {F}=\mathcal {F}_{in}$
). The case when
![]() $\mathbb {P}^*$
is the collapse
$\mathbb {P}^*$
is the collapse
![]() $\mathbb {P}$
is simpler and taken care of in [Reference Laver and Shelah30].
$\mathbb {P}$
is simpler and taken care of in [Reference Laver and Shelah30].
Suppose otherwise, for a contradiction. Then
is in
![]() ${\mathcal {F}^+}$
. Moreover, by removing an
${\mathcal {F}^+}$
. Moreover, by removing an
![]() $\mathcal {I}$
-null set if necessary, we may assume that B satisfies the conclusion of Lemma 3.7. We will derive our contradiction by creating a
$\mathcal {I}$
-null set if necessary, we may assume that B satisfies the conclusion of Lemma 3.7. We will derive our contradiction by creating a
![]() $\kappa $
-sized antichain in
$\kappa $
-sized antichain in
![]() $\mathbb {R}_\rho $
for which we can amalgamate many of the
$\mathbb {R}_\rho $
for which we can amalgamate many of the
![]() $\mathbb {P}^*$
-parts. This will then lead to a
$\mathbb {P}^*$
-parts. This will then lead to a
![]() $\kappa $
-sized antichain in
$\kappa $
-sized antichain in
![]() $\mathbb {S}_\rho $
in some V-generic extension over
$\mathbb {S}_\rho $
in some V-generic extension over
![]() $\mathbb {P}^*$
.
$\mathbb {P}^*$
.
For each
![]() $\alpha \in B$
, we fix a residue pair
$\alpha \in B$
, we fix a residue pair
![]() $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
![]() $(M_\alpha ,\mathbb {P}^*)$
and a triple
$(M_\alpha ,\mathbb {P}^*)$
and a triple
![]() $\langle u_\alpha ,v_\alpha ,w_\alpha \rangle $
which witnesses that
$\langle u_\alpha ,v_\alpha ,w_\alpha \rangle $
which witnesses that
![]() $\mathbb {R}_\rho $
does not satisfy the dual residue property at
$\mathbb {R}_\rho $
does not satisfy the dual residue property at
![]() $M_\alpha $
. Thus,
$M_\alpha $
. Thus,
![]() $\#^\rho _{\varphi ^{M_\alpha }}(u_\alpha ,v_\alpha ,w_\alpha )$
holds, but for any
$\#^\rho _{\varphi ^{M_\alpha }}(u_\alpha ,v_\alpha ,w_\alpha )$
holds, but for any
![]() $w^*\geq _{\mathbb {R}_\rho \cap M_\alpha }w_\alpha $
, either
$w^*\geq _{\mathbb {R}_\rho \cap M_\alpha }w_\alpha $
, either
![]() $w^*$
is not a residue for
$w^*$
is not a residue for
![]() $u_\alpha $
to
$u_\alpha $
to
![]() $M_\alpha $
or
$M_\alpha $
or
![]() $w^*$
is not a residue for
$w^*$
is not a residue for
![]() $v_\alpha $
to
$v_\alpha $
to
![]() $M_\alpha $
. In particular, for each such
$M_\alpha $
. In particular, for each such
![]() $w^*$
, we may find a further extension in
$w^*$
, we may find a further extension in
![]() $\mathbb {R}_\rho \cap M_\alpha $
which is either incompatible with
$\mathbb {R}_\rho \cap M_\alpha $
which is either incompatible with
![]() $u_\alpha $
or incompatible with
$u_\alpha $
or incompatible with
![]() $v_\alpha $
in
$v_\alpha $
in
![]() $\mathbb {R}_\rho $
.
$\mathbb {R}_\rho $
.
By Lemma 3.9, we may extend
![]() $\langle u_\alpha ,v_\alpha ,w_\alpha \rangle $
to another triple
$\langle u_\alpha ,v_\alpha ,w_\alpha \rangle $
to another triple
![]() $\langle u^*_\alpha ,v^*_\alpha ,w^*_\alpha \rangle $
so that
$\langle u^*_\alpha ,v^*_\alpha ,w^*_\alpha \rangle $
so that
![]() $u^*_\alpha $
and
$u^*_\alpha $
and
![]() $v^*_\alpha $
are a splitting pair for
$v^*_\alpha $
are a splitting pair for
![]() $M_\alpha $
. By Lemma 3.10, we may find some
$M_\alpha $
. By Lemma 3.10, we may find some
![]() $B^*\subseteq B$
with
$B^*\subseteq B$
with
![]() $B^*\in \mathcal {F}^+$
so that for all
$B^*\in \mathcal {F}^+$
so that for all
![]() $\alpha ,\beta \in B^*$
with
$\alpha ,\beta \in B^*$
with
![]() $\alpha <\beta $
,
$\alpha <\beta $
,
![]() $w^*_\alpha =^*w^*_\beta $
,
$w^*_\alpha =^*w^*_\beta $
,
![]() $u^*_\alpha $
and
$u^*_\alpha $
and
![]() $v^*_\alpha $
are in
$v^*_\alpha $
are in
![]() $M_\beta $
, and
$M_\beta $
, and
![]() $u_\alpha ^*$
is compatible with
$u_\alpha ^*$
is compatible with
![]() $v_\beta ^*$
. We let
$v_\beta ^*$
. We let
![]() $\bar {w}^*$
denote a condition which is
$\bar {w}^*$
denote a condition which is
![]() $=^*$
equal to
$=^*$
equal to
![]() $w^*_\alpha $
for
$w^*_\alpha $
for
![]() $\alpha \in B^*$
.
$\alpha \in B^*$
.
Next, for each
![]() $\alpha <\beta $
both in
$\alpha <\beta $
both in
![]() $B^*$
, we define a condition
$B^*$
, we define a condition
![]() $w^*_{\alpha ,\beta }$
. Fix such
$w^*_{\alpha ,\beta }$
. Fix such
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Since
$\beta $
. Since
![]() $u^*_\alpha \in M_\beta $
is compatible with
$u^*_\alpha \in M_\beta $
is compatible with
![]() $v^*_\beta $
, there is an extension
$v^*_\beta $
, there is an extension
![]() $w^*_{\alpha ,\beta }$
of
$w^*_{\alpha ,\beta }$
of
![]() $u^*_\alpha $
in
$u^*_\alpha $
in
![]() $\mathbb {R}_\rho \cap M_\beta $
which is a residue for
$\mathbb {R}_\rho \cap M_\beta $
which is a residue for
![]() $v_\beta ^*$
to
$v_\beta ^*$
to
![]() $\mathbb {R}_\rho \cap M_\beta $
. Since
$\mathbb {R}_\rho \cap M_\beta $
. Since
![]() $\beta \in B$
and since
$\beta \in B$
and since
![]() $w^*_{\alpha ,\beta }$
is a residue for
$w^*_{\alpha ,\beta }$
is a residue for
![]() $v^*_\beta $
, we may further extend (and relabel if necessary) to assume that
$v^*_\beta $
, we may further extend (and relabel if necessary) to assume that
![]() $w^*_{\alpha ,\beta }$
is incompatible with
$w^*_{\alpha ,\beta }$
is incompatible with
![]() $u^*_\beta $
. Since
$u^*_\beta $
. Since
![]() $p_{w^*_{\alpha ,\beta }}\geq p_{u^*_\alpha }\geq p^*(M_\alpha )$
, we may further assume that
$p_{w^*_{\alpha ,\beta }}\geq p_{u^*_\alpha }\geq p^*(M_\alpha )$
, we may further assume that
![]() $p_{w^*_{\alpha ,\beta }}$
is in the domain of
$p_{w^*_{\alpha ,\beta }}$
is in the domain of
![]() $\varphi ^{M_\alpha }$
.
$\varphi ^{M_\alpha }$
.
We now set up an application of the ineffability of
![]() $\kappa $
. For each
$\kappa $
. For each
![]() $\beta \in B^*$
, we define the function
$\beta \in B^*$
, we define the function
![]() $E_\beta $
by
$E_\beta $
by
Formally, we ought to apply the ineffability of
![]() $\kappa $
to a sequence
$\kappa $
to a sequence
![]() $\vec {A}$
where the
$\vec {A}$
where the
![]() $\alpha $
th element on the sequence is a subset of
$\alpha $
th element on the sequence is a subset of
![]() $\alpha $
. However, we will work with the sets
$\alpha $
. However, we will work with the sets
![]() $E_\beta $
; this poses no loss of generality since, by using the
$E_\beta $
; this poses no loss of generality since, by using the
![]() $\lhd $
-least bijection from
$\lhd $
-least bijection from
![]() $\mathbb {R}_\rho $
onto
$\mathbb {R}_\rho $
onto
![]() $\kappa $
and the Gödel pairing function, we can code
$\kappa $
and the Gödel pairing function, we can code
![]() $E_\beta $
as a subset of
$E_\beta $
as a subset of
![]() $\beta $
.
$\beta $
.
Since
![]() $\kappa $
is ineffable and
$\kappa $
is ineffable and
![]() $B^*\in \mathcal {F}^+$
, we can find a subset E of
$B^*\in \mathcal {F}^+$
, we can find a subset E of
![]() $\kappa \times \mathbb {R}_\rho $
and a stationary
$\kappa \times \mathbb {R}_\rho $
and a stationary
![]() $S\subseteq B^*$
so that for all
$S\subseteq B^*$
so that for all
![]() $\beta \in S$
,
$\beta \in S$
,
![]() $E\cap (\beta \times (M_\beta \cap \mathbb {R}_\rho ))=E_\beta $
. We observe that E is a function: if
$E\cap (\beta \times (M_\beta \cap \mathbb {R}_\rho ))=E_\beta $
. We observe that E is a function: if
![]() $(\alpha ,w)$
and
$(\alpha ,w)$
and
![]() $(\alpha ,w')$
are both in E, fix some
$(\alpha ,w')$
are both in E, fix some
![]() $\beta \in S$
large enough so that
$\beta \in S$
large enough so that
![]() $w,w'\in M_\beta \cap \mathbb {R}_\rho $
. Then
$w,w'\in M_\beta \cap \mathbb {R}_\rho $
. Then
![]() $(\alpha ,w)$
and
$(\alpha ,w)$
and
![]() $(\alpha ,w')$
are in
$(\alpha ,w')$
are in
![]() $E\cap (\beta \times (M_\beta \cap \mathbb {R}_\rho ))=E_\beta $
. Since
$E\cap (\beta \times (M_\beta \cap \mathbb {R}_\rho ))=E_\beta $
. Since
![]() $E_\beta $
is a function,
$E_\beta $
is a function,
![]() $w=w'$
. We can now rephrase the coherence as follows: if
$w=w'$
. We can now rephrase the coherence as follows: if
![]() $\beta \in S$
, then
$\beta \in S$
, then
![]() $E\upharpoonright \beta =E_\beta $
, since
$E\upharpoonright \beta =E_\beta $
, since
![]() $E\upharpoonright \beta $
and
$E\upharpoonright \beta $
and
![]() $E_\beta $
are both functions with domain
$E_\beta $
are both functions with domain
![]() $B^*\cap \beta $
and
$B^*\cap \beta $
and
![]() $E_\beta \subseteq E\upharpoonright \beta $
.
$E_\beta \subseteq E\upharpoonright \beta $
.
Next,
![]() $B^*\subseteq \operatorname {dom}(E)$
. Indeed, for each
$B^*\subseteq \operatorname {dom}(E)$
. Indeed, for each
![]() $\beta \in S$
,
$\beta \in S$
,
![]() $E\upharpoonright \beta =E_\beta $
, and the domain of
$E\upharpoonright \beta =E_\beta $
, and the domain of
![]() $E_\beta $
is
$E_\beta $
is
![]() $B^*\cap \beta $
. Since S is unbounded (in fact stationary) in
$B^*\cap \beta $
. Since S is unbounded (in fact stationary) in
![]() $\kappa $
, there are unboundedly many
$\kappa $
, there are unboundedly many
![]() $\beta $
so that
$\beta $
so that
![]() $E\upharpoonright \beta =E_\beta $
, from which the conclusion follows. And finally, if
$E\upharpoonright \beta =E_\beta $
, from which the conclusion follows. And finally, if
![]() $\alpha \in B^*$
, then for any
$\alpha \in B^*$
, then for any
![]() $\beta \in S\backslash (\alpha +1)$
,
$\beta \in S\backslash (\alpha +1)$
,
![]() $E(\alpha )=w^*_{\alpha ,\beta }$
, since
$E(\alpha )=w^*_{\alpha ,\beta }$
, since
![]() $E(\alpha )=E_\beta (\alpha )=w^*_{\alpha ,\beta }$
.
$E(\alpha )=E_\beta (\alpha )=w^*_{\alpha ,\beta }$
.
Now, we press down residues for conditions indexed by S. Since
![]() $S\subseteq B^*=\operatorname {dom}(E)$
,
$S\subseteq B^*=\operatorname {dom}(E)$
,
![]() $E(\alpha )$
is defined for each
$E(\alpha )$
is defined for each
![]() $\alpha \in S$
. Moreover,
$\alpha \in S$
. Moreover,
![]() $p_{E(\alpha )}$
is in the domain of
$p_{E(\alpha )}$
is in the domain of
![]() $\varphi ^{M_\alpha }$
since it equals
$\varphi ^{M_\alpha }$
since it equals
![]() $w^*_{\alpha ,\beta }$
for some/any
$w^*_{\alpha ,\beta }$
for some/any
![]() $\beta \in S\backslash (\alpha +1)$
, and since
$\beta \in S\backslash (\alpha +1)$
, and since
![]() $w^*_{\alpha ,\beta }$
is in the domain of
$w^*_{\alpha ,\beta }$
is in the domain of
![]() $\varphi ^{M_\alpha }$
. Then
$\varphi ^{M_\alpha }$
. Then
![]() $\varphi ^{M_\alpha }(p_{E(\alpha )})$
is a condition in
$\varphi ^{M_\alpha }(p_{E(\alpha )})$
is a condition in
![]() $M_\alpha \cap \mathbb {R}_\rho $
, and each such condition can be coded by an element of
$M_\alpha \cap \mathbb {R}_\rho $
, and each such condition can be coded by an element of
![]() $\alpha $
, using the
$\alpha $
, using the
![]() $\lhd $
-least bijection from
$\lhd $
-least bijection from
![]() $\mathbb {R}_\rho $
onto
$\mathbb {R}_\rho $
onto
![]() $\kappa $
. Thus, the function
$\kappa $
. Thus, the function
![]() $\alpha \mapsto \varphi ^{M_\alpha }(p_{E(\alpha )})$
on S is regressive, and so we can find a stationary
$\alpha \mapsto \varphi ^{M_\alpha }(p_{E(\alpha )})$
on S is regressive, and so we can find a stationary
![]() $S^*\subseteq S$
so that it has a constant value, say the condition
$S^*\subseteq S$
so that it has a constant value, say the condition
![]() $p^{**}$
.
$p^{**}$
.
Now, fix
![]() $\alpha <\beta $
in
$\alpha <\beta $
in
![]() $S^*$
, and we will show that
$S^*$
, and we will show that
![]() $p_{E(\alpha )}$
and
$p_{E(\alpha )}$
and
![]() $p_{E(\beta )}$
are compatible in
$p_{E(\beta )}$
are compatible in
![]() $\mathbb {P}^*$
. Indeed,
$\mathbb {P}^*$
. Indeed,
![]() $E(\alpha )=w^*_{\alpha ,\beta }$
is an element of
$E(\alpha )=w^*_{\alpha ,\beta }$
is an element of
![]() $M_\beta \cap \mathbb {R}_\rho $
. In addition,
$M_\beta \cap \mathbb {R}_\rho $
. In addition,
![]() $p_{w^*_{\alpha ,\beta }}\geq \varphi ^{M_\alpha }(p_{w^*_{\alpha ,\beta }})=p^{**}=\varphi ^{M_\beta }(p_{E(\beta )})$
. Thus,
$p_{w^*_{\alpha ,\beta }}\geq \varphi ^{M_\alpha }(p_{w^*_{\alpha ,\beta }})=p^{**}=\varphi ^{M_\beta }(p_{E(\beta )})$
. Thus,
![]() $p_{E(\alpha )}=p_{w^*_{\alpha ,\beta }}$
extends, inside of
$p_{E(\alpha )}=p_{w^*_{\alpha ,\beta }}$
extends, inside of
![]() $M_\beta $
, the residue of
$M_\beta $
, the residue of
![]() $p_{E(\beta )}$
to
$p_{E(\beta )}$
to
![]() $M_\beta $
.
$M_\beta $
.
![]() $p_{E(\alpha )}$
and
$p_{E(\alpha )}$
and
![]() $p_{E(\beta )}$
are therefore compatible in
$p_{E(\beta )}$
are therefore compatible in
![]() $\mathbb {P}^*$
.
$\mathbb {P}^*$
.
However, for such
![]() $\alpha <\beta $
, we also know that
$\alpha <\beta $
, we also know that
![]() $E(\alpha )$
and
$E(\alpha )$
and
![]() $E(\beta )$
are incompatible conditions in
$E(\beta )$
are incompatible conditions in
![]() $\mathbb {R}_\rho $
, since
$\mathbb {R}_\rho $
, since
![]() $E(\beta )$
extends
$E(\beta )$
extends
![]() $u^*_\beta $
and since
$u^*_\beta $
and since
![]() $E(\alpha )=w^*_{\alpha ,\beta }$
is incompatible with
$E(\alpha )=w^*_{\alpha ,\beta }$
is incompatible with
![]() $u^*_\beta $
. Thus, if q is any condition which extends
$u^*_\beta $
. Thus, if q is any condition which extends
![]() $p_{E(\alpha )}$
and
$p_{E(\alpha )}$
and
![]() $p_{E(\beta )}$
in
$p_{E(\beta )}$
in
![]() $\mathbb {P}^*$
, then q must force that
$\mathbb {P}^*$
, then q must force that
![]() $f_{E(\alpha )}$
and
$f_{E(\alpha )}$
and
![]() $f_{E(\beta )}$
are incompatible conditions in
$f_{E(\beta )}$
are incompatible conditions in
![]() $\dot {\mathbb {S}}_\rho $
.
$\dot {\mathbb {S}}_\rho $
.
Now, we can create our
![]() $\kappa $
-sized antichain of specializing conditions. Let
$\kappa $
-sized antichain of specializing conditions. Let
![]() $G^*$
be a V-generic filter over
$G^*$
be a V-generic filter over
![]() $\mathbb {P}^*$
which contains the condition
$\mathbb {P}^*$
which contains the condition
![]() $p^{**}$
, and recall that
$p^{**}$
, and recall that
![]() $p^{**}=\varphi ^{M_\alpha }(p_{E(\alpha )})$
for all
$p^{**}=\varphi ^{M_\alpha }(p_{E(\alpha )})$
for all
![]() $\alpha \in S^*$
. By Lemma 2.13, the set
$\alpha \in S^*$
. By Lemma 2.13, the set
is unbounded in
![]() $\kappa $
. Therefore, if
$\kappa $
. Therefore, if
![]() $\alpha <\beta $
are in X, then
$\alpha <\beta $
are in X, then
![]() $f_{E(\alpha )}$
and
$f_{E(\alpha )}$
and
![]() $f_{E(\beta )}$
are incompatible conditions in
$f_{E(\beta )}$
are incompatible conditions in
![]() $\dot {\mathbb {S}}_\rho [G]$
. Since
$\dot {\mathbb {S}}_\rho [G]$
. Since
![]() $\kappa $
is a cardinal after forcing with
$\kappa $
is a cardinal after forcing with
![]() $\mathbb {P}^*$
and since X has size
$\mathbb {P}^*$
and since X has size
![]() $\kappa $
, this gives a
$\kappa $
, this gives a
![]() $\kappa $
-sized antichain in
$\kappa $
-sized antichain in
![]() $\dot {\mathbb {S}}_\rho [G]$
. This contradicts Proposition 3.11 and completes the proof.▪
$\dot {\mathbb {S}}_\rho [G]$
. This contradicts Proposition 3.11 and completes the proof.▪
Here, we comment on the use of the ineffability of
![]() $\kappa $
. In the original Laver–Shelah argument,
$\kappa $
. In the original Laver–Shelah argument,
![]() $\mathbb {P}^*$
is just the collapse forcing. Thus, their entire forcing is
$\mathbb {P}^*$
is just the collapse forcing. Thus, their entire forcing is
![]() $\kappa $
-c.c. However, in our setup,
$\kappa $
-c.c. However, in our setup,
![]() $\mathbb {P}^*$
will in general fail to be
$\mathbb {P}^*$
will in general fail to be
![]() $\kappa $
-c.c., and consequently it is not enough to find a
$\kappa $
-c.c., and consequently it is not enough to find a
![]() $\kappa $
-sized antichain in
$\kappa $
-sized antichain in
![]() $\mathbb {P}^*\ast \dot {\mathbb {S}}_\rho =\mathbb {R}_\rho $
. Rather, we need to arrange that there is a
$\mathbb {P}^*\ast \dot {\mathbb {S}}_\rho =\mathbb {R}_\rho $
. Rather, we need to arrange that there is a
![]() $\kappa $
-sized antichain in
$\kappa $
-sized antichain in
![]() $\mathbb {R}_\rho $
for which we can amalgamate plenty of the
$\mathbb {R}_\rho $
for which we can amalgamate plenty of the
![]() $\mathbb {P}^*$
-parts of the conditions. This in turn requires that we are able to press down on the residues of the
$\mathbb {P}^*$
-parts of the conditions. This in turn requires that we are able to press down on the residues of the
![]() $\mathbb {P}^*$
-parts. Considering the array
$\mathbb {P}^*$
-parts. Considering the array
![]() $\langle w^*_{\alpha ,\beta }:\alpha ,\beta \in B^*\wedge \alpha <\beta \rangle $
from the proof of the previous result, we need to find a stationary
$\langle w^*_{\alpha ,\beta }:\alpha ,\beta \in B^*\wedge \alpha <\beta \rangle $
from the proof of the previous result, we need to find a stationary
![]() $S\subseteq B^*$
on which, for each
$S\subseteq B^*$
on which, for each
![]() $\alpha \in S$
, the function on
$\alpha \in S$
, the function on
![]() $S\backslash (\alpha +1)$
taking
$S\backslash (\alpha +1)$
taking
![]() $\beta $
to
$\beta $
to
![]() $w^*_{\alpha ,\beta }$
is independent of
$w^*_{\alpha ,\beta }$
is independent of
![]() $\beta $
, say taking value
$\beta $
, say taking value
![]() $w^{**}_\alpha $
. Then, using the stationarity of S, we pressed down on the residue of
$w^{**}_\alpha $
. Then, using the stationarity of S, we pressed down on the residue of
![]() $w^{**}_\alpha $
. The ineffability of
$w^{**}_\alpha $
. The ineffability of
![]() $\kappa $
allowed us to create a function, namely E, out of the above array with
$\kappa $
allowed us to create a function, namely E, out of the above array with
![]() $\operatorname {dom}(E)$
containing a stationary set on which the approximations (the
$\operatorname {dom}(E)$
containing a stationary set on which the approximations (the
![]() $E_\beta $
) cohere. We were not able to create this function and set up an application of pressing down just assuming that
$E_\beta $
) cohere. We were not able to create this function and set up an application of pressing down just assuming that
![]() $\kappa $
is weakly compact.
$\kappa $
is weakly compact.
However, in the case that
![]() $\mathbb {P}^*$
is just the collapse, then a weakly compact cardinal suffices for the entirety of the argument, since the entire poset
$\mathbb {P}^*$
is just the collapse, then a weakly compact cardinal suffices for the entirety of the argument, since the entire poset
![]() $\mathbb {P}\ast \dot {\mathbb {S}}_\rho $
is then
$\mathbb {P}\ast \dot {\mathbb {S}}_\rho $
is then
![]() $\kappa $
-c.c. In this case, we only need to create an unbounded
$\kappa $
-c.c. In this case, we only need to create an unbounded
![]() $Z\subseteq B^*$
on which the function
$Z\subseteq B^*$
on which the function
![]() $\beta \mapsto w^*_{\alpha ,\beta }$
is independent of
$\beta \mapsto w^*_{\alpha ,\beta }$
is independent of
![]() $\beta $
, for each
$\beta $
, for each
![]() $\alpha \in Z$
and
$\alpha \in Z$
and
![]() $\beta \in Z\backslash (\alpha +1)$
; this is because
$\beta \in Z\backslash (\alpha +1)$
; this is because
![]() $\langle w^{**}_\alpha :\alpha \in Z\rangle $
would then be a
$\langle w^{**}_\alpha :\alpha \in Z\rangle $
would then be a
![]() $\kappa $
-sized antichain in
$\kappa $
-sized antichain in
![]() $\mathbb {P}\ast \dot {\mathbb {S}}_\rho $
, a contradiction. Z can be constructed by working inside a
$\mathbb {P}\ast \dot {\mathbb {S}}_\rho $
, a contradiction. Z can be constructed by working inside a
![]() $\kappa $
-model
$\kappa $
-model
![]() $M^*$
containing all of the relevant information, for which there exists an
$M^*$
containing all of the relevant information, for which there exists an
![]() $M^*$
-normal ultrafilter containing B as an element.
$M^*$
-normal ultrafilter containing B as an element.
We have now completed the proof of Theorem 3.1. We conclude with a corollary which adds to that theorem an additional clause about the dual residue property; this will be useful later.
Corollary 3.13 Suppose that
![]() $\mathbb {P}^*$
is
$\mathbb {P}^*$
is
![]() ${\mathcal {F}}$
-strongly proper and that
${\mathcal {F}}$
-strongly proper and that
![]() $\dot {\mathbb {S}}_{\kappa ^+}$
is a
$\dot {\mathbb {S}}_{\kappa ^+}$
is a
![]() $\mathbb {P}^*$
-name for a
$\mathbb {P}^*$
-name for a
![]() $\kappa ^+$
-length, countable support iteration specializing Aronszajn trees on
$\kappa ^+$
-length, countable support iteration specializing Aronszajn trees on
![]() $\kappa $
. Then, for all
$\kappa $
. Then, for all
![]() $\rho <\kappa ^+$
,
$\rho <\kappa ^+$
,
-
(1)
 $\mathbb {P}^*$
forces that
$\mathbb {P}^*$
forces that
 $\dot {\mathbb {S}}_\rho $
is
$\dot {\mathbb {S}}_\rho $
is
 $\kappa $
-c.c.; and
$\kappa $
-c.c.; and -
(2) if
 $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
 $\rho $
, then there is some
$\rho $
, then there is some
 $A\subseteq \operatorname {dom}(\vec {M})$
with
$A\subseteq \operatorname {dom}(\vec {M})$
with
 $A\in \mathcal {I}$
so that for all
$A\in \mathcal {I}$
so that for all
 $\alpha \in \operatorname {dom}(\vec {M})\backslash A$
,
$\alpha \in \operatorname {dom}(\vec {M})\backslash A$
,
 $\mathbb {R}_\rho $
satisfies the dual residue property at
$\mathbb {R}_\rho $
satisfies the dual residue property at
 $M_\alpha $
. Hence, for all
$M_\alpha $
. Hence, for all
 $\zeta \in M_\alpha \cap (\rho +1)$
,
$\zeta \in M_\alpha \cap (\rho +1)$
,
 $\mathbb {R}_\zeta $
satisfies the dual residue property at
$\mathbb {R}_\zeta $
satisfies the dual residue property at
 $M_\alpha $
.
$M_\alpha $
.
4
 ${\mathcal {F}}$
-strongly proper posets and preserving stationary sets
${\mathcal {F}}$
-strongly proper posets and preserving stationary sets
In this section, we will prove that the appropriate quotients preserve stationary sets of cofinality
![]() $\omega $
ordinals. We will apply this result in Section 6 when we show that our intended club-adding iteration is
$\omega $
ordinals. We will apply this result in Section 6 when we show that our intended club-adding iteration is
![]() ${\mathcal {F}}$
-completely proper (see Definition 5.3). In the first part of this section, we will prove some helpful lemmas which we use in the second part to complete proof of the preservation of the relevant stationary sets.
${\mathcal {F}}$
-completely proper (see Definition 5.3). In the first part of this section, we will prove some helpful lemmas which we use in the second part to complete proof of the preservation of the relevant stationary sets.
For the remainder of this section, we fix an
![]() ${\mathcal {F}}$
-strongly proper poset
${\mathcal {F}}$
-strongly proper poset
![]() $\mathbb {P}^*$
and an iteration
$\mathbb {P}^*$
and an iteration
![]() $\dot {\mathbb {S}}_\rho $
of length
$\dot {\mathbb {S}}_\rho $
of length
![]() $\rho <\kappa ^+$
specializing Aronszajn trees in the extension by
$\rho <\kappa ^+$
specializing Aronszajn trees in the extension by
![]() $\mathbb {P}^*$
(see the beginning of Section 3 for a more precise definition and relevant notation). Note that the conclusions of Corollary 3.13 hold.
$\mathbb {P}^*$
(see the beginning of Section 3 for a more precise definition and relevant notation). Note that the conclusions of Corollary 3.13 hold.
We first prove two lemmas which describe how the residue functions with respect to two models on a suitable sequence interact. More precisely, suppose we have a suitable sequence
![]() $\vec {M}$
, where
$\vec {M}$
, where
![]() $\alpha <\beta $
are both in
$\alpha <\beta $
are both in
![]() $\operatorname {dom}(\vec {M})$
and
$\operatorname {dom}(\vec {M})$
and
![]() $M_\alpha $
and
$M_\alpha $
and
![]() $M_\beta $
have respective residue pairs
$M_\beta $
have respective residue pairs
![]() $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
and
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
and
![]() $\langle p^*(M_\beta ),\varphi ^{M_\beta }\rangle $
with respect to
$\langle p^*(M_\beta ),\varphi ^{M_\beta }\rangle $
with respect to
![]() $\mathbb {P}^*$
. A natural question is whether, on a dense set,
$\mathbb {P}^*$
. A natural question is whether, on a dense set,
![]() $\varphi ^{M_\alpha }(\varphi ^{M_\beta }(q))=^*\varphi ^{M_\alpha }(q)$
, i.e., whether the
$\varphi ^{M_\alpha }(\varphi ^{M_\beta }(q))=^*\varphi ^{M_\alpha }(q)$
, i.e., whether the
![]() $M_\alpha $
-residue of the
$M_\alpha $
-residue of the
![]() $M_\beta $
-residue is equivalent to the
$M_\beta $
-residue is equivalent to the
![]() $M_\alpha $
-residue. Proposition 4.2 shows that this is the case.
$M_\alpha $
-residue. Proposition 4.2 shows that this is the case.
Lemma 4.1 Suppose that
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\mathbb {P}^*$
-suitable with residue system
$\mathbb {P}^*$
-suitable with residue system
and that
![]() $\alpha <\beta $
are in
$\alpha <\beta $
are in
![]() $\operatorname {dom}(\vec {M})$
.
$\operatorname {dom}(\vec {M})$
.
-
(1) For every
 $p\in \mathbb {P}^*$
that extends both
$p\in \mathbb {P}^*$
that extends both
 $p^*(M_\alpha )$
and
$p^*(M_\alpha )$
and
 $p^*(M_\beta )$
, there is an extension
$p^*(M_\beta )$
, there is an extension
 $p^*\geq _{\mathbb {P}^*}p$
with
$p^*\geq _{\mathbb {P}^*}p$
with
 $p^*\in \operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta })$
.
$p^*\in \operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta })$
. -
(2)
 $D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta }):=\left \{ q\in \operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta }):\varphi ^{M_\beta }(q)\in \operatorname {dom}(\varphi ^{M_\alpha })\right \}$
is
$D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta }):=\left \{ q\in \operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta }):\varphi ^{M_\beta }(q)\in \operatorname {dom}(\varphi ^{M_\alpha })\right \}$
is
 $={}^*$
-countably closed and dense in
$={}^*$
-countably closed and dense in
 $\mathbb {P}^*/\left \{ p^*(M_\alpha ),p^*(M_\beta ) \right \}$
.Footnote
5
$\mathbb {P}^*/\left \{ p^*(M_\alpha ),p^*(M_\beta ) \right \}$
.Footnote
5
Proof For (1), we apply a dovetailing construction using the properties of the residue functions. Define, by recursion, an increasing sequence
![]() $\langle p_n:n\in \omega \rangle $
of extensions of p so that
$\langle p_n:n\in \omega \rangle $
of extensions of p so that
![]() $p_{2n+1}\in \operatorname {dom}(\varphi ^{M_\alpha })$
and, for
$p_{2n+1}\in \operatorname {dom}(\varphi ^{M_\alpha })$
and, for
![]() $n>0$
,
$n>0$
,
![]() $p_{2n}\in \operatorname {dom}(\varphi ^{M_\beta })$
. Let
$p_{2n}\in \operatorname {dom}(\varphi ^{M_\beta })$
. Let
![]() $p^*$
be a sup of
$p^*$
be a sup of
![]() $\langle p_n:n\in \omega \rangle $
. Then
$\langle p_n:n\in \omega \rangle $
. Then
![]() $p^*\in \operatorname {dom}(\varphi ^{M_\alpha })$
since it is also a sup of
$p^*\in \operatorname {dom}(\varphi ^{M_\alpha })$
since it is also a sup of
![]() $\langle p_{2n+1}:n\in \omega \rangle $
, and
$\langle p_{2n+1}:n\in \omega \rangle $
, and
![]() $p^*\in \operatorname {dom}(\varphi ^{M_\beta })$
since it is a sup of
$p^*\in \operatorname {dom}(\varphi ^{M_\beta })$
since it is a sup of
![]() $\langle p_{2n}:n>0\rangle $
.
$\langle p_{2n}:n>0\rangle $
.
For (2), fix a condition
![]() $q_{-1}\in \mathbb {P}^*$
which extends both
$q_{-1}\in \mathbb {P}^*$
which extends both
![]() $p^*(M_\alpha )$
and
$p^*(M_\alpha )$
and
![]() $p^*(M_\beta )$
, where by (1) we may assume that
$p^*(M_\beta )$
, where by (1) we may assume that
![]() $q_{-1}\in \operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta })$
. We first make a cosmetic improvement to
$q_{-1}\in \operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta })$
. We first make a cosmetic improvement to
![]() $q_{-1}$
before the main construction. Since
$q_{-1}$
before the main construction. Since
![]() $q_{-1}$
extends both
$q_{-1}$
extends both
![]() $\varphi ^{M_\beta }(q_{-1})$
and
$\varphi ^{M_\beta }(q_{-1})$
and
![]() $p^*(M_\alpha )$
and since both of these conditions are in
$p^*(M_\alpha )$
and since both of these conditions are in
![]() $M_\beta $
(using Definition 2.8(2) to see that
$M_\beta $
(using Definition 2.8(2) to see that
![]() $p^*(M_\alpha )\in M_\beta $
), we may apply the elementarity of
$p^*(M_\alpha )\in M_\beta $
), we may apply the elementarity of
![]() $M_\beta $
to find a condition
$M_\beta $
to find a condition
![]() $s_{-1}\in M_\beta $
which extends
$s_{-1}\in M_\beta $
which extends
![]() $\varphi ^{M_\beta }(q_{-1})$
and
$\varphi ^{M_\beta }(q_{-1})$
and
![]() $p^*(M_\alpha )$
. Now, find an extension
$p^*(M_\alpha )$
. Now, find an extension
![]() $q_0\geq q_{-1}$
so that
$q_0\geq q_{-1}$
so that
![]() $\varphi ^{M_\beta }(q_0)\geq s_{-1}$
, noting that we may assume that
$\varphi ^{M_\beta }(q_0)\geq s_{-1}$
, noting that we may assume that
![]() $q_0\in \operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta })$
.
$q_0\in \operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta })$
.
Having completed this modification, we now define, by recursion, an increasing sequence of conditions
![]() $\langle q_n:n\in \omega \rangle $
in
$\langle q_n:n\in \omega \rangle $
in
![]() $\operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta })$
and an increasing sequence
$\operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta })$
and an increasing sequence
![]() $\langle s_n:n\in \omega \rangle $
of conditions in
$\langle s_n:n\in \omega \rangle $
of conditions in
![]() $M_\beta \cap \operatorname {dom}(\varphi ^{M_\alpha })$
so that for each n,
$M_\beta \cap \operatorname {dom}(\varphi ^{M_\alpha })$
so that for each n,
![]() $\varphi ^{M_\beta }(q_{n+1})\geq s_n\geq \varphi ^{M_\beta }(q_n)$
. So assume that
$\varphi ^{M_\beta }(q_{n+1})\geq s_n\geq \varphi ^{M_\beta }(q_n)$
. So assume that
![]() $q_n$
is defined. Since
$q_n$
is defined. Since
![]() $\varphi ^{M_\beta }(q_n)\geq p^*(M_\alpha )$
(using the previous paragraph for the case
$\varphi ^{M_\beta }(q_n)\geq p^*(M_\alpha )$
(using the previous paragraph for the case
![]() $n=0$
), we may find an extension
$n=0$
), we may find an extension
![]() $s_n$
of
$s_n$
of
![]() $\varphi ^{M_\beta }(q_n)$
which is a member of
$\varphi ^{M_\beta }(q_n)$
which is a member of
![]() $M_\beta \cap \operatorname {dom}(\varphi ^{M_\alpha })$
. Then let
$M_\beta \cap \operatorname {dom}(\varphi ^{M_\alpha })$
. Then let
![]() $q_{n+1}\geq q_n$
be a condition with
$q_{n+1}\geq q_n$
be a condition with
![]() $\varphi ^{M_\beta }(q_{n+1})\geq s_n$
. Finally, let
$\varphi ^{M_\beta }(q_{n+1})\geq s_n$
. Finally, let
![]() $q^*$
be a sup of
$q^*$
be a sup of
![]() $\langle q_n:n\in \omega \rangle $
, and let
$\langle q_n:n\in \omega \rangle $
, and let
![]() $s^*$
be a sup of
$s^*$
be a sup of
![]() $\langle s_n:n\in \omega \rangle $
, noting by the intertwined construction that
$\langle s_n:n\in \omega \rangle $
, noting by the intertwined construction that
![]() $s^*$
is also a sup of
$s^*$
is also a sup of
![]() $\langle \varphi ^{M_\beta }(q_n):n\in \omega \rangle $
. By the countable continuity of the residue functions, we have
$\langle \varphi ^{M_\beta }(q_n):n\in \omega \rangle $
. By the countable continuity of the residue functions, we have
![]() $\varphi ^{M_\beta }(q^*)=^*s^*$
. However,
$\varphi ^{M_\beta }(q^*)=^*s^*$
. However,
![]() $s^*\in \operatorname {dom}(\varphi ^{M_\alpha })$
, since it is the sup of the increasing sequence
$s^*\in \operatorname {dom}(\varphi ^{M_\alpha })$
, since it is the sup of the increasing sequence
![]() $\langle s_n:n\in \omega \rangle $
of conditions in
$\langle s_n:n\in \omega \rangle $
of conditions in
![]() $\operatorname {dom}(\varphi ^{M_\alpha })$
. Consequently,
$\operatorname {dom}(\varphi ^{M_\alpha })$
. Consequently,
![]() $\varphi ^{M_\beta }(q^*)$
is also in
$\varphi ^{M_\beta }(q^*)$
is also in
![]() $\operatorname {dom}(\varphi ^{M_\alpha })$
. Since
$\operatorname {dom}(\varphi ^{M_\alpha })$
. Since
![]() $q_{-1}$
in
$q_{-1}$
in
![]() $\mathbb {P}^*/\left \{ p^*(M_\alpha ),p^*(M_\beta ) \right \}$
was arbitrary, this completes the proof of (2).▪
$\mathbb {P}^*/\left \{ p^*(M_\alpha ),p^*(M_\beta ) \right \}$
was arbitrary, this completes the proof of (2).▪
Proposition 4.2 Suppose that
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\mathbb {P}^*$
-suitable with residue system
$\mathbb {P}^*$
-suitable with residue system
and let
![]() $\alpha <\beta $
be in
$\alpha <\beta $
be in
![]() $\operatorname {dom}(\vec {M})$
. Then
$\operatorname {dom}(\vec {M})$
. Then
is
![]() $=^*$
-countably closed and dense in
$=^*$
-countably closed and dense in
![]() $\mathbb {P}^*/\left \{ p^*(M_\alpha ),p^*(M_\beta ) \right \}$
.
$\mathbb {P}^*/\left \{ p^*(M_\alpha ),p^*(M_\beta ) \right \}$
.
Proof We begin by observing that if
![]() $q\in D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
, then
$q\in D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
, then
![]() $\varphi ^{M_\alpha }(q)$
extends
$\varphi ^{M_\alpha }(q)$
extends
![]() $\varphi ^{M_\alpha }(\varphi ^{M_\beta }(q))$
. Indeed, since
$\varphi ^{M_\alpha }(\varphi ^{M_\beta }(q))$
. Indeed, since
![]() $q\in \operatorname {dom}(\varphi ^{M_\beta })$
,
$q\in \operatorname {dom}(\varphi ^{M_\beta })$
,
![]() $q\geq \varphi ^{M_\beta }(q)$
, and since
$q\geq \varphi ^{M_\beta }(q)$
, and since
![]() $\varphi ^{M_\alpha }$
is order-preserving and both q and
$\varphi ^{M_\alpha }$
is order-preserving and both q and
![]() $\varphi ^{M_\beta }(q)$
are in
$\varphi ^{M_\beta }(q)$
are in
![]() $\operatorname {dom}(\varphi ^{M_\alpha })$
, we conclude that
$\operatorname {dom}(\varphi ^{M_\alpha })$
, we conclude that
![]() $\varphi ^{M_\alpha }(q)\geq \varphi ^{M_\alpha }(\varphi ^{M_\beta }(q))$
.
$\varphi ^{M_\alpha }(q)\geq \varphi ^{M_\alpha }(\varphi ^{M_\beta }(q))$
.
With this observation in mind, let
![]() $p\in \mathbb {P}^*$
extend both
$p\in \mathbb {P}^*$
extend both
![]() $p^*(M_\alpha )$
and
$p^*(M_\alpha )$
and
![]() $p^*(M_\beta )$
, and by extending further if necessary, we may assume that p is in
$p^*(M_\beta )$
, and by extending further if necessary, we may assume that p is in
![]() $D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
. We will define by recursion an increasing sequence of conditions
$D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
. We will define by recursion an increasing sequence of conditions
![]() $\langle p_n:n\in \omega \rangle $
in
$\langle p_n:n\in \omega \rangle $
in
![]() $D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
with
$D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
with
![]() $p_0=p$
so that for all n,
$p_0=p$
so that for all n,
note that all of the above items are defined, by definition of
![]() $D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
.
$D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
.
Suppose we are given
![]() $p_{n}$
. As observed earlier, since
$p_{n}$
. As observed earlier, since
![]() $p_n\in D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
, we have
$p_n\in D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
, we have
![]() $\varphi ^{M_\alpha }(p_n)\geq \varphi ^{M_\alpha }(\varphi ^{M_\beta }(p_n))$
. Since
$\varphi ^{M_\alpha }(p_n)\geq \varphi ^{M_\alpha }(\varphi ^{M_\beta }(p_n))$
. Since
![]() $\varphi ^{M_\alpha }(p_n)$
extends, in
$\varphi ^{M_\alpha }(p_n)$
extends, in
![]() $M_\alpha $
, the residue of
$M_\alpha $
, the residue of
![]() $\varphi ^{M_\beta }(p_n)$
to
$\varphi ^{M_\beta }(p_n)$
to
![]() $M_\alpha $
, we may find a condition
$M_\alpha $
, we may find a condition
![]() $q\in M_\beta $
extending
$q\in M_\beta $
extending
![]() $\varphi ^{M_\beta }(p_n)$
so that
$\varphi ^{M_\beta }(p_n)$
so that
![]() $\varphi ^{M_\alpha }(q)\geq \varphi ^{M_\alpha }(p_n)$
. Since
$\varphi ^{M_\alpha }(q)\geq \varphi ^{M_\alpha }(p_n)$
. Since
![]() $q\in M_\beta $
extends
$q\in M_\beta $
extends
![]() $\varphi ^{M_\beta }(p_n)$
, there is an
$\varphi ^{M_\beta }(p_n)$
, there is an
![]() $r\geq p_n$
so that
$r\geq p_n$
so that
![]() $\varphi ^{M_\beta }(r)\geq q$
. Finally, let
$\varphi ^{M_\beta }(r)\geq q$
. Finally, let
![]() $p_{n+1}\geq r$
be a condition in
$p_{n+1}\geq r$
be a condition in
![]() $D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
. Then
$D_0(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
. Then
![]() $\varphi ^{M_\beta }(p_{n+1})\geq \varphi ^{M_\beta }(r)\geq q$
, and hence
$\varphi ^{M_\beta }(p_{n+1})\geq \varphi ^{M_\beta }(r)\geq q$
, and hence
![]() $\varphi ^{M_\alpha }(\varphi ^{M_\beta }(p_{n+1}))\geq \varphi ^{M_\alpha }(q)\geq \varphi ^{M_\alpha }(p_n)$
. This completes the construction of the desired sequence.
$\varphi ^{M_\alpha }(\varphi ^{M_\beta }(p_{n+1}))\geq \varphi ^{M_\alpha }(q)\geq \varphi ^{M_\alpha }(p_n)$
. This completes the construction of the desired sequence.
Let
![]() $p^*$
be a sup of
$p^*$
be a sup of
![]() $\langle p_n:n\in \omega \rangle $
. It is straightforward to verify that it witnesses the lemma.▪
$\langle p_n:n\in \omega \rangle $
. It is straightforward to verify that it witnesses the lemma.▪
The last lemma that we will need before turning to the main result of this section is a technical refinement of Lemma 3.9 which isolates circumstances in which for
![]() $\alpha < \beta < \kappa $
as above, we can find splitting pairs
$\alpha < \beta < \kappa $
as above, we can find splitting pairs
![]() $u,v$
for
$u,v$
for
![]() $(M_\alpha ,\rho )$
with the additional property that
$(M_\alpha ,\rho )$
with the additional property that
![]() $u\upharpoonright M_\beta $
and
$u\upharpoonright M_\beta $
and
![]() $v\upharpoonright M_\beta $
also form a splitting pair for
$v\upharpoonright M_\beta $
also form a splitting pair for
![]() $(M_\alpha ,\rho )$
. Moreover,
$(M_\alpha ,\rho )$
. Moreover,
![]() $u\upharpoonright M_\beta $
and
$u\upharpoonright M_\beta $
and
![]() $v\upharpoonright M_\beta $
will split the nodes on levels between
$v\upharpoonright M_\beta $
will split the nodes on levels between
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
in the same way that u and v do. For the statement of the next result, recall the way we denote restriction of (iteration) length
$\beta $
in the same way that u and v do. For the statement of the next result, recall the way we denote restriction of (iteration) length
![]() $p\upharpoonright \xi $
, and restriction in the poset height,
$p\upharpoonright \xi $
, and restriction in the poset height,
![]() $p\upharpoonright M_\alpha $
, from Notation 3.6.
$p\upharpoonright M_\alpha $
, from Notation 3.6.
Lemma 4.3 Suppose that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
and that
$\rho $
and that
![]() $\operatorname {dom}(\vec {M})$
satisfies the conclusion of Corollary 3.13(2). Suppose
$\operatorname {dom}(\vec {M})$
satisfies the conclusion of Corollary 3.13(2). Suppose
![]() $\alpha <\beta $
are both in
$\alpha <\beta $
are both in
![]() $\operatorname {dom}(\vec {M})$
and that
$\operatorname {dom}(\vec {M})$
and that
![]() $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
and
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
and
![]() $\langle p^*(M_\beta ),\varphi ^{M_\beta }\rangle $
are residue pairs for
$\langle p^*(M_\beta ),\varphi ^{M_\beta }\rangle $
are residue pairs for
![]() $(M_\alpha ,\mathbb {P}^*)$
and
$(M_\alpha ,\mathbb {P}^*)$
and
![]() $(M_\beta ,\mathbb {P}^*)$
respectively. Finally, fix a condition
$(M_\beta ,\mathbb {P}^*)$
respectively. Finally, fix a condition
![]() $u\in \mathbb {R}_\rho $
with
$u\in \mathbb {R}_\rho $
with
![]() $p_u\in \operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta })$
. Then there exist a splitting pair
$p_u\in \operatorname {dom}(\varphi ^{M_\alpha })\cap \operatorname {dom}(\varphi ^{M_\beta })$
. Then there exist a splitting pair
![]() $(u^*,v^*)$
for
$(u^*,v^*)$
for
![]() $(\varphi ^{M_\alpha },\rho )$
extending u and a splitting function
$(\varphi ^{M_\alpha },\rho )$
extending u and a splitting function
![]() $\Sigma $
satisfying the following:
$\Sigma $
satisfying the following:
-
(1)
 $p_{u^*}$
and
$p_{u^*}$
and
 $p_{v^*}$
are both in
$p_{v^*}$
are both in
 $E(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
(see Proposition 4.2); and
$E(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
(see Proposition 4.2); and -
(2)
 $(u^*\upharpoonright M_\beta ,v^*\upharpoonright M_\beta )$
is also an
$(u^*\upharpoonright M_\beta ,v^*\upharpoonright M_\beta )$
is also an
 $(M_\alpha ,\rho )$
-splitting pair, and for any tuple
$(M_\alpha ,\rho )$
-splitting pair, and for any tuple
 $(\zeta ,\nu ,m,n)\in \operatorname {dom}(\Sigma )$
so that the mth node of
$(\zeta ,\nu ,m,n)\in \operatorname {dom}(\Sigma )$
so that the mth node of
 $f_{u^*}(\zeta ,\nu )\backslash (\alpha \times \omega _1)$
and the nth node of
$f_{u^*}(\zeta ,\nu )\backslash (\alpha \times \omega _1)$
and the nth node of
 $f_{v^*}(\zeta ,\nu )\backslash (\alpha \times \omega _1)$
are both in
$f_{v^*}(\zeta ,\nu )\backslash (\alpha \times \omega _1)$
are both in
 $M_\beta $
, and
$M_\beta $
, and $$ \begin{align*}(\varphi^{M_\beta}(p_{u^*}),(f_{u^*}\upharpoonright M_\beta)\upharpoonright\zeta)\Vdash_{\mathbb{R}_\zeta}\Sigma(\zeta,\nu,m,n)(L)<_{\dot{T}_\zeta}\theta \end{align*} $$
$$ \begin{align*}(\varphi^{M_\beta}(p_{u^*}),(f_{u^*}\upharpoonright M_\beta)\upharpoonright\zeta)\Vdash_{\mathbb{R}_\zeta}\Sigma(\zeta,\nu,m,n)(L)<_{\dot{T}_\zeta}\theta \end{align*} $$
 $$ \begin{align*}(\varphi^{M_\beta}(p_{v^*}),(f_{v^*}\upharpoonright M_\beta)\upharpoonright\zeta)\Vdash_{\mathbb{R}_\zeta}\Sigma(\zeta,\nu,m,n)(R)<_{\dot{T}_\zeta}\tau. \end{align*} $$
$$ \begin{align*}(\varphi^{M_\beta}(p_{v^*}),(f_{v^*}\upharpoonright M_\beta)\upharpoonright\zeta)\Vdash_{\mathbb{R}_\zeta}\Sigma(\zeta,\nu,m,n)(R)<_{\dot{T}_\zeta}\tau. \end{align*} $$
Proof By Lemma 3.3, we know that
![]() $D(\varphi ^{M_\alpha },\rho )\cap D(\varphi ^{M_\beta },\rho )$
is dense and
$D(\varphi ^{M_\alpha },\rho )\cap D(\varphi ^{M_\beta },\rho )$
is dense and
![]() $=^*$
-countably closed in
$=^*$
-countably closed in
![]() $\mathbb {R}_\rho /\left \{ p^*(M_\alpha ),p^*(M_\beta )\right \}$
. Moreover, by Proposition 4.2 (with the notation from the statement thereof),
$\mathbb {R}_\rho /\left \{ p^*(M_\alpha ),p^*(M_\beta )\right \}$
. Moreover, by Proposition 4.2 (with the notation from the statement thereof),
![]() $E(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
is dense and countably
$E(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
is dense and countably
![]() $=^*$
-closed in
$=^*$
-closed in
![]() $\mathbb {P}^*/\left \{ p^*(M_\alpha ),p^*(M_\beta )\right \}$
. Consequently,
$\mathbb {P}^*/\left \{ p^*(M_\alpha ),p^*(M_\beta )\right \}$
. Consequently,
is dense and countably
![]() $=^*$
-closed in
$=^*$
-closed in
![]() $\mathbb {R}_\rho /\left \{ p^*(M_\alpha ),p^*(M_\beta )\right \}$
. For use later, we also let
$\mathbb {R}_\rho /\left \{ p^*(M_\alpha ),p^*(M_\beta )\right \}$
. For use later, we also let
![]() $E^*(\varphi ^{M_\alpha },\varphi ^{M_\beta },\zeta )$
be defined similarly, with
$E^*(\varphi ^{M_\alpha },\varphi ^{M_\beta },\zeta )$
be defined similarly, with
![]() $\zeta $
replacing
$\zeta $
replacing
![]() $\rho $
in the above definition.
$\rho $
in the above definition.
Let u be as in the assumption of the current lemma. We may extend and relabel if necessary to assume that
![]() $u\in E^*(\varphi ^{M_\alpha },\varphi ^{M_\beta },\rho )$
. We set
$u\in E^*(\varphi ^{M_\alpha },\varphi ^{M_\beta },\rho )$
. We set
![]() $u_0:=v_0:=u$
and
$u_0:=v_0:=u$
and
![]() $w_0:=u\upharpoonright M_\alpha $
. We will now define a coordinatewise increasing sequence of triples
$w_0:=u\upharpoonright M_\alpha $
. We will now define a coordinatewise increasing sequence of triples
![]() ${\langle \langle u_n,v_n,w_n\rangle :n\in \omega \rangle }$
and a sequence of tuples
${\langle \langle u_n,v_n,w_n\rangle :n\in \omega \rangle }$
and a sequence of tuples
![]() $\langle \langle \zeta _n,\nu _n,\theta _n,\tau _n\rangle :n\in \omega \rangle $
(with respect to some bookkeeping device) of tree nodes and ordinals so that the following conditions are satisfied for all n:
$\langle \langle \zeta _n,\nu _n,\theta _n,\tau _n\rangle :n\in \omega \rangle $
(with respect to some bookkeeping device) of tree nodes and ordinals so that the following conditions are satisfied for all n:
-
(1)
 $\#^\rho _{\varphi ^{M_\alpha }}(u_n,v_n,w_n)$
;
$\#^\rho _{\varphi ^{M_\alpha }}(u_n,v_n,w_n)$
; -
(2)
 $u_n,v_n\in D(\varphi ^{M_\beta },\rho )$
;
$u_n,v_n\in D(\varphi ^{M_\beta },\rho )$
; -
(3)
 $\langle \zeta _n,\nu _n\rangle \in \operatorname {dom}(f_{u_n})\cap \operatorname {dom}(f_{v_n})\cap M_\alpha $
, and
$\langle \zeta _n,\nu _n\rangle \in \operatorname {dom}(f_{u_n})\cap \operatorname {dom}(f_{v_n})\cap M_\alpha $
, and
 $\langle \theta _n,\tau _n\rangle \in (f_{u_n}(\zeta _n,\nu _n)\backslash (\alpha \times \omega _1))\times (f_{v_n}(\zeta _n,v_n)\backslash (\alpha \times \omega _1))$
;
$\langle \theta _n,\tau _n\rangle \in (f_{u_n}(\zeta _n,\nu _n)\backslash (\alpha \times \omega _1))\times (f_{v_n}(\zeta _n,v_n)\backslash (\alpha \times \omega _1))$
; -
(4)
 $u_{n+1}$
and
$u_{n+1}$
and
 $v_{n+1}$
split
$v_{n+1}$
split
 $\langle \theta _n,\tau _n\rangle $
below
$\langle \theta _n,\tau _n\rangle $
below
 $\alpha $
in
$\alpha $
in
 $\dot {T}_{\zeta _n}$
, and if
$\dot {T}_{\zeta _n}$
, and if
 $\theta _n$
and
$\theta _n$
and
 $\tau _n$
are both below level
$\tau _n$
are both below level
 $\beta $
, then in fact
$\beta $
, then in fact
 $u_{n+1}\upharpoonright M_\beta $
and
$u_{n+1}\upharpoonright M_\beta $
and
 $v_{n+1}\upharpoonright M_\beta $
split
$v_{n+1}\upharpoonright M_\beta $
split
 $\langle \theta _n,\tau _n\rangle $
below
$\langle \theta _n,\tau _n\rangle $
below
 $\alpha $
in
$\alpha $
in
 $\dot {T}_{\zeta _n}$
. Moreover, in this case, there is a pair of nodes
$\dot {T}_{\zeta _n}$
. Moreover, in this case, there is a pair of nodes
 $\langle \bar {\theta }_n,\bar {\tau }_n\rangle $
below level
$\langle \bar {\theta }_n,\bar {\tau }_n\rangle $
below level
 $\alpha $
which witnesses the splitting for both
$\alpha $
which witnesses the splitting for both
 $u_{n+1}$
and
$u_{n+1}$
and
 $v_{n+1}$
as well as their restrictions to
$v_{n+1}$
as well as their restrictions to
 $M_\beta $
; and
$M_\beta $
; and -
(5)
 $p_{u_n}$
and
$p_{u_n}$
and
 $p_{v_n}$
are in
$p_{v_n}$
are in
 $E(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
.
$E(\varphi ^{M_\alpha },\varphi ^{M_\beta })$
.
For
![]() $n=0$
, we have that (1), (2), and (5) hold because
$n=0$
, we have that (1), (2), and (5) hold because
![]() $u\in E^*(\varphi ^{M_\alpha },\varphi ^{M_\beta },\rho )$
. (3) holds by definition and (4) is vacuous.
$u\in E^*(\varphi ^{M_\alpha },\varphi ^{M_\beta },\rho )$
. (3) holds by definition and (4) is vacuous.
Suppose, then, that we have defined
![]() $u_n,v_n$
, and
$u_n,v_n$
, and
![]() $w_n$
. By Lemma 3.5, we may find extensions
$w_n$
. By Lemma 3.5, we may find extensions
![]() $u^{\prime }_n\geq u_n$
,
$u^{\prime }_n\geq u_n$
,
![]() $v^{\prime }_n\geq v_n$
, and
$v^{\prime }_n\geq v_n$
, and
![]() $w^{\prime }_n\geq w_n$
so that
$w^{\prime }_n\geq w_n$
so that
![]() $\#^\rho _{\varphi ^{M_\alpha }}(u^{\prime }_n,v^{\prime }_n,w^{\prime }_n)$
holds and so that
$\#^\rho _{\varphi ^{M_\alpha }}(u^{\prime }_n,v^{\prime }_n,w^{\prime }_n)$
holds and so that
![]() $u^{\prime }_n$
and
$u^{\prime }_n$
and
![]() $v^{\prime }_n$
split
$v^{\prime }_n$
split
![]() $\langle \theta _n,\tau _n\rangle $
below
$\langle \theta _n,\tau _n\rangle $
below
![]() $\alpha $
in
$\alpha $
in
![]() $\dot {T}_{\zeta _n}$
. Let
$\dot {T}_{\zeta _n}$
. Let
![]() $\bar {\theta }_n$
and
$\bar {\theta }_n$
and
![]() $\bar {\tau }_n$
be nodes below level
$\bar {\tau }_n$
be nodes below level
![]() $\alpha $
which witness the splitting.
$\alpha $
which witness the splitting.
We now define conditions
![]() $u^{***}_n$
,
$u^{***}_n$
,
![]() $v^{***}_n$
, and
$v^{***}_n$
, and
![]() $w^{***}_n$
(the superscript for later notational purposes) which extend, respectively,
$w^{***}_n$
(the superscript for later notational purposes) which extend, respectively,
![]() $u^{\prime }_n\upharpoonright \zeta _n$
,
$u^{\prime }_n\upharpoonright \zeta _n$
,
![]() $v^{\prime }_n\upharpoonright \zeta _n$
, and
$v^{\prime }_n\upharpoonright \zeta _n$
, and
![]() $w^{\prime }_n\upharpoonright \zeta _n$
. If either
$w^{\prime }_n\upharpoonright \zeta _n$
. If either
![]() $\theta _n$
or
$\theta _n$
or
![]() $\tau _n$
are at or above level
$\tau _n$
are at or above level
![]() $\beta $
(namely, outside of
$\beta $
(namely, outside of
![]() $M_\beta $
), then we simply set
$M_\beta $
), then we simply set
![]() $u^{***}_n:=u'\upharpoonright \zeta _n$
,
$u^{***}_n:=u'\upharpoonright \zeta _n$
,
![]() $v^{***}_n:=u'\upharpoonright \zeta _n$
. Since
$v^{***}_n:=u'\upharpoonright \zeta _n$
. Since
![]() $\operatorname {dom}(\vec {M})$
satisfies the conclusion of Corollary 3.13(2), and since
$\operatorname {dom}(\vec {M})$
satisfies the conclusion of Corollary 3.13(2), and since
![]() $\zeta _n\in M_\alpha $
, we may find a dual residue
$\zeta _n\in M_\alpha $
, we may find a dual residue
![]() $w^{***}_n$
of
$w^{***}_n$
of
![]() $u^{***}_n$
and
$u^{***}_n$
and
![]() $v^{***}_n$
to
$v^{***}_n$
to
![]() $M_\alpha $
. This completes the definition of the triple
$M_\alpha $
. This completes the definition of the triple
![]() $(u^{***}_n,v^{***}_n,w^{***}_n)$
in the case that either
$(u^{***}_n,v^{***}_n,w^{***}_n)$
in the case that either
![]() $\theta _n$
or
$\theta _n$
or
![]() $\tau _n$
are at or above level
$\tau _n$
are at or above level
![]() $\beta $
.
$\beta $
.
Suppose on the other hand that
![]() $\theta _n$
and
$\theta _n$
and
![]() $\tau _n$
are both below level
$\tau _n$
are both below level
![]() $\beta $
and therefore are in
$\beta $
and therefore are in
![]() $M_\beta $
. Since
$M_\beta $
. Since
![]() $\operatorname {dom}(\vec {M})$
satisfies the conclusion of Corollary 3.13(2), and since
$\operatorname {dom}(\vec {M})$
satisfies the conclusion of Corollary 3.13(2), and since
![]() $\zeta _n\in M_\alpha \cap \rho $
and
$\zeta _n\in M_\alpha \cap \rho $
and
![]() $\#^{\zeta _n}_{\varphi ^{M_\alpha }}(u^{\prime }_n\upharpoonright \zeta _n,v^{\prime }_n\upharpoonright \zeta _n,w^{\prime }_n\upharpoonright \zeta _n)$
, we may find a condition
$\#^{\zeta _n}_{\varphi ^{M_\alpha }}(u^{\prime }_n\upharpoonright \zeta _n,v^{\prime }_n\upharpoonright \zeta _n,w^{\prime }_n\upharpoonright \zeta _n)$
, we may find a condition
![]() $w^*_n\in M_\alpha \cap \mathbb {R}_{\zeta _n}$
which is a dual residue of
$w^*_n\in M_\alpha \cap \mathbb {R}_{\zeta _n}$
which is a dual residue of
![]() $u^{\prime }_n\upharpoonright \zeta _n$
and
$u^{\prime }_n\upharpoonright \zeta _n$
and
![]() $v^{\prime }_n\upharpoonright \zeta _n$
to
$v^{\prime }_n\upharpoonright \zeta _n$
to
![]() $M_\alpha $
. We next extend
$M_\alpha $
. We next extend
![]() $u^{\prime }_n\upharpoonright \zeta _n$
to a condition which extends not only
$u^{\prime }_n\upharpoonright \zeta _n$
to a condition which extends not only
![]() $w^*_n$
but also some residue to
$w^*_n$
but also some residue to
![]() $M_\beta $
.
$M_\beta $
.
Let
![]() $u^{**}_n$
be an extension in
$u^{**}_n$
be an extension in
![]() $D(\varphi ^{M_\beta },\zeta _n)$
of
$D(\varphi ^{M_\beta },\zeta _n)$
of
![]() $u^{\prime }_n\upharpoonright \zeta _n$
and
$u^{\prime }_n\upharpoonright \zeta _n$
and
![]() $w^*_n$
. By the remarks before Lemma 3.3, we may let
$w^*_n$
. By the remarks before Lemma 3.3, we may let
![]() $\bar {u}^{**}_n\in M_\beta $
be a residue of
$\bar {u}^{**}_n\in M_\beta $
be a residue of
![]() $u^{**}_n$
to
$u^{**}_n$
to
![]() $M_\beta $
in
$M_\beta $
in
![]() $\mathbb {R}_{\zeta _n}$
. Finally, let
$\mathbb {R}_{\zeta _n}$
. Finally, let
![]() $u^{***}_n$
be a condition in
$u^{***}_n$
be a condition in
![]() $D(\varphi ^{M_\beta },\zeta _n)\cap D(\varphi ^{M_\alpha },\zeta _n)$
which extends
$D(\varphi ^{M_\beta },\zeta _n)\cap D(\varphi ^{M_\alpha },\zeta _n)$
which extends
![]() $u_n^{**}$
and
$u_n^{**}$
and
![]() $\bar {u}^{**}_n$
and which satisfies that
$\bar {u}^{**}_n$
and which satisfies that
![]() $u^{***}_n\upharpoonright M_\beta \geq _{\mathbb {R}_{\zeta _n}}\bar {u}^{**}_n$
.
$u^{***}_n\upharpoonright M_\beta \geq _{\mathbb {R}_{\zeta _n}}\bar {u}^{**}_n$
.
By definition of
![]() $\bar {\theta }_n$
above, we know that
$\bar {\theta }_n$
above, we know that
![]() $u^{\prime }_n\upharpoonright \zeta _n\Vdash _{\mathbb {R}_{\zeta _n}}\bar {\theta }_n<_{\dot {T}_{\zeta _n}}\theta _n$
, and hence the extension
$u^{\prime }_n\upharpoonright \zeta _n\Vdash _{\mathbb {R}_{\zeta _n}}\bar {\theta }_n<_{\dot {T}_{\zeta _n}}\theta _n$
, and hence the extension
![]() $u^{**}_n$
of
$u^{**}_n$
of
![]() $u'\upharpoonright \zeta _n$
forces this too. Since
$u'\upharpoonright \zeta _n$
forces this too. Since
![]() $\bar {u}^{**}_n$
is a residue of
$\bar {u}^{**}_n$
is a residue of
![]() $u^{**}_n$
to
$u^{**}_n$
to
![]() $M_\beta $
in
$M_\beta $
in
![]() $\mathbb {R}_{\zeta _n}$
and
$\mathbb {R}_{\zeta _n}$
and
![]() $\bar {\theta }_n$
,
$\bar {\theta }_n$
,
![]() $\theta _n$
are nodes in
$\theta _n$
are nodes in
![]() $M_\beta $
, we conclude that
$M_\beta $
, we conclude that
![]() $\bar {u}^{**}_n$
also forces that
$\bar {u}^{**}_n$
also forces that
![]() $\bar {\theta }_n<_{\dot {T}_{\zeta _n}}\theta _n$
. Finally, since
$\bar {\theta }_n<_{\dot {T}_{\zeta _n}}\theta _n$
. Finally, since
![]() $u^{***}_n\upharpoonright M_\beta $
is a condition (because
$u^{***}_n\upharpoonright M_\beta $
is a condition (because
![]() $u^{***}_n\in D(\varphi ^{M_\beta },\zeta _n)$
) which extends
$u^{***}_n\in D(\varphi ^{M_\beta },\zeta _n)$
) which extends
![]() $\bar {u}^{**}_n$
, we conclude that
$\bar {u}^{**}_n$
, we conclude that
![]() $u^{***}_n\upharpoonright M_\beta $
forces that
$u^{***}_n\upharpoonright M_\beta $
forces that
![]() $\bar {\theta }_n<_{\dot {T}_{\zeta _n}}\theta _n$
. This completes the first round of extensions of
$\bar {\theta }_n<_{\dot {T}_{\zeta _n}}\theta _n$
. This completes the first round of extensions of
![]() $u^{\prime }_n\upharpoonright \zeta _n$
.
$u^{\prime }_n\upharpoonright \zeta _n$
.
We now turn to extending
![]() $v^{\prime }_n\upharpoonright \zeta _n$
. Since
$v^{\prime }_n\upharpoonright \zeta _n$
. Since
![]() $u_n^{***}\in D(\varphi ^{M_\alpha },\zeta _n)$
, we may let
$u_n^{***}\in D(\varphi ^{M_\alpha },\zeta _n)$
, we may let
![]() $w^{**}_n$
be a residue of
$w^{**}_n$
be a residue of
![]() $u^{***}_n$
to
$u^{***}_n$
to
![]() $M_\alpha $
which extends
$M_\alpha $
which extends
![]() $w_n^*$
. Since
$w_n^*$
. Since
![]() $w^{**}_n\geq w_n^*$
and
$w^{**}_n\geq w_n^*$
and
![]() $w_n^*$
is a residue of
$w_n^*$
is a residue of
![]() $v^{\prime }_n\upharpoonright \zeta _n$
to
$v^{\prime }_n\upharpoonright \zeta _n$
to
![]() $M_\alpha $
,
$M_\alpha $
,
![]() $w^{**}_n$
is also a residue of
$w^{**}_n$
is also a residue of
![]() $v^{\prime }_n\upharpoonright \zeta _n$
to
$v^{\prime }_n\upharpoonright \zeta _n$
to
![]() $M_\alpha $
. Applying the same argument as in the previous two paragraphs to
$M_\alpha $
. Applying the same argument as in the previous two paragraphs to
![]() $v^{\prime }_n\upharpoonright \zeta _n$
with
$v^{\prime }_n\upharpoonright \zeta _n$
with
![]() $w^{**}_n$
playing the role of
$w^{**}_n$
playing the role of
![]() $w^*_n$
and with
$w^*_n$
and with
![]() $\bar {\tau }_n$
and
$\bar {\tau }_n$
and
![]() $\tau _n$
playing the respective roles of
$\tau _n$
playing the respective roles of
![]() $\bar {\theta }_n$
and
$\bar {\theta }_n$
and
![]() $\theta _n$
, we may find an extension
$\theta _n$
, we may find an extension
![]() $v^{***}_n$
of
$v^{***}_n$
of
![]() $v^{\prime }_n\upharpoonright \zeta _n$
in
$v^{\prime }_n\upharpoonright \zeta _n$
in
![]() $D(\varphi ^{M_\beta },\zeta _n)\cap D(\varphi ^{M_\alpha },\zeta _n)$
and a condition
$D(\varphi ^{M_\beta },\zeta _n)\cap D(\varphi ^{M_\alpha },\zeta _n)$
and a condition
![]() $w^{***}_n$
so that
$w^{***}_n$
so that
![]() $v^{***}_n\upharpoonright M_\beta $
forces
$v^{***}_n\upharpoonright M_\beta $
forces
![]() $\bar {\tau }_n<_{\dot {T}_{\zeta _n}}\tau _n$
and so that
$\bar {\tau }_n<_{\dot {T}_{\zeta _n}}\tau _n$
and so that
![]() $w^{***}_n$
is a residue of
$w^{***}_n$
is a residue of
![]() $v^{***}_n$
to
$v^{***}_n$
to
![]() $M_\alpha $
in
$M_\alpha $
in
![]() $\mathbb {R}_{\zeta _n}$
which extends
$\mathbb {R}_{\zeta _n}$
which extends
![]() $w^{**}_n$
. Note that since
$w^{**}_n$
. Note that since
![]() $w^{***}_n\geq w^{**}_n$
,
$w^{***}_n\geq w^{**}_n$
,
![]() $w^{***}_n$
is also a residue of
$w^{***}_n$
is also a residue of
![]() $u^{***}_n$
to
$u^{***}_n$
to
![]() $M_\alpha $
in
$M_\alpha $
in
![]() $\mathbb {R}_{\zeta _n}$
.
$\mathbb {R}_{\zeta _n}$
.
To summarize, we now have extensions
![]() $u^{***}_n$
and
$u^{***}_n$
and
![]() $v^{***}_n$
of
$v^{***}_n$
of
![]() $u^{\prime }_n\upharpoonright \zeta _n$
and
$u^{\prime }_n\upharpoonright \zeta _n$
and
![]() $v^{\prime }_n\upharpoonright \zeta _n$
, respectively, which are both in
$v^{\prime }_n\upharpoonright \zeta _n$
, respectively, which are both in
![]() $D(\varphi ^{M_\beta },\rho )$
and which satisfy that
$D(\varphi ^{M_\beta },\rho )$
and which satisfy that
![]() $u^{***}_n\upharpoonright M_\beta $
and
$u^{***}_n\upharpoonright M_\beta $
and
![]() $v^{***}_n\upharpoonright M_\beta $
split
$v^{***}_n\upharpoonright M_\beta $
split
![]() $\langle \theta _n,\tau _n\rangle $
as witnessed by
$\langle \theta _n,\tau _n\rangle $
as witnessed by
![]() $\langle \bar {\theta }_n,\bar {\tau }_n\rangle $
. Moreover,
$\langle \bar {\theta }_n,\bar {\tau }_n\rangle $
. Moreover,
![]() $w^{***}_n$
is a dual residue of
$w^{***}_n$
is a dual residue of
![]() $u^{***}_n$
and
$u^{***}_n$
and
![]() $v^{***}_n$
to
$v^{***}_n$
to
![]() $M_\alpha $
in
$M_\alpha $
in
![]() $\mathbb {R}_{\zeta _n}$
, i.e.,
$\mathbb {R}_{\zeta _n}$
, i.e.,
![]() $*^{\zeta _n}_{\varphi ^{M_\alpha }}(u^{***}_n,v^{***}_n,w^{***}_n)$
. This completes the definition of the triple
$*^{\zeta _n}_{\varphi ^{M_\alpha }}(u^{***}_n,v^{***}_n,w^{***}_n)$
. This completes the definition of the triple
![]() $(u^{***}_n,v^{***}_n,w^{***}_n)$
in the case that
$(u^{***}_n,v^{***}_n,w^{***}_n)$
in the case that
![]() $\theta _n$
and
$\theta _n$
and
![]() $\tau _n$
are below level
$\tau _n$
are below level
![]() $\beta $
.
$\beta $
.
We now apply Lemma 3.4, to find
![]() $u_{n+1}\upharpoonright \zeta _n\geq u^{***}_n$
,
$u_{n+1}\upharpoonright \zeta _n\geq u^{***}_n$
,
![]() $v_{n+1}\upharpoonright \zeta _n\geq v^{***}_n$
, and
$v_{n+1}\upharpoonright \zeta _n\geq v^{***}_n$
, and
![]() $w_{n+1}\upharpoonright \zeta _n\geq w^{***}_n$
so that
$w_{n+1}\upharpoonright \zeta _n\geq w^{***}_n$
so that
![]() $\#^{\zeta _n}_{\varphi ^{M_\alpha }}(u_{n+1}\upharpoonright \zeta _n,v_{n+1}\upharpoonright \zeta _n,w_{n+1}\upharpoonright \zeta _n)$
and so that
$\#^{\zeta _n}_{\varphi ^{M_\alpha }}(u_{n+1}\upharpoonright \zeta _n,v_{n+1}\upharpoonright \zeta _n,w_{n+1}\upharpoonright \zeta _n)$
and so that
![]() $u_{n+1}\upharpoonright \zeta _n,v_{n+1}\upharpoonright \zeta _n\in E^*(\varphi ^{M_\alpha },\varphi ^{M_\beta },\zeta _n)$
. Define
$u_{n+1}\upharpoonright \zeta _n,v_{n+1}\upharpoonright \zeta _n\in E^*(\varphi ^{M_\alpha },\varphi ^{M_\beta },\zeta _n)$
. Define
![]() $u_{n+1}:=(u_{n+1}\upharpoonright \zeta _n)^\frown (u^{\prime }_n\upharpoonright [\zeta _n,\rho ))$
, with
$u_{n+1}:=(u_{n+1}\upharpoonright \zeta _n)^\frown (u^{\prime }_n\upharpoonright [\zeta _n,\rho ))$
, with
![]() $v_{n+1}$
and
$v_{n+1}$
and
![]() $w_{n+1}$
defined similarly.
$w_{n+1}$
defined similarly.
![]() $u_{n+1},v_{n+1}$
, and
$u_{n+1},v_{n+1}$
, and
![]() $w_{n+1}$
then satisfy (1)–(5), completing the successor step of the construction.
$w_{n+1}$
then satisfy (1)–(5), completing the successor step of the construction.
If we now let
![]() $u^*,v^*,w^*$
be sups of their respective sequences, it is straightforward to see that they satisfy the lemma, using (4) to secure the desired splitting function.▪
$u^*,v^*,w^*$
be sups of their respective sequences, it is straightforward to see that they satisfy the lemma, using (4) to secure the desired splitting function.▪
Having laid the groundwork in the previous results, we next turn to analyzing when quotients of
![]() $\mathbb {R}_\rho $
preserve stationary sets of cofinality
$\mathbb {R}_\rho $
preserve stationary sets of cofinality
![]() $\omega $
ordinals. We will prove the following proposition.
$\omega $
ordinals. We will prove the following proposition.
Proposition 4.4 Suppose that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
and that
$\rho $
and that
![]() $\operatorname {dom}(\vec {M})$
satisfies Corollary 3.13(2). Then there exists some
$\operatorname {dom}(\vec {M})$
satisfies Corollary 3.13(2). Then there exists some
![]() $B^*\subseteq \operatorname {dom}(\vec {M})$
with
$B^*\subseteq \operatorname {dom}(\vec {M})$
with
![]() $\operatorname {dom}(\vec {M})\backslash B^*\in \mathcal {I}$
so that for any
$\operatorname {dom}(\vec {M})\backslash B^*\in \mathcal {I}$
so that for any
![]() $\alpha \in B^*$
, any
$\alpha \in B^*$
, any
![]() $(\mathbb {R}_\rho \cap M_\alpha )$
-name
$(\mathbb {R}_\rho \cap M_\alpha )$
-name
![]() $\dot {S}$
for a stationary subset of
$\dot {S}$
for a stationary subset of
![]() $\alpha \cap \operatorname {cof}(\omega )$
, and any residue pair
$\alpha \cap \operatorname {cof}(\omega )$
, and any residue pair
![]() $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
![]() $(M_\alpha ,\mathbb {P}^*)$
, the poset
$(M_\alpha ,\mathbb {P}^*)$
, the poset
![]() $\mathbb {R}_\rho /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\rho })$
forces that
$\mathbb {R}_\rho /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\rho })$
forces that
![]() $\dot {S}$
remains stationary.
$\dot {S}$
remains stationary.
Thus, the quotient forcing of
![]() $\mathbb {R}_\rho $
above the condition
$\mathbb {R}_\rho $
above the condition
![]() $(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\rho })$
preserves the stationarity of
$(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\rho })$
preserves the stationarity of
![]() $\dot {S}$
. The remainder of the section is devoted to the proof.
$\dot {S}$
. The remainder of the section is devoted to the proof.
Proof To begin, we define the set
![]() $B^*:=\operatorname {tr}(B)\cap B$
, where
$B^*:=\operatorname {tr}(B)\cap B$
, where
![]() $B=\operatorname {dom}(\vec {M})$
. Since
$B=\operatorname {dom}(\vec {M})$
. Since
![]() $B\in \mathcal {F}^+$
, Lemma 1.7 implies that
$B\in \mathcal {F}^+$
, Lemma 1.7 implies that
![]() $B\backslash B^*\in \mathcal {I}$
.
$B\backslash B^*\in \mathcal {I}$
.
Now, fix, for the rest of the proof, an ordinal
![]() $\alpha \in B^*$
and a residue pair
$\alpha \in B^*$
and a residue pair
![]() $\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
$\langle p^*(M_\alpha ),\varphi ^{M_\alpha }\rangle $
for
![]() $(M_\alpha ,\mathbb {P}^*)$
; since
$(M_\alpha ,\mathbb {P}^*)$
; since
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
, we may also fix, for each
$\rho $
, we may also fix, for each
![]() $\gamma \in B\cap \alpha $
, a residue pair
$\gamma \in B\cap \alpha $
, a residue pair
![]() $\langle p^*(M_\gamma ),\varphi ^{M_\gamma }\rangle $
for
$\langle p^*(M_\gamma ),\varphi ^{M_\gamma }\rangle $
for
![]() $(M_\gamma ,\mathbb {P}^*)$
.
$(M_\gamma ,\mathbb {P}^*)$
.
Next, fix a condition
![]() $(p,f)$
in
$(p,f)$
in
![]() $\mathbb {R}_\rho /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\rho })$
and an
$\mathbb {R}_\rho /(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\rho })$
and an
![]() $\mathbb {R}_\rho $
-name
$\mathbb {R}_\rho $
-name
![]() $\dot {C}$
for a closed unbounded subset of
$\dot {C}$
for a closed unbounded subset of
![]() $\alpha $
. We will find some extension
$\alpha $
. We will find some extension
![]() $(p^*,f^*)$
of
$(p^*,f^*)$
of
![]() $(p,f)$
which forces in
$(p,f)$
which forces in
![]() $\mathbb {R}_\rho $
that
$\mathbb {R}_\rho $
that
![]() $ \dot {C}\cap \dot {S}\neq \emptyset $
. By Lemma 3.3, we may assume that
$ \dot {C}\cap \dot {S}\neq \emptyset $
. By Lemma 3.3, we may assume that
![]() $(p,f)\in D(\varphi ^{M_\alpha },\rho )$
.
$(p,f)\in D(\varphi ^{M_\alpha },\rho )$
.
In V, let
![]() $\theta>\kappa ^+$
be a large enough regular cardinal, and let
$\theta>\kappa ^+$
be a large enough regular cardinal, and let
![]() $K\prec H(\theta )$
be chosen so that
$K\prec H(\theta )$
be chosen so that
![]() $|K|=\kappa $
,
$|K|=\kappa $
,
![]() $\,^{<\kappa }K\subseteq K$
, and so that K has the following parameters as elements:
$\,^{<\kappa }K\subseteq K$
, and so that K has the following parameters as elements:
-
(i) the sequences
 $\vec {M}$
and
$\vec {M}$
and
 $\langle \langle p^*(M_\gamma ),\varphi ^{M_\gamma }\rangle :\gamma \in B\cap (\alpha +1)\rangle $
, the set
$\langle \langle p^*(M_\gamma ),\varphi ^{M_\gamma }\rangle :\gamma \in B\cap (\alpha +1)\rangle $
, the set
 $B^*$
, the poset
$B^*$
, the poset
 $\mathbb {R}_\rho $
, the
$\mathbb {R}_\rho $
, the
 $\mathbb {R}_\rho $
-condition
$\mathbb {R}_\rho $
-condition
 $(p,f)$
, the
$(p,f)$
, the
 $\mathbb {R}_\rho $
-name
$\mathbb {R}_\rho $
-name
 $\dot {C}$
, and the
$\dot {C}$
, and the
 $(\mathbb {R}_\rho \cap M_\alpha )$
-name
$(\mathbb {R}_\rho \cap M_\alpha )$
-name
 $\dot {S}$
; and
$\dot {S}$
; and -
(ii) the fixed well-order
 $\lhd $
of
$\lhd $
of
 $H(\kappa ^+)$
from Notation 2.6.
$H(\kappa ^+)$
from Notation 2.6.
Finally, let
![]() $\mathbb {K}$
denote the tuple
$\mathbb {K}$
denote the tuple
![]() $(K,\in ,\alpha ,\vec {M},B^*,\mathbb {R}_\rho ,(p,f),\dot {C},\dot {S},\lhd ). $
$(K,\in ,\alpha ,\vec {M},B^*,\mathbb {R}_\rho ,(p,f),\dot {C},\dot {S},\lhd ). $
Define
![]() $E_0$
to be the club of
$E_0$
to be the club of
![]() $\beta <\alpha $
so that
$\beta <\alpha $
so that
![]() $\operatorname {Sk}^{\mathbb {K}}(\beta )\cap \alpha =\beta $
. Since
$\operatorname {Sk}^{\mathbb {K}}(\beta )\cap \alpha =\beta $
. Since
![]() $\alpha \in B^*$
, we know that
$\alpha \in B^*$
, we know that
![]() $B\cap \alpha $
is stationary in
$B\cap \alpha $
is stationary in
![]() $\alpha $
. Thus,
$\alpha $
. Thus,
![]() $B\cap \lim (B)\cap \alpha $
is stationary in
$B\cap \lim (B)\cap \alpha $
is stationary in
![]() $\alpha $
, and therefore
$\alpha $
, and therefore
![]() $E:=\lim (E_0\cap B)$
is a club in
$E:=\lim (E_0\cap B)$
is a club in
![]() $\alpha $
.
$\alpha $
.
Recalling that
![]() $(p,f)\in D(\varphi ^{M_\alpha },\rho )$
, we can find a residue
$(p,f)\in D(\varphi ^{M_\alpha },\rho )$
, we can find a residue
![]() $(\bar {p},\bar {f})$
of
$(\bar {p},\bar {f})$
of
![]() $(p,f)$
to
$(p,f)$
to
![]() $M_\alpha $
which extends the condition
$M_\alpha $
which extends the condition
![]() $(\varphi ^{M_\alpha }(p),f\upharpoonright M_\alpha )$
. Let
$(\varphi ^{M_\alpha }(p),f\upharpoonright M_\alpha )$
. Let
![]() $\dot {X}$
be the
$\dot {X}$
be the
![]() $(\mathbb {R}_\rho \cap M_\alpha )$
-name for
$(\mathbb {R}_\rho \cap M_\alpha )$
-name for
by Lemma 2.13, we know that
![]() $\dot {X}$
is forced by
$\dot {X}$
is forced by
![]() $\mathbb {R}_\rho \cap M_\alpha $
to be unbounded in
$\mathbb {R}_\rho \cap M_\alpha $
to be unbounded in
![]() $\alpha $
. Since
$\alpha $
. Since
![]() $\dot {S}$
is an
$\dot {S}$
is an
![]() $(\mathbb {R}_\rho \cap M_\alpha )$
-name of a stationary subset of
$(\mathbb {R}_\rho \cap M_\alpha )$
-name of a stationary subset of
![]() $\alpha \cap \operatorname {cof}(\omega )$
,
$\alpha \cap \operatorname {cof}(\omega )$
,
![]() $\dot {S}$
is forced to contain a limit point of
$\dot {S}$
is forced to contain a limit point of
![]() $\dot {X}$
. This, combined with the fact that
$\dot {X}$
. This, combined with the fact that
![]() $\mathbb {R}_\rho \cap M_\alpha $
does not add new
$\mathbb {R}_\rho \cap M_\alpha $
does not add new
![]() $\omega $
-sequences, implies that we can find an extension
$\omega $
-sequences, implies that we can find an extension
![]() $(q,g)\geq _{\mathbb {R}_\rho \cap M_\alpha }(\bar {p},\bar {f})$
and an increasing sequence
$(q,g)\geq _{\mathbb {R}_\rho \cap M_\alpha }(\bar {p},\bar {f})$
and an increasing sequence
![]() $\langle \beta _n:n\in \omega \rangle $
in
$\langle \beta _n:n\in \omega \rangle $
in
![]() $E_0\cap B{\cap \lim (B)}$
with
$E_0\cap B{\cap \lim (B)}$
with
![]() $\sup _n\beta _n = \nu \in E \cap \operatorname {cof}(\omega )$
, so that (i)
$\sup _n\beta _n = \nu \in E \cap \operatorname {cof}(\omega )$
, so that (i)
![]() $(q,g)\Vdash _{\mathbb {R}_\rho \cap M_\alpha }\nu \in \dot {S}$
, and (ii) for all
$(q,g)\Vdash _{\mathbb {R}_\rho \cap M_\alpha }\nu \in \dot {S}$
, and (ii) for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $q\geq _{\mathbb {P}^*} p^*(M_{\beta _n})$
.
$q\geq _{\mathbb {P}^*} p^*(M_{\beta _n})$
.
For the rest of the proof, we will fix
![]() $(q,g) \in \mathbb {R}_\rho \cap M_\alpha $
,
$(q,g) \in \mathbb {R}_\rho \cap M_\alpha $
,
![]() $\langle \beta _n \mid n< \omega \rangle $
, and
$\langle \beta _n \mid n< \omega \rangle $
, and
![]() $\nu $
with the above properties. Define
$\nu $
with the above properties. Define
![]() $ K_{\beta _n}:=\operatorname {Sk}^{\mathbb {K}}(\beta _n), $
noting that
$ K_{\beta _n}:=\operatorname {Sk}^{\mathbb {K}}(\beta _n), $
noting that
![]() $K_{\beta _n}\cap \alpha =\beta _n$
because
$K_{\beta _n}\cap \alpha =\beta _n$
because
![]() $\beta _n\in E_0$
. It will be helpful for later to see that
$\beta _n\in E_0$
. It will be helpful for later to see that
![]() $M_{\beta _n}\subseteq K_{\beta _n}$
for each n. Indeed,
$M_{\beta _n}\subseteq K_{\beta _n}$
for each n. Indeed,
![]() $\beta _n\in B\cap \lim (B)$
which implies that
$\beta _n\in B\cap \lim (B)$
which implies that
![]() $M_{\beta _n}=\bigcup _{\eta \in B\cap \beta _n}M_\eta $
. Moreover,
$M_{\beta _n}=\bigcup _{\eta \in B\cap \beta _n}M_\eta $
. Moreover,
![]() $\beta _n\subseteq K_{\beta _n}$
, and therefore applying the elementarity of
$\beta _n\subseteq K_{\beta _n}$
, and therefore applying the elementarity of
![]() $K_{\beta _n}$
, we see that for all
$K_{\beta _n}$
, we see that for all
![]() $\eta \in B\cap \beta _n$
,
$\eta \in B\cap \beta _n$
,
![]() $M_\eta \in K_{\beta _n}$
. Since
$M_\eta \in K_{\beta _n}$
. Since
![]() $\beta _n\subseteq K_{\beta _n}$
,
$\beta _n\subseteq K_{\beta _n}$
,
![]() $\eta \subseteq K_{\beta _n}$
too. Thus,
$\eta \subseteq K_{\beta _n}$
too. Thus,
![]() $M_\eta \subseteq K_{\beta _n}$
since
$M_\eta \subseteq K_{\beta _n}$
since
![]() $K_{\beta _n}$
sees a bijection between
$K_{\beta _n}$
sees a bijection between
![]() $M_\eta $
and
$M_\eta $
and
![]() $\eta $
. Combining all of this, we see that
$\eta $
. Combining all of this, we see that
![]() $M_{\beta _n}=\bigcup _{\eta \in B\cap \beta _n}M_\eta \subseteq K_{\beta _n}$
.
$M_{\beta _n}=\bigcup _{\eta \in B\cap \beta _n}M_\eta \subseteq K_{\beta _n}$
.
We proceed to find an extension
![]() $(p^*,f^*)$
of
$(p^*,f^*)$
of
![]() $(p,f)$
which is compatible with
$(p,f)$
which is compatible with
![]() $(q,g)$
and forces that
$(q,g)$
and forces that
![]() $\nu \in \dot {C}$
. We will secure this by building two increasing
$\nu \in \dot {C}$
. We will secure this by building two increasing
![]() $\omega $
-sequences of conditions, one above
$\omega $
-sequences of conditions, one above
![]() $(p,f)$
and another above
$(p,f)$
and another above
![]() $(q,g)$
, in such a way that the limits of each sequence can be amalgamated; the resulting condition will then force
$(q,g)$
, in such a way that the limits of each sequence can be amalgamated; the resulting condition will then force
![]() $\nu $
into
$\nu $
into
![]() $\dot {S}\cap \dot {C}$
. Let
$\dot {S}\cap \dot {C}$
. Let
![]() $(p_0,f_0):=(p,f)$
and
$(p_0,f_0):=(p,f)$
and
![]() $(q_0,g_0):=(q,g)$
.
$(q_0,g_0):=(q,g)$
.
Claim 4.1 There exists an increasing sequence
![]() $\langle (p_n,f_n):n\in \omega \rangle $
of conditions in
$\langle (p_n,f_n):n\in \omega \rangle $
of conditions in
![]() $\mathbb {R}_\rho $
and an increasing sequence
$\mathbb {R}_\rho $
and an increasing sequence
![]() $\langle (q_n,g_n):n\in \omega \rangle $
of conditions in
$\langle (q_n,g_n):n\in \omega \rangle $
of conditions in
![]() $\mathbb {R}_\rho \cap M_\alpha $
so that for each
$\mathbb {R}_\rho \cap M_\alpha $
so that for each
![]() $n\in \omega $
,
$n\in \omega $
,
-
(1)
 $(p_n,f_n)\in K_{\beta _n}$
;
$(p_n,f_n)\in K_{\beta _n}$
; -
(2)
 $(p_{n+1},f_{n+1})\Vdash _{\mathbb {R}_\rho }\dot {C}\cap (\beta _n,\nu )\neq \emptyset $
;
$(p_{n+1},f_{n+1})\Vdash _{\mathbb {R}_\rho }\dot {C}\cap (\beta _n,\nu )\neq \emptyset $
; -
(3)
 $(p_n,f_n)\in D(\varphi ^{M_\alpha },\rho )$
;
$(p_n,f_n)\in D(\varphi ^{M_\alpha },\rho )$
; -
(4)
 $q_n\geq _{{\mathbb {P}^*}\cap M_\alpha }\varphi ^{M_\alpha }(p_n)$
; and
$q_n\geq _{{\mathbb {P}^*}\cap M_\alpha }\varphi ^{M_\alpha }(p_n)$
; and -
(5)
 $f_{n+1}$
and
$f_{n+1}$
and
 $g_{n+1}$
are strongly compatible (Definition 3.10) over
$g_{n+1}$
are strongly compatible (Definition 3.10) over
 $p_{n+1}$
and
$p_{n+1}$
and
 $q_{n+1}$
.▪
$q_{n+1}$
.▪
Before we prove this claim, we show that proving it suffices to obtain the desired condition
![]() $(p^*,f^*)$
. So suppose that Claim 4.1 is true. Let
$(p^*,f^*)$
. So suppose that Claim 4.1 is true. Let
![]() $(p^*,f^*)$
be a sup of
$(p^*,f^*)$
be a sup of
![]() $\langle (p_n,f_n):n\in \omega \rangle $
, and let
$\langle (p_n,f_n):n\in \omega \rangle $
, and let
![]() $(q^*,g^*)$
be a sup of
$(q^*,g^*)$
be a sup of
![]() $\langle (q_n,g_n):n\in \omega \rangle $
.
$\langle (q_n,g_n):n\in \omega \rangle $
.
Observe that by item (2) of Claim 4.1 and the fact that the sequence
![]() $\langle \beta _n:n\in \omega \rangle $
is cofinal in
$\langle \beta _n:n\in \omega \rangle $
is cofinal in
![]() $\nu $
, we have that
$\nu $
, we have that
![]() $(p^*,f^*)\Vdash _{\mathbb {R}_\rho }\nu \in \lim (\dot {C})$
and hence forces that
$(p^*,f^*)\Vdash _{\mathbb {R}_\rho }\nu \in \lim (\dot {C})$
and hence forces that
![]() $\nu \in \dot {C}$
as
$\nu \in \dot {C}$
as
![]() $\dot {C}$
names a club. Furthermore, since
$\dot {C}$
names a club. Furthermore, since
![]() $(q^*,g^*)\geq (q_0,g_0)$
and since
$(q^*,g^*)\geq (q_0,g_0)$
and since
![]() $(q_0,g_0)=(q,g)$
forces that
$(q_0,g_0)=(q,g)$
forces that
![]() $\nu \in \dot {S}$
,
$\nu \in \dot {S}$
,
![]() $(q^*,g^*)$
forces that
$(q^*,g^*)$
forces that
![]() $\nu \in \dot {S}$
too. We claim that
$\nu \in \dot {S}$
too. We claim that
![]() $p^*$
and
$p^*$
and
![]() $q^*$
are compatible in
$q^*$
are compatible in
![]() $\mathbb {P}^*$
, from which it follows by item (5) of Claim 4.1 that
$\mathbb {P}^*$
, from which it follows by item (5) of Claim 4.1 that
![]() $f^*$
and
$f^*$
and
![]() $g^*$
are strongly compatible over
$g^*$
are strongly compatible over
![]() $p^*$
and
$p^*$
and
![]() $q^*$
. Indeed,
$q^*$
. Indeed,
![]() $(p^*,f^*)\in D(\varphi ^{M_\alpha },\rho )$
since this set is closed under sups of increasing
$(p^*,f^*)\in D(\varphi ^{M_\alpha },\rho )$
since this set is closed under sups of increasing
![]() $\omega $
-sequences by Lemma 3.3. Furthermore, by the countable continuity of
$\omega $
-sequences by Lemma 3.3. Furthermore, by the countable continuity of
![]() $\varphi ^{M_\alpha }$
,
$\varphi ^{M_\alpha }$
,
![]() $\varphi ^{M_\alpha }(p^*)$
is a sup of the increasing sequence
$\varphi ^{M_\alpha }(p^*)$
is a sup of the increasing sequence
![]() $\langle \varphi ^{M_\alpha }(p_n):n\in \omega \rangle $
. Thus, to show that
$\langle \varphi ^{M_\alpha }(p_n):n\in \omega \rangle $
. Thus, to show that
![]() $p^*$
and
$p^*$
and
![]() $q^*$
are compatible, since
$q^*$
are compatible, since
![]() $q^*\in \mathbb {P}^*\cap M_\alpha $
, it suffices to show that
$q^*\in \mathbb {P}^*\cap M_\alpha $
, it suffices to show that
![]() $q^*\geq _{\mathbb {P}^*\cap M_\alpha }\varphi ^{M_\alpha }(p^*)$
. However, we know that
$q^*\geq _{\mathbb {P}^*\cap M_\alpha }\varphi ^{M_\alpha }(p^*)$
. However, we know that
![]() $q^*\geq q_n$
for all n and so by (4) of Claim 4.1,
$q^*\geq q_n$
for all n and so by (4) of Claim 4.1,
![]() $q^*\geq \varphi ^{M_\alpha }(p_n)$
for all n. Therefore,
$q^*\geq \varphi ^{M_\alpha }(p_n)$
for all n. Therefore,
![]() $q^*$
extends
$q^*$
extends
![]() $\varphi ^{M_\alpha }(p^*)$
, by definition of a supremum.
$\varphi ^{M_\alpha }(p^*)$
, by definition of a supremum.
Now, let
![]() $(p^{**},f^{**})$
be a condition in
$(p^{**},f^{**})$
be a condition in
![]() $\mathbb {R}_\rho $
above both
$\mathbb {R}_\rho $
above both
![]() $(p^*,f^*)$
and
$(p^*,f^*)$
and
![]() $(q^*,g^*)$
. Then, because
$(q^*,g^*)$
. Then, because
![]() $(p^{**},f^{**})$
extends
$(p^{**},f^{**})$
extends
![]() $(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\rho })$
as well as
$(p^*(M_\alpha ),0_{\dot {\mathbb {S}}_\rho })$
as well as
![]() $(q^*,g^*)$
, which in turn forces in
$(q^*,g^*)$
, which in turn forces in
![]() $\mathbb {R}_\rho \cap M_\alpha $
that
$\mathbb {R}_\rho \cap M_\alpha $
that
![]() $\nu \in \dot {S}$
, we have that
$\nu \in \dot {S}$
, we have that
![]() $(p^{**},f^{**})\Vdash _{\mathbb {R}_\rho }\nu \in \dot {S}$
. And finally, as
$(p^{**},f^{**})\Vdash _{\mathbb {R}_\rho }\nu \in \dot {S}$
. And finally, as
![]() $(p^{**},f^{**})$
extends
$(p^{**},f^{**})$
extends
![]() $(p^*,f^*)$
which forces in
$(p^*,f^*)$
which forces in
![]() $\mathbb {R}_\rho $
that
$\mathbb {R}_\rho $
that
![]() $\nu \in \dot {C}$
, we conclude that
$\nu \in \dot {C}$
, we conclude that
![]() $(p^{**},f^{**})\Vdash _{\mathbb {R}_\rho }\nu \in \dot {S}\cap \dot {C}$
. Thus, it suffices to prove Claim 4.1 in order to finish the proof of Proposition 4.4.
$(p^{**},f^{**})\Vdash _{\mathbb {R}_\rho }\nu \in \dot {S}\cap \dot {C}$
. Thus, it suffices to prove Claim 4.1 in order to finish the proof of Proposition 4.4.
Proof of Claim 4.5
We will construct the sequences satisfying (1)–(5) of Claim 4.1 recursively. For the base case
![]() $n=0$
, items (2) and (5) hold vacuously. For item (1), we have that
$n=0$
, items (2) and (5) hold vacuously. For item (1), we have that
![]() $(p_0,f_0)=(p,f)\in K_{\beta _0}$
as
$(p_0,f_0)=(p,f)\in K_{\beta _0}$
as
![]() $(p,f)=(p_0,f_0)$
was chosen to be definable by a constant in the language of
$(p,f)=(p_0,f_0)$
was chosen to be definable by a constant in the language of
![]() $\mathbb {K}$
. We also ensured that
$\mathbb {K}$
. We also ensured that
![]() $(p_0,f_0)\in D(\varphi ^{M_\alpha },\rho )$
, which establishes (3). Finally,
$(p_0,f_0)\in D(\varphi ^{M_\alpha },\rho )$
, which establishes (3). Finally,
![]() $ q_0\geq _{\mathbb {P}^*\cap M_\alpha }\bar {p}\geq _{\mathbb {P}^*\cap M_\alpha }\varphi ^{M_\alpha }(p_0), $
which establishes (4).
$ q_0\geq _{\mathbb {P}^*\cap M_\alpha }\bar {p}\geq _{\mathbb {P}^*\cap M_\alpha }\varphi ^{M_\alpha }(p_0), $
which establishes (4).
Suppose, then, that we have defined
![]() $(p_n,f_n)$
and
$(p_n,f_n)$
and
![]() $(q_n,g_n)$
satisfying (1)–(5). We first observe that
$(q_n,g_n)$
satisfying (1)–(5). We first observe that
![]() $(p_n,f_n)$
and
$(p_n,f_n)$
and
![]() $(q_n,g_n)$
are compatible. If
$(q_n,g_n)$
are compatible. If
![]() $n=0$
, this holds since
$n=0$
, this holds since
![]() $(q_0,g_0)$
is in
$(q_0,g_0)$
is in
![]() $\mathbb {R}_\rho \cap M_\alpha $
and extends
$\mathbb {R}_\rho \cap M_\alpha $
and extends
![]() $(\bar {p},\bar {f})$
, which is a residue of
$(\bar {p},\bar {f})$
, which is a residue of
![]() $(p_0,f_0)$
to
$(p_0,f_0)$
to
![]() $\mathbb {R}_\rho \cap M_\alpha $
. If
$\mathbb {R}_\rho \cap M_\alpha $
. If
![]() $n>0$
, then we have that
$n>0$
, then we have that
![]() $q_n\geq _{\mathbb {P}^*\cap M_\alpha }\varphi ^{M_\alpha }(p_n)$
, and therefore
$q_n\geq _{\mathbb {P}^*\cap M_\alpha }\varphi ^{M_\alpha }(p_n)$
, and therefore
![]() $p_n$
and
$p_n$
and
![]() $q_n$
are
$q_n$
are
![]() $\mathbb {P}^*$
-compatible. Moreover,
$\mathbb {P}^*$
-compatible. Moreover,
![]() $f_n$
and
$f_n$
and
![]() $g_n$
are strongly compatible over the compatible conditions
$g_n$
are strongly compatible over the compatible conditions
![]() $p_n$
and
$p_n$
and
![]() $q_n$
, and therefore
$q_n$
, and therefore
![]() $(p_n,f_n)$
and
$(p_n,f_n)$
and
![]() $(q_n,g_n)$
are compatible in
$(q_n,g_n)$
are compatible in
![]() $\mathbb {R}_\rho $
.
$\mathbb {R}_\rho $
.
Next, choose some condition
![]() $(r,h)$
in
$(r,h)$
in
![]() $\mathbb {R}_\rho $
which extends
$\mathbb {R}_\rho $
which extends
![]() $(p_n,f_n)$
and
$(p_n,f_n)$
and
![]() $(q_n,g_n)$
, and by extending if necessary, we may assume that there is some ordinal
$(q_n,g_n)$
, and by extending if necessary, we may assume that there is some ordinal
![]() $\mu>\beta _n$
so that
$\mu>\beta _n$
so that
![]() $(r,h)\Vdash _{\mathbb {R}_\rho }\mu \in \dot {C}\backslash (\beta _n+1)$
. Since
$(r,h)\Vdash _{\mathbb {R}_\rho }\mu \in \dot {C}\backslash (\beta _n+1)$
. Since
![]() $r\geq p_n\geq p^*(M_\alpha )$
and since
$r\geq p_n\geq p^*(M_\alpha )$
and since
![]() $r\geq q_n\geq q_0\geq p^*(M_{\beta _{n+1}})$
, we may also extend if necessary to assume, by Lemma 4.1(1), that
$r\geq q_n\geq q_0\geq p^*(M_{\beta _{n+1}})$
, we may also extend if necessary to assume, by Lemma 4.1(1), that
![]() $r\in \operatorname {dom}(\varphi ^{M_{\beta _{n+1}}})\cap \operatorname {dom}(\varphi ^{M_\alpha })$
and also that
$r\in \operatorname {dom}(\varphi ^{M_{\beta _{n+1}}})\cap \operatorname {dom}(\varphi ^{M_\alpha })$
and also that
![]() $\varphi ^{M_\alpha }(r)\geq q_n$
.
$\varphi ^{M_\alpha }(r)\geq q_n$
.
We now apply Lemma 4.3, with
![]() $\alpha $
and
$\alpha $
and
![]() $\beta _{n+1}$
playing the respective roles of “
$\beta _{n+1}$
playing the respective roles of “
![]() $\beta $
” and “
$\beta $
” and “
![]() $\alpha $
” in the statement thereof, to find extensions
$\alpha $
” in the statement thereof, to find extensions
![]() $(r_L,h_L)$
and
$(r_L,h_L)$
and
![]() $(r_R,h_R)$
of
$(r_R,h_R)$
of
![]() $(r,h)$
which satisfy the conclusion of that lemma. We let
$(r,h)$
which satisfy the conclusion of that lemma. We let
![]() $(\bar {r},\bar {h})$
be a condition so that
$(\bar {r},\bar {h})$
be a condition so that
![]() $\#^\rho _{\varphi ^{M_{\beta _{n+1}}}}((r_L,h_L),(r_R,h_R),(\bar {r},\bar {h}))$
.
$\#^\rho _{\varphi ^{M_{\beta _{n+1}}}}((r_L,h_L),(r_R,h_R),(\bar {r},\bar {h}))$
.
Let
![]() $\Sigma $
be a splitting function for
$\Sigma $
be a splitting function for
![]() $(r_L,h_L)$
and
$(r_L,h_L)$
and
![]() $(r_R,h_R)$
with respect to the model
$(r_R,h_R)$
with respect to the model
![]() $M_{\beta _{n+1}}$
which satisfies Lemma 4.3. For
$M_{\beta _{n+1}}$
which satisfies Lemma 4.3. For
![]() $Z\in \left \{ L,R\right \}$
, set
$Z\in \left \{ L,R\right \}$
, set
this is a countable subset of
![]() $M_{\beta _{n+1}}$
and therefore is a member of
$M_{\beta _{n+1}}$
and therefore is a member of
![]() $M_{\beta _{n+1}}$
. Since
$M_{\beta _{n+1}}$
. Since
![]() $M_{\beta _{n+1}}\subseteq K_{\beta _{n+1}}$
, as shown earlier,
$M_{\beta _{n+1}}\subseteq K_{\beta _{n+1}}$
, as shown earlier,
![]() $x_Z$
is also an element of
$x_Z$
is also an element of
![]() $K_{\beta _{n+1}}$
.
$K_{\beta _{n+1}}$
.
We are now in a position to reflect into the model
![]() $K_{\beta _{n+1}}$
. We observe that in
$K_{\beta _{n+1}}$
. We observe that in
![]() $H(\theta )$
the following statement is true in the following parameters
$H(\theta )$
the following statement is true in the following parameters
![]() $\beta _n,\Sigma ,\bar {r},\bar {h}, \mathbb {R}_\rho , (p_n,f_n), \alpha $
,
$\beta _n,\Sigma ,\bar {r},\bar {h}, \mathbb {R}_\rho , (p_n,f_n), \alpha $
,
![]() $B, \dot {C}, x_L$
,
$B, \dot {C}, x_L$
,
![]() $x_R$
,
$x_R$
,
![]() $\vec {M}$
, and
$\vec {M}$
, and
![]() $\langle \langle p^*(M_\gamma ),\varphi ^{M_\gamma }\rangle :\gamma \in B\cap (\alpha +1)\rangle $
, all of which are in
$\langle \langle p^*(M_\gamma ),\varphi ^{M_\gamma }\rangle :\gamma \in B\cap (\alpha +1)\rangle $
, all of which are in
![]() $ K_{\beta _{n+1}}$
: there exist a condition
$ K_{\beta _{n+1}}$
: there exist a condition
![]() $(r^*,h^*)$
in
$(r^*,h^*)$
in
![]() $\mathbb {R}_\rho $
and a pair
$\mathbb {R}_\rho $
and a pair
![]() $(r^*_Z,h^*_Z)_{Z\in \left \{ L,R\right \}}$
of conditions above
$(r^*_Z,h^*_Z)_{Z\in \left \{ L,R\right \}}$
of conditions above
![]() $(r^*,h^*)$
in
$(r^*,h^*)$
in
![]() $\mathbb {R}_\rho $
as well as ordinals
$\mathbb {R}_\rho $
as well as ordinals
![]() $\mu ^*,\eta $
, so that:
$\mu ^*,\eta $
, so that:
-
(i)
 $(r^*,h^*)\geq _{\mathbb {R}_\rho } (p_n,f_n)$
;
$(r^*,h^*)\geq _{\mathbb {R}_\rho } (p_n,f_n)$
; -
(ii)
 $\eta \in B$
;
$\eta \in B$
; -
(iii)
 $\#^\rho _{\varphi ^{M_\eta }} ((r^*_L,h^*_L),(r^*_R,h^*_R),(\bar {r},\bar {h}))$
;
$\#^\rho _{\varphi ^{M_\eta }} ((r^*_L,h^*_L),(r^*_R,h^*_R),(\bar {r},\bar {h}))$
; -
(iv) for each
 $Z\in \left \{ L,R\right \}$
,
$Z\in \left \{ L,R\right \}$
,
 $(r^*_Z,h^*_Z)$
and
$(r^*_Z,h^*_Z)$
and
 $(r^*,h^*)$
are in
$(r^*,h^*)$
are in
 $E^*(\varphi ^{M_\eta },\varphi ^{M_\alpha })$
(see Proposition 4.2);
$E^*(\varphi ^{M_\eta },\varphi ^{M_\alpha })$
(see Proposition 4.2); -
(v)
 $(r^*,h^*)\Vdash _{\mathbb {R}_\rho }\mu ^*\in \dot {C}\backslash (\beta _n+1)$
;
$(r^*,h^*)\Vdash _{\mathbb {R}_\rho }\mu ^*\in \dot {C}\backslash (\beta _n+1)$
; -
(vi)
 $\operatorname {dom}(h^*_Z)\cap M_\eta =x_Z$
; and
$\operatorname {dom}(h^*_Z)\cap M_\eta =x_Z$
; and -
(vii)
 $(r^*_L,h^*_L)$
and
$(r^*_L,h^*_L)$
and
 $(r^*_R,h^*_R)$
are an
$(r^*_R,h^*_R)$
are an
 $(M_\eta ,\rho )$
-splitting pair, and
$(M_\eta ,\rho )$
-splitting pair, and
 $\Sigma $
is a splitting function for
$\Sigma $
is a splitting function for
 $(r^*_L,h^*_L)$
and
$(r^*_L,h^*_L)$
and
 $(r^*_R,h^*_R)$
with respect to the model
$(r^*_R,h^*_R)$
with respect to the model
 $M_\eta $
.
$M_\eta $
.
This statement is true in
![]() $H(\theta )$
as witnessed by the conditions
$H(\theta )$
as witnessed by the conditions
![]() $(r_Z,h_Z)_{Z\in \left \{ L,R\right \}}$
and
$(r_Z,h_Z)_{Z\in \left \{ L,R\right \}}$
and
![]() $(r,h)$
, the ordinal
$(r,h)$
, the ordinal
![]() $\mu $
playing the role of
$\mu $
playing the role of
![]() $\mu ^*$
, and the ordinal
$\mu ^*$
, and the ordinal
![]() $\beta _{n+1}$
playing the role of
$\beta _{n+1}$
playing the role of
![]() $\eta $
. Since the parameters of this statement are in
$\eta $
. Since the parameters of this statement are in
![]() $K_{\beta _{n+1}}$
, we may therefore find, in
$K_{\beta _{n+1}}$
, we may therefore find, in
![]() $K_{\beta _{n+1}}$
, conditions
$K_{\beta _{n+1}}$
, conditions
![]() $(r^*_Z,h^*_Z)_{Z\in \left \{ L,R\right \}}$
extending some
$(r^*_Z,h^*_Z)_{Z\in \left \{ L,R\right \}}$
extending some
![]() $(r^*,h^*)\geq (p_n,f_n)$
, an ordinal
$(r^*,h^*)\geq (p_n,f_n)$
, an ordinal
![]() $\mu ^*$
, and an ordinal
$\mu ^*$
, and an ordinal
![]() $\eta \in B$
so that (i)–(vii) above are satisfied of these objects.
$\eta \in B$
so that (i)–(vii) above are satisfied of these objects.
We now define
![]() $(p_{n+1},f_{n+1}):=(r^*_L,h^*_L)$
. We need to extend the condition
$(p_{n+1},f_{n+1}):=(r^*_L,h^*_L)$
. We need to extend the condition
![]() $(\varphi ^{M_{\alpha }}(r_R),h_R\upharpoonright M_\alpha )$
a bit more before defining
$(\varphi ^{M_{\alpha }}(r_R),h_R\upharpoonright M_\alpha )$
a bit more before defining
![]() $(q_{n+1},g_{n+1})$
. The following claim will help us do this.
$(q_{n+1},g_{n+1})$
. The following claim will help us do this.
Subclaim 4.2
![]() $\varphi ^{M_\alpha }(p_{n+1})$
and
$\varphi ^{M_\alpha }(p_{n+1})$
and
![]() $\varphi ^{M_\alpha }(r_R)$
are compatible in
$\varphi ^{M_\alpha }(r_R)$
are compatible in
![]() $\mathbb {P}^*\cap M_\alpha $
.▪
$\mathbb {P}^*\cap M_\alpha $
.▪
Proof Both the condition
![]() $p_{n+1}$
and the function
$p_{n+1}$
and the function
![]() $\varphi ^{M_\alpha }$
are members of
$\varphi ^{M_\alpha }$
are members of
![]() $K_{\beta _{n+1}}$
. Therefore,
$K_{\beta _{n+1}}$
. Therefore,
![]() $\varphi ^{M_\alpha }(p_{n+1})\in K_{\beta _{n+1}}\cap M_\alpha \cap \mathbb {P}^*$
. Recall that
$\varphi ^{M_\alpha }(p_{n+1})\in K_{\beta _{n+1}}\cap M_\alpha \cap \mathbb {P}^*$
. Recall that
![]() $\mathbb {K}$
contained the fixed well-order
$\mathbb {K}$
contained the fixed well-order
![]() $\lhd $
of
$\lhd $
of
![]() $H(\kappa ^+)$
and that all suitable models are elementary in
$H(\kappa ^+)$
and that all suitable models are elementary in
![]() $H(\kappa ^+)$
with respect to
$H(\kappa ^+)$
with respect to
![]() $\lhd $
. Thus, if we let
$\lhd $
. Thus, if we let
![]() $e^{\mathbb {P}^*}$
denote the
$e^{\mathbb {P}^*}$
denote the
![]() $\lhd $
-least bijection from
$\lhd $
-least bijection from
![]() $\kappa $
onto
$\kappa $
onto
![]() $\mathbb {P}^*$
, then we have that
$\mathbb {P}^*$
, then we have that
![]() $e^{\mathbb {P}^*}$
is in
$e^{\mathbb {P}^*}$
is in
![]() $M_\alpha $
and in
$M_\alpha $
and in
![]() $K_{\beta _{n+1}}$
. Since
$K_{\beta _{n+1}}$
. Since
![]() $M_\alpha $
is elementary and contains
$M_\alpha $
is elementary and contains
![]() $e^{\mathbb {P}^*}$
, we see that
$e^{\mathbb {P}^*}$
, we see that
![]() $\varphi ^{M_\alpha }(p_{n+1})=e^{\mathbb {P}^*}(\zeta )$
for some
$\varphi ^{M_\alpha }(p_{n+1})=e^{\mathbb {P}^*}(\zeta )$
for some
![]() $\zeta <\alpha $
. But then, by the elementarity of
$\zeta <\alpha $
. But then, by the elementarity of
![]() $K_{\beta _{n+1}}$
, we see that
$K_{\beta _{n+1}}$
, we see that
![]() $\zeta \in K_{\beta _{n+1}}\cap \alpha =\beta _{n+1}$
. Therefore,
$\zeta \in K_{\beta _{n+1}}\cap \alpha =\beta _{n+1}$
. Therefore,
![]() $\varphi ^{M_\alpha }(p_{n+1})=e^{\mathbb {P}^*}(\zeta )\in M_{\beta _{n+1}}$
. Furthermore, we know that
$\varphi ^{M_\alpha }(p_{n+1})=e^{\mathbb {P}^*}(\zeta )\in M_{\beta _{n+1}}$
. Furthermore, we know that
where the first equality holds by definition of
![]() $\bar {r}$
and the second because
$\bar {r}$
and the second because
![]() $r_R$
satisfies Lemma 4.3. Applying (iii) and (iv) above, we also have that
$r_R$
satisfies Lemma 4.3. Applying (iii) and (iv) above, we also have that
In addition, since
![]() $\varphi ^{M_\eta }$
is an exact, strong residue function and
$\varphi ^{M_\eta }$
is an exact, strong residue function and
![]() $\varphi ^{M_\alpha }(p_{n+1})\in \operatorname {dom}(\varphi ^{M_\eta })$
, we know that
$\varphi ^{M_\alpha }(p_{n+1})\in \operatorname {dom}(\varphi ^{M_\eta })$
, we know that
Therefore, as
![]() $\varphi ^{M_\alpha }(p_{n+1})\in M_{\beta _{n+1}}$
extends
$\varphi ^{M_\alpha }(p_{n+1})\in M_{\beta _{n+1}}$
extends
![]() $\bar {r}$
, which is a residue of
$\bar {r}$
, which is a residue of
![]() $\varphi ^{M_\alpha }(r_R)$
to
$\varphi ^{M_\alpha }(r_R)$
to
![]() $M_{\beta _{n+1}}$
, we conclude that
$M_{\beta _{n+1}}$
, we conclude that
![]() $\varphi ^{M_\alpha }(p_{n+1})$
is compatible with
$\varphi ^{M_\alpha }(p_{n+1})$
is compatible with
![]() $\varphi ^{M_\alpha }(r_R)$
in
$\varphi ^{M_\alpha }(r_R)$
in
![]() $\mathbb {P}^*\cap M_\alpha $
.▪(Subclaim 4.2)
$\mathbb {P}^*\cap M_\alpha $
.▪(Subclaim 4.2)
Using Subclaim 4.2, we may fix some condition
![]() $q_{n+1}$
in
$q_{n+1}$
in
![]() $\mathbb {P}^*\cap M_\alpha $
which is above both
$\mathbb {P}^*\cap M_\alpha $
which is above both
![]() $\varphi ^{M_\alpha }(p_{n+1})$
and
$\varphi ^{M_\alpha }(p_{n+1})$
and
![]() $\varphi ^{M_\alpha }(r_R)$
. We finally set
$\varphi ^{M_\alpha }(r_R)$
. We finally set
![]() $g_{n+1}:=h_R\upharpoonright M_\alpha $
, noting that
$g_{n+1}:=h_R\upharpoonright M_\alpha $
, noting that
![]() $(q_{n+1},g_{n+1})\in M_\alpha $
.
$(q_{n+1},g_{n+1})\in M_\alpha $
.
We next verify that items (1)–(5) of Claim 4.1 hold for
![]() $n+1$
. We have that
$n+1$
. We have that
![]() $(p_{n+1},f_{n+1})\geq (p_n,f_n)$
by (i) of the reflection, more precisely, since
$(p_{n+1},f_{n+1})\geq (p_n,f_n)$
by (i) of the reflection, more precisely, since
In addition, because
we have that
![]() $q_{n+1}\geq q_n$
. Moreover,
$q_{n+1}\geq q_n$
. Moreover,
![]() $g_{n+1}$
extends
$g_{n+1}$
extends
![]() $g_n$
as a function:
$g_n$
as a function:
![]() $g_{n+1}=h_R\upharpoonright M_\alpha $
,
$g_{n+1}=h_R\upharpoonright M_\alpha $
,
![]() $g_n\in M_\alpha $
, and
$g_n\in M_\alpha $
, and
![]() $(r_R,h_R)\geq (r,h)\geq (q_n,g_n)$
. Thus,
$(r_R,h_R)\geq (r,h)\geq (q_n,g_n)$
. Thus,
![]() $(q_{n+1},g_{n+1})$
extends
$(q_{n+1},g_{n+1})$
extends
![]() $(q_n,g_n)$
. (1) of Claim 4.1 holds because we found the witnesses in the model
$(q_n,g_n)$
. (1) of Claim 4.1 holds because we found the witnesses in the model
![]() $K_{\beta _{n+1}}$
. For (2),
$K_{\beta _{n+1}}$
. For (2),
![]() $\mu ^*\in K_{\beta _{n+1}}\cap \alpha =\beta _{n+1}\subseteq \nu $
, and since
$\mu ^*\in K_{\beta _{n+1}}\cap \alpha =\beta _{n+1}\subseteq \nu $
, and since
![]() $\mu ^*>\beta _n$
, we have that
$\mu ^*>\beta _n$
, we have that
![]() $(p_{n+1},f_{n+1})\Vdash \mu ^*\in \dot {C}\cap (\beta _n,\nu )$
. For (3), we have
$(p_{n+1},f_{n+1})\Vdash \mu ^*\in \dot {C}\cap (\beta _n,\nu )$
. For (3), we have
![]() $(p_{n+1},f_{n+1})\in D(\varphi ^{M_\alpha },\rho )$
by (iii) and the definition of
$(p_{n+1},f_{n+1})\in D(\varphi ^{M_\alpha },\rho )$
by (iii) and the definition of
![]() $\#^\rho _{\varphi ^{M_\eta }}$
(see Definition 3.7). For (4), we have that
$\#^\rho _{\varphi ^{M_\eta }}$
(see Definition 3.7). For (4), we have that
![]() $q_{n+1}\geq \varphi ^{M_\alpha }(p_{n+1})$
by choice of
$q_{n+1}\geq \varphi ^{M_\alpha }(p_{n+1})$
by choice of
![]() $q_{n+1}$
.
$q_{n+1}$
.
It remains therefore to check that item (5) of Claim 4.1 holds. Since
![]() $q_{n+1}\geq _{\mathbb {P}^*\cap M_\alpha }\varphi ^{M_\alpha }(p_{n+1})$
, we know that
$q_{n+1}\geq _{\mathbb {P}^*\cap M_\alpha }\varphi ^{M_\alpha }(p_{n+1})$
, we know that
![]() $p_{n+1}$
and
$p_{n+1}$
and
![]() $q_{n+1}$
are compatible in
$q_{n+1}$
are compatible in
![]() $\mathbb {P}^*$
; let
$\mathbb {P}^*$
; let
![]() $p^*\in \mathbb {P}^*$
be any condition extending both. We claim that
$p^*\in \mathbb {P}^*$
be any condition extending both. We claim that
Suppose by induction on
![]() $\delta <\rho $
that
$\delta <\rho $
that
![]() $\langle \delta ,\nu \rangle \in \operatorname {dom}(f_{n+1})\cap \operatorname {dom}(g_{n+1})$
and that
$\langle \delta ,\nu \rangle \in \operatorname {dom}(f_{n+1})\cap \operatorname {dom}(g_{n+1})$
and that
![]() $p^*$
forces that the union of
$p^*$
forces that the union of
![]() $\check {f}_{n+1}\upharpoonright \delta $
and
$\check {f}_{n+1}\upharpoonright \delta $
and
![]() $\check {g}_{n+1}\upharpoonright \delta $
is a condition in
$\check {g}_{n+1}\upharpoonright \delta $
is a condition in
![]() $\dot {\mathbb {S}}_\delta $
. Again using the fixed well-order
$\dot {\mathbb {S}}_\delta $
. Again using the fixed well-order
![]() $\lhd $
of
$\lhd $
of
![]() $H(\kappa ^+)$
, we may let
$H(\kappa ^+)$
, we may let
![]() $\psi $
be the
$\psi $
be the
![]() $\lhd $
-least bijection from
$\lhd $
-least bijection from
![]() $\kappa $
onto
$\kappa $
onto
![]() $\rho $
, so that
$\rho $
, so that
![]() $\psi $
is a member of
$\psi $
is a member of
![]() $K_{\beta _{n+1}}$
as well as every model on the
$K_{\beta _{n+1}}$
as well as every model on the
![]() $\mathbb {R}_\rho $
-suitable sequence
$\mathbb {R}_\rho $
-suitable sequence
![]() $\vec {M}$
. Since
$\vec {M}$
. Since
![]() $\langle \delta ,\nu \rangle \in \operatorname {dom}(g_{n+1})$
and
$\langle \delta ,\nu \rangle \in \operatorname {dom}(g_{n+1})$
and
![]() $g_{n+1}\in M_\alpha $
,
$g_{n+1}\in M_\alpha $
,
![]() $\delta \in M_\alpha \cap \rho =\psi [\alpha ]$
. Furthermore, since
$\delta \in M_\alpha \cap \rho =\psi [\alpha ]$
. Furthermore, since
![]() $\langle \delta ,\nu \rangle \in \operatorname {dom}(f_{n+1})$
and
$\langle \delta ,\nu \rangle \in \operatorname {dom}(f_{n+1})$
and
![]() $f_{n+1}=h^*_L\in K_{\beta _{n+1}}$
, we have that
$f_{n+1}=h^*_L\in K_{\beta _{n+1}}$
, we have that
![]() $\delta \in K_{\beta _{n+1}}$
. Thus,
$\delta \in K_{\beta _{n+1}}$
. Thus,
Therefore (recalling that
![]() $g_{n+1}=h_R\upharpoonright M_\alpha $
),
$g_{n+1}=h_R\upharpoonright M_\alpha $
),
Continuing, fix a pair
with
![]() $\theta \neq \tau $
. We need to show that
$\theta \neq \tau $
. We need to show that
![]() $\theta $
and
$\theta $
and
![]() $\tau $
are forced to be incompatible nodes in the tree
$\tau $
are forced to be incompatible nodes in the tree
![]() $\dot {T}_\delta $
by the condition
$\dot {T}_\delta $
by the condition
![]() $\big (p^*,(f_{n+1}\cup g_{n+1})\upharpoonright \delta \big )$
. Recall, going forward, that
$\big (p^*,(f_{n+1}\cup g_{n+1})\upharpoonright \delta \big )$
. Recall, going forward, that
![]() $(\bar {r},\bar {h})$
equals both
$(\bar {r},\bar {h})$
equals both
![]() $(r_R,h_R)\upharpoonright M_{\beta _{n+1}}$
and
$(r_R,h_R)\upharpoonright M_{\beta _{n+1}}$
and
![]() $(p_{n+1},f_{n+1})\upharpoonright M_\eta $
; in particular,
$(p_{n+1},f_{n+1})\upharpoonright M_\eta $
; in particular,
![]() $f_{n+1}$
and
$f_{n+1}$
and
![]() $h_R\upharpoonright M_\alpha =g_{n+1}$
both extend
$h_R\upharpoonright M_\alpha =g_{n+1}$
both extend
![]() $\bar {h}$
. Continuing, if
$\bar {h}$
. Continuing, if
![]() $\tau $
is below level
$\tau $
is below level
![]() $\beta _{n+1}$
, then
$\beta _{n+1}$
, then
![]() $\tau \in \bar {h}(\delta ,\nu )\subseteq f_{n+1}(\delta ,\nu )$
and we are done. Furthermore, if
$\tau \in \bar {h}(\delta ,\nu )\subseteq f_{n+1}(\delta ,\nu )$
and we are done. Furthermore, if
![]() $\theta $
is below level
$\theta $
is below level
![]() $\eta $
, then
$\eta $
, then
![]() $\theta \in \bar {h}(\delta ,\nu )\subseteq g_{n+1}(\delta ,\nu )$
and we are done in this case too. Thus, we assume that
$\theta \in \bar {h}(\delta ,\nu )\subseteq g_{n+1}(\delta ,\nu )$
and we are done in this case too. Thus, we assume that
![]() $\theta $
is at or above level
$\theta $
is at or above level
![]() $\eta $
and that
$\eta $
and that
![]() $\tau $
is at or above level
$\tau $
is at or above level
![]() $\beta _{n+1}$
. With respect to the fixed enumerations, let k and m be chosen so that
$\beta _{n+1}$
. With respect to the fixed enumerations, let k and m be chosen so that
![]() $\theta $
is the kth element of
$\theta $
is the kth element of
![]() $f_{n+1}(\delta ,\nu )\backslash (\eta \times \omega _1)$
and
$f_{n+1}(\delta ,\nu )\backslash (\eta \times \omega _1)$
and
![]() $\tau $
is the mth element of
$\tau $
is the mth element of
![]() $h_R(\delta ,\nu )\backslash (\beta _{n+1}\times \omega _1)$
. Then, because the function
$h_R(\delta ,\nu )\backslash (\beta _{n+1}\times \omega _1)$
. Then, because the function
![]() $\Sigma $
is the same for both pairs of splitting conditions, we know that
$\Sigma $
is the same for both pairs of splitting conditions, we know that
and that
However,
![]() $\tau \in g_{n+1}(\delta ,\nu )=(h_R\upharpoonright M_\alpha )(\delta ,\nu )$
, and therefore
$\tau \in g_{n+1}(\delta ,\nu )=(h_R\upharpoonright M_\alpha )(\delta ,\nu )$
, and therefore
![]() $\tau $
is below level
$\tau $
is below level
![]() $\alpha $
of the tree
$\alpha $
of the tree
![]() $\dot {T}_\delta $
. Therefore, by Lemma 4.3, we have that
$\dot {T}_\delta $
. Therefore, by Lemma 4.3, we have that
Since
![]() $q_{n+1}\geq \varphi ^{M_\alpha }(r_R)$
and
$q_{n+1}\geq \varphi ^{M_\alpha }(r_R)$
and
![]() $g_{n+1}=h_R\upharpoonright M_\alpha $
, we conclude that
$g_{n+1}=h_R\upharpoonright M_\alpha $
, we conclude that
Finally, since
![]() $\big (p^*,(f_{n+1}\cup g_{n+1})\upharpoonright \delta \big )$
is above both
$\big (p^*,(f_{n+1}\cup g_{n+1})\upharpoonright \delta \big )$
is above both
![]() $(p_{n+1},f_{n+1}\upharpoonright \delta )$
and
$(p_{n+1},f_{n+1}\upharpoonright \delta )$
and
![]() ${(q_{n+1},g_{n+1}\upharpoonright \delta )}$
, it follows that
${(q_{n+1},g_{n+1}\upharpoonright \delta )}$
, it follows that
Since the distinct nodes
![]() $\Sigma (\delta ,\nu ,k,m)(L)$
and
$\Sigma (\delta ,\nu ,k,m)(L)$
and
![]() $\Sigma (\delta ,\nu ,k,m)(R)$
are on the same level,
$\Sigma (\delta ,\nu ,k,m)(R)$
are on the same level,
![]() $\big (p^*,(f_{n+1}\cup g_{n+1})\upharpoonright \delta \big )$
therefore forces that
$\big (p^*,(f_{n+1}\cup g_{n+1})\upharpoonright \delta \big )$
therefore forces that
![]() $\theta $
and
$\theta $
and
![]() $\tau $
are incompatible nodes in the tree
$\tau $
are incompatible nodes in the tree
![]() $\dot {T}_\delta $
.
$\dot {T}_\delta $
.
This completes the proof that
![]() $f_{n+1}$
and
$f_{n+1}$
and
![]() $g_{n+1}$
are strongly compatible over
$g_{n+1}$
are strongly compatible over
![]() $p_{n+1}$
and
$p_{n+1}$
and
![]() $q_{n+1}$
. Therefore, the proof of Claim 4.1 is now complete.▪(Claim 4.1)
$q_{n+1}$
. Therefore, the proof of Claim 4.1 is now complete.▪(Claim 4.1)
As remarked earlier, this completes the proof of Proposition 4.4.
Remark 4.5 As we have noted before, if
![]() $\mathbb {P}^*$
is just equal to the collapse poset
$\mathbb {P}^*$
is just equal to the collapse poset
![]() $\mathbb {P}$
, then the results from Section 3 which are needed for this section hold only assuming that
$\mathbb {P}$
, then the results from Section 3 which are needed for this section hold only assuming that
![]() $\kappa $
is weakly compact (since then
$\kappa $
is weakly compact (since then
![]() $\mathcal {F}=\mathcal {F}_{WC}$
; see Definition 2.8). We then see that if
$\mathcal {F}=\mathcal {F}_{WC}$
; see Definition 2.8). We then see that if
![]() $\mathbb {P}^*$
is just
$\mathbb {P}^*$
is just
![]() $\mathbb {P}$
, then the arguments in this section can also be carried out only using a weakly compact.
$\mathbb {P}$
, then the arguments in this section can also be carried out only using a weakly compact.
As a corollary of Proposition 4.4, we can now prove Theorem 1.2.
Proof Recall that the Laver–Shelah model
![]() $V[G*F]$
is obtained by starting from a ground model V with a weakly compact cardinal
$V[G*F]$
is obtained by starting from a ground model V with a weakly compact cardinal
![]() $\kappa $
, and forcing with the Levy collapse
$\kappa $
, and forcing with the Levy collapse
![]() $\mathbb {P}$
followed by a countable support iteration
$\mathbb {P}$
followed by a countable support iteration
![]() $\mathbb {S} = \langle \mathbb {S}_\tau ,\mathbb {S}(\tau )\mid \tau < \kappa ^+\rangle $
of specializing posets
$\mathbb {S} = \langle \mathbb {S}_\tau ,\mathbb {S}(\tau )\mid \tau < \kappa ^+\rangle $
of specializing posets
![]() $\mathbb {S}(\tau ) = \mathbb {S}(\dot {T_\tau })$
of Aronszajn trees on
$\mathbb {S}(\tau ) = \mathbb {S}(\dot {T_\tau })$
of Aronszajn trees on
![]() $\kappa $
, chosen by a bookkeeping function. Since
$\kappa $
, chosen by a bookkeeping function. Since
![]() $\mathbb {S}$
satisfies the
$\mathbb {S}$
satisfies the
![]() $\kappa $
-c.c, every sequence of stationary sets
$\kappa $
-c.c, every sequence of stationary sets
![]() $\langle S_\alpha \mid \alpha < \kappa \rangle $
as in the statement of Theorem 1.2 belongs to an intermediate extension
$\langle S_\alpha \mid \alpha < \kappa \rangle $
as in the statement of Theorem 1.2 belongs to an intermediate extension
![]() $V[G*F_\tau ]$
, where
$V[G*F_\tau ]$
, where
![]() $F_\tau := F \cap \mathbb {S}_\tau $
, for some
$F_\tau := F \cap \mathbb {S}_\tau $
, for some
![]() $\tau <\kappa ^+$
. Now, work in V, and take a
$\tau <\kappa ^+$
. Now, work in V, and take a
![]() $(\mathbb {P}*\dot {\mathbb {S}}_\tau )$
-name
$(\mathbb {P}*\dot {\mathbb {S}}_\tau )$
-name
![]() $\langle \dot {S}_\alpha \mid \alpha < \kappa \rangle $
for the sequence of stationary sets. Let
$\langle \dot {S}_\alpha \mid \alpha < \kappa \rangle $
for the sequence of stationary sets. Let
![]() $\vec {M}$
be suitable with respect to these parameters. By the weak compactness of
$\vec {M}$
be suitable with respect to these parameters. By the weak compactness of
![]() $\kappa $
, let
$\kappa $
, let
![]() $\beta \in \operatorname {dom}(\vec {M})$
be such that
$\beta \in \operatorname {dom}(\vec {M})$
be such that
![]() $\langle \dot {S}_\alpha \cap V_\beta \mid \alpha < \beta \rangle $
are names for stationary subsets of
$\langle \dot {S}_\alpha \cap V_\beta \mid \alpha < \beta \rangle $
are names for stationary subsets of
![]() $\beta $
in the restricted poset
$\beta $
in the restricted poset
![]() $(\mathbb {P} * \dot {\mathbb {S}}_\tau )\cap M_\beta $
. Recalling Remark 4.5, we see that Proposition 4.4 can be applied to
$(\mathbb {P} * \dot {\mathbb {S}}_\tau )\cap M_\beta $
. Recalling Remark 4.5, we see that Proposition 4.4 can be applied to
![]() $\mathbb {P}$
, and in this case,
$\mathbb {P}$
, and in this case,
![]() $\mathcal {F}=\mathcal {F}_{WC}$
. We conclude that each
$\mathcal {F}=\mathcal {F}_{WC}$
. We conclude that each
![]() $S_\alpha \cap \beta $
remains stationary in the full
$S_\alpha \cap \beta $
remains stationary in the full
![]() $\mathbb {P} * \dot {\mathbb {S}}_\tau $
generic extension
$\mathbb {P} * \dot {\mathbb {S}}_\tau $
generic extension
![]() $V[G*F_\tau ]$
and hence in
$V[G*F_\tau ]$
and hence in
![]() $V[G\ast F]$
.
$V[G\ast F]$
.
To see that
![]() $\mathsf {CSR}(\omega _2)$
fails in the Laver–Shelah model, observe that in the ground model, there exist stationary sets
$\mathsf {CSR}(\omega _2)$
fails in the Laver–Shelah model, observe that in the ground model, there exist stationary sets
![]() $S\subseteq \kappa \cap \operatorname {cof}(\omega )$
and
$S\subseteq \kappa \cap \operatorname {cof}(\omega )$
and
![]() $T\subseteq \kappa \cap \operatorname {cof}(\omega _1)$
so that S does not reflect at any point in T (see Proposition 1.1 of [Reference Jech and Shelah22]). The stationarity of S and T are preserved by the
$T\subseteq \kappa \cap \operatorname {cof}(\omega _1)$
so that S does not reflect at any point in T (see Proposition 1.1 of [Reference Jech and Shelah22]). The stationarity of S and T are preserved by the
![]() $\kappa $
-c.c. forcing of Laver and Shelah, and since
$\kappa $
-c.c. forcing of Laver and Shelah, and since
![]() $\omega _1$
is also preserved, we have that S and T witness the failure of
$\omega _1$
is also preserved, we have that S and T witness the failure of
![]() $\mathsf {CSR}(\omega _2)$
in the final model.▪
$\mathsf {CSR}(\omega _2)$
in the final model.▪
5
 $\mathcal {F}$
-completely proper posets
$\mathcal {F}$
-completely proper posets
In this section, we will specify what
![]() $\mathbb {P}$
-names
$\mathbb {P}$
-names
![]() $\dot {\mathbb {C}}$
for posets are such that
$\dot {\mathbb {C}}$
for posets are such that
![]() $\mathbb {P}\ast \dot {\mathbb {C}}$
is
$\mathbb {P}\ast \dot {\mathbb {C}}$
is
![]() ${\mathcal {F}}$
-strongly proper, and we will draw some conclusions from this. Since
${\mathcal {F}}$
-strongly proper, and we will draw some conclusions from this. Since
![]() $\mathbb {P}\ast \dot {\mathbb {C}}$
will be playing the role of
$\mathbb {P}\ast \dot {\mathbb {C}}$
will be playing the role of
![]() $\mathbb {P}^*$
in Definition 2.8, and since
$\mathbb {P}^*$
in Definition 2.8, and since
![]() $\mathbb {P}\ast \dot {\mathbb {C}}$
is not merely the collapse, we are in the case when
$\mathbb {P}\ast \dot {\mathbb {C}}$
is not merely the collapse, we are in the case when
![]() $\kappa $
is ineffable and
$\kappa $
is ineffable and
![]() $\mathcal {F}=\mathcal {F}_{in}$
. However, we only use the ineffability of
$\mathcal {F}=\mathcal {F}_{in}$
. However, we only use the ineffability of
![]() $\kappa $
in the following section when applying Proposition 3.12 through its use in Proposition 4.4. Recall Definition 2.8 for the definition of
$\kappa $
in the following section when applying Proposition 3.12 through its use in Proposition 4.4. Recall Definition 2.8 for the definition of
![]() ${\mathcal {F}}$
, and also recall that
${\mathcal {F}}$
, and also recall that
![]() $\mathbb {P}$
denotes the Levy collapse poset
$\mathbb {P}$
denotes the Levy collapse poset
![]() $\operatorname {Col}(\omega _1,<\kappa )$
, where
$\operatorname {Col}(\omega _1,<\kappa )$
, where
![]() $\kappa $
is either ineffable or weakly compact. Two main ideas come into play in this section. The first is an axiomatization of various properties of the iterated club-adding
$\kappa $
is either ineffable or weakly compact. Two main ideas come into play in this section. The first is an axiomatization of various properties of the iterated club-adding
![]() $\dot {\mathbb {C}}_{\text {Magidor}}$
from [Reference Magidor31], which will allow us to place upper bounds on various “local” filters added by the Levy collapse. We then couple this axiomatization with a generalization of a result of Abraham [Reference Abraham1] that, in current language, if
$\dot {\mathbb {C}}_{\text {Magidor}}$
from [Reference Magidor31], which will allow us to place upper bounds on various “local” filters added by the Levy collapse. We then couple this axiomatization with a generalization of a result of Abraham [Reference Abraham1] that, in current language, if
![]() $\dot {\mathbb {Q}}$
is an
$\dot {\mathbb {Q}}$
is an
![]() $\operatorname {Add}(\omega ,\omega _1)$
-name for an
$\operatorname {Add}(\omega ,\omega _1)$
-name for an
![]() $\omega _1$
-closed poset, then
$\omega _1$
-closed poset, then
![]() $\operatorname {Add}(\omega ,\omega _1)\ast \dot {\mathbb {Q}}$
is strongly proper (see [Reference Gilton and Neeman15] for a proof of this fact as stated here). The strong properness results from using so-called “guiding reals.”
$\operatorname {Add}(\omega ,\omega _1)\ast \dot {\mathbb {Q}}$
is strongly proper (see [Reference Gilton and Neeman15] for a proof of this fact as stated here). The strong properness results from using so-called “guiding reals.”
We recall that in [Reference Magidor31], to show that an iteration
![]() $\dot {\mathbb {C}}_{\text {Magidor}}$
of length
$\dot {\mathbb {C}}_{\text {Magidor}}$
of length
![]() $<\kappa ^+$
adding the desired clubs is
$<\kappa ^+$
adding the desired clubs is
![]() $\kappa $
-distributive, Magidor argued, in part, as follows: let
$\kappa $
-distributive, Magidor argued, in part, as follows: let
![]() $j:M\longrightarrow N$
be a weakly compact embedding, where M has the relevant parameters. Let
$j:M\longrightarrow N$
be a weakly compact embedding, where M has the relevant parameters. Let
![]() $G^*$
be N-generic over
$G^*$
be N-generic over
![]() $j(\mathbb {P})$
and
$j(\mathbb {P})$
and
![]() $G:=G^*\cap \mathbb {P}$
, so that in
$G:=G^*\cap \mathbb {P}$
, so that in
![]() $N[G^*]$
, we may construct an
$N[G^*]$
, we may construct an
![]() $M[G]$
-generic filter H for
$M[G]$
-generic filter H for
![]() $\mathbb {C}_{\text {Magidor}}$
. Moreover,
$\mathbb {C}_{\text {Magidor}}$
. Moreover,
![]() $j[H]$
has a least upper bound in
$j[H]$
has a least upper bound in
![]() $j(\mathbb {C}_{\text {Magidor}})$
, namely, the function obtained by placing
$j(\mathbb {C}_{\text {Magidor}})$
, namely, the function obtained by placing
![]() $\kappa $
on top of each coordinate in the domain of
$\kappa $
on top of each coordinate in the domain of
![]() $j[H]$
; by the closure of the quotient (which implies the preservation of the stationary sets appearing along the way in the definition of
$j[H]$
; by the closure of the quotient (which implies the preservation of the stationary sets appearing along the way in the definition of
![]() $\mathbb {C}_{\text {Magidor}}$
), this is indeed a condition.
$\mathbb {C}_{\text {Magidor}}$
), this is indeed a condition.
The property of
![]() $\dot {\mathbb {C}}_{\text {Magidor}}$
which we will axiomatize is a reflection of the above to an
$\dot {\mathbb {C}}_{\text {Magidor}}$
which we will axiomatize is a reflection of the above to an
![]() $\mathcal {F}$
-positive set of
$\mathcal {F}$
-positive set of
![]() $\alpha <\kappa $
. Roughly, we want to say that for many
$\alpha <\kappa $
. Roughly, we want to say that for many
![]() $\alpha $
, if you “cut off”
$\alpha $
, if you “cut off”
![]() $\mathbb {P}\ast \dot {\mathbb {C}}$
at
$\mathbb {P}\ast \dot {\mathbb {C}}$
at
![]() $\alpha $
, then many generics added by the tail of the collapse for “
$\alpha $
, then many generics added by the tail of the collapse for “
![]() $\dot {\mathbb {C}}$
cut off at
$\dot {\mathbb {C}}$
cut off at
![]() $\alpha $
” have upper bounds in the full poset
$\alpha $
” have upper bounds in the full poset
![]() $\dot {\mathbb {C}}$
. More precisely, given a
$\dot {\mathbb {C}}$
. More precisely, given a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {\mathbb {C}}$
in
$\dot {\mathbb {C}}$
in
![]() $H(\kappa ^+)$
for a poset which is
$H(\kappa ^+)$
for a poset which is
![]() $\omega _1$
-closed with sups and given a
$\omega _1$
-closed with sups and given a
![]() $\dot {\mathbb {C}}$
-suitable model (see Definition 2.7) M, say with
$\dot {\mathbb {C}}$
-suitable model (see Definition 2.7) M, say with
![]() $M\cap \kappa =\alpha <\kappa $
, we consider the poset
$M\cap \kappa =\alpha <\kappa $
, we consider the poset
![]() $\pi _M(\dot {\mathbb {C}})$
, where
$\pi _M(\dot {\mathbb {C}})$
, where
![]() $\pi _M$
denotes the transitive collapse of M to
$\pi _M$
denotes the transitive collapse of M to
![]() $\bar {M}$
. An easy absoluteness argument shows that
$\bar {M}$
. An easy absoluteness argument shows that
![]() $\pi _M(\dot {\mathbb {C}})$
is a name in
$\pi _M(\dot {\mathbb {C}})$
is a name in
![]() $\pi _M(\mathbb {P})=\mathbb {P}\upharpoonright \alpha $
. Appealing to the closure of
$\pi _M(\mathbb {P})=\mathbb {P}\upharpoonright \alpha $
. Appealing to the closure of
![]() $\bar {M}$
under
$\bar {M}$
under
![]() $< \alpha $
-sequences, and hence
$< \alpha $
-sequences, and hence
![]() $\omega $
-sequences, we see that
$\omega $
-sequences, we see that
![]() $\pi _M(\dot {\mathbb {C}})$
is forced by
$\pi _M(\dot {\mathbb {C}})$
is forced by
![]() $\mathbb {P}\upharpoonright \alpha $
to be
$\mathbb {P}\upharpoonright \alpha $
to be
![]() $\omega _1$
-closed with sups. The desired condition on
$\omega _1$
-closed with sups. The desired condition on
![]() $\mathbb {P}$
-names
$\mathbb {P}$
-names
![]() $\dot {\mathbb {C}}$
can now be stated a bit more precisely: we will demand that after forcing with
$\dot {\mathbb {C}}$
can now be stated a bit more precisely: we will demand that after forcing with
![]() $\mathbb {P}$
, say to add the generic G, for many
$\mathbb {P}$
, say to add the generic G, for many
![]() $\alpha $
as above and many
$\alpha $
as above and many
![]() $V[G_{\mathbb {P}\upharpoonright \alpha }]$
-generics H for
$V[G_{\mathbb {P}\upharpoonright \alpha }]$
-generics H for
![]() $\pi _M(\dot {\mathbb {C}})[G_{\mathbb {P}\upharpoonright \alpha }]$
in
$\pi _M(\dot {\mathbb {C}})[G_{\mathbb {P}\upharpoonright \alpha }]$
in
![]() $V[G]$
,
$V[G]$
,
![]() $\pi ^{-1}_{M[G]}[H]$
has an upper bound in
$\pi ^{-1}_{M[G]}[H]$
has an upper bound in
![]() $\dot {\mathbb {C}}[G]$
. Note that we are implicitly appealing to the properness of
$\dot {\mathbb {C}}[G]$
. Note that we are implicitly appealing to the properness of
![]() $\mathbb {P}$
with respect to M to see that
$\mathbb {P}$
with respect to M to see that
![]() $\pi _M:M\longrightarrow \bar {M}$
lifts to
$\pi _M:M\longrightarrow \bar {M}$
lifts to
![]() $\pi _{M[G]}:M[G]\longrightarrow \bar {M}[G_{\mathbb {P}\upharpoonright \alpha }]$
; we discuss this more later.
$\pi _{M[G]}:M[G]\longrightarrow \bar {M}[G_{\mathbb {P}\upharpoonright \alpha }]$
; we discuss this more later.
The first step to making this work is to isolate exactly which filters we will use; for reasons related to building strong, exact residue functions later, we will not consider all filters added by the tail of the collapse for
![]() $\pi _M(\dot {\mathbb {C}})$
. The definition is meant to capture the behavior of filters generated by using the generic surjections to guide choices of conditions, similar to how Abraham used guiding reals in [Reference Abraham1].
$\pi _M(\dot {\mathbb {C}})$
. The definition is meant to capture the behavior of filters generated by using the generic surjections to guide choices of conditions, similar to how Abraham used guiding reals in [Reference Abraham1].
5.1 Residue functions from local filters
Definition 5.1 Let
![]() $\alpha <\kappa $
be inaccessible, and let
$\alpha <\kappa $
be inaccessible, and let
![]() $\dot {\mathbb {Q}}$
be a
$\dot {\mathbb {Q}}$
be a
![]() $(\mathbb {P}\upharpoonright \alpha )$
-name for a poset of size
$(\mathbb {P}\upharpoonright \alpha )$
-name for a poset of size
![]() $\alpha $
which is
$\alpha $
which is
![]() $\omega _1$
-closed with sups. Since
$\omega _1$
-closed with sups. Since
![]() $\mathbb {P}\upharpoonright \alpha $
is
$\mathbb {P}\upharpoonright \alpha $
is
![]() $\alpha $
-c.c., there exists a list
$\alpha $
-c.c., there exists a list
![]() ${\langle \dot {\gamma }_i:i<\alpha \rangle }$
of
${\langle \dot {\gamma }_i:i<\alpha \rangle }$
of
![]() $(\mathbb {P}\upharpoonright \alpha )$
-names, which is forced to enumerate all conditions in
$(\mathbb {P}\upharpoonright \alpha )$
-names, which is forced to enumerate all conditions in
![]() $\dot {\mathbb {Q}}$
. We say that a sequence
$\dot {\mathbb {Q}}$
. We say that a sequence
![]() $\dot {s}=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
of
$\dot {s}=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
of
![]() $\mathbb {P}$
-names (not
$\mathbb {P}$
-names (not
![]() $(\mathbb {P}\upharpoonright \alpha )$
-names) for conditions in
$(\mathbb {P}\upharpoonright \alpha )$
-names) for conditions in
![]() $\dot {\mathbb {Q}}$
is guided by the collapse at
$\dot {\mathbb {Q}}$
is guided by the collapse at
![]() $\alpha $
for
$\alpha $
for
![]() $\dot {\mathbb {Q}}$
if the following conditions are satisfied:
$\dot {\mathbb {Q}}$
if the following conditions are satisfied:
-
(1)
 $\Vdash _{\mathbb {P}}\langle \dot {d}_\nu :\nu <\omega _1\rangle $
is
$\Vdash _{\mathbb {P}}\langle \dot {d}_\nu :\nu <\omega _1\rangle $
is
 $\leq _{\dot {\mathbb {Q}}}$
-increasing,
$\leq _{\dot {\mathbb {Q}}}$
-increasing,
 $\dot {d}_0$
is the weakest condition in
$\dot {d}_0$
is the weakest condition in
 $\dot {\mathbb {Q}}$
, and if
$\dot {\mathbb {Q}}$
, and if
 $\nu $
is limit, then
$\nu $
is limit, then
 $\dot {d}_\nu $
is a sup of
$\dot {d}_\nu $
is a sup of
 $\langle \dot {d}_\mu :\mu <\nu \rangle $
.
$\langle \dot {d}_\mu :\mu <\nu \rangle $
. -
(2) If
 $p\in \mathbb {P}$
and
$p\in \mathbb {P}$
and
 $\operatorname {dom}(p(\alpha ))$
is an ordinal
$\operatorname {dom}(p(\alpha ))$
is an ordinal
 $\nu <\omega _1$
, then there exists
$\nu <\omega _1$
, then there exists
 $p'\geq p$
with
$p'\geq p$
with
 $p'\upharpoonright [\alpha ,\kappa )=p\upharpoonright [\alpha ,\kappa )$
and a sequence
$p'\upharpoonright [\alpha ,\kappa )=p\upharpoonright [\alpha ,\kappa )$
and a sequence
 $\langle \beta (\mu ):\mu \leq \nu \rangle $
of ordinals in V so that
$\langle \beta (\mu ):\mu \leq \nu \rangle $
of ordinals in V so that
 $p'\Vdash \dot {d}_\mu =^*\dot {\gamma }_{\beta (\mu )}$
for all
$p'\Vdash \dot {d}_\mu =^*\dot {\gamma }_{\beta (\mu )}$
for all
 $\mu \leq \nu $
. In this case, we will say that
$\mu \leq \nu $
. In this case, we will say that
 $p'$
determines an initial segment of
$p'$
determines an initial segment of
 $\dot {s}$
.
$\dot {s}$
. -
(3) If
 $p'$
as in (2) determines an initial segment of
$p'$
as in (2) determines an initial segment of
 $\dot {s}$
and if
$\dot {s}$
and if
 $\dot {\gamma }$
is a
$\dot {\gamma }$
is a
 $(\mathbb {P}\upharpoonright \alpha )$
-name for a
$(\mathbb {P}\upharpoonright \alpha )$
-name for a
 $\dot {\mathbb {Q}}$
-extension of
$\dot {\mathbb {Q}}$
-extension of
 $\dot {\gamma }_{\beta (\nu )}$
, then there exists
$\dot {\gamma }_{\beta (\nu )}$
, then there exists
 $p^*\geq p'$
so that
$p^*\geq p'$
so that
 $p^*\Vdash \dot {d}_{\nu +1}\geq \dot {\gamma }$
.
$p^*\Vdash \dot {d}_{\nu +1}\geq \dot {\gamma }$
.
Lemma 5.1 Suppose that
![]() $\dot {s}:=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
is guided by the collapse at
$\dot {s}:=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
is guided by the collapse at
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $H(\dot {s})$
be the
$H(\dot {s})$
be the
![]() $\mathbb {P}$
-name for the filter on
$\mathbb {P}$
-name for the filter on
![]() $\dot {\mathbb {Q}}$
generated by
$\dot {\mathbb {Q}}$
generated by
![]() $\dot {s}$
. Then
$\dot {s}$
. Then
![]() $\mathbb {P}$
forces that
$\mathbb {P}$
forces that
![]() $H(\dot {s})$
is
$H(\dot {s})$
is
![]() $V[\dot {G}\upharpoonright \alpha ]$
-generic over
$V[\dot {G}\upharpoonright \alpha ]$
-generic over
![]() $\dot {\mathbb {Q}}$
.
$\dot {\mathbb {Q}}$
.
Proof Fix a condition
![]() $p\in \mathbb {P}$
and a
$p\in \mathbb {P}$
and a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {D}$
for a dense subset of
$\dot {D}$
for a dense subset of
![]() $\dot {\mathbb {Q}}$
which is a member of
$\dot {\mathbb {Q}}$
which is a member of
![]() $V[\dot {G}\upharpoonright \alpha ]$
. We find an extension of p which forces that
$V[\dot {G}\upharpoonright \alpha ]$
. We find an extension of p which forces that
![]() $\dot {D}\cap H(\dot {s})\neq \emptyset $
. By extending p and applying (2) of Definition 5.1 if necessary, we may assume the following:
$\dot {D}\cap H(\dot {s})\neq \emptyset $
. By extending p and applying (2) of Definition 5.1 if necessary, we may assume the following:
-
(1) there is a
 $(\mathbb {P}\upharpoonright \alpha )$
-name
$(\mathbb {P}\upharpoonright \alpha )$
-name
 $\dot {D}_0$
for a dense subset of
$\dot {D}_0$
for a dense subset of
 $\dot {\mathbb {Q}}$
so that
$\dot {\mathbb {Q}}$
so that
 $p\Vdash \dot {D}=\dot {D}_0$
; and
$p\Vdash \dot {D}=\dot {D}_0$
; and -
(2)
 $\operatorname {dom}(p(\alpha ))$
is an ordinal
$\operatorname {dom}(p(\alpha ))$
is an ordinal
 $\nu $
, and there is a sequence
$\nu $
, and there is a sequence
 $\langle \beta (\mu ):\mu \leq \nu \rangle $
of ordinals in V so that
$\langle \beta (\mu ):\mu \leq \nu \rangle $
of ordinals in V so that
 $p\Vdash \dot {d}_\mu =^*\dot {\gamma }_{\beta (\mu )}$
for all
$p\Vdash \dot {d}_\mu =^*\dot {\gamma }_{\beta (\mu )}$
for all
 $\mu \leq \nu $
.
$\mu \leq \nu $
.
Let
![]() $\dot {\gamma }$
be a
$\dot {\gamma }$
be a
![]() $(\mathbb {P}\upharpoonright \alpha )$
-name for a condition in
$(\mathbb {P}\upharpoonright \alpha )$
-name for a condition in
![]() $\dot {D}_0$
forced to extend
$\dot {D}_0$
forced to extend
![]() $\dot {\gamma }_{\beta (\nu )}$
. By item (3) of Definition 5.1, we may find an extension
$\dot {\gamma }_{\beta (\nu )}$
. By item (3) of Definition 5.1, we may find an extension
![]() $p^*$
of p so that
$p^*$
of p so that
![]() $p^*\Vdash \dot {d}_{\nu +1}\geq \dot {\gamma }$
. Then
$p^*\Vdash \dot {d}_{\nu +1}\geq \dot {\gamma }$
. Then
![]() $p^*\Vdash \dot {\gamma }\in \dot {D}\cap H(\dot {s})$
, finishing the proof.▪
$p^*\Vdash \dot {\gamma }\in \dot {D}\cap H(\dot {s})$
, finishing the proof.▪
Definition 5.2 Let
![]() $\dot {H}$
be a
$\dot {H}$
be a
![]() $\mathbb {P}$
-name for a filter on
$\mathbb {P}$
-name for a filter on
![]() $\dot {\mathbb {Q}}$
. We say that
$\dot {\mathbb {Q}}$
. We say that
![]() $\dot {H}$
is guided by the collapse at
$\dot {H}$
is guided by the collapse at
![]() $\alpha $
if there is a sequence
$\alpha $
if there is a sequence
![]() $\dot {s}=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
of conditions guided by the collapse at
$\dot {s}=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
of conditions guided by the collapse at
![]() $\alpha $
so that
$\alpha $
so that
![]() $\dot {H}=H(\dot {s})$
.
$\dot {H}=H(\dot {s})$
.
Suppose that M is a suitable model. Let
![]() $\alpha :=M\cap \kappa $
, and let
$\alpha :=M\cap \kappa $
, and let
![]() $\pi _M: M \to \bar {M}$
be the transitive collapse map of M. Let
$\pi _M: M \to \bar {M}$
be the transitive collapse map of M. Let
![]() $G \subseteq \mathbb {P}$
be generic over V, and set
$G \subseteq \mathbb {P}$
be generic over V, and set
![]() $G_\alpha = G \cap (\mathbb {P}\upharpoonright \alpha )$
. We have that
$G_\alpha = G \cap (\mathbb {P}\upharpoonright \alpha )$
. We have that
![]() $\mathbb {P}\upharpoonright \alpha = \pi _M(\mathbb {P}) \in \bar {M}$
, and
$\mathbb {P}\upharpoonright \alpha = \pi _M(\mathbb {P}) \in \bar {M}$
, and
![]() $G_\alpha \subset \pi _M(\mathbb {P})$
is generic for
$G_\alpha \subset \pi _M(\mathbb {P})$
is generic for
![]() $\bar {M}$
. Moreover, setting
$\bar {M}$
. Moreover, setting
![]() $M[G] = \{ \dot {x}[G] \mid \dot {x} \in M \text { is a }{\mathbb {P}}\text {-name}\}$
, we have that
$M[G] = \{ \dot {x}[G] \mid \dot {x} \in M \text { is a }{\mathbb {P}}\text {-name}\}$
, we have that
![]() $\bar {M}[G_\alpha ]$
is the transitive collapse of
$\bar {M}[G_\alpha ]$
is the transitive collapse of
![]() $M[G]$
, with the transitive collapse map
$M[G]$
, with the transitive collapse map
![]() $\pi _{M[G]}$
being the natural extension of
$\pi _{M[G]}$
being the natural extension of
![]() $\pi _M$
, given by
$\pi _M$
, given by
![]() $\pi _{M[G]}(\dot {x}[G]) = \pi _M(\dot {x})[G_\alpha ]$
.
$\pi _{M[G]}(\dot {x}[G]) = \pi _M(\dot {x})[G_\alpha ]$
.
Lemma 5.2 Suppose that M is a
![]() $(\mathbb {P}\ast \dot {\mathbb {C}})$
-suitable model, where
$(\mathbb {P}\ast \dot {\mathbb {C}})$
-suitable model, where
![]() $\dot {\mathbb {C}}$
is a
$\dot {\mathbb {C}}$
is a
![]() $\mathbb {P}$
-name for a poset on
$\mathbb {P}$
-name for a poset on
![]() $\kappa $
which is
$\kappa $
which is
![]() $\omega _1$
-closed with sups. Let
$\omega _1$
-closed with sups. Let
![]() $\alpha :=M\cap \kappa $
and
$\alpha :=M\cap \kappa $
and
![]() $\pi _{M}$
be the transitive collapse map of M. Suppose that
$\pi _{M}$
be the transitive collapse map of M. Suppose that
![]() $\dot {H}$
is a
$\dot {H}$
is a
![]() $\mathbb {P}$
-name for a subset of
$\mathbb {P}$
-name for a subset of
![]() $\pi _M(\dot {\mathbb {C}})$
which is guided by the collapse at
$\pi _M(\dot {\mathbb {C}})$
which is guided by the collapse at
![]() $\alpha $
for
$\alpha $
for
![]() $\pi _M(\dot {\mathbb {C}})$
, and further suppose that there is a
$\pi _M(\dot {\mathbb {C}})$
, and further suppose that there is a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {c}$
for a condition in
$\dot {c}$
for a condition in
![]() $\dot {\mathbb {C}}$
which is forced to be an upper bound for
$\dot {\mathbb {C}}$
which is forced to be an upper bound for
![]() $\pi ^{-1}_{M[\dot {G}]}[\dot {H}]$
. Then
$\pi ^{-1}_{M[\dot {G}]}[\dot {H}]$
. Then
![]() $\mathbb {P}$
forces that
$\mathbb {P}$
forces that
![]() $\dot {c}$
is an
$\dot {c}$
is an
![]() $(M[\dot {G}],\dot {\mathbb {C}})$
-completely generic condition.
$(M[\dot {G}],\dot {\mathbb {C}})$
-completely generic condition.
Proof Fix G. To see that
![]() $c = {\dot {c}[G]}$
is
$c = {\dot {c}[G]}$
is
![]() $(M[G],\mathbb {C})$
-completely generic, fix a dense, open
$(M[G],\mathbb {C})$
-completely generic, fix a dense, open
![]() $E\subseteq \mathbb {C}$
with
$E\subseteq \mathbb {C}$
with
![]() $E\in M[G]$
. We show that c extends some condition in E.
$E\in M[G]$
. We show that c extends some condition in E.
By the elementarity of
![]() $\pi _{M[G]} : M[G] \to \bar {M}[G_\alpha ]$
, we know that
$\pi _{M[G]} : M[G] \to \bar {M}[G_\alpha ]$
, we know that
![]() $\pi _{M[G]}(E)$
is dense in
$\pi _{M[G]}(E)$
is dense in
![]() $\pi _{M[G]}(\mathbb {C})=\pi _M(\dot {\mathbb {C}})[G_\alpha ]$
. Since
$\pi _{M[G]}(\mathbb {C})=\pi _M(\dot {\mathbb {C}})[G_\alpha ]$
. Since
![]() $H:=\dot {H}[G]$
is a
$H:=\dot {H}[G]$
is a
![]() $V[{G_\alpha }]$
-generic filter, by Lemma 5.1,
$V[{G_\alpha }]$
-generic filter, by Lemma 5.1,
![]() $H\cap \pi _{M[G]}(E)\neq \emptyset $
, and thus
$H\cap \pi _{M[G]}(E)\neq \emptyset $
, and thus
![]() $\pi ^{-1}_{M[G]}[H] \cap E \neq \emptyset $
.▪
$\pi ^{-1}_{M[G]}[H] \cap E \neq \emptyset $
.▪
There are two particularly useful properties of this class of names for generic filters. On the one hand, filters in this class will allow us to generate strong, exact residue functions by isolating the information which a given conditions determines about the filters. On the other hand, the class of such filters for one poset, such as a two-step iteration, often projects to the class of such filters for another poset, such as the first step in a two-step iteration. This property will be particularly useful in Section 6 when we want to show, by induction, that our club-adding poset is well behaved.
It is straightforward to verify that the notion of
![]() $\mathbb {P}$
-names of filters, which are guided by the collapse at a given cardinal, factor well in iterations.
$\mathbb {P}$
-names of filters, which are guided by the collapse at a given cardinal, factor well in iterations.
Lemma 5.3 Suppose that
![]() $\alpha <\kappa $
is inaccessible and that
$\alpha <\kappa $
is inaccessible and that
![]() $\dot {\mathbb {Q}_0}\ast \dot {\mathbb {Q}}_1$
is a
$\dot {\mathbb {Q}_0}\ast \dot {\mathbb {Q}}_1$
is a
![]() $(\mathbb {P}\upharpoonright \alpha )$
-name for a two-step poset of size
$(\mathbb {P}\upharpoonright \alpha )$
-name for a two-step poset of size
![]() $\alpha $
which is
$\alpha $
which is
![]() $\omega _1$
-closed with sups. Let
$\omega _1$
-closed with sups. Let
![]() $\langle \dot {d}_\nu :\nu <\omega _1\rangle $
be a sequence of
$\langle \dot {d}_\nu :\nu <\omega _1\rangle $
be a sequence of
![]() $\mathbb {P}$
-names which is guided by the collapse at
$\mathbb {P}$
-names which is guided by the collapse at
![]() $\alpha $
for
$\alpha $
for
![]() $\dot {\mathbb {Q}}_0\ast \dot {\mathbb {Q}}_1$
. Then the sequence
$\dot {\mathbb {Q}}_0\ast \dot {\mathbb {Q}}_1$
. Then the sequence
![]() $\langle \dot {d}_\nu (0):\nu <\omega _1\rangle $
of
$\langle \dot {d}_\nu (0):\nu <\omega _1\rangle $
of
![]() $\mathbb {P}$
-names of conditions in
$\mathbb {P}$
-names of conditions in
![]() $\dot {\mathbb {Q}}_0$
is guided by the collapse at
$\dot {\mathbb {Q}}_0$
is guided by the collapse at
![]() $\alpha $
for
$\alpha $
for
![]() $\dot {\mathbb {Q}}_0$
.
$\dot {\mathbb {Q}}_0$
.
The following proposition shows how to generate exact, strong residue functions from the filters discussed above.
Proposition 5.4 Suppose that
![]() $\dot {\mathbb {C}}$
is a
$\dot {\mathbb {C}}$
is a
![]() $\mathbb {P}$
-name in
$\mathbb {P}$
-name in
![]() $H(\kappa ^+)$
for a poset of size
$H(\kappa ^+)$
for a poset of size
![]() $\kappa $
which is
$\kappa $
which is
![]() $\omega _1$
-closed with sups, and set
$\omega _1$
-closed with sups, and set
![]() $\mathbb {P}^*:=\mathbb {P}\ast \dot {\mathbb {C}}$
. Let M be a
$\mathbb {P}^*:=\mathbb {P}\ast \dot {\mathbb {C}}$
. Let M be a
![]() $(\mathbb {P}\ast \dot {\mathbb {C}})$
-suitable model, say with
$(\mathbb {P}\ast \dot {\mathbb {C}})$
-suitable model, say with
![]() $\alpha :=M\cap \kappa <\kappa $
, and let
$\alpha :=M\cap \kappa <\kappa $
, and let
![]() $\pi _M$
denote the transitive collapse of M. Furthermore, let
$\pi _M$
denote the transitive collapse of M. Furthermore, let
![]() $\dot {s}=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
be a sequence of
$\dot {s}=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
be a sequence of
![]() $\mathbb {P}$
-names guided by the collapse at
$\mathbb {P}$
-names guided by the collapse at
![]() $\alpha $
for
$\alpha $
for
![]() $\pi _M(\dot {\mathbb {C}})$
. In addition, suppose that there is a
$\pi _M(\dot {\mathbb {C}})$
. In addition, suppose that there is a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {d}^*$
for a condition in
$\dot {d}^*$
for a condition in
![]() $\dot {\mathbb {C}}$
which is forced to be an upper bound for the sequence
$\dot {\mathbb {C}}$
which is forced to be an upper bound for the sequence
![]() $\pi _{M[\dot {G}]}^{-1}[\dot {s}]$
.
$\pi _{M[\dot {G}]}^{-1}[\dot {s}]$
.
Define
![]() $p^*(M)$
to be the condition
$p^*(M)$
to be the condition
and let
Finally, define
![]() $\varphi ^M$
on
$\varphi ^M$
on
![]() $D(M)$
by
$D(M)$
by
where
![]() $\beta <\alpha $
is the least so that
$\beta <\alpha $
is the least so that
![]() $p\Vdash \dot {d}_{\operatorname {dom}(p(\alpha ))}=^*\dot {\gamma }_\beta $
(
$p\Vdash \dot {d}_{\operatorname {dom}(p(\alpha ))}=^*\dot {\gamma }_\beta $
(
![]() $\beta $
exists by definition of “p determines an initial segment of
$\beta $
exists by definition of “p determines an initial segment of
![]() $\dot {s}$
”). Then:
$\dot {s}$
”). Then:
-
(a)
 $D(M)$
is a dense, countably
$D(M)$
is a dense, countably
 $=^*$
-closed subset of
$=^*$
-closed subset of
 $\mathbb {P}^*/p^*(M)$
;
$\mathbb {P}^*/p^*(M)$
; -
(b)
 $p^*(M)$
is compatible with every condition in
$p^*(M)$
is compatible with every condition in
 $\mathbb {P}^*\cap M$
; and
$\mathbb {P}^*\cap M$
; and -
(c)
 $\varphi ^M$
is an exact, strong residue function from
$\varphi ^M$
is an exact, strong residue function from
 $D(M)$
to
$D(M)$
to
 $M\cap \mathbb {P}^*$
.
$M\cap \mathbb {P}^*$
.
Proof Let
![]() $\langle \dot {\gamma }_i:i<\alpha \rangle $
be a sequence of
$\langle \dot {\gamma }_i:i<\alpha \rangle $
be a sequence of
![]() $(\mathbb {P}\upharpoonright \alpha )$
-names which is forced to enumerate all conditions in
$(\mathbb {P}\upharpoonright \alpha )$
-names which is forced to enumerate all conditions in
![]() $\pi _M(\dot {\mathbb {C}})$
, and with
$\pi _M(\dot {\mathbb {C}})$
, and with
![]() $\dot {d}^*$
, satisfies Definition 5.1, witnessing that
$\dot {d}^*$
, satisfies Definition 5.1, witnessing that
![]() $\dot {s}=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
is guided by the collapse at
$\dot {s}=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
is guided by the collapse at
![]() $\alpha $
for
$\alpha $
for
![]() $\pi _M(\dot {\mathbb {C}})$
.
$\pi _M(\dot {\mathbb {C}})$
.
We first prove item (a). Given a condition
![]() $(p,\dot {d})$
in
$(p,\dot {d})$
in
![]() $\mathbb {P}^*/p^*(M)$
, by item (2) of Definition 5.1, we may find an extension
$\mathbb {P}^*/p^*(M)$
, by item (2) of Definition 5.1, we may find an extension
![]() $p'$
of p so that p determines an initial segment of
$p'$
of p so that p determines an initial segment of
![]() $\dot {s}$
. Then
$\dot {s}$
. Then
![]() $(p',\dot {d})\geq (p,\dot {d})$
is in
$(p',\dot {d})\geq (p,\dot {d})$
is in
![]() $D(M)$
, proving density. Similarly,
$D(M)$
, proving density. Similarly,
![]() $D(M)$
is
$D(M)$
is
![]() $=^*$
-closed: if
$=^*$
-closed: if
![]() $(p_1,\dot {d}_1)\in D(M)$
and
$(p_1,\dot {d}_1)\in D(M)$
and
![]() $(p_1,\dot {d}_1)=^*(p_2,\dot {d}_2)$
, then
$(p_1,\dot {d}_1)=^*(p_2,\dot {d}_2)$
, then
![]() $p_2$
determines an initial segment of
$p_2$
determines an initial segment of
![]() $\dot {s}$
, because
$\dot {s}$
, because
![]() $p_2=p_1$
(recall these are collapse conditions) and because
$p_2=p_1$
(recall these are collapse conditions) and because
![]() $(p_2,\dot {d}_2)\geq (p_1,\dot {d}_1)\geq (0_{\mathbb {P}},\dot {d}^*)$
.
$(p_2,\dot {d}_2)\geq (p_1,\dot {d}_1)\geq (0_{\mathbb {P}},\dot {d}^*)$
.
To see that
![]() $D(M)$
is closed under sups of increasing
$D(M)$
is closed under sups of increasing
![]() $\omega $
-sequences, suppose that
$\omega $
-sequences, suppose that
![]() $\langle (p_n,\dot {c}_n):n\in \omega \rangle $
is an increasing sequence of conditions in
$\langle (p_n,\dot {c}_n):n\in \omega \rangle $
is an increasing sequence of conditions in
![]() $D(M)$
, and let
$D(M)$
, and let
![]() $(p^*,\dot {c}^*)$
be a sup. Set
$(p^*,\dot {c}^*)$
be a sup. Set
![]() $\nu _n:=\operatorname {dom}(p_n(\alpha ))$
and
$\nu _n:=\operatorname {dom}(p_n(\alpha ))$
and
![]() $\nu ^*:=\operatorname {dom}(p^*(\alpha ))$
. If
$\nu ^*:=\operatorname {dom}(p^*(\alpha ))$
. If
![]() $\nu ^*=\nu _m$
for some
$\nu ^*=\nu _m$
for some
![]() $m\in \omega $
, then because
$m\in \omega $
, then because
![]() $p_m$
determines
$p_m$
determines
![]() $\dot {s}$
up to
$\dot {s}$
up to
![]() $\nu _m$
, we have that
$\nu _m$
, we have that
![]() $p^*$
determines
$p^*$
determines
![]() $\dot {s}$
up to
$\dot {s}$
up to
![]() $\nu ^*=\nu _m$
. Thus,
$\nu ^*=\nu _m$
. Thus,
![]() $p^*$
determines an initial segment of
$p^*$
determines an initial segment of
![]() $\dot {s}$
in this case. So consider the case that
$\dot {s}$
in this case. So consider the case that
![]() $\nu ^*>\nu _m$
for all m; in particular,
$\nu ^*>\nu _m$
for all m; in particular,
![]() $\nu ^*$
is a limit ordinal. Since for all
$\nu ^*$
is a limit ordinal. Since for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $p_n$
determines an initial segment of
$p_n$
determines an initial segment of
![]() $\dot {s}$
and
$\dot {s}$
and
![]() $p^*\geq p_n$
, we may find a sequence
$p^*\geq p_n$
, we may find a sequence
![]() $\langle \beta (\mu ):\mu <\nu ^*\rangle $
in V so that
$\langle \beta (\mu ):\mu <\nu ^*\rangle $
in V so that
![]() $p^*\Vdash \dot {d}_\mu =^*\dot {\gamma }_{\beta (\mu )}$
for all
$p^*\Vdash \dot {d}_\mu =^*\dot {\gamma }_{\beta (\mu )}$
for all
![]() $\mu <\nu ^*$
. Now, let
$\mu <\nu ^*$
. Now, let
![]() $\beta (\nu ^*)$
be chosen so that
$\beta (\nu ^*)$
be chosen so that
![]() $\dot {\gamma }_{\beta (\nu ^*)}$
is forced to be a sup of
$\dot {\gamma }_{\beta (\nu ^*)}$
is forced to be a sup of
![]() $\langle \dot {\gamma }_{\beta (\mu )}:\mu <\nu \rangle $
, if this sequence is increasing, and equals the trivial condition otherwise. Since
$\langle \dot {\gamma }_{\beta (\mu )}:\mu <\nu \rangle $
, if this sequence is increasing, and equals the trivial condition otherwise. Since
![]() $\nu ^*$
is a limit,
$\nu ^*$
is a limit,
![]() $\Vdash _{\mathbb {P}}\dot {d}_{\nu ^*}$
is a sup of
$\Vdash _{\mathbb {P}}\dot {d}_{\nu ^*}$
is a sup of
![]() $\langle \dot {d}_\mu :\mu <\nu ^*\rangle $
. However,
$\langle \dot {d}_\mu :\mu <\nu ^*\rangle $
. However,
![]() $p^*$
forces that
$p^*$
forces that
![]() $\dot {d}_\mu =^*\dot {\gamma }_{\beta (\mu )}$
for all
$\dot {d}_\mu =^*\dot {\gamma }_{\beta (\mu )}$
for all
![]() $\mu <\nu ^*$
, and therefore
$\mu <\nu ^*$
, and therefore
![]() $p^*$
forces that
$p^*$
forces that
![]() $\dot {d}_{\nu ^*}=^*\dot {\gamma }_{\beta (\nu ^*)}$
. Thus, in either case,
$\dot {d}_{\nu ^*}=^*\dot {\gamma }_{\beta (\nu ^*)}$
. Thus, in either case,
![]() $p^*$
determines an initial segment of
$p^*$
determines an initial segment of
![]() $\dot {s}$
, which finishes the proof of (a).
$\dot {s}$
, which finishes the proof of (a).
Now, we verify item (b). Fix a condition
![]() $(u,\dot {c}_0)$
in
$(u,\dot {c}_0)$
in
![]() $\mathbb {P}^*\cap M$
, and we will show that it is compatible with
$\mathbb {P}^*\cap M$
, and we will show that it is compatible with
![]() $p^*(M)$
. We observe that, trivially, u determines an initial segment of
$p^*(M)$
. We observe that, trivially, u determines an initial segment of
![]() $\dot {s}$
since
$\dot {s}$
since
![]() $\operatorname {dom}(u(\alpha ))=0$
and
$\operatorname {dom}(u(\alpha ))=0$
and
![]() $\Vdash _{\mathbb {P}}\dot {d}_0$
is the trivial condition in
$\Vdash _{\mathbb {P}}\dot {d}_0$
is the trivial condition in
![]() $\pi _M(\dot {\mathbb {C}})$
, by (1) of Definition 5.1. By (3) of the same definition, we may find an extension
$\pi _M(\dot {\mathbb {C}})$
, by (1) of Definition 5.1. By (3) of the same definition, we may find an extension
![]() $p\geq u$
s.t.
$p\geq u$
s.t.
![]() $p\Vdash \dot {d}_1\geq \pi _M(\dot {c}_0)$
. Then
$p\Vdash \dot {d}_1\geq \pi _M(\dot {c}_0)$
. Then
![]() $(p,\dot {d}^*)$
extends
$(p,\dot {d}^*)$
extends
![]() $(u,\dot {c}_0)$
since p forces that
$(u,\dot {c}_0)$
since p forces that
![]() $\dot {d}^*$
is an upper bound for the sequence
$\dot {d}^*$
is an upper bound for the sequence
![]() $\pi _M^{-1}[\dot {s}]$
and that
$\pi _M^{-1}[\dot {s}]$
and that
![]() $\pi ^{-1}_M(\dot {d}_1)\geq \dot {c}_0$
.
$\pi ^{-1}_M(\dot {d}_1)\geq \dot {c}_0$
.
It therefore remains to verify that
![]() $\varphi ^M$
is an exact, strong residue function. Condition (1) of Definition 2.5 holds since, by (a),
$\varphi ^M$
is an exact, strong residue function. Condition (1) of Definition 2.5 holds since, by (a),
![]() $D(M)$
is dense and countably
$D(M)$
is dense and countably
![]() $=^*$
-closed in
$=^*$
-closed in
![]() $\mathbb {P}^*/p^*(M)$
. For the projection condition of Definition 2.5, fix
$\mathbb {P}^*/p^*(M)$
. For the projection condition of Definition 2.5, fix
![]() $(p,\dot {c})\in D(M)$
, and let
$(p,\dot {c})\in D(M)$
, and let
![]() $\dot {\gamma }$
be the
$\dot {\gamma }$
be the
![]() $(\mathbb {P}\upharpoonright \alpha )$
-name so that
$(\mathbb {P}\upharpoonright \alpha )$
-name so that
![]() $\varphi ^M(p,\dot {c})=(p\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }))$
. Since
$\varphi ^M(p,\dot {c})=(p\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }))$
. Since
![]() $(p,\dot {c})\in D(M)$
, p determines an initial segment of
$(p,\dot {c})\in D(M)$
, p determines an initial segment of
![]() $\dot {s}$
, and therefore
$\dot {s}$
, and therefore
![]() $p\Vdash \dot {d}_{\operatorname {dom}(p(\alpha ))}=^*\dot {\gamma }$
. Since p also forces that
$p\Vdash \dot {d}_{\operatorname {dom}(p(\alpha ))}=^*\dot {\gamma }$
. Since p also forces that
![]() $\dot {c}\geq \dot {d}^*$
, p forces that
$\dot {c}\geq \dot {d}^*$
, p forces that
![]() $\dot {c}$
is an upper bound for
$\dot {c}$
is an upper bound for
![]() $\pi _M^{-1}[\dot {s}]$
and therefore that
$\pi _M^{-1}[\dot {s}]$
and therefore that
![]() $\dot {c}$
extends
$\dot {c}$
extends
![]() $\pi _M^{-1}(\dot {d}_{\operatorname {dom}(p(\alpha ))})=^*\pi _M^{-1}(\dot {\gamma })$
. Therefore,
$\pi _M^{-1}(\dot {d}_{\operatorname {dom}(p(\alpha ))})=^*\pi _M^{-1}(\dot {\gamma })$
. Therefore,
![]() $(p,\dot {c})\geq (p\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }))=\varphi ^M(p,\dot {c})$
.
$(p,\dot {c})\geq (p\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }))=\varphi ^M(p,\dot {c})$
.
It is straightforward to verify that
![]() $\varphi ^M$
is order preserving, i.e., condition (3) of Definition 2.5. So we prove that
$\varphi ^M$
is order preserving, i.e., condition (3) of Definition 2.5. So we prove that
![]() $\varphi ^M$
has the strong residue property (condition (4) of Definition 2.5). Thus, fix
$\varphi ^M$
has the strong residue property (condition (4) of Definition 2.5). Thus, fix
![]() $(p,\dot {c})\in D(M)$
, where we let
$(p,\dot {c})\in D(M)$
, where we let
![]() $\nu :=\operatorname {dom}(p(\alpha ))$
and
$\nu :=\operatorname {dom}(p(\alpha ))$
and
![]() $\dot {\gamma }$
so that
$\dot {\gamma }$
so that
![]() $\varphi ^M(p,\dot {c})=(p\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }))$
. Fix a condition
$\varphi ^M(p,\dot {c})=(p\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }))$
. Fix a condition
![]() $(u,\dot {\delta })$
in
$(u,\dot {\delta })$
in
![]() $\mathbb {P}^*\cap M$
with
$\mathbb {P}^*\cap M$
with
![]() $(u,\dot {\delta })\geq (p\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }))$
, and we will verify that
$(u,\dot {\delta })\geq (p\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }))$
, and we will verify that
![]() $(u,\dot {\delta })$
is compatible with
$(u,\dot {\delta })$
is compatible with
![]() $(p,\dot {c})$
. Let
$(p,\dot {c})$
. Let
![]() $p':=u\cup p$
, a condition in
$p':=u\cup p$
, a condition in
![]() $\mathbb {P}$
, and observe that
$\mathbb {P}$
, and observe that
![]() $p'$
still determines an initial segment of
$p'$
still determines an initial segment of
![]() $\dot {s}$
and
$\dot {s}$
and
![]() $\nu =\operatorname {dom}(p'(\alpha ))$
. By item (3) of Definition 5.1, we may find some
$\nu =\operatorname {dom}(p'(\alpha ))$
. By item (3) of Definition 5.1, we may find some
![]() $p^*\geq p'$
so that
$p^*\geq p'$
so that
![]() $p^*\Vdash \dot {d}_{\nu +1}\geq \pi _M(\dot {\delta })$
. Then
$p^*\Vdash \dot {d}_{\nu +1}\geq \pi _M(\dot {\delta })$
. Then
![]() $(p^*,\dot {c})$
extends both
$(p^*,\dot {c})$
extends both
![]() $(p,\dot {c})$
and
$(p,\dot {c})$
and
![]() $(u,\dot {\delta })$
.
$(u,\dot {\delta })$
.
We now check that
![]() $\varphi ^M$
is
$\varphi ^M$
is
![]() $\omega $
-continuous, which will finish the proof of (c) and thereby the proof of the proposition. Fix an increasing sequence of conditions
$\omega $
-continuous, which will finish the proof of (c) and thereby the proof of the proposition. Fix an increasing sequence of conditions
![]() $\langle (p_n,\dot {c}_n):n\in \omega \rangle $
in
$\langle (p_n,\dot {c}_n):n\in \omega \rangle $
in
![]() $D(M)$
, and let
$D(M)$
, and let
![]() $(p^*,\dot {c}^*)$
be a supremum of this sequence. Then
$(p^*,\dot {c}^*)$
be a supremum of this sequence. Then
![]() $p^*:=\bigcup _np_n$
, and
$p^*:=\bigcup _np_n$
, and
![]() $\dot {c}^*$
is forced by
$\dot {c}^*$
is forced by
![]() $p^*$
to be a sup of
$p^*$
to be a sup of
![]() $\langle \dot {c}_n:n\in \omega \rangle $
. By item (a) of the proposition,
$\langle \dot {c}_n:n\in \omega \rangle $
. By item (a) of the proposition,
![]() $(p^*,\dot {c}^*)\in D(M)$
. We need to show that
$(p^*,\dot {c}^*)\in D(M)$
. We need to show that
![]() $\varphi ^M(p^*,\dot {c}^*)$
is a sup of
$\varphi ^M(p^*,\dot {c}^*)$
is a sup of
![]() $\langle \varphi ^M(p_n,\dot {c}_n):n\in \omega \rangle $
. For each
$\langle \varphi ^M(p_n,\dot {c}_n):n\in \omega \rangle $
. For each
![]() $n<\omega $
, set
$n<\omega $
, set
![]() $\nu _n:=\operatorname {dom}(p_n(\alpha ))$
, and also set
$\nu _n:=\operatorname {dom}(p_n(\alpha ))$
, and also set
![]() $\nu ^*:=\operatorname {dom}(p^*(\alpha ))$
. In addition, for each n, fix the least ordinal
$\nu ^*:=\operatorname {dom}(p^*(\alpha ))$
. In addition, for each n, fix the least ordinal
![]() $\beta (\nu _n)$
with
$\beta (\nu _n)$
with
![]() $p_n\Vdash \dot {d}_{\nu _n}=^*\dot {\gamma }_{\beta (\nu _n)}$
, so that
$p_n\Vdash \dot {d}_{\nu _n}=^*\dot {\gamma }_{\beta (\nu _n)}$
, so that
![]() $\varphi ^M(p_n,\dot {c}_n)=(p_n\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }_{\beta (\nu _n)}))$
. Finally, let
$\varphi ^M(p_n,\dot {c}_n)=(p_n\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }_{\beta (\nu _n)}))$
. Finally, let
![]() $\beta (\nu ^*)$
be least so that
$\beta (\nu ^*)$
be least so that
![]() $\varphi ^M(p^*,\dot {c}^*)=(p^*\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }_{\beta (\nu ^*)}))$
.
$\varphi ^M(p^*,\dot {c}^*)=(p^*\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }_{\beta (\nu ^*)}))$
.
We claim that
![]() $p^*\Vdash \dot {\gamma }_{\beta (\nu ^*)}$
is a sup of
$p^*\Vdash \dot {\gamma }_{\beta (\nu ^*)}$
is a sup of
![]() $\langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
. Note that proving this claim suffices: indeed, then
$\langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
. Note that proving this claim suffices: indeed, then
![]() $p^*\upharpoonright \alpha $
forces that
$p^*\upharpoonright \alpha $
forces that
![]() $\dot {\gamma }_{\beta (\nu ^*)}$
is a sup of
$\dot {\gamma }_{\beta (\nu ^*)}$
is a sup of
![]() $\langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
, and as a result
$\langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
, and as a result
![]() $\varphi ^M(p^*,\dot {c}^*)=(p^*\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }_{\beta (\nu ^*)}))$
is a sup of
$\varphi ^M(p^*,\dot {c}^*)=(p^*\upharpoonright \alpha ,\pi _M^{-1}(\dot {\gamma }_{\beta (\nu ^*)}))$
is a sup of
![]() $\langle \varphi ^M(p_n,\dot {c}_n):n\in \omega \rangle $
.
$\langle \varphi ^M(p_n,\dot {c}_n):n\in \omega \rangle $
.
To prove the claim, we have two cases on
![]() $\nu ^*$
. Since
$\nu ^*$
. Since
![]() $\nu ^*=\sup _m\nu _m$
, either
$\nu ^*=\sup _m\nu _m$
, either
![]() $\nu ^*>\nu _m$
for all m, or
$\nu ^*>\nu _m$
for all m, or
![]() $\nu ^*=\nu _m$
for almost all m. In the first case,
$\nu ^*=\nu _m$
for almost all m. In the first case,
![]() $\nu ^*$
is a limit, and so
$\nu ^*$
is a limit, and so
![]() $\mathbb {P}$
forces that
$\mathbb {P}$
forces that
![]() $\dot {d}_{\nu ^*}$
is a sup of
$\dot {d}_{\nu ^*}$
is a sup of
![]() $\langle \dot {d}_\nu :\nu <\nu ^*\rangle $
. Since
$\langle \dot {d}_\nu :\nu <\nu ^*\rangle $
. Since
![]() $p_n\Vdash \dot {d}_{\nu _n}=^*\dot {\gamma }_{\beta (\nu _n)}$
for each n,
$p_n\Vdash \dot {d}_{\nu _n}=^*\dot {\gamma }_{\beta (\nu _n)}$
for each n,
![]() $p^*$
forces that
$p^*$
forces that
![]() $\langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
is cofinal in
$\langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
is cofinal in
![]() $\langle \dot {d}_\nu :\nu <\nu ^*\rangle $
. Therefore,
$\langle \dot {d}_\nu :\nu <\nu ^*\rangle $
. Therefore,
![]() $p^*$
forces that these two sequences have the same sups. Consequently,
$p^*$
forces that these two sequences have the same sups. Consequently,
![]() $p^*$
forces that
$p^*$
forces that
![]() $\dot {\gamma }_{\beta (\nu ^*)}=^*\dot {d}_{\nu ^*}$
is a sup of
$\dot {\gamma }_{\beta (\nu ^*)}=^*\dot {d}_{\nu ^*}$
is a sup of
![]() $\langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
. For the second case,
$\langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
. For the second case,
![]() $\nu ^*=\nu _m$
for all m above some k. Then
$\nu ^*=\nu _m$
for all m above some k. Then
![]() $\mathbb {P}$
forces that
$\mathbb {P}$
forces that
![]() $\langle \dot {d}_{\nu _n}:n\in \omega \rangle $
is eventually equal to
$\langle \dot {d}_{\nu _n}:n\in \omega \rangle $
is eventually equal to
![]() $\dot {d}_{\nu ^*}$
. Because
$\dot {d}_{\nu ^*}$
. Because
![]() $p_n\Vdash \dot {d}_{\nu _n}=^*\dot {\gamma }_{\beta (\nu _n)}$
for all n and
$p_n\Vdash \dot {d}_{\nu _n}=^*\dot {\gamma }_{\beta (\nu _n)}$
for all n and
![]() $p^*\geq p_n$
, we have that
$p^*\geq p_n$
, we have that
![]() $p^*\Vdash \langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
is eventually equal to
$p^*\Vdash \langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
is eventually equal to
![]() $\dot {d}_{\nu ^*}$
. Finally,
$\dot {d}_{\nu ^*}$
. Finally,
![]() $p^*\Vdash \dot {\gamma }_{\beta (\nu ^*)}=^*\dot {d}_{\nu ^*}$
, and therefore
$p^*\Vdash \dot {\gamma }_{\beta (\nu ^*)}=^*\dot {d}_{\nu ^*}$
, and therefore
![]() $p^*$
forces that
$p^*$
forces that
![]() $\langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
is eventually
$\langle \dot {\gamma }_{\beta (\nu _n)}:n\in \omega \rangle $
is eventually
![]() $=^*$
-equal to
$=^*$
-equal to
![]() $\dot {\gamma }_{\beta (\nu ^*)}$
, and therefore that
$\dot {\gamma }_{\beta (\nu ^*)}$
, and therefore that
![]() $\dot {\gamma }_{\beta (\nu ^*)}$
is a sup. This finishes the proof of the claim and thereby the proof that
$\dot {\gamma }_{\beta (\nu ^*)}$
is a sup. This finishes the proof of the claim and thereby the proof that
![]() $\varphi ^M$
is
$\varphi ^M$
is
![]() $\omega $
-continuous.▪
$\omega $
-continuous.▪
The final result in this subsection shows that we can create filters which are guided by the collapse at
![]() $\alpha $
by using the generic surjection from
$\alpha $
by using the generic surjection from
![]() $\omega _1$
onto
$\omega _1$
onto
![]() $\alpha $
to guide extensions in the second coordinate. This combines ideas of collapse absorption with, as previously mentioned, Abraham’s use of guiding reals.
$\alpha $
to guide extensions in the second coordinate. This combines ideas of collapse absorption with, as previously mentioned, Abraham’s use of guiding reals.
Lemma 5.5 Suppose that
![]() $\dot {\mathbb {Q}}$
is a
$\dot {\mathbb {Q}}$
is a
![]() $(\mathbb {P}\upharpoonright \alpha )$
-name for a poset of size
$(\mathbb {P}\upharpoonright \alpha )$
-name for a poset of size
![]() $\alpha $
, which is
$\alpha $
, which is
![]() $\omega _1$
-closed with sups, and let
$\omega _1$
-closed with sups, and let
![]() $\langle \dot {\gamma }_i:i<\alpha \rangle $
be forced to enumerate all conditions in
$\langle \dot {\gamma }_i:i<\alpha \rangle $
be forced to enumerate all conditions in
![]() $\dot {\mathbb {Q}}$
. Let
$\dot {\mathbb {Q}}$
. Let
![]() $\dot {f}_\alpha $
be the
$\dot {f}_\alpha $
be the
![]() $\mathbb {P}$
-name for the standard surjection added from
$\mathbb {P}$
-name for the standard surjection added from
![]() $\omega _1$
onto
$\omega _1$
onto
![]() $\alpha $
.
$\alpha $
.
Suppose that
![]() $\dot {s}=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
is a sequence of
$\dot {s}=\langle \dot {d}_\nu :\nu <\omega _1\rangle $
is a sequence of
![]() $\mathbb {P}$
-names for conditions in
$\mathbb {P}$
-names for conditions in
![]() $\dot {\mathbb {Q}}$
forced by
$\dot {\mathbb {Q}}$
forced by
![]() $\mathbb {P}$
to satisfy the following properties:
$\mathbb {P}$
to satisfy the following properties:
-
(1)
 $\dot {s}$
is
$\dot {s}$
is
 $\leq _{\dot {\mathbb {Q}}}$
-increasing,
$\leq _{\dot {\mathbb {Q}}}$
-increasing,
 $\dot {d}_0$
names the trivial condition, and if
$\dot {d}_0$
names the trivial condition, and if
 $\nu $
is a limit, then
$\nu $
is a limit, then
 $\dot {d}_\nu $
is a
$\dot {d}_\nu $
is a
 $\leq _{\dot {\mathbb {Q}}}$
-sup of
$\leq _{\dot {\mathbb {Q}}}$
-sup of
 $\langle \dot {d}_\mu :\mu <\nu \rangle $
;
$\langle \dot {d}_\mu :\mu <\nu \rangle $
; -
(2) if
 $\nu <\omega _1$
and
$\nu <\omega _1$
and
 $\dot {\gamma }_{\dot {f}_\alpha (\nu )}$
extends
$\dot {\gamma }_{\dot {f}_\alpha (\nu )}$
extends
 $\dot {d}_\nu $
in
$\dot {d}_\nu $
in
 $\dot {\mathbb {Q}}$
, then
$\dot {\mathbb {Q}}$
, then
 $\dot {d}_{\nu +1}$
extends
$\dot {d}_{\nu +1}$
extends
 $\dot {\gamma }_{\dot {f}_\alpha (\nu )}$
; and
$\dot {\gamma }_{\dot {f}_\alpha (\nu )}$
; and -
(3) for each
 $\nu <\omega _1$
, the sequence
$\nu <\omega _1$
, the sequence
 $\langle \dot {d}_\mu :\mu \leq \nu \rangle $
is definable in
$\langle \dot {d}_\mu :\mu \leq \nu \rangle $
is definable in
 $V[\dot {G}\upharpoonright \alpha ]$
from
$V[\dot {G}\upharpoonright \alpha ]$
from
 $\dot {f}_\alpha \upharpoonright \nu $
.
$\dot {f}_\alpha \upharpoonright \nu $
.
Then
![]() $\dot {s}$
is guided by the collapse at
$\dot {s}$
is guided by the collapse at
![]() $\alpha $
for
$\alpha $
for
![]() $\dot {\mathbb {Q}}$
.
$\dot {\mathbb {Q}}$
.
In particular, there exists a
![]() $\mathbb {P}$
-name for a sequence which is guided by the collapse at
$\mathbb {P}$
-name for a sequence which is guided by the collapse at
![]() $\alpha $
for
$\alpha $
for
![]() $\dot {\mathbb {Q}}$
.
$\dot {\mathbb {Q}}$
.
Proof We will verify that items (1)–(3) of Definition 5.1 hold. Item (1) of the definition is immediate from assumption (1) of the lemma.
For item (2) of Definition 5.1, suppose that
![]() $p\in \mathbb {P}$
is a condition where
$p\in \mathbb {P}$
is a condition where
![]() $\operatorname {dom}(p(\alpha ))$
is an ordinal
$\operatorname {dom}(p(\alpha ))$
is an ordinal
![]() $\nu <\omega _1$
. Let G be V-generic over
$\nu <\omega _1$
. Let G be V-generic over
![]() $\mathbb {P}$
containing p, and let
$\mathbb {P}$
containing p, and let
![]() $\bar {G}:=G\cap (\mathbb {P}\upharpoonright \alpha )$
. For each
$\bar {G}:=G\cap (\mathbb {P}\upharpoonright \alpha )$
. For each
![]() $\mu \leq \nu $
, let
$\mu \leq \nu $
, let
![]() $d_\mu :=\dot {d}_\mu [G]$
, and let
$d_\mu :=\dot {d}_\mu [G]$
, and let
![]() $\beta (\mu )$
be an ordinal
$\beta (\mu )$
be an ordinal
![]() $<\alpha $
so that
$<\alpha $
so that
![]() $d_\mu =\dot {\gamma }_{\beta (\mu )}[\bar {G}]$
. By assumption (3) of the lemma, the sequence
$d_\mu =\dot {\gamma }_{\beta (\mu )}[\bar {G}]$
. By assumption (3) of the lemma, the sequence
![]() $\langle d_\mu :\mu \leq \nu \rangle $
is definable in
$\langle d_\mu :\mu \leq \nu \rangle $
is definable in
![]() $V[\bar {G}]$
from
$V[\bar {G}]$
from
![]() $f_\alpha \upharpoonright \nu =p(\alpha )$
. Therefore, there exists a condition
$f_\alpha \upharpoonright \nu =p(\alpha )$
. Therefore, there exists a condition
![]() $\bar {p}\geq p\upharpoonright \alpha $
with
$\bar {p}\geq p\upharpoonright \alpha $
with
![]() $\bar {p}\in \bar {G}$
so that
$\bar {p}\in \bar {G}$
so that
![]() $\bar {p}$
forces that
$\bar {p}$
forces that
![]() $\langle \dot {\gamma }_{\beta (\mu )}:\mu \leq \nu \rangle $
satisfies the definition with respect to
$\langle \dot {\gamma }_{\beta (\mu )}:\mu \leq \nu \rangle $
satisfies the definition with respect to
![]() $p(\alpha )$
. Then
$p(\alpha )$
. Then
![]() $p':=p\cup \bar {p}$
witnesses item (2) of Definition 5.1, since
$p':=p\cup \bar {p}$
witnesses item (2) of Definition 5.1, since
![]() $p'$
forces that
$p'$
forces that
![]() $\langle \dot {\gamma }_{\beta (\mu )}:\mu \leq \nu \rangle $
and
$\langle \dot {\gamma }_{\beta (\mu )}:\mu \leq \nu \rangle $
and
![]() $\langle \dot {d}_\mu :\mu \leq \nu \rangle $
both satisfy the same definition in
$\langle \dot {d}_\mu :\mu \leq \nu \rangle $
both satisfy the same definition in
![]() $V[\dot {\bar {G}}]$
with the parameter
$V[\dot {\bar {G}}]$
with the parameter
![]() $\dot {f}_\alpha \upharpoonright \nu =p(\alpha )$
.
$\dot {f}_\alpha \upharpoonright \nu =p(\alpha )$
.
Turning to item (3) of Definition 5.1, let
![]() $p'$
be a condition as in the previous paragraph. Fix a
$p'$
be a condition as in the previous paragraph. Fix a
![]() $(\mathbb {P}\upharpoonright \alpha )$
-name
$(\mathbb {P}\upharpoonright \alpha )$
-name
![]() $\dot {\gamma }$
for a
$\dot {\gamma }$
for a
![]() $\dot {\mathbb {Q}}$
-extension of
$\dot {\mathbb {Q}}$
-extension of
![]() $\dot {\gamma }_{\beta (\nu )}$
, and let
$\dot {\gamma }_{\beta (\nu )}$
, and let
![]() $\delta <\alpha $
and
$\delta <\alpha $
and
![]() $\bar {p}^*\geq p'\upharpoonright \alpha $
so that
$\bar {p}^*\geq p'\upharpoonright \alpha $
so that
![]() $\bar {p}^*\Vdash _{\mathbb {P}\upharpoonright \alpha }\dot {\gamma }=\dot {\gamma }_\delta $
. Define
$\bar {p}^*\Vdash _{\mathbb {P}\upharpoonright \alpha }\dot {\gamma }=\dot {\gamma }_\delta $
. Define
![]() $p^*$
to be the minimal extension of
$p^*$
to be the minimal extension of
![]() $\bar {p}^*\cup p'\upharpoonright [\alpha ,\kappa )$
so that
$\bar {p}^*\cup p'\upharpoonright [\alpha ,\kappa )$
so that
![]() $p^*\Vdash \dot {f}_\alpha (\nu )=\delta $
. Then
$p^*\Vdash \dot {f}_\alpha (\nu )=\delta $
. Then
![]() $p^*\Vdash \dot {\gamma }_{\dot {f}_\alpha (\nu )}\geq \dot {\gamma }_{\beta (\nu )}=^*\dot {d}_\nu $
, so there exists an extension
$p^*\Vdash \dot {\gamma }_{\dot {f}_\alpha (\nu )}\geq \dot {\gamma }_{\beta (\nu )}=^*\dot {d}_\nu $
, so there exists an extension
![]() $p^{**}$
of
$p^{**}$
of
![]() $p^*$
so that
$p^*$
so that
![]() $p^{**}$
forces
$p^{**}$
forces
![]() $\dot {d}_{\nu +1}\geq \dot {\gamma }_{\dot {f}_\alpha (\mu )}=\dot {\gamma }$
.
$\dot {d}_{\nu +1}\geq \dot {\gamma }_{\dot {f}_\alpha (\mu )}=\dot {\gamma }$
.
For the “in particular” claim of the lemma, define a sequence
![]() $\dot {s}$
by recursion so that it satisfies (1) and so that if
$\dot {s}$
by recursion so that it satisfies (1) and so that if
![]() $\nu <\omega _1$
, then
$\nu <\omega _1$
, then
![]() $\dot {d}_{\nu +1}$
is forced to be equal to
$\dot {d}_{\nu +1}$
is forced to be equal to
![]() $\gamma _{\dot {f}_\alpha (\nu )}$
if this extends
$\gamma _{\dot {f}_\alpha (\nu )}$
if this extends
![]() $\dot {d}_\nu $
, and otherwise equals
$\dot {d}_\nu $
, and otherwise equals
![]() $\dot {d}_\nu $
. Then (2) and (3) are also satisfied, so
$\dot {d}_\nu $
. Then (2) and (3) are also satisfied, so
![]() $\dot {s}$
is guided by the collapse at
$\dot {s}$
is guided by the collapse at
![]() $\alpha $
for
$\alpha $
for
![]() $\dot {\mathbb {Q}}$
.▪
$\dot {\mathbb {Q}}$
.▪
5.2
 ${\mathcal {F}}$
-complete properness
${\mathcal {F}}$
-complete properness
We are now ready to isolate a sufficient condition on names
![]() $\dot {\mathbb {C}}$
so that
$\dot {\mathbb {C}}$
so that
![]() $\mathbb {P}\ast \dot {\mathbb {C}}$
is
$\mathbb {P}\ast \dot {\mathbb {C}}$
is
![]() ${\mathcal {F}}$
-strongly proper.
${\mathcal {F}}$
-strongly proper.
Definition 5.3 Let
![]() $\dot {\mathbb {C}}$
be a
$\dot {\mathbb {C}}$
be a
![]() $\mathbb {P}$
-name in
$\mathbb {P}$
-name in
![]() $H(\kappa ^+)$
for a poset forced to be
$H(\kappa ^+)$
for a poset forced to be
![]() $\omega _1$
-closed with sups. We say that
$\omega _1$
-closed with sups. We say that
![]() $\dot {\mathbb {C}}$
is
$\dot {\mathbb {C}}$
is
![]() ${\mathcal {F}}$
-Completely Proper if for any
${\mathcal {F}}$
-Completely Proper if for any
![]() $(\mathbb {P}\ast \dot {\mathbb {C}})$
-suitable sequence
$(\mathbb {P}\ast \dot {\mathbb {C}})$
-suitable sequence
![]() $\vec {M}$
, there is some
$\vec {M}$
, there is some
![]() $A\subseteq \operatorname {dom}(\vec {M})$
with
$A\subseteq \operatorname {dom}(\vec {M})$
with
![]() $A\in \mathcal {I}$
so that for each
$A\in \mathcal {I}$
so that for each
![]() $\alpha \in \operatorname {dom}(\vec {M})\backslash A$
and each
$\alpha \in \operatorname {dom}(\vec {M})\backslash A$
and each
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {H}$
for filter over
$\dot {H}$
for filter over
![]() $\pi _{M_\alpha }(\dot {\mathbb {C}})$
which is guided by the collapse at
$\pi _{M_\alpha }(\dot {\mathbb {C}})$
which is guided by the collapse at
![]() $\alpha $
, there exists a
$\alpha $
, there exists a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {c}_{\dot {H}}$
for a condition in
$\dot {c}_{\dot {H}}$
for a condition in
![]() $\dot {\mathbb {C}}$
which is forced to be a least upper bound for
$\dot {\mathbb {C}}$
which is forced to be a least upper bound for
![]() $\pi ^{-1}_{M_\alpha [\dot {G}_{\mathbb {P}}]}[\dot {H}]$
.
$\pi ^{-1}_{M_\alpha [\dot {G}_{\mathbb {P}}]}[\dot {H}]$
.
We recall that a poset
![]() $\mathbb {U}$
is
$\mathbb {U}$
is
![]() $\lambda $
-distributive if forcing with
$\lambda $
-distributive if forcing with
![]() $\mathbb {U}$
adds no sequences of ordinals of length less than
$\mathbb {U}$
adds no sequences of ordinals of length less than
![]() $\lambda $
. A sufficient condition to guarantee this is that the intersection of fewer than
$\lambda $
. A sufficient condition to guarantee this is that the intersection of fewer than
![]() $\lambda $
-many dense, open subsets of
$\lambda $
-many dense, open subsets of
![]() $\mathbb {U}$
is dense, open. They are equivalent if
$\mathbb {U}$
is dense, open. They are equivalent if
![]() $\mathbb {U}$
is separative.
$\mathbb {U}$
is separative.
Lemma 5.6 Suppose that
![]() $\dot {\mathbb {C}}$
is
$\dot {\mathbb {C}}$
is
![]() ${\mathcal {F}}$
-completely proper. Then
${\mathcal {F}}$
-completely proper. Then
![]() $\mathbb {P}$
forces that the intersection of fewer than
$\mathbb {P}$
forces that the intersection of fewer than
![]() $\kappa $
-many dense, open subsets of
$\kappa $
-many dense, open subsets of
![]() $\dot {\mathbb {C}}$
is dense, open. Hence,
$\dot {\mathbb {C}}$
is dense, open. Hence,
![]() $\dot {\mathbb {C}}$
is forced to be
$\dot {\mathbb {C}}$
is forced to be
![]() $\kappa $
-distributive.
$\kappa $
-distributive.
Proof Let
![]() $\vec {D}=\langle \dot {D}_i:i<\omega _1\rangle $
be a sequence of
$\vec {D}=\langle \dot {D}_i:i<\omega _1\rangle $
be a sequence of
![]() $\mathbb {P}$
-names for dense, open subsets of
$\mathbb {P}$
-names for dense, open subsets of
![]() $\dot {\mathbb {C}}$
. We show that the intersection is forced to be nonempty. Fix a sequence
$\dot {\mathbb {C}}$
. We show that the intersection is forced to be nonempty. Fix a sequence
![]() $\vec {M}$
which is suitable with respect to
$\vec {M}$
which is suitable with respect to
![]() $\mathbb {P}\ast \dot {\mathbb {C}}$
and
$\mathbb {P}\ast \dot {\mathbb {C}}$
and
![]() $\vec {D}$
so that
$\vec {D}$
so that
![]() $\operatorname {dom}(\vec {M})$
satisfies the conclusion of Definition 5.3. Let
$\operatorname {dom}(\vec {M})$
satisfies the conclusion of Definition 5.3. Let
![]() $\alpha \in \operatorname {dom}(\vec {M})$
. By Lemma 5.5, there exists a
$\alpha \in \operatorname {dom}(\vec {M})$
. By Lemma 5.5, there exists a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {H}$
for a filter which is guided by the collapse at
$\dot {H}$
for a filter which is guided by the collapse at
![]() $\alpha $
for
$\alpha $
for
![]() $\pi _{M_\alpha }(\dot {\mathbb {C}})$
. Since
$\pi _{M_\alpha }(\dot {\mathbb {C}})$
. Since
![]() $\operatorname {dom}(\vec {M})$
satisfies Definition 5.3, we may find a
$\operatorname {dom}(\vec {M})$
satisfies Definition 5.3, we may find a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {d}$
for a condition which is forced to be an upper bound in
$\dot {d}$
for a condition which is forced to be an upper bound in
![]() $\dot {\mathbb {C}}$
for
$\dot {\mathbb {C}}$
for
![]() $\pi ^{-1}_{M_\alpha [\dot {G}_{\mathbb {P}}]}[\dot {H}]$
. Then, by Lemma 5.2,
$\pi ^{-1}_{M_\alpha [\dot {G}_{\mathbb {P}}]}[\dot {H}]$
. Then, by Lemma 5.2,
![]() $\dot {d}$
is forced to be an
$\dot {d}$
is forced to be an
![]() $(M_\alpha [\dot {G}],\dot {\mathbb {C}})$
-completely generic condition. However,
$(M_\alpha [\dot {G}],\dot {\mathbb {C}})$
-completely generic condition. However,
![]() $\dot {D}_i\in M_\alpha $
for each
$\dot {D}_i\in M_\alpha $
for each
![]() $i<\omega _1$
and is dense, open. Therefore, it is forced that
$i<\omega _1$
and is dense, open. Therefore, it is forced that
![]() $\dot {d}\in \bigcap _{i\in \omega _1}\dot {D}_i$
.▪
$\dot {d}\in \bigcap _{i\in \omega _1}\dot {D}_i$
.▪
By combining Lemmas 2.12 and 5.5 and Proposition 5.4, we conclude with the following key result.
Proposition 5.7 Suppose that
![]() $\dot {\mathbb {C}}$
is
$\dot {\mathbb {C}}$
is
![]() ${\mathcal {F}}$
-completely proper. Then
${\mathcal {F}}$
-completely proper. Then
![]() $\mathbb {P}\ast \dot {\mathbb {C}}$
is
$\mathbb {P}\ast \dot {\mathbb {C}}$
is
![]() ${\mathcal {F}}$
-strongly proper.
${\mathcal {F}}$
-strongly proper.
6 Properties of the club-adding poset
In this section, we have two main tasks. In the first subsection, we will prove that our intended club-adding iteration, as well as useful variants thereof, are
![]() ${\mathcal {F}}$
-completely proper, and in the second subsection, we will prove that our intended club-adding iteration does not add branches through various Aronszajn trees. Each of these results will be used as part of a larger inductive argument in the final section in which we prove Theorem 1.1. Again, we comment that, in this case,
${\mathcal {F}}$
-completely proper, and in the second subsection, we will prove that our intended club-adding iteration does not add branches through various Aronszajn trees. Each of these results will be used as part of a larger inductive argument in the final section in which we prove Theorem 1.1. Again, we comment that, in this case,
![]() $\kappa $
is ineffable, but we are only using the ineffability of
$\kappa $
is ineffable, but we are only using the ineffability of
![]() $\kappa $
when we apply Proposition 4.4, since this requires Proposition 3.12.
$\kappa $
when we apply Proposition 4.4, since this requires Proposition 3.12.
6.1 Adding clubs is
 ${\mathcal {F}}$
-completely proper
${\mathcal {F}}$
-completely proper
In order to anticipate arguments in the next subsection, where we show that appropriate
![]() ${\mathcal {F}}$
-completely proper posets do not add branches through certain Aronszajn trees, we will need to not only show that our club-adding poset is
${\mathcal {F}}$
-completely proper posets do not add branches through certain Aronszajn trees, we will need to not only show that our club-adding poset is
![]() ${\mathcal {F}}$
-completely proper, but also show that variants of it have this property. These variants are created by iterating the process of taking an initial segment of the iteration followed by products of finitely many copies of the tail.
${\mathcal {F}}$
-completely proper, but also show that variants of it have this property. These variants are created by iterating the process of taking an initial segment of the iteration followed by products of finitely many copies of the tail.
The following iteration follows Magidor’s work [Reference Magidor31] on adding clubs through reflection points of stationary subsets of a weakly compact cardinal
![]() $\kappa $
, which has been collapsed to become
$\kappa $
, which has been collapsed to become
![]() $\omega _2$
.
$\omega _2$
.
Let
![]() $\rho <\kappa ^+$
, and suppose that we have defined a
$\rho <\kappa ^+$
, and suppose that we have defined a
![]() $\mathbb {P}$
-name for an iteration
$\mathbb {P}$
-name for an iteration
![]() $\langle \dot {\mathbb {C}}_\sigma ,\dot {\mathbb {C}}(\eta ):\sigma \leq \rho ,\eta <\rho \rangle $
and a
$\langle \dot {\mathbb {C}}_\sigma ,\dot {\mathbb {C}}(\eta ):\sigma \leq \rho ,\eta <\rho \rangle $
and a
![]() $(\mathbb {P}\ast \dot {\mathbb {C}}_\rho )$
-name
$(\mathbb {P}\ast \dot {\mathbb {C}}_\rho )$
-name
![]() $\langle \dot {\mathbb {S}}_\sigma ,\dot {\mathbb {S}}(\eta ):\sigma \leq \rho ,\eta <\rho \rangle $
for an iteration so that for all
$\langle \dot {\mathbb {S}}_\sigma ,\dot {\mathbb {S}}(\eta ):\sigma \leq \rho ,\eta <\rho \rangle $
for an iteration so that for all
![]() $\sigma <\rho $
the following assumptions are satisfied:
$\sigma <\rho $
the following assumptions are satisfied:
-
(1)
 $\mathbb {P}$
forces that the iteration
$\mathbb {P}$
forces that the iteration
 $\langle \dot {\mathbb {C}}_\sigma ,\dot {\mathbb {C}}(\eta ):\sigma \leq \rho ,\eta <\rho \rangle $
has
$\langle \dot {\mathbb {C}}_\sigma ,\dot {\mathbb {C}}(\eta ):\sigma \leq \rho ,\eta <\rho \rangle $
has
 $<\kappa $
-support, and
$<\kappa $
-support, and
 $\mathbb {P}\ast \dot {\mathbb {C}}_\rho $
forces that
$\mathbb {P}\ast \dot {\mathbb {C}}_\rho $
forces that
 $\langle \dot {\mathbb {S}}_\sigma ,\dot {\mathbb {S}}(\eta ):\sigma \leq \rho ,\eta <\rho \rangle $
has countable support. Furthermore,
$\langle \dot {\mathbb {S}}_\sigma ,\dot {\mathbb {S}}(\eta ):\sigma \leq \rho ,\eta <\rho \rangle $
has countable support. Furthermore,
 $\dot {\mathbb {S}}_\sigma $
is a
$\dot {\mathbb {S}}_\sigma $
is a
 $(\mathbb {P}\ast \dot {\mathbb {C}}_\sigma )$
-name
$(\mathbb {P}\ast \dot {\mathbb {C}}_\sigma )$
-name -
(2)
 $\dot {\mathbb {C}}(\sigma )$
is a
$\dot {\mathbb {C}}(\sigma )$
is a
 $(\mathbb {P}\ast \dot {\mathbb {C}}_\sigma )$
-name for
$(\mathbb {P}\ast \dot {\mathbb {C}}_\sigma )$
-name for
 $\mathsf {CU}(\dot {S}_\sigma ,\dot {\mathbb {S}}_\sigma )$
(see Definition 1.3), where
$\mathsf {CU}(\dot {S}_\sigma ,\dot {\mathbb {S}}_\sigma )$
(see Definition 1.3), where
 $\dot {S}_\sigma $
is a
$\dot {S}_\sigma $
is a
 $(\mathbb {P}\ast \dot {\mathbb {C}}_\sigma \ast \dot {\mathbb {S}}_\sigma )$
-name for a stationary subset of
$(\mathbb {P}\ast \dot {\mathbb {C}}_\sigma \ast \dot {\mathbb {S}}_\sigma )$
-name for a stationary subset of
 $\kappa \cap \operatorname {cof}(\omega )$
and
$\kappa \cap \operatorname {cof}(\omega )$
and
 $\dot {\mathbb {C}}_{\sigma +1}=\dot {\mathbb {C}}_\sigma \ast \dot {\mathbb {C}}(\sigma )$
.
$\dot {\mathbb {C}}_{\sigma +1}=\dot {\mathbb {C}}_\sigma \ast \dot {\mathbb {C}}(\sigma )$
. -
(3)
 $\dot {\mathbb {S}}(\sigma )$
is a
$\dot {\mathbb {S}}(\sigma )$
is a
 $(\mathbb {P}\ast \dot {\mathbb {C}}_{\sigma +1}\ast \dot {\mathbb {S}}_\sigma )$
-name for
$(\mathbb {P}\ast \dot {\mathbb {C}}_{\sigma +1}\ast \dot {\mathbb {S}}_\sigma )$
-name for
 $\mathbb {S}(\dot {T}_\sigma )$
(see Definition 1.4), where
$\mathbb {S}(\dot {T}_\sigma )$
(see Definition 1.4), where
 $\dot {T}_\sigma $
is a
$\dot {T}_\sigma $
is a
 $(\mathbb {P}\ast \dot {\mathbb {C}}_{\sigma +1}\ast \dot {\mathbb {S}}_\sigma )$
-name for an Aronszajn tree on
$(\mathbb {P}\ast \dot {\mathbb {C}}_{\sigma +1}\ast \dot {\mathbb {S}}_\sigma )$
-name for an Aronszajn tree on
 $\kappa $
.
$\kappa $
. -
(4)
 $\dot {\mathbb {C}}_\sigma $
is
$\dot {\mathbb {C}}_\sigma $
is
 ${\mathcal {F}}$
-completely proper (and hence
${\mathcal {F}}$
-completely proper (and hence
 $\mathbb {P}\ast \dot {\mathbb {C}}_\sigma $
is
$\mathbb {P}\ast \dot {\mathbb {C}}_\sigma $
is
 $\mathcal {F}$
-strongly proper, by Proposition 5.7), and
$\mathcal {F}$
-strongly proper, by Proposition 5.7), and
 $\mathbb {P}\ast \dot {\mathbb {C}}_\sigma $
forces that
$\mathbb {P}\ast \dot {\mathbb {C}}_\sigma $
forces that
 $\dot {\mathbb {S}}_\sigma $
is a countable support iteration specializing Aronszajn trees, as defined in Section 3.
$\dot {\mathbb {S}}_\sigma $
is a countable support iteration specializing Aronszajn trees, as defined in Section 3.
Working in an arbitrary generic extension by
![]() $\mathbb {P}$
, we now define the variations of
$\mathbb {P}$
, we now define the variations of
![]() $\dot {\mathbb {C}}_\rho $
mentioned above; we call these Doubling Tail Products. These will be the posets
$\dot {\mathbb {C}}_\rho $
mentioned above; we call these Doubling Tail Products. These will be the posets
![]() $\mathbb {C}_\rho (\vec {\delta })$
, where
$\mathbb {C}_\rho (\vec {\delta })$
, where
![]() $\vec {\delta } = \langle \delta _0,\delta _1,\dots ,\delta _{n-1}\rangle \in [\rho ]^n$
is a strictly decreasing sequence of ordinals. We use
$\vec {\delta } = \langle \delta _0,\delta _1,\dots ,\delta _{n-1}\rangle \in [\rho ]^n$
is a strictly decreasing sequence of ordinals. We use
![]() $[\rho ]^{<\omega }_{\text {dec}}$
to denote the set of all finite, strictly decreasing tuples from
$[\rho ]^{<\omega }_{\text {dec}}$
to denote the set of all finite, strictly decreasing tuples from
![]() $\rho $
;
$\rho $
;
![]() $[\rho ]^n_{\text {dec}}$
is defined similarly.
$[\rho ]^n_{\text {dec}}$
is defined similarly.
We first introduce an auxiliary name for a poset
![]() $\dot {\mathbb {C}}_{\delta ^*,\rho }(\vec {\delta })$
, where
$\dot {\mathbb {C}}_{\delta ^*,\rho }(\vec {\delta })$
, where
![]() $\vec {\delta }$
is as above and
$\vec {\delta }$
is as above and
![]() $\delta ^*\leq \delta _{n-1}$
is an additional ordinal. This is done by recursion on
$\delta ^*\leq \delta _{n-1}$
is an additional ordinal. This is done by recursion on
![]() $n = |\vec {\delta }|$
as follows:
$n = |\vec {\delta }|$
as follows:
-
• For
 $n = 0$
(i.e.,
$n = 0$
(i.e.,
 $\vec {\delta } = \emptyset $
), we define
$\vec {\delta } = \emptyset $
), we define
 $\dot {\mathbb {C}}_{\delta ^*,\rho }(\emptyset ) = \dot {\mathbb {C}}_{\delta ^*,\rho }$
to be the tail segment of the iteration
$\dot {\mathbb {C}}_{\delta ^*,\rho }(\emptyset ) = \dot {\mathbb {C}}_{\delta ^*,\rho }$
to be the tail segment of the iteration
 $\mathbb {C}_\rho $
, starting from stage
$\mathbb {C}_\rho $
, starting from stage
 $\delta ^*$
.
$\delta ^*$
. -
• For
 $n \geq 1$
,
$n \geq 1$
,
 $\vec {\delta } \in [\rho ]^n$
, and
$\vec {\delta } \in [\rho ]^n$
, and
 $\delta ^* \leq \delta _{n-1}$
, the poset
$\delta ^* \leq \delta _{n-1}$
, the poset
 $\mathbb {C}_{\delta ^*,\rho }(\vec {\delta })$
is given by where
$\mathbb {C}_{\delta ^*,\rho }(\vec {\delta })$
is given by where $$\begin{align*}\dot{\mathbb{C}}_{\delta^*,\rho}(\vec{\delta}) = \dot{\mathbb{C}}_{\delta^*,\delta_{n-1}} * (\dot{\mathbb{C}}_{\delta_{n-1},\rho}(\vec{\delta}\upharpoonright n-1))^2,\end{align*}$$
$$\begin{align*}\dot{\mathbb{C}}_{\delta^*,\rho}(\vec{\delta}) = \dot{\mathbb{C}}_{\delta^*,\delta_{n-1}} * (\dot{\mathbb{C}}_{\delta_{n-1},\rho}(\vec{\delta}\upharpoonright n-1))^2,\end{align*}$$
 $\dot {\mathbb {C}}_{\delta ^*,\delta _{n-1}}$
is the segment of the iteration
$\dot {\mathbb {C}}_{\delta ^*,\delta _{n-1}}$
is the segment of the iteration
 $\mathbb {C}_\rho $
starting from (and including) stage
$\mathbb {C}_\rho $
starting from (and including) stage
 $\delta ^*$
to stage
$\delta ^*$
to stage
 $\delta _{n-1}$
, and
$\delta _{n-1}$
, and
 $\vec {\delta }\upharpoonright (n-1) = \langle \delta _0,\dots ,\delta _{n-2} \rangle $
.
$\vec {\delta }\upharpoonright (n-1) = \langle \delta _0,\dots ,\delta _{n-2} \rangle $
.
We can now define
![]() $\mathbb {C}_{\rho }(\vec {\delta })$
.
$\mathbb {C}_{\rho }(\vec {\delta })$
.
Definition 6.1 For
![]() $\vec {\delta } \in [\rho ]^{<\omega }_{\text {dec}}$
, define
$\vec {\delta } \in [\rho ]^{<\omega }_{\text {dec}}$
, define
![]() $\mathbb {C}_\rho (\vec {\delta }) = \mathbb {C}_{0,\rho }(\vec {\delta })$
(i.e., as
$\mathbb {C}_\rho (\vec {\delta }) = \mathbb {C}_{0,\rho }(\vec {\delta })$
(i.e., as
![]() $\mathbb {C}_{\delta ^*,\rho }(\vec {\delta })$
with
$\mathbb {C}_{\delta ^*,\rho }(\vec {\delta })$
with
![]() $\delta ^* =0$
).
$\delta ^* =0$
).
For example, if
![]() $\vec {\delta } = \langle \delta _0\rangle $
is a singleton, then
$\vec {\delta } = \langle \delta _0\rangle $
is a singleton, then
![]() $\mathbb {C}_{\rho }(\langle \delta _0 \rangle ) = \mathbb {C}_{\delta _0}* \dot {\mathbb {C}}_{\delta _0,\rho }^2$
. Similarly, if
$\mathbb {C}_{\rho }(\langle \delta _0 \rangle ) = \mathbb {C}_{\delta _0}* \dot {\mathbb {C}}_{\delta _0,\rho }^2$
. Similarly, if
![]() $\vec {\delta } = \langle \delta _0,\delta _1\rangle $
has two elements
$\vec {\delta } = \langle \delta _0,\delta _1\rangle $
has two elements
![]() $\delta _0> \delta _1$
, then
$\delta _0> \delta _1$
, then
We refer to posets
![]() $\mathbb {C}_\rho (\vec {\delta })$
as the doubling tail products of
$\mathbb {C}_\rho (\vec {\delta })$
as the doubling tail products of
![]() $\mathbb {C}_\rho $
. We now return to working in V, in particular with the statement of the next item.
$\mathbb {C}_\rho $
. We now return to working in V, in particular with the statement of the next item.
Proposition 6.1 (Given assumptions (1)–(4) stated at the beginning of the subsection) For each
![]() $\rho < \kappa ^+$
and
$\rho < \kappa ^+$
and
![]() $\vec {\delta } = \langle \delta _{0},\dots ,\delta _{n-1}\rangle \in [\rho ]^{<\omega }_{\text {dec}}$
, the doubling tail product
$\vec {\delta } = \langle \delta _{0},\dots ,\delta _{n-1}\rangle \in [\rho ]^{<\omega }_{\text {dec}}$
, the doubling tail product
![]() $\dot {\mathbb {C}}_\rho (\vec {\delta })$
is
$\dot {\mathbb {C}}_\rho (\vec {\delta })$
is
![]() ${\mathcal {F}}$
-completely proper. In particular,
${\mathcal {F}}$
-completely proper. In particular,
![]() $\dot {\mathbb {C}}_\rho $
is
$\dot {\mathbb {C}}_\rho $
is
![]() ${\mathcal {F}}$
-completely proper.
${\mathcal {F}}$
-completely proper.
We will explain the necessity of proving Proposition 6.1 for the doubling tail products of
![]() $\dot {\mathbb {C}}_\rho $
in the final section of the paper.
$\dot {\mathbb {C}}_\rho $
in the final section of the paper.
Proof We will first work with
![]() $\dot {\mathbb {C}}_\rho $
, rather than with the doubling tail products, in order to establish that a certain statement
$\dot {\mathbb {C}}_\rho $
, rather than with the doubling tail products, in order to establish that a certain statement
![]() $(*)$
(see below) holds. We will then show that this statement
$(*)$
(see below) holds. We will then show that this statement
![]() $(*)$
can be used to prove the desired result for the doubling tail products. We use
$(*)$
can be used to prove the desired result for the doubling tail products. We use
![]() $\mathbb {R}_\sigma $
, for
$\mathbb {R}_\sigma $
, for
![]() $\sigma \leq \rho $
, to denote
$\sigma \leq \rho $
, to denote
![]() $\mathbb {P}\ast \dot {\mathbb {C}}_\sigma *\dot {\mathbb {S}}_\sigma $
.
$\mathbb {P}\ast \dot {\mathbb {C}}_\sigma *\dot {\mathbb {S}}_\sigma $
.
To begin, we fix an
![]() $\mathbb {R}_\rho $
-suitable sequence
$\mathbb {R}_\rho $
-suitable sequence
![]() $\vec {M}$
; by removing a set in
$\vec {M}$
; by removing a set in
![]() $\mathcal {I}$
, we may assume that
$\mathcal {I}$
, we may assume that
![]() $\vec {M}$
is in pre-splitting configuration up to
$\vec {M}$
is in pre-splitting configuration up to
![]() $\rho $
. By removing a further
$\rho $
. By removing a further
![]() $\mathcal {I}$
-null set, we may assume that
$\mathcal {I}$
-null set, we may assume that
![]() $\vec {M}$
satisfies the conclusion of Proposition 4.4.
$\vec {M}$
satisfies the conclusion of Proposition 4.4.
Let M be a
![]() $\kappa $
-model so that M contains the relevant parameters, including
$\kappa $
-model so that M contains the relevant parameters, including
![]() $\vec {M}$
. Since
$\vec {M}$
. Since
![]() $\operatorname {dom}(\vec {M})$
is in
$\operatorname {dom}(\vec {M})$
is in
![]() $\mathcal {F}^+$
, we may apply Proposition 1.4 to find an M-normal ultrafilter U so that, letting
$\mathcal {F}^+$
, we may apply Proposition 1.4 to find an M-normal ultrafilter U so that, letting
![]() $j:M\longrightarrow N$
be the corresponding ultrapower map,
$j:M\longrightarrow N$
be the corresponding ultrapower map,
![]() $\kappa \in j(\operatorname {dom}(\vec {M}))$
. Let
$\kappa \in j(\operatorname {dom}(\vec {M}))$
. Let
![]() $M_\kappa $
be the
$M_\kappa $
be the
![]() $\kappa $
th model on the sequence
$\kappa $
th model on the sequence
![]() $j(\vec {M})$
.
$j(\vec {M})$
.
Fix a V-generic filter
![]() $G^*$
over
$G^*$
over
![]() $j(\mathbb {P})$
, and let
$j(\mathbb {P})$
, and let
![]() $G:=G^*\cap \mathbb {P}$
. For notational simplicity, we continue using j to denote the lifted map
$G:=G^*\cap \mathbb {P}$
. For notational simplicity, we continue using j to denote the lifted map
![]() $j:M[G]\longrightarrow N[G^*]$
. Recall by Lemma 2.11 that
$j:M[G]\longrightarrow N[G^*]$
. Recall by Lemma 2.11 that
![]() $j^{-1}\upharpoonright M_\kappa $
is the transitive collapse map of
$j^{-1}\upharpoonright M_\kappa $
is the transitive collapse map of
![]() $M_\kappa $
and that
$M_\kappa $
and that
![]() $j^{-1}$
lifts in the standard way to
$j^{-1}$
lifts in the standard way to
![]() $M_\kappa [G^*]$
.
$M_\kappa [G^*]$
.
Suppose that
![]() $\sigma \leq \rho $
and that
$\sigma \leq \rho $
and that
![]() $\dot {H}$
is a
$\dot {H}$
is a
![]() $j(\mathbb {P})$
-name in N for a generic filter over
$j(\mathbb {P})$
-name in N for a generic filter over
![]() $\pi _{M_\kappa [\dot {G}^*]}(j(\dot {\mathbb {C}}_\sigma ))=\dot {\mathbb {C}}_\sigma $
. We define the
$\pi _{M_\kappa [\dot {G}^*]}(j(\dot {\mathbb {C}}_\sigma ))=\dot {\mathbb {C}}_\sigma $
. We define the
![]() $\kappa $
-flat function for (the pullback of)
$\kappa $
-flat function for (the pullback of)
![]() $\dot {H}$
to be the
$\dot {H}$
to be the
![]() $j(\mathbb {P})$
-name for the function with domain
$j(\mathbb {P})$
-name for the function with domain
![]() $j[\sigma ]$
,Footnote
6
so that for each
$j[\sigma ]$
,Footnote
6
so that for each
![]() $\eta <\sigma $
,
$\eta <\sigma $
,
![]() $\dot {r}(j(\eta ))$
is forced to be equal to
$\dot {r}(j(\eta ))$
is forced to be equal to
![]() $\left (\bigcup \dot {H}(\eta )\right )\cup \left \{\kappa \right \}$
.
$\left (\bigcup \dot {H}(\eta )\right )\cup \left \{\kappa \right \}$
.
We will prove the following proposition
![]() $(*)$
by induction:
$(*)$
by induction:
-
(*) for any
 $\sigma \leq \rho $
, if
$\sigma \leq \rho $
, if
 $\dot {H}$
is a
$\dot {H}$
is a
 $j(\mathbb {P})$
-name in N for a generic filter over
$j(\mathbb {P})$
-name in N for a generic filter over
 $\dot {\mathbb {C}}_\sigma =\pi _{M_\kappa [G^*]}(j(\dot {\mathbb {C}}_\sigma ))$
which is guided by the collapse at
$\dot {\mathbb {C}}_\sigma =\pi _{M_\kappa [G^*]}(j(\dot {\mathbb {C}}_\sigma ))$
which is guided by the collapse at
 $\kappa $
(see Definition 5.2), then it is forced by
$\kappa $
(see Definition 5.2), then it is forced by
 $j(\mathbb {P})$
that the
$j(\mathbb {P})$
that the
 $\kappa $
-flat function for
$\kappa $
-flat function for
 $\dot {H}$
is a condition in
$\dot {H}$
is a condition in
 $j(\dot {\mathbb {C}}_\sigma )$
.
$j(\dot {\mathbb {C}}_\sigma )$
.
We first consider the case that
![]() $\sigma \leq \rho $
is limit. Suppose that we know the result for all
$\sigma \leq \rho $
is limit. Suppose that we know the result for all
![]() $\eta <\sigma $
. We use throughout the fact that
$\eta <\sigma $
. We use throughout the fact that
![]() $j^{-1}$
equals the transitive collapse map of
$j^{-1}$
equals the transitive collapse map of
![]() $M_\kappa [G^*]$
.
$M_\kappa [G^*]$
.
Let
![]() $H\in N[G^*]$
be a filter over
$H\in N[G^*]$
be a filter over
![]() $\mathbb {C}_\sigma $
which is guided by the collapse at
$\mathbb {C}_\sigma $
which is guided by the collapse at
![]() $\kappa $
, and let r be the
$\kappa $
, and let r be the
![]() $\kappa $
-flat function for H. Since
$\kappa $
-flat function for H. Since
![]() $|\operatorname {dom}(r)|^N<j(\kappa )$
and
$|\operatorname {dom}(r)|^N<j(\kappa )$
and
![]() $j(\mathbb {C}_\sigma )$
is taken with
$j(\mathbb {C}_\sigma )$
is taken with
![]() $<j(\kappa )$
-supports, in order to see that
$<j(\kappa )$
-supports, in order to see that
![]() $r\in j(\mathbb {C}_\sigma )$
, it suffices to show that for all
$r\in j(\mathbb {C}_\sigma )$
, it suffices to show that for all
![]() $\eta <\sigma $
,
$\eta <\sigma $
,
![]() $r\upharpoonright j(\eta )\in j(\mathbb {C}_\eta ).$
So let
$r\upharpoonright j(\eta )\in j(\mathbb {C}_\eta ).$
So let
![]() $\eta <\sigma $
be fixed. Since
$\eta <\sigma $
be fixed. Since
![]() $\mathbb {C}_\sigma \cong \mathbb {C}_\eta \ast \dot {\mathbb {C}}_{{\eta },\sigma }$
and since H is guided by the collapse at
$\mathbb {C}_\sigma \cong \mathbb {C}_\eta \ast \dot {\mathbb {C}}_{{\eta },\sigma }$
and since H is guided by the collapse at
![]() $\kappa $
over
$\kappa $
over
![]() $\mathbb {C}_\sigma $
, we have by Lemma 5.3 that
$\mathbb {C}_\sigma $
, we have by Lemma 5.3 that
![]() $H\upharpoonright \mathbb {C}_\eta $
is also guided by the collapse at
$H\upharpoonright \mathbb {C}_\eta $
is also guided by the collapse at
![]() $\kappa $
over
$\kappa $
over
![]() $\mathbb {C}_\eta $
. By induction, this implies that the
$\mathbb {C}_\eta $
. By induction, this implies that the
![]() $\kappa $
-flat function for
$\kappa $
-flat function for
![]() $H\upharpoonright \mathbb {C}_\eta $
, namely
$H\upharpoonright \mathbb {C}_\eta $
, namely
![]() $r\upharpoonright j(\eta )$
, is a condition in
$r\upharpoonright j(\eta )$
, is a condition in
![]() $j(\mathbb {C}_\eta )$
. This completes the proof of
$j(\mathbb {C}_\eta )$
. This completes the proof of
![]() $(*)$
in the limit case.
$(*)$
in the limit case.
Now, suppose that
![]() $\sigma +1\leq \rho $
and that we know that
$\sigma +1\leq \rho $
and that we know that
![]() $(*)$
holds at
$(*)$
holds at
![]() $\sigma $
. Let
$\sigma $
. Let
![]() $H\in N[G^*]$
be a filter over
$H\in N[G^*]$
be a filter over
![]() $\mathbb {C}_{\sigma +1}$
which is guided by the collapse at
$\mathbb {C}_{\sigma +1}$
which is guided by the collapse at
![]() $\kappa $
, and let
$\kappa $
, and let
![]() $H_\sigma $
denote the restriction of H to
$H_\sigma $
denote the restriction of H to
![]() $\mathbb {C}_\sigma $
. Again, appealing to Lemma 5.3, we know that
$\mathbb {C}_\sigma $
. Again, appealing to Lemma 5.3, we know that
![]() $H_\sigma $
is guided by the collapse at
$H_\sigma $
is guided by the collapse at
![]() $\kappa $
.
$\kappa $
.
Let r be the
![]() $\kappa $
-flat function for H, and let
$\kappa $
-flat function for H, and let
![]() $\bar {r}$
denote
$\bar {r}$
denote
![]() $r\upharpoonright j(\sigma )$
, the
$r\upharpoonright j(\sigma )$
, the
![]() $\kappa $
-flat function for
$\kappa $
-flat function for
![]() $H_\sigma $
. Since
$H_\sigma $
. Since
![]() $H_\sigma $
is guided by the collapse at
$H_\sigma $
is guided by the collapse at
![]() $\kappa $
, we may apply the induction hypothesis to conclude that
$\kappa $
, we may apply the induction hypothesis to conclude that
![]() $\bar {r}$
is a condition in
$\bar {r}$
is a condition in
![]() $j(\mathbb {C}_\sigma )$
. By Proposition 5.4, since
$j(\mathbb {C}_\sigma )$
. By Proposition 5.4, since
![]() $H_\sigma $
is guided by the collapse at
$H_\sigma $
is guided by the collapse at
![]() $\kappa $
, we know that in N we may find a residue pair
$\kappa $
, we know that in N we may find a residue pair
![]() $\langle (0_{j(\mathbb {P})},\dot {\bar {r}}),\varphi ^{M_\kappa }\rangle $
for the pair
$\langle (0_{j(\mathbb {P})},\dot {\bar {r}}),\varphi ^{M_\kappa }\rangle $
for the pair
![]() $(M_\kappa ,j(\mathbb {P}^*))$
, where
$(M_\kappa ,j(\mathbb {P}^*))$
, where
![]() $\dot {\bar {r}}$
is a
$\dot {\bar {r}}$
is a
![]() $j(\mathbb {P})$
-name in N for
$j(\mathbb {P})$
-name in N for
![]() $\bar {r}$
. We use
$\bar {r}$
. We use
![]() $p^*(M_\kappa )$
to denote
$p^*(M_\kappa )$
to denote
![]() $(0_{j(\mathbb {P})},\dot {\bar {r}})$
.
$(0_{j(\mathbb {P})},\dot {\bar {r}})$
.
Since
![]() $\bar {r}$
is an upper bound for
$\bar {r}$
is an upper bound for
![]() $ \pi _{M_\kappa [G^*]}^{-1}[H_\sigma ]=j[H_\sigma ]$
, we conclude that
$ \pi _{M_\kappa [G^*]}^{-1}[H_\sigma ]=j[H_\sigma ]$
, we conclude that
![]() $\bar {r}$
forces in
$\bar {r}$
forces in
![]() $j(\mathbb {C}_\sigma )$
over
$j(\mathbb {C}_\sigma )$
over
![]() $N[G^*]$
that
$N[G^*]$
that
![]() $\bigcup j[H(\sigma )]{=\bigcup H(\sigma )}$
is club in
$\bigcup j[H(\sigma )]{=\bigcup H(\sigma )}$
is club in
![]() $\kappa $
(equality follows since j is the identity on bounded subsets of
$\kappa $
(equality follows since j is the identity on bounded subsets of
![]() $\kappa $
). Therefore, to see that
$\kappa $
). Therefore, to see that
![]() $r\in j(\mathbb {C}_{\sigma +1})$
(which finishes the proof of
$r\in j(\mathbb {C}_{\sigma +1})$
(which finishes the proof of
![]() $(*)$
in the successor case), it suffices to show that
$(*)$
in the successor case), it suffices to show that
Since
![]() $j(\dot {\mathbb {C}}(\sigma ))$
is a
$j(\dot {\mathbb {C}}(\sigma ))$
is a
![]() $j(\mathbb {P}\ast \dot {\mathbb {C}}_\sigma )$
-name for
$j(\mathbb {P}\ast \dot {\mathbb {C}}_\sigma )$
-name for
![]() $\mathsf {CU}(j(\dot {S}_\sigma ),j(\dot {\mathbb {S}}_\sigma ))$
, the above holds if and only if
$\mathsf {CU}(j(\dot {S}_\sigma ),j(\dot {\mathbb {S}}_\sigma ))$
, the above holds if and only if
By the elementarity of j and since
![]() $\bar {r}$
is an upper bound for
$\bar {r}$
is an upper bound for
![]() $j[H_\sigma ]$
, we see that
$j[H_\sigma ]$
, we see that
Since
![]() $\kappa $
has cofinality
$\kappa $
has cofinality
![]() $\omega _1$
after forcing with
$\omega _1$
after forcing with
![]() $j(\mathbb {C}_\sigma \ast \dot {\mathbb {S}}_\sigma )$
, it therefore suffices to show that
$j(\mathbb {C}_\sigma \ast \dot {\mathbb {S}}_\sigma )$
, it therefore suffices to show that
Before continuing, we recall that
![]() $\mathbb {R}_\sigma $
denotes
$\mathbb {R}_\sigma $
denotes
![]() $\mathbb {P}\ast \dot {\mathbb {C}}_\sigma \ast \dot {\mathbb {S}}_\sigma $
. By Proposition 3.2, we know that
$\mathbb {P}\ast \dot {\mathbb {C}}_\sigma \ast \dot {\mathbb {S}}_\sigma $
. By Proposition 3.2, we know that
However,
![]() $j(\mathbb {R}_\sigma )\cap M_\kappa =j[\mathbb {R}_\sigma ]$
is isomorphic to
$j(\mathbb {R}_\sigma )\cap M_\kappa =j[\mathbb {R}_\sigma ]$
is isomorphic to
![]() $\mathbb {R}_\sigma $
, and
$\mathbb {R}_\sigma $
, and
![]() $j(\dot {S}_\sigma )\cap M_\kappa =j[\dot {S}_\sigma ]$
. Since
$j(\dot {S}_\sigma )\cap M_\kappa =j[\dot {S}_\sigma ]$
. Since
![]() $\dot {S}_\sigma $
is a nice
$\dot {S}_\sigma $
is a nice
![]() $\mathbb {R}_\sigma $
-name for a stationary subset of
$\mathbb {R}_\sigma $
-name for a stationary subset of
![]() $\kappa \cap \operatorname {cof}(\omega )$
,
$\kappa \cap \operatorname {cof}(\omega )$
,
![]() $j[\dot {S}_\sigma ]$
is therefore a
$j[\dot {S}_\sigma ]$
is therefore a
![]() $j(\mathbb {R}_\sigma )\cap M_\kappa $
-name for a stationary subset of
$j(\mathbb {R}_\sigma )\cap M_\kappa $
-name for a stationary subset of
![]() $\kappa \cap \operatorname {cof}(\omega )$
.
$\kappa \cap \operatorname {cof}(\omega )$
.
We now apply Proposition 4.4 in N, recalling that
![]() $\vec {M}$
satisfies the conclusion of that proposition and that
$\vec {M}$
satisfies the conclusion of that proposition and that
![]() $\kappa \in j(\operatorname {dom}(\vec {M}))$
. Thus, applying the observations in the previous paragraph, we conclude that
$\kappa \in j(\operatorname {dom}(\vec {M}))$
. Thus, applying the observations in the previous paragraph, we conclude that
![]() $(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\sigma )})$
forces over N that
$(p^*(M_\kappa ),0_{j(\dot {\mathbb {S}}_\sigma )})$
forces over N that
![]() $j[\dot {S}_\sigma ]$
is stationary in
$j[\dot {S}_\sigma ]$
is stationary in
![]() $\kappa $
. Recalling that
$\kappa $
. Recalling that
![]() $p^*(M_\kappa )=(0_{j(\mathbb {P})},\dot {\bar {r}})$
, we now conclude that
$p^*(M_\kappa )=(0_{j(\mathbb {P})},\dot {\bar {r}})$
, we now conclude that
This completes the proof that r, the
![]() $\kappa $
-flat function for H, is a condition in
$\kappa $
-flat function for H, is a condition in
![]() $j(\mathbb {C}_\sigma )$
and also finishes the proof that
$j(\mathbb {C}_\sigma )$
and also finishes the proof that
![]() $(*)$
holds.
$(*)$
holds.
To finish the proof of Proposition 6.1, we prove by induction on
![]() $k<\omega $
that for any
$k<\omega $
that for any
![]() $\vec {\delta } = \langle \delta _0,\dots ,\delta _{k-1}\rangle \in [\rho ]^k_{\text {dec}}$
, the poset
$\vec {\delta } = \langle \delta _0,\dots ,\delta _{k-1}\rangle \in [\rho ]^k_{\text {dec}}$
, the poset
![]() $\mathbb {C}_\rho (\vec {\delta })$
is
$\mathbb {C}_\rho (\vec {\delta })$
is
![]() $\mathcal {F}$
-completely proper. Working by contradiction, let
$\mathcal {F}$
-completely proper. Working by contradiction, let
![]() $k\in \omega $
be the least so that for some (empty in case
$k\in \omega $
be the least so that for some (empty in case
![]() $k=0$
)
$k=0$
)
![]() $\vec {\delta }\in [\rho ]^k_{\text {dec}}$
, the proposition fails for
$\vec {\delta }\in [\rho ]^k_{\text {dec}}$
, the proposition fails for
![]() $\mathbb {C}_\rho (\vec {\delta })$
. Let
$\mathbb {C}_\rho (\vec {\delta })$
. Let
![]() $\vec {M}$
be a
$\vec {M}$
be a
![]() $\vec {\delta }$
-suitable sequence which witnesses that
$\vec {\delta }$
-suitable sequence which witnesses that
![]() $\mathbb {C}_\rho (\vec {\delta })$
is not
$\mathbb {C}_\rho (\vec {\delta })$
is not
![]() $\mathcal {F}$
-suitable. Since
$\mathcal {F}$
-suitable. Since
![]() $\vec {M}$
is
$\vec {M}$
is
![]() $\vec {\delta }$
-suitable it is also
$\vec {\delta }$
-suitable it is also
![]() $\mathbb {P}\ast \dot {\mathbb {C}}_\rho (\vec {\delta })$
-suitable. By removing an
$\mathbb {P}\ast \dot {\mathbb {C}}_\rho (\vec {\delta })$
-suitable. By removing an
![]() $\mathcal {I}$
-null set, we may assume that
$\mathcal {I}$
-null set, we may assume that
![]() $\vec {M}$
satisfies the conclusion of Proposition 4.4.
$\vec {M}$
satisfies the conclusion of Proposition 4.4.
Let M be a
![]() $\kappa $
-model containing the relevant parameters, including
$\kappa $
-model containing the relevant parameters, including
![]() $\vec {M}$
. Since
$\vec {M}$
. Since
![]() $\operatorname {dom}(\vec {M})\in {\mathcal {F}^+}$
, we may find some M-normal ultrafilter U so that, letting
$\operatorname {dom}(\vec {M})\in {\mathcal {F}^+}$
, we may find some M-normal ultrafilter U so that, letting
![]() $j:M\longrightarrow N$
be the ultrapower embedding,
$j:M\longrightarrow N$
be the ultrapower embedding,
![]() $\kappa \in j(\operatorname {dom}(\vec {M}))$
.
$\kappa \in j(\operatorname {dom}(\vec {M}))$
.
First, we deal with the case
![]() $k=0$
. Since
$k=0$
. Since
![]() $\vec {M}$
witnesses that
$\vec {M}$
witnesses that
![]() $\dot {\mathbb {C}}_\rho $
is not
$\dot {\mathbb {C}}_\rho $
is not
![]() $\mathcal {F}$
-completely proper, N satisfies that the conclusion of Definition 5.3 fails at
$\mathcal {F}$
-completely proper, N satisfies that the conclusion of Definition 5.3 fails at
![]() $\kappa $
with respect to
$\kappa $
with respect to
![]() $j(\mathbb {P})$
and
$j(\mathbb {P})$
and
![]() $j(\dot {\mathbb {C}}_\rho )$
. However, this directly contradicts
$j(\dot {\mathbb {C}}_\rho )$
. However, this directly contradicts
![]() $(*)$
, which we showed holds in this setup.
$(*)$
, which we showed holds in this setup.
Now, we assume that
![]() $k=l+1$
is a successor. Then we may find an N-generic filter
$k=l+1$
is a successor. Then we may find an N-generic filter
![]() $G^*$
over
$G^*$
over
![]() $j(\mathbb {P})$
so that in
$j(\mathbb {P})$
so that in
![]() $N[G^*]$
there is a filter
$N[G^*]$
there is a filter
![]() $H^*$
over
$H^*$
over
![]() $\pi _{{M_\kappa }[G^*]}(j(\mathbb {C}_\rho (\vec {\delta })))=\mathbb {C}_\rho (\vec {\delta })$
so that no condition in
$\pi _{{M_\kappa }[G^*]}(j(\mathbb {C}_\rho (\vec {\delta })))=\mathbb {C}_\rho (\vec {\delta })$
so that no condition in
![]() $j(\mathbb {C}_\rho (\vec {\delta }))$
is a least upper bound for
$j(\mathbb {C}_\rho (\vec {\delta }))$
is a least upper bound for
![]() $\pi ^{-1}_{M_\kappa [G^*]}[H^*]$
. We will show, on the contrary, that there is such a least upper bound for the pullback of
$\pi ^{-1}_{M_\kappa [G^*]}[H^*]$
. We will show, on the contrary, that there is such a least upper bound for the pullback of
![]() $H^*$
.
$H^*$
.
Write
![]() $\vec {\delta }=\langle \delta _0,\dots ,\delta _{k-1}\rangle $
. For simplicity of notation, we also write
$\vec {\delta }=\langle \delta _0,\dots ,\delta _{k-1}\rangle $
. For simplicity of notation, we also write
![]() $\mathbb {C}_\rho (\vec {\delta }\upharpoonright k-1)=\mathbb {C}_{\delta _{k-2}}\ast \dot {\mathbb {D}}$
so that
$\mathbb {C}_\rho (\vec {\delta }\upharpoonright k-1)=\mathbb {C}_{\delta _{k-2}}\ast \dot {\mathbb {D}}$
so that
![]() $\mathbb {C}_\rho (\vec {\delta })=\mathbb {C}_{\delta _{k-1}}\ast \left (\dot {\mathbb {C}}_{[\delta _{k-1},\delta _{k-2})}\ast \dot {\mathbb {D}}\right )^{2}$
. Note in the case
$\mathbb {C}_\rho (\vec {\delta })=\mathbb {C}_{\delta _{k-1}}\ast \left (\dot {\mathbb {C}}_{[\delta _{k-1},\delta _{k-2})}\ast \dot {\mathbb {D}}\right )^{2}$
. Note in the case
![]() $k=1$
, we just have
$k=1$
, we just have
![]() $\mathbb {C}_\rho (\vec {\delta })=\mathbb {C}_{\delta _0}\ast (\dot {\mathbb {C}}_{[\delta _0,\rho )})^2$
. The filter
$\mathbb {C}_\rho (\vec {\delta })=\mathbb {C}_{\delta _0}\ast (\dot {\mathbb {C}}_{[\delta _0,\rho )})^2$
. The filter
![]() $H^*$
adds generics
$H^*$
adds generics
![]() $J_0,J_1$
over
$J_0,J_1$
over
![]() $\mathbb {C}_{\rho }(\vec {\delta }\upharpoonright k-1)$
so that
$\mathbb {C}_{\rho }(\vec {\delta }\upharpoonright k-1)$
so that
![]() $J_{0}$
and
$J_{0}$
and
![]() $J_{1}$
agree on
$J_{1}$
agree on
![]() $\mathbb {C}_{\delta _{k-1}}$
(recall that
$\mathbb {C}_{\delta _{k-1}}$
(recall that
![]() $\delta _{k-1}<\delta _{k-2}$
) but are mutually generic afterward. Since
$\delta _{k-1}<\delta _{k-2}$
) but are mutually generic afterward. Since
![]() $H^*$
is guided by the collapse at
$H^*$
is guided by the collapse at
![]() $\kappa $
, both
$\kappa $
, both
![]() $J_0$
and
$J_0$
and
![]() $J_1$
are guided by the collapse at
$J_1$
are guided by the collapse at
![]() $\kappa $
. Hence, our inductive assumption implies that for each
$\kappa $
. Hence, our inductive assumption implies that for each
![]() $i\in 2$
,
$i\in 2$
,
![]() $\pi ^{-1}_{M_\kappa [G^*]}[J_i]$
has a sup
$\pi ^{-1}_{M_\kappa [G^*]}[J_i]$
has a sup
![]() $r_i$
in
$r_i$
in
![]() $j(\mathbb {C}_\rho (\vec {\delta }\upharpoonright k-1))$
. By the agreement between
$j(\mathbb {C}_\rho (\vec {\delta }\upharpoonright k-1))$
. By the agreement between
![]() $J_0$
and
$J_0$
and
![]() $J_1$
up to stage
$J_1$
up to stage
![]() $\delta _{k-1}<\delta _{k-2}$
, we know that
$\delta _{k-1}<\delta _{k-2}$
, we know that
![]() $r_{0}\upharpoonright j(\mathbb {C}_{\delta _{k-1}})=r_{1}\upharpoonright j(\mathbb {C}_{\delta _{k-1}})$
. We let
$r_{0}\upharpoonright j(\mathbb {C}_{\delta _{k-1}})=r_{1}\upharpoonright j(\mathbb {C}_{\delta _{k-1}})$
. We let
![]() $\bar {r}$
denote the common value. Finally, we define
$\bar {r}$
denote the common value. Finally, we define
![]() $r^*$
to be the function
$r^*$
to be the function
![]() $\bar {r}\,^\frown \langle r_i\upharpoonright j(\mathbb {C}_\rho (\vec {\delta }\upharpoonright k-1)):i<2\rangle $
. Then
$\bar {r}\,^\frown \langle r_i\upharpoonright j(\mathbb {C}_\rho (\vec {\delta }\upharpoonright k-1)):i<2\rangle $
. Then
![]() $r^*$
is a condition in
$r^*$
is a condition in
![]() $j(\mathbb {C}_\rho (\vec {\delta }))$
which is a sup of
$j(\mathbb {C}_\rho (\vec {\delta }))$
which is a sup of
![]() $\pi ^{-1}_{M_\kappa [G^*]}[H^*]$
.
$\pi ^{-1}_{M_\kappa [G^*]}[H^*]$
.
This completes the inductive step and the proof of the proposition.▪
6.2 No new branches
In this subsection, we will show that various
![]() ${\mathcal {F}}$
-completely proper posets do not add branches through Aronszajn trees of interest. We will use this general result to show, in particular, that tails of the club adding poset
${\mathcal {F}}$
-completely proper posets do not add branches through Aronszajn trees of interest. We will use this general result to show, in particular, that tails of the club adding poset
![]() $\mathbb {C}_\rho $
do not add any branches to trees
$\mathbb {C}_\rho $
do not add any branches to trees
![]() $\dot {T}$
which are Aronszajn trees in an intermediate extension obtained by forcing with
$\dot {T}$
which are Aronszajn trees in an intermediate extension obtained by forcing with
![]() $\mathbb {C}_\sigma {\ast \dot {\mathbb {S}}_\sigma }$
, for
$\mathbb {C}_\sigma {\ast \dot {\mathbb {S}}_\sigma }$
, for
![]() $\sigma <\rho $
. This will ensure that the tree specializing iteration of length
$\sigma <\rho $
. This will ensure that the tree specializing iteration of length
![]() $\rho $
above is in fact an iteration of specializing Aronszajn trees in the extension by
$\rho $
above is in fact an iteration of specializing Aronszajn trees in the extension by
![]() $\mathbb {C}_\rho $
, a conclusion which is essential in order to see that the specializing iteration does not collapse
$\mathbb {C}_\rho $
, a conclusion which is essential in order to see that the specializing iteration does not collapse
![]() $\kappa $
.
$\kappa $
.
Arguments for securing that certain posets do not add new cofinal branches to trees play a crucial role in consistency results concerning the tree property, going back to the work of Mitchell [Reference Mitchell34], and Magidor and Shelah [Reference Magidor and Shelah32]. Lemma 6 of Unger [Reference Unger41] provides such an argument with respect to closed posets and trees named by posets with reasonable chain condition, given constraints on the continuum function. Here, we prove a version of these results, in which the relevant posets (which in practice are variants of the club-adding poset) are
![]() $\mathcal {F}$
-completely proper (and thus
$\mathcal {F}$
-completely proper (and thus
![]() $\kappa $
-distributive) but not
$\kappa $
-distributive) but not
![]() $\kappa $
-closed.
$\kappa $
-closed.
The statement of the following proposition involves (names of) posets
![]() $\dot {\mathbb {Q}}_1,\dot {\mathbb {Q}}_2$
, and
$\dot {\mathbb {Q}}_1,\dot {\mathbb {Q}}_2$
, and
![]() $\dot {\mathbb {S}}$
. To relate the statement to our scenario, we suggest keeping in mind the following assignments of the posets: Fixing
$\dot {\mathbb {S}}$
. To relate the statement to our scenario, we suggest keeping in mind the following assignments of the posets: Fixing
![]() $\rho <\rho ^*< \kappa ^+$
,
$\rho <\rho ^*< \kappa ^+$
,
![]() $\dot {\mathbb {Q}}_1 = \dot {\mathbb {C}}_\rho $
is the
$\dot {\mathbb {Q}}_1 = \dot {\mathbb {C}}_\rho $
is the
![]() $(\mathbb {P}$
-name) of the first
$(\mathbb {P}$
-name) of the first
![]() $\rho $
steps of the club adding iteration,
$\rho $
steps of the club adding iteration,
![]() $\dot {\mathbb {S}} = \dot {\mathbb {S}}_\rho $
is the
$\dot {\mathbb {S}} = \dot {\mathbb {S}}_\rho $
is the
![]() $\mathbb {P}* \dot {\mathbb {C}}_\rho $
-name of the first
$\mathbb {P}* \dot {\mathbb {C}}_\rho $
-name of the first
![]() $\rho $
steps of the iteration specializing trees, and
$\rho $
steps of the iteration specializing trees, and
![]() $\dot {\mathbb {Q}}_2 = \dot {\mathbb {C}}_{[\rho ,\rho ^*)}$
is the
$\dot {\mathbb {Q}}_2 = \dot {\mathbb {C}}_{[\rho ,\rho ^*)}$
is the
![]() $\mathbb {P}* \dot {\mathbb {C}}_\rho $
-name of the segment of the final iteration from (and including) stage
$\mathbb {P}* \dot {\mathbb {C}}_\rho $
-name of the segment of the final iteration from (and including) stage
![]() $\rho $
to stage
$\rho $
to stage
![]() $\rho ^*$
(i.e.,
$\rho ^*$
(i.e.,
![]() $\dot {\mathbb {Q}}_1 * \dot {\mathbb {Q}}_2 = \dot {\mathbb {C}}_{\rho ^*}$
).
$\dot {\mathbb {Q}}_1 * \dot {\mathbb {Q}}_2 = \dot {\mathbb {C}}_{\rho ^*}$
).
Proposition 6.2 Suppose that
![]() $\dot {\mathbb {Q}}_1$
is a
$\dot {\mathbb {Q}}_1$
is a
![]() $\mathbb {P}$
-name and that
$\mathbb {P}$
-name and that
![]() $\dot {\mathbb {Q}}_2$
and
$\dot {\mathbb {Q}}_2$
and
![]() $\dot {\mathbb {S}}$
are
$\dot {\mathbb {S}}$
are
![]() $(\mathbb {P}\ast \dot {\mathbb {Q}}_1)$
-names so that
$(\mathbb {P}\ast \dot {\mathbb {Q}}_1)$
-names so that
![]() $\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}^2_2$
is
$\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}^2_2$
is
![]() ${\mathcal {F}}$
-completely proper and so that
${\mathcal {F}}$
-completely proper and so that
![]() $\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}^2_2$
forces that
$\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}^2_2$
forces that
![]() $\dot {\mathbb {S}}$
is
$\dot {\mathbb {S}}$
is
![]() $\kappa $
-c.c. Let
$\kappa $
-c.c. Let
![]() $\dot {T}$
be a
$\dot {T}$
be a
![]() $(\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast \dot {\mathbb {S}})$
-name for an Aronszajn tree on
$(\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast \dot {\mathbb {S}})$
-name for an Aronszajn tree on
![]() $\kappa $
. Then
$\kappa $
. Then
![]() $\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast (\dot {\mathbb {Q}}_2\times \dot {\mathbb {S}})$
forces that
$\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast (\dot {\mathbb {Q}}_2\times \dot {\mathbb {S}})$
forces that
![]() $\dot {T}$
is an Aronszajn tree.
$\dot {T}$
is an Aronszajn tree.
That is to say, forcing with
![]() $\dot {\mathbb {Q}}_2$
after
$\dot {\mathbb {Q}}_2$
after
![]() $\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast \dot {\mathbb {S}}$
does not add branches to
$\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast \dot {\mathbb {S}}$
does not add branches to
![]() $\dot {T}$
. To show this, we will follow the standard approach and show that if
$\dot {T}$
. To show this, we will follow the standard approach and show that if
![]() $\dot {\mathbb {Q}}_2$
were to add such a branch, then we can find some model in which a level of the tree has too many nodes.
$\dot {\mathbb {Q}}_2$
were to add such a branch, then we can find some model in which a level of the tree has too many nodes.
For the rest of this subsection, we suppose for a contradiction that
![]() $\dot {b}$
is
$\dot {b}$
is
![]() $(\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast (\dot {\mathbb {Q}}_2\times \dot {\mathbb {S}}))$
-name for a branch through
$(\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast (\dot {\mathbb {Q}}_2\times \dot {\mathbb {S}}))$
-name for a branch through
![]() $\dot {T}$
, where
$\dot {T}$
, where
![]() $\dot {T}$
is a
$\dot {T}$
is a
![]() $(\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast \dot {\mathbb {S}})$
-name for an Aronszajn tree on
$(\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast \dot {\mathbb {S}})$
-name for an Aronszajn tree on
![]() $\kappa $
. In the context of working with the forcing
$\kappa $
. In the context of working with the forcing
![]() $\mathbb {R}^*:=\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast (\dot {\mathbb {Q}}^2_2\times \dot {\mathbb {S}})$
, for which a typical generic looks like
$\mathbb {R}^*:=\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast (\dot {\mathbb {Q}}^2_2\times \dot {\mathbb {S}})$
, for which a typical generic looks like
![]() $G\ast Q_1\ast (Q_2^L\times Q_2^R\times F)$
, we will use
$G\ast Q_1\ast (Q_2^L\times Q_2^R\times F)$
, we will use
![]() $\dot {b}_L$
to denote the
$\dot {b}_L$
to denote the
![]() $(\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast (\dot {\mathbb {Q}}_2\times \dot {\mathbb {S}}))$
-name for
$(\mathbb {P}\ast \dot {\mathbb {Q}}_1\ast (\dot {\mathbb {Q}}_2\times \dot {\mathbb {S}}))$
-name for
![]() $\dot {b}[\dot {G}\ast {\dot {Q}}_1\ast (\dot {Q}_2^L\times \dot {F})]$
, i.e., the interpretation of
$\dot {b}[\dot {G}\ast {\dot {Q}}_1\ast (\dot {Q}_2^L\times \dot {F})]$
, i.e., the interpretation of
![]() $\dot {b}$
using the left generic filter added by
$\dot {b}$
using the left generic filter added by
![]() $\dot {\mathbb {Q}}^2_2$
.
$\dot {\mathbb {Q}}^2_2$
.
![]() $\dot {b}_R$
is defined similarly.
$\dot {b}_R$
is defined similarly.
The next lemma will be used as a successor step in obtaining a tree of conditions forcing incompatible information about a branch.
Lemma 6.3 (Under the assumptions of Proposition 6.2)
![]() $\mathbb {P}$
forces that for each
$\mathbb {P}$
forces that for each
![]() $\dot {\mathbb {Q}}_1$
-name
$\dot {\mathbb {Q}}_1$
-name
![]() $\dot {d}$
for a condition in
$\dot {d}$
for a condition in
![]() $\dot {\mathbb {Q}}_2$
, there is a dense, open set of c in
$\dot {\mathbb {Q}}_2$
, there is a dense, open set of c in
![]() $\dot {\mathbb {Q}}_1$
satisfying the following property: there exist names
$\dot {\mathbb {Q}}_1$
satisfying the following property: there exist names
![]() $\dot {d}_L,\dot {d}_R$
for conditions in
$\dot {d}_L,\dot {d}_R$
for conditions in
![]() $\dot {\mathbb {Q}}_2$
and an ordinal
$\dot {\mathbb {Q}}_2$
and an ordinal
![]() $\xi <\kappa $
so that:
$\xi <\kappa $
so that:
-
(1)
 $c\Vdash \dot {d}_Z\geq \dot {d}$
for each
$c\Vdash \dot {d}_Z\geq \dot {d}$
for each
 $Z\in \left \{ L,R\right \}$
; and
$Z\in \left \{ L,R\right \}$
; and -
(2)
 $\langle c,\dot {d}_L,\dot {d}_R,0_{\dot {\mathbb {S}}}\rangle \Vdash ^{V[\dot {G}]}_{\dot {\mathbb {Q}}_1\ast (\dot {\mathbb {Q}}_2\times \dot {\mathbb {Q}}_2\times \dot {\mathbb {S}})}\dot {b}_L(\xi )\neq \dot {b}_R(\xi )$
.
$\langle c,\dot {d}_L,\dot {d}_R,0_{\dot {\mathbb {S}}}\rangle \Vdash ^{V[\dot {G}]}_{\dot {\mathbb {Q}}_1\ast (\dot {\mathbb {Q}}_2\times \dot {\mathbb {Q}}_2\times \dot {\mathbb {S}})}\dot {b}_L(\xi )\neq \dot {b}_R(\xi )$
.
Proof We work in
![]() $V[G]$
. Fix
$V[G]$
. Fix
![]() $c\in \mathbb {Q}_1$
and a
$c\in \mathbb {Q}_1$
and a
![]() $\mathbb {Q}_1$
-name
$\mathbb {Q}_1$
-name
![]() $\dot {d}$
for a condition in
$\dot {d}$
for a condition in
![]() $\dot {\mathbb {Q}}_2$
. Let
$\dot {\mathbb {Q}}_2$
. Let
![]() $Q_1$
be
$Q_1$
be
![]() $V[G]$
-generic over
$V[G]$
-generic over
![]() $\mathbb {Q}_1$
containing c, and let
$\mathbb {Q}_1$
containing c, and let
![]() $Q_2^L\times Q_2^R$
be
$Q_2^L\times Q_2^R$
be
![]() $V[G\ast Q_1]$
-generic over
$V[G\ast Q_1]$
-generic over
![]() $\mathbb {Q}_2^2$
containing
$\mathbb {Q}_2^2$
containing
![]() $(d,d)$
.
$(d,d)$
.
We first claim that
![]() $0_{\mathbb {S}}$
forces over
$0_{\mathbb {S}}$
forces over
![]() $V[G\ast Q_1\ast (Q_2^L\times Q_2^R)]$
that
$V[G\ast Q_1\ast (Q_2^L\times Q_2^R)]$
that
![]() $\dot {b}_L\neq \dot {b}_R$
. Thus, let F be an arbitrary
$\dot {b}_L\neq \dot {b}_R$
. Thus, let F be an arbitrary
![]() $V[G\ast Q_1\ast (Q_2^L\times Q_2^R)]$
-generic filter for
$V[G\ast Q_1\ast (Q_2^L\times Q_2^R)]$
-generic filter for
![]() $\mathbb {S}$
. Since
$\mathbb {S}$
. Since
![]() $\mathbb {S}$
and
$\mathbb {S}$
and
![]() $\mathbb {Q}_2^2$
both live in
$\mathbb {Q}_2^2$
both live in
![]() $V[G\ast Q_1]$
, the product lemma implies that
$V[G\ast Q_1]$
, the product lemma implies that
![]() $Q_2^L\times Q_2^R$
is
$Q_2^L\times Q_2^R$
is
![]() $V[G\ast Q_1\ast F]$
-generic over
$V[G\ast Q_1\ast F]$
-generic over
![]() $\mathbb {Q}_2^2$
. Since
$\mathbb {Q}_2^2$
. Since
![]() $Q_2^L$
and
$Q_2^L$
and
![]() $Q_2^R$
are mutually
$Q_2^R$
are mutually
![]() $V[G\ast Q_1\ast F]$
-generic filters over
$V[G\ast Q_1\ast F]$
-generic filters over
![]() $\mathbb {Q}_2$
, we conclude that
$\mathbb {Q}_2$
, we conclude that
Therefore, if
![]() $b:=b_L=b_R$
, then b is in
$b:=b_L=b_R$
, then b is in
![]() $V[G\ast Q_1\ast F]$
, and therefore T is not an Aronszajn tree in that model, a contradiction.
$V[G\ast Q_1\ast F]$
, and therefore T is not an Aronszajn tree in that model, a contradiction.
We now claim that there is an ordinal
![]() $\xi $
so that
$\xi $
so that
![]() $0_{\mathbb {S}}$
forces over
$0_{\mathbb {S}}$
forces over
![]() $V[G\ast Q_1\ast (Q_2^L\times Q_2^R)]$
that
$V[G\ast Q_1\ast (Q_2^L\times Q_2^R)]$
that
![]() $\dot {b}_L(\xi )\neq \dot {b}_R(\xi )$
. Let
$\dot {b}_L(\xi )\neq \dot {b}_R(\xi )$
. Let
![]() $A\subseteq \mathbb {S}$
be a maximal antichain in
$A\subseteq \mathbb {S}$
be a maximal antichain in
![]() $V[G\ast Q_1\ast (Q_2^L\times Q_2^R)]$
consisting of conditions
$V[G\ast Q_1\ast (Q_2^L\times Q_2^R)]$
consisting of conditions
![]() $g\in \mathbb {S}$
so that for some
$g\in \mathbb {S}$
so that for some
![]() $\zeta _g<\kappa $
,
$\zeta _g<\kappa $
,
Because
![]() $\dot {b}_L$
and
$\dot {b}_L$
and
![]() $\dot {b}_R$
name branches in
$\dot {b}_R$
name branches in
![]() $\dot {T}$
, we see that for any
$\dot {T}$
, we see that for any
![]() $g\in A$
and
$g\in A$
and
![]() $\zeta \geq \zeta _g$
, g forces that
$\zeta \geq \zeta _g$
, g forces that
![]() $\dot {b}_L(\zeta )\neq \dot {b}_R(\zeta )$
. Since
$\dot {b}_L(\zeta )\neq \dot {b}_R(\zeta )$
. Since
![]() $\mathbb {S}$
is still
$\mathbb {S}$
is still
![]() $\kappa $
-c.c. after forcing to add
$\kappa $
-c.c. after forcing to add
![]() $Q_2^L\times Q_2^R$
, we know that A has size
$Q_2^L\times Q_2^R$
, we know that A has size
![]() $<\kappa $
in
$<\kappa $
in
![]() $V[G\ast Q_1\ast (Q_2^L\times Q_2^R)]$
. Therefore, letting
$V[G\ast Q_1\ast (Q_2^L\times Q_2^R)]$
. Therefore, letting
![]() $\xi :=\sup _{g\in A}\zeta _g$
,
$\xi :=\sup _{g\in A}\zeta _g$
,
![]() $\xi <\kappa $
. Then
$\xi <\kappa $
. Then
![]() $\xi $
witnesses the claim: indeed, if
$\xi $
witnesses the claim: indeed, if
![]() $f\in \mathbb {S}$
is any condition, we may extend it to
$f\in \mathbb {S}$
is any condition, we may extend it to
![]() $f^*$
so that
$f^*$
so that
![]() $f^*$
is above some
$f^*$
is above some
![]() $g\in A$
. By the remarks above and since
$g\in A$
. By the remarks above and since
![]() $\xi \geq \zeta _g$
, we know that
$\xi \geq \zeta _g$
, we know that
![]() $f^*\Vdash \dot {b}_L(\xi )\neq \dot {b}_R(\xi )$
, completing the proof of the second claim.
$f^*\Vdash \dot {b}_L(\xi )\neq \dot {b}_R(\xi )$
, completing the proof of the second claim.
Since
![]() $(c,\dot {d},\dot {d})\in Q_1\ast (Q_2^L\times Q_2^R)$
, we may find an extension
$(c,\dot {d},\dot {d})\in Q_1\ast (Q_2^L\times Q_2^R)$
, we may find an extension
![]() $(c^*,\dot {d}_L,\dot {d}_R)$
of
$(c^*,\dot {d}_L,\dot {d}_R)$
of
![]() $(c,\dot {d},\dot {d})$
as well as an ordinal
$(c,\dot {d},\dot {d})$
as well as an ordinal
![]() $\xi <\kappa $
so that
$\xi <\kappa $
so that
![]() $(c^*,\dot {d}_L,\dot {d}_R)$
forces that
$(c^*,\dot {d}_L,\dot {d}_R)$
forces that
![]() $0_{\dot {\mathbb {S}}}$
forces that
$0_{\dot {\mathbb {S}}}$
forces that
![]() $\dot {b}_L(\xi )\neq \dot {b}_R(\xi )$
. Then
$\dot {b}_L(\xi )\neq \dot {b}_R(\xi )$
. Then
![]() $c^*\geq c$
is in the desired dense set.▪
$c^*\geq c$
is in the desired dense set.▪
For the rest of the subsection, let
![]() $\vec {M}=\langle M_\alpha :\alpha \in B\rangle $
be a sequence which is suitable with respect to all parameters of interest. Since
$\vec {M}=\langle M_\alpha :\alpha \in B\rangle $
be a sequence which is suitable with respect to all parameters of interest. Since
![]() $\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}^2_2$
is
$\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}^2_2$
is
![]() $\mathcal {F}$
-completely proper, which implies that
$\mathcal {F}$
-completely proper, which implies that
![]() $\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}_2$
is
$\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}_2$
is
![]() $\mathcal {F}$
-completely proper, we may assume that
$\mathcal {F}$
-completely proper, we may assume that
![]() $\operatorname {dom}(\vec {M})$
satisfies the conclusion of Definition 5.3 with respect to
$\operatorname {dom}(\vec {M})$
satisfies the conclusion of Definition 5.3 with respect to
![]() $\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}^2_2$
and with respect to
$\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}^2_2$
and with respect to
![]() $\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}_2$
.
$\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}_2$
.
Fix
![]() $M^*\prec H(\kappa ^{++})$
, where
$M^*\prec H(\kappa ^{++})$
, where
![]() $M^*$
has size
$M^*$
has size
![]() $\kappa $
, is closed under
$\kappa $
, is closed under
![]() $< \kappa $
-sequences, and contains
$< \kappa $
-sequences, and contains
![]() $\vec {M}$
as well as
$\vec {M}$
as well as
![]() $\lhd $
from Notation 2.6 as an element. Let M denote the transitive collapse of
$\lhd $
from Notation 2.6 as an element. Let M denote the transitive collapse of
![]() $M^*$
, so that M is a
$M^*$
, so that M is a
![]() $\kappa $
-model. Since
$\kappa $
-model. Since
![]() $\operatorname {dom}(\vec {M})\in \mathcal {F}^+$
, we may find an M-normal ultrafilter U so that, letting
$\operatorname {dom}(\vec {M})\in \mathcal {F}^+$
, we may find an M-normal ultrafilter U so that, letting
![]() $j:M\longrightarrow N$
be the associated ultrapower map,
$j:M\longrightarrow N$
be the associated ultrapower map,
![]() $\kappa \in j(\operatorname {dom}(\vec {M}))$
. As usual, we use
$\kappa \in j(\operatorname {dom}(\vec {M}))$
. As usual, we use
![]() $M_\kappa $
to denote
$M_\kappa $
to denote
![]() $j(\vec {M})(\kappa )$
. The following claim shows that we can build the desired tree of conditions forcing incompatible information about the branch.
$j(\vec {M})(\kappa )$
. The following claim shows that we can build the desired tree of conditions forcing incompatible information about the branch.
Claim 6.2
![]() $j(\mathbb {P})$
forces over N that there exist sequences
$j(\mathbb {P})$
forces over N that there exist sequences
![]() $\langle \dot {c}_\nu :\nu <\omega _1\rangle $
and
$\langle \dot {c}_\nu :\nu <\omega _1\rangle $
and
![]() $\langle \dot {d}_s:s\in 2^{<\omega _1}\rangle $
so that the following properties hold:
$\langle \dot {d}_s:s\in 2^{<\omega _1}\rangle $
so that the following properties hold:
-
(1) for each
 $f\in (2^{\omega _1})^{N[\dot {G}_{j(\mathbb {P})}]}$
,
$f\in (2^{\omega _1})^{N[\dot {G}_{j(\mathbb {P})}]}$
,
 $\langle (\dot {c}_\nu ,\dot {d}_{f\upharpoonright \nu }):\nu <\omega _1\rangle $
is an increasing sequence of conditions in
$\langle (\dot {c}_\nu ,\dot {d}_{f\upharpoonright \nu }):\nu <\omega _1\rangle $
is an increasing sequence of conditions in
 $\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}_2$
which is guided by the collapse at
$\dot {\mathbb {Q}}_1\ast \dot {\mathbb {Q}}_2$
which is guided by the collapse at
 $\kappa $
(see Definition 5.2); and
$\kappa $
(see Definition 5.2); and -
(2) if
 $s\neq t$
are in
$s\neq t$
are in
 $2^\nu $
for some
$2^\nu $
for some
 $\nu <\omega _1$
, then
$\nu <\omega _1$
, then  $$ \begin{align*}j(\langle \dot{c}_\nu,\dot{d}_s,\dot{d}_t,0_{\dot{\mathbb{S}}}\rangle)\Vdash^{N[\dot{G}_{j(\mathbb{P})}]}_{j\left(\dot{\mathbb{Q}}_1\ast(\dot{\mathbb{Q}}_2\times\dot{\mathbb{Q}}_2\times\dot{\mathbb{S}})\right)} j(\dot{b})_L\upharpoonright\kappa\neq j(\dot{b})_R\upharpoonright\kappa. \end{align*} $$
$$ \begin{align*}j(\langle \dot{c}_\nu,\dot{d}_s,\dot{d}_t,0_{\dot{\mathbb{S}}}\rangle)\Vdash^{N[\dot{G}_{j(\mathbb{P})}]}_{j\left(\dot{\mathbb{Q}}_1\ast(\dot{\mathbb{Q}}_2\times\dot{\mathbb{Q}}_2\times\dot{\mathbb{S}})\right)} j(\dot{b})_L\upharpoonright\kappa\neq j(\dot{b})_R\upharpoonright\kappa. \end{align*} $$
Proof The definition is by recursion. Let
![]() $G^*$
be an arbitrary V-generic over
$G^*$
be an arbitrary V-generic over
![]() $j(\mathbb {P})$
, and let
$j(\mathbb {P})$
, and let
![]() $G=G^*\cap \mathbb {P}$
. Let
$G=G^*\cap \mathbb {P}$
. Let
![]() $(c_0,\dot {d}_0)$
be the trivial condition in
$(c_0,\dot {d}_0)$
be the trivial condition in
![]() $\mathbb {Q}_1\ast \dot {\mathbb {Q}}_2$
. In order to show that the desired sequences generate filters which are guided by the collapse at
$\mathbb {Q}_1\ast \dot {\mathbb {Q}}_2$
. In order to show that the desired sequences generate filters which are guided by the collapse at
![]() $\kappa $
(which in turn will guarantee that they have upper bounds), we will show that (1)–(3) of Lemma 5.5 are satisfied. In particular, to secure (3) of that lemma, throughout the construction, we will select objects which are minimal according to the fixed well-order
$\kappa $
(which in turn will guarantee that they have upper bounds), we will show that (1)–(3) of Lemma 5.5 are satisfied. In particular, to secure (3) of that lemma, throughout the construction, we will select objects which are minimal according to the fixed well-order
![]() $\lhd $
of
$\lhd $
of
![]() $H(\kappa ^+)$
. We remark that the entire construction takes place in
$H(\kappa ^+)$
. We remark that the entire construction takes place in
![]() $N[G^*]$
, but the proper initial segments can be carried out in
$N[G^*]$
, but the proper initial segments can be carried out in
![]() $M[G]$
using a proper initial segment of
$M[G]$
using a proper initial segment of
![]() $f_\kappa $
, the standard surjection from
$f_\kappa $
, the standard surjection from
![]() $\kappa $
onto
$\kappa $
onto
![]() $\omega _1$
added by
$\omega _1$
added by
![]() $G^*$
.
$G^*$
.
Suppose that
![]() $\nu $
is a limit and that for all
$\nu $
is a limit and that for all
![]() $\mu <\nu $
and all
$\mu <\nu $
and all
![]() $s\in 2^\mu $
, we have defined
$s\in 2^\mu $
, we have defined
![]() $c_\mu $
and
$c_\mu $
and
![]() $\dot {d}_s$
. Then we let
$\dot {d}_s$
. Then we let
![]() $\dot {c}_\nu $
be the
$\dot {c}_\nu $
be the
![]() $\lhd $
-least
$\lhd $
-least
![]() $\mathbb {P}$
-name for a condition in
$\mathbb {P}$
-name for a condition in
![]() $\dot {\mathbb {Q}}_1$
so that
$\dot {\mathbb {Q}}_1$
so that
![]() $c_\nu :=\dot {c}_\nu [G]$
is a sup of
$c_\nu :=\dot {c}_\nu [G]$
is a sup of
![]() $\langle c_\mu :\mu <\nu \rangle $
. Similarly, for
$\langle c_\mu :\mu <\nu \rangle $
. Similarly, for
![]() $s\in 2^\nu $
, we let
$s\in 2^\nu $
, we let
![]() $\dot {d}_s$
be a
$\dot {d}_s$
be a
![]() $\mathbb {Q}_1$
-name forced to be a sup of
$\mathbb {Q}_1$
-name forced to be a sup of
![]() $\langle \dot {d}_{s\upharpoonright \mu }:\mu <\nu \rangle $
so that a
$\langle \dot {d}_{s\upharpoonright \mu }:\mu <\nu \rangle $
so that a
![]() $\mathbb {P}$
-name for
$\mathbb {P}$
-name for
![]() $\dot {d}_s$
is
$\dot {d}_s$
is
![]() $\lhd $
-minimal. Note that item (2) in the claim still holds since if
$\lhd $
-minimal. Note that item (2) in the claim still holds since if
![]() $s\neq t$
are in
$s\neq t$
are in
![]() $2^\nu $
, then there exists some
$2^\nu $
, then there exists some
![]() $\mu <\nu $
so that
$\mu <\nu $
so that
![]() $s\upharpoonright \mu \neq t\upharpoonright \mu $
. So
$s\upharpoonright \mu \neq t\upharpoonright \mu $
. So
![]() $j(\langle c_\mu ,\dot {d}_{s\upharpoonright \mu },\dot {d}_{t\upharpoonright \mu },0_{\dot {\mathbb {S}}}\rangle )$
forces that
$j(\langle c_\mu ,\dot {d}_{s\upharpoonright \mu },\dot {d}_{t\upharpoonright \mu },0_{\dot {\mathbb {S}}}\rangle )$
forces that
![]() $j(\dot {b})_L\upharpoonright \kappa \neq j(\dot {b})_R\upharpoonright \kappa $
. Hence, the extension
$j(\dot {b})_L\upharpoonright \kappa \neq j(\dot {b})_R\upharpoonright \kappa $
. Hence, the extension
![]() $j(\langle c_\nu ,\dot {d}_s,\dot {d}_t,0_{\dot {\mathbb {S}}}\rangle )$
also forces this.
$j(\langle c_\nu ,\dot {d}_s,\dot {d}_t,0_{\dot {\mathbb {S}}}\rangle )$
also forces this.
Now we consider the successor step. Suppose that we have defined
![]() $c_\nu $
and
$c_\nu $
and
![]() $\dot {d}_s$
for all
$\dot {d}_s$
for all
![]() $s\in 2^\nu $
. In order to ensure that the assumptions of Lemma 5.5 are satisfied, and thereby ensure that the sequences are guided by the collapse at
$s\in 2^\nu $
. In order to ensure that the assumptions of Lemma 5.5 are satisfied, and thereby ensure that the sequences are guided by the collapse at
![]() $\kappa $
(which in turn will guarantee they have an upper bound), we will first define an auxiliary extension
$\kappa $
(which in turn will guarantee they have an upper bound), we will first define an auxiliary extension
![]() $c^*_\nu \geq c_\nu $
and for each
$c^*_\nu \geq c_\nu $
and for each
![]() $s\in 2^\nu $
, a
$s\in 2^\nu $
, a
![]() $\mathbb {Q}_1$
-name
$\mathbb {Q}_1$
-name
![]() $\dot {d}^*_s$
forced by
$\dot {d}^*_s$
forced by
![]() $c^*_\nu $
to extend
$c^*_\nu $
to extend
![]() $\dot {d}_s$
. Toward this end, let
$\dot {d}_s$
. Toward this end, let
![]() $\gamma :=f_\kappa (\nu )$
, where
$\gamma :=f_\kappa (\nu )$
, where
![]() $f_\kappa $
is the standard surjection added by
$f_\kappa $
is the standard surjection added by
![]() $G^*$
from
$G^*$
from
![]() $\omega _1$
onto
$\omega _1$
onto
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $u_\gamma $
be the
$u_\gamma $
be the
![]() $\gamma $
th condition in
$\gamma $
th condition in
![]() $\mathbb {Q}_1 \ast \dot {\mathbb {Q}}_2$
, and write
$\mathbb {Q}_1 \ast \dot {\mathbb {Q}}_2$
, and write
![]() $u_\gamma $
as
$u_\gamma $
as
![]() $\langle c^\gamma ,\dot {d}^\gamma \rangle $
. If
$\langle c^\gamma ,\dot {d}^\gamma \rangle $
. If
![]() $c^\gamma $
does not extend
$c^\gamma $
does not extend
![]() $c_\nu $
in
$c_\nu $
in
![]() $\mathbb {Q}_1$
, set
$\mathbb {Q}_1$
, set
![]() $c^*_\nu =c_\nu $
and
$c^*_\nu =c_\nu $
and
![]() $\dot {d}^*_s=\dot {d}_s$
. On the other hand, if
$\dot {d}^*_s=\dot {d}_s$
. On the other hand, if
![]() $c^\gamma \geq c_\nu $
, we set
$c^\gamma \geq c_\nu $
, we set
![]() $c^*_\nu =c^\gamma $
. Then, given
$c^*_\nu =c^\gamma $
. Then, given
![]() $s\in 2^\nu $
, if
$s\in 2^\nu $
, if
![]() $c^*_\nu \Vdash \dot {d}^\gamma \geq \dot {d}_s$
, we set
$c^*_\nu \Vdash \dot {d}^\gamma \geq \dot {d}_s$
, we set
![]() $\dot {d}^*_s=\dot {d}^\gamma $
, and otherwise we set
$\dot {d}^*_s=\dot {d}^\gamma $
, and otherwise we set
![]() $\dot {d}^*_s=\dot {d}_s$
. Note that there is at most one s that falls into the first of these, since
$\dot {d}^*_s=\dot {d}_s$
. Note that there is at most one s that falls into the first of these, since
![]() $c^*_\nu \Vdash \left \{\dot {d}_s:s\in 2^\nu \right \}$
is an antichain in
$c^*_\nu \Vdash \left \{\dot {d}_s:s\in 2^\nu \right \}$
is an antichain in
![]() $\dot {\mathbb {Q}}_2$
.
$\dot {\mathbb {Q}}_2$
.
Now, we move to defining
![]() $c_{\nu +1}$
and
$c_{\nu +1}$
and
![]() $\dot {d}_t$
for all
$\dot {d}_t$
for all
![]() $t\in 2^{\nu +1}$
. By Lemma 6.3, for each
$t\in 2^{\nu +1}$
. By Lemma 6.3, for each
![]() $s\in 2^\nu $
, the set
$s\in 2^\nu $
, the set
![]() $D_s$
of all
$D_s$
of all
![]() $c\in {\mathbb {Q}_1}$
for which there exist names
$c\in {\mathbb {Q}_1}$
for which there exist names
![]() $\dot {d}_L$
and
$\dot {d}_L$
and
![]() $\dot {d}_R$
and an ordinal
$\dot {d}_R$
and an ordinal
![]() $\xi <\kappa $
satisfying
$\xi <\kappa $
satisfying
-
(i)
 $c\Vdash \dot {d}_Z\geq \dot {d}_s$
for each
$c\Vdash \dot {d}_Z\geq \dot {d}_s$
for each
 $Z\in \left \{ L,R\right \}$
; and
$Z\in \left \{ L,R\right \}$
; and -
(ii)
 $\langle c,\dot {d}_L,\dot {d}_R,0_{\dot {\mathbb {S}}}\rangle \Vdash {\dot {b}_L(\xi )\neq \dot {b}_R(\xi )}$
$\langle c,\dot {d}_L,\dot {d}_R,0_{\dot {\mathbb {S}}}\rangle \Vdash {\dot {b}_L(\xi )\neq \dot {b}_R(\xi )}$
is dense, open in
![]() $\mathbb {Q}_{1}$
. By Lemma 5.6 applied to
$\mathbb {Q}_{1}$
. By Lemma 5.6 applied to
![]() $\mathbb {Q}_1$
, there exists an extension of
$\mathbb {Q}_1$
, there exists an extension of
![]() $c_\nu $
inside
$c_\nu $
inside
![]() $\bigcap _{s\in 2^\nu }D_s$
. Let
$\bigcap _{s\in 2^\nu }D_s$
. Let
![]() $\dot {c}_{\nu +1}$
be the
$\dot {c}_{\nu +1}$
be the
![]() $\lhd $
-minimal
$\lhd $
-minimal
![]() $\mathbb {P}$
-name so that
$\mathbb {P}$
-name so that
![]() $c_{\nu +1}:=\dot {c}_{\nu +1}[G]$
is such an extension. For each
$c_{\nu +1}:=\dot {c}_{\nu +1}[G]$
is such an extension. For each
![]() $s\in 2^\nu $
, we may find an ordinal
$s\in 2^\nu $
, we may find an ordinal
![]() $\xi _s<\kappa $
and
$\xi _s<\kappa $
and
![]() $\mathbb {Q}_1$
-names
$\mathbb {Q}_1$
-names
![]() $\dot {d}_{s^\frown \langle 0\rangle }$
and
$\dot {d}_{s^\frown \langle 0\rangle }$
and
![]() $\dot {d}_{s^\frown \langle 1\rangle }$
so that
$\dot {d}_{s^\frown \langle 1\rangle }$
so that
![]() $c_{\nu +1}\Vdash \dot {d}_{s^\frown \langle i\rangle }\geq \dot {d}_s$
, so that
$c_{\nu +1}\Vdash \dot {d}_{s^\frown \langle i\rangle }\geq \dot {d}_s$
, so that
![]() $\langle c_{\nu +1},\dot {d}_{s^\frown \langle 0\rangle },\dot {d}_{s^\frown \langle 1\rangle },0_{\dot {\mathbb {S}}}\rangle $
forces that
$\langle c_{\nu +1},\dot {d}_{s^\frown \langle 0\rangle },\dot {d}_{s^\frown \langle 1\rangle },0_{\dot {\mathbb {S}}}\rangle $
forces that
![]() $\dot {b}_L(\xi _s)\neq \dot {b}_R(\xi _s)$
, and so that
$\dot {b}_L(\xi _s)\neq \dot {b}_R(\xi _s)$
, and so that
![]() $\mathbb {P}$
-names for
$\mathbb {P}$
-names for
![]() $\dot {d}_{s^\frown \langle 0\rangle }$
and
$\dot {d}_{s^\frown \langle 0\rangle }$
and
![]() $\dot {d}_{s^\frown \langle 1\rangle }$
are
$\dot {d}_{s^\frown \langle 1\rangle }$
are
![]() $\lhd $
-minimal. Applying j to this statement, we secure (2) of the claim. This completes the proof.▪
$\lhd $
-minimal. Applying j to this statement, we secure (2) of the claim. This completes the proof.▪
Now that we have proved the above claim, we can finish the proof of Proposition 6.2.
Proof of Proposition 6.2.
Let
![]() $G^*$
be N-generic over
$G^*$
be N-generic over
![]() $j(\mathbb {P})$
, let
$j(\mathbb {P})$
, let
![]() $G:=G^*\cap \mathbb {P}$
, and fix sequences
$G:=G^*\cap \mathbb {P}$
, and fix sequences
![]() $\langle c^{{0}}_\nu :\nu <\omega _1\rangle $
and
$\langle c^{{0}}_\nu :\nu <\omega _1\rangle $
and
![]() $\langle \dot {d}^{{0}}_s:s\in 2^{<\omega _1}\rangle $
satisfying Claim 6.2. Let
$\langle \dot {d}^{{0}}_s:s\in 2^{<\omega _1}\rangle $
satisfying Claim 6.2. Let
![]() $\langle c_\nu :\nu <\omega _1\rangle $
and
$\langle c_\nu :\nu <\omega _1\rangle $
and
![]() $\langle \dot {d}_s:s\in 2^{<\omega _1}\rangle $
denote the sequences of their j-images. For each
$\langle \dot {d}_s:s\in 2^{<\omega _1}\rangle $
denote the sequences of their j-images. For each
![]() $f\in (2^{\omega _1})^{N[G^*]}$
,
$f\in (2^{\omega _1})^{N[G^*]}$
,
![]() $\langle {(c^0_\nu ,\dot {d}^0_{f\upharpoonright \nu })}:\nu <\omega _1\rangle $
is guided by the collapse at
$\langle {(c^0_\nu ,\dot {d}^0_{f\upharpoonright \nu })}:\nu <\omega _1\rangle $
is guided by the collapse at
![]() $\kappa $
. Moreover,
$\kappa $
. Moreover,
![]() $\operatorname {dom}(\vec {M})$
satisfies Definition 5.3, and
$\operatorname {dom}(\vec {M})$
satisfies Definition 5.3, and
![]() $\kappa \in j(\operatorname {dom}(\vec {M}))$
. Since
$\kappa \in j(\operatorname {dom}(\vec {M}))$
. Since
![]() $j(\mathbb {Q}_1\ast \dot {\mathbb {Q}}_2)$
is
$j(\mathbb {Q}_1\ast \dot {\mathbb {Q}}_2)$
is
![]() $j(\mathcal {F})$
-completely proper, we may find a condition
$j(\mathcal {F})$
-completely proper, we may find a condition
![]() $(c^*,\dot {d}_f)$
which is a sup in
$(c^*,\dot {d}_f)$
which is a sup in
![]() $j(\mathbb {Q}_1\ast \dot {\mathbb {Q}}_2)$
of
$j(\mathbb {Q}_1\ast \dot {\mathbb {Q}}_2)$
of
![]() $\langle (c_\nu ,\dot {d}_{f\upharpoonright \nu }):\nu <\omega _1\rangle $
(note that
$\langle (c_\nu ,\dot {d}_{f\upharpoonright \nu }):\nu <\omega _1\rangle $
(note that
![]() $c^*$
is independent of f since any two sups are
$c^*$
is independent of f since any two sups are
![]() $=^*$
-equal). By item (2) of the previous claim, we know that if
$=^*$
-equal). By item (2) of the previous claim, we know that if
![]() $f\neq g$
are in
$f\neq g$
are in
![]() $(2^{\omega _1})\cap N[G^*]$
, then
$(2^{\omega _1})\cap N[G^*]$
, then
![]() $\langle c^*,\dot {d}_f,\dot {d}_g,0_{j(\dot {\mathbb {S}})}\rangle $
forces that
$\langle c^*,\dot {d}_f,\dot {d}_g,0_{j(\dot {\mathbb {S}})}\rangle $
forces that
![]() $j(\dot {b})_L\upharpoonright \kappa \neq j(\dot {b})_R\upharpoonright \kappa $
.
$j(\dot {b})_L\upharpoonright \kappa \neq j(\dot {b})_R\upharpoonright \kappa $
.
Now, let
![]() $Q_1^*\ast F^*$
be
$Q_1^*\ast F^*$
be
![]() $N[G^*]$
-generic over
$N[G^*]$
-generic over
![]() $j(\mathbb {Q}_1\ast \dot {\mathbb {S}})$
with
$j(\mathbb {Q}_1\ast \dot {\mathbb {S}})$
with
![]() $Q_1^*$
containing
$Q_1^*$
containing
![]() $c^*$
. Applying item (2) of the previous claim again, we know that if
$c^*$
. Applying item (2) of the previous claim again, we know that if
![]() $f\neq g$
are in
$f\neq g$
are in
![]() $(2^{\omega _1})\cap N[G^*]$
, then
$(2^{\omega _1})\cap N[G^*]$
, then
![]() $\langle d_f,d_g\rangle $
forces in
$\langle d_f,d_g\rangle $
forces in
![]() $j(\mathbb {Q}^2_2)$
that
$j(\mathbb {Q}^2_2)$
that
![]() $j(\dot {b})_L\upharpoonright \kappa \neq j(\dot {b})_R\upharpoonright \kappa $
. We note here that the tree of interest, namely
$j(\dot {b})_L\upharpoonright \kappa \neq j(\dot {b})_R\upharpoonright \kappa $
. We note here that the tree of interest, namely
![]() $T^*:=j(\dot {T})[G^*\ast Q_1^*\ast F^*]$
, is a member of
$T^*:=j(\dot {T})[G^*\ast Q_1^*\ast F^*]$
, is a member of
![]() $N[G^*\ast Q_1^*\ast F^*]$
, i.e., exists prior to forcing with
$N[G^*\ast Q_1^*\ast F^*]$
, i.e., exists prior to forcing with
![]() $j(\mathbb {Q}_2^2)$
.
$j(\mathbb {Q}_2^2)$
.
For each
![]() $f\in (2^{\omega _1})\cap N[G^*]$
, let
$f\in (2^{\omega _1})\cap N[G^*]$
, let
![]() $d^*_f$
be an extension of
$d^*_f$
be an extension of
![]() $d_f$
in
$d_f$
in
![]() $j(\mathbb {Q}_2)$
which decides the value of
$j(\mathbb {Q}_2)$
which decides the value of
![]() $j(\dot {b})(\kappa )$
, say as
$j(\dot {b})(\kappa )$
, say as
![]() $\alpha _f$
. We claim that if
$\alpha _f$
. We claim that if
![]() $f\neq g$
are in
$f\neq g$
are in
![]() $(2^{\omega _1})\cap N[G^*]$
, then
$(2^{\omega _1})\cap N[G^*]$
, then
![]() $\alpha _f\neq \alpha _g$
. Indeed, suppose for a contradiction that there were
$\alpha _f\neq \alpha _g$
. Indeed, suppose for a contradiction that there were
![]() $f\neq g$
with
$f\neq g$
with
![]() $\alpha _f=\alpha _g$
. Then force in
$\alpha _f=\alpha _g$
. Then force in
![]() $j(\mathbb {Q}^2_2)$
above the condition
$j(\mathbb {Q}^2_2)$
above the condition
![]() $\langle d^*_f,d^*_g\rangle $
to obtain a pair
$\langle d^*_f,d^*_g\rangle $
to obtain a pair
![]() $\bar {Q}_2^L\times \bar {Q}_2^R$
of mutually generic filters for
$\bar {Q}_2^L\times \bar {Q}_2^R$
of mutually generic filters for
![]() $j(\mathbb {Q}_2)$
. Since
$j(\mathbb {Q}_2)$
. Since
![]() $\alpha _f=\alpha _g$
, the branch of
$\alpha _f=\alpha _g$
, the branch of
![]() $T^*$
below
$T^*$
below
![]() $\alpha _f$
is the same as the branch of
$\alpha _f$
is the same as the branch of
![]() $T^*$
below
$T^*$
below
![]() $\alpha _g$
. However, the branch of
$\alpha _g$
. However, the branch of
![]() $T^*$
below
$T^*$
below
![]() $\alpha _f$
equals
$\alpha _f$
equals
![]() $(j(\dot {b})[\bar {Q}_2^L])\upharpoonright \kappa $
and the branch of
$(j(\dot {b})[\bar {Q}_2^L])\upharpoonright \kappa $
and the branch of
![]() $T^*$
below
$T^*$
below
![]() $\alpha _g$
equals
$\alpha _g$
equals
![]() $(j(\dot {b})[\bar {Q}_2^R])\upharpoonright \kappa $
, contradicting the fact that
$(j(\dot {b})[\bar {Q}_2^R])\upharpoonright \kappa $
, contradicting the fact that
![]() $\langle d^*_f,d^*_g\rangle $
forces that the interpretations diverge below
$\langle d^*_f,d^*_g\rangle $
forces that the interpretations diverge below
![]() $\kappa $
.
$\kappa $
.
Since
![]() $(2^{\omega _1})\cap N[G^*]$
has size
$(2^{\omega _1})\cap N[G^*]$
has size
![]() $j(\kappa )$
in
$j(\kappa )$
in
![]() $N[G^*]$
and
$N[G^*]$
and
![]() $j(\mathbb {Q}_2\ast \dot {\mathbb {S}})$
preserves
$j(\mathbb {Q}_2\ast \dot {\mathbb {S}})$
preserves
![]() $j(\kappa )$
, this set still has size
$j(\kappa )$
, this set still has size
![]() $j(\kappa )$
in
$j(\kappa )$
in
![]() $N[G^*\ast Q_1^*\ast F^*]$
. Thus, in the model
$N[G^*\ast Q_1^*\ast F^*]$
. Thus, in the model
![]() $N[G^*\ast Q_1^*\ast F^*]$
, the function taking
$N[G^*\ast Q_1^*\ast F^*]$
, the function taking
![]() $f\in (2^{\omega _1})\cap N[G^*]$
to
$f\in (2^{\omega _1})\cap N[G^*]$
to
![]() $\alpha _f$
is an injection. Therefore, level
$\alpha _f$
is an injection. Therefore, level
![]() $\kappa $
of
$\kappa $
of
![]() $T^*$
has size
$T^*$
has size
![]() $j(\kappa )$
, which contradicts the fact that
$j(\kappa )$
, which contradicts the fact that
![]() $j(\kappa )$
is
$j(\kappa )$
is
![]() $\aleph _2$
in
$\aleph _2$
in
![]() $N[G^*\ast Q_1^*\ast F^*]$
and that
$N[G^*\ast Q_1^*\ast F^*]$
and that
![]() $T^*$
is an Aronszajn tree on
$T^*$
is an Aronszajn tree on
![]() $j(\kappa )$
.▪
$j(\kappa )$
.▪
7 Putting it all together
Up to this point in the paper, we have worked to establish a number of isolated results. In this section, we will now define the poset which will witness Theorem 1.1. Each of the previous sections will function as a component in the inductive verification that this poset has the desired properties.
We recall that
![]() $\mathbb {P}$
denotes
$\mathbb {P}$
denotes
![]() $\operatorname {Col}(\omega _1,<\kappa )$
, the Levy collapse of the ineffable cardinal
$\operatorname {Col}(\omega _1,<\kappa )$
, the Levy collapse of the ineffable cardinal
![]() $\kappa $
. We define a
$\kappa $
. We define a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {\mathbb {C}}_{\kappa ^+}$
for a
$\dot {\mathbb {C}}_{\kappa ^+}$
for a
![]() $\kappa ^+$
-length iteration adding clubs, and we also define a
$\kappa ^+$
-length iteration adding clubs, and we also define a
![]() $(\mathbb {P}\ast \dot {\mathbb {C}}_{\kappa ^+})$
-name
$(\mathbb {P}\ast \dot {\mathbb {C}}_{\kappa ^+})$
-name
![]() $\dot {\mathbb {S}}_{\kappa ^+}$
for an iteration which specializes Aronszajn trees. This is done in such a way that for all
$\dot {\mathbb {S}}_{\kappa ^+}$
for an iteration which specializes Aronszajn trees. This is done in such a way that for all
![]() $\rho <\kappa ^+$
, the
$\rho <\kappa ^+$
, the
![]() $(\mathbb {P}\ast \dot {\mathbb {C}}_{\kappa ^+})$
-name
$(\mathbb {P}\ast \dot {\mathbb {C}}_{\kappa ^+})$
-name
![]() $\dot {\mathbb {S}}_\rho $
for the first
$\dot {\mathbb {S}}_\rho $
for the first
![]() $\rho $
-stages of
$\rho $
-stages of
![]() $\dot {\mathbb {S}}_{\kappa ^+}$
is actually a
$\dot {\mathbb {S}}_{\kappa ^+}$
is actually a
![]() $(\mathbb {P}\ast \dot {\mathbb {C}}_\rho )$
-name.
$(\mathbb {P}\ast \dot {\mathbb {C}}_\rho )$
-name.
More precisely, we define by recursion on
![]() $\rho \leq \kappa ^+$
the names
$\rho \leq \kappa ^+$
the names
![]() $\dot {\mathbb {C}}_\rho $
and
$\dot {\mathbb {C}}_\rho $
and
![]() $\dot {\mathbb {S}}_\rho $
. Suppose that
$\dot {\mathbb {S}}_\rho $
. Suppose that
![]() $\rho =\rho _0+1$
is a successor and that
$\rho =\rho _0+1$
is a successor and that
![]() $\dot {\mathbb {C}}_{\rho _0}$
and
$\dot {\mathbb {C}}_{\rho _0}$
and
![]() $\dot {\mathbb {S}}_{\rho _0}$
are both defined. Using the fixed well-order
$\dot {\mathbb {S}}_{\rho _0}$
are both defined. Using the fixed well-order
![]() $\lhd $
from Notation 2.6 as a bookkeeping device, we select a
$\lhd $
from Notation 2.6 as a bookkeeping device, we select a
![]() $(\mathbb {P}\ast \dot {\mathbb {C}}_{\rho _0}\ast \dot {\mathbb {S}}_{\rho _0})$
-name
$(\mathbb {P}\ast \dot {\mathbb {C}}_{\rho _0}\ast \dot {\mathbb {S}}_{\rho _0})$
-name
![]() $\dot {S}_{\rho _0}$
for a stationary subset of
$\dot {S}_{\rho _0}$
for a stationary subset of
![]() $\kappa \cap \operatorname {cof}(\omega )$
, and we define
$\kappa \cap \operatorname {cof}(\omega )$
, and we define
![]() $\dot {\mathbb {C}}_\rho :=\dot {\mathbb {C}}_{\rho _0}\ast \mathsf {CU}(\dot {S}_{\rho _0},\dot {\mathbb {S}}_{\rho _0})$
(see Definition 1.3). Next, we use
$\dot {\mathbb {C}}_\rho :=\dot {\mathbb {C}}_{\rho _0}\ast \mathsf {CU}(\dot {S}_{\rho _0},\dot {\mathbb {S}}_{\rho _0})$
(see Definition 1.3). Next, we use
![]() $\lhd $
to select a
$\lhd $
to select a
![]() $(\mathbb {P}\ast \dot {\mathbb {C}}_{\rho }\ast \dot {\mathbb {S}}_{\rho _0})$
-name
$(\mathbb {P}\ast \dot {\mathbb {C}}_{\rho }\ast \dot {\mathbb {S}}_{\rho _0})$
-name
![]() $\dot {T}_{\rho _0}$
for an Aronszajn tree on
$\dot {T}_{\rho _0}$
for an Aronszajn tree on
![]() $\kappa $
, and we set
$\kappa $
, and we set
![]() $\dot {\mathbb {S}}_\rho $
to be the
$\dot {\mathbb {S}}_\rho $
to be the
![]() $(\mathbb {P}\ast \dot {\mathbb {C}}_\rho )$
-name for
$(\mathbb {P}\ast \dot {\mathbb {C}}_\rho )$
-name for
![]() $\dot {\mathbb {S}}_{\rho _0}\ast \mathbb {S}(\dot {T}_{\rho _0})$
(see Definition 1.4).
$\dot {\mathbb {S}}_{\rho _0}\ast \mathbb {S}(\dot {T}_{\rho _0})$
(see Definition 1.4).
Now, suppose that
![]() $\rho $
is a limit and that we have defined the sequences
$\rho $
is a limit and that we have defined the sequences
![]() $\langle \dot {\mathbb {C}}_\xi ,\dot {\mathbb {C}}(\xi ):\xi <\rho \rangle $
and
$\langle \dot {\mathbb {C}}_\xi ,\dot {\mathbb {C}}(\xi ):\xi <\rho \rangle $
and
![]() $\langle \dot {\mathbb {S}}_\xi ,\dot {\mathbb {S}}(\xi ):\xi <\rho \rangle $
. We first let
$\langle \dot {\mathbb {S}}_\xi ,\dot {\mathbb {S}}(\xi ):\xi <\rho \rangle $
. We first let
![]() $\dot {\mathbb {C}}_\rho $
be the
$\dot {\mathbb {C}}_\rho $
be the
![]() $< \kappa $
-support limit of
$< \kappa $
-support limit of
![]() $\langle \dot {\mathbb {C}}_\xi ,\dot {\mathbb {C}}(\xi ):\xi <\rho \rangle $
. Second, we see that
$\langle \dot {\mathbb {C}}_\xi ,\dot {\mathbb {C}}(\xi ):\xi <\rho \rangle $
. Second, we see that
![]() $\mathbb {P}\ast \dot {\mathbb {C}}_\rho $
forces that
$\mathbb {P}\ast \dot {\mathbb {C}}_\rho $
forces that
![]() $\langle \dot {\mathbb {S}}_\xi ,\dot {\mathbb {S}}(\xi ):\xi <\rho \rangle $
names an iteration with countable support: by induction, if
$\langle \dot {\mathbb {S}}_\xi ,\dot {\mathbb {S}}(\xi ):\xi <\rho \rangle $
names an iteration with countable support: by induction, if
![]() $\xi <\rho $
is a limit, then
$\xi <\rho $
is a limit, then
![]() $\dot {\mathbb {S}}_\xi $
is the
$\dot {\mathbb {S}}_\xi $
is the
![]() $(\mathbb {P}\ast \dot {\mathbb {C}}_\xi )$
-name for the countable support limit of
$(\mathbb {P}\ast \dot {\mathbb {C}}_\xi )$
-name for the countable support limit of
![]() $\langle \dot {\mathbb {S}}_\zeta ,\dot {\mathbb {S}}(\zeta ):\zeta <\xi \rangle $
. However,
$\langle \dot {\mathbb {S}}_\zeta ,\dot {\mathbb {S}}(\zeta ):\zeta <\xi \rangle $
. However,
![]() $\dot {\mathbb {C}}_\rho $
is
$\dot {\mathbb {C}}_\rho $
is
![]() $\omega _1$
-closed, and consequently, the countable support limit of
$\omega _1$
-closed, and consequently, the countable support limit of
![]() $\langle \dot {\mathbb {S}}_\zeta ,\dot {\mathbb {S}}(\zeta ):\zeta <\xi \rangle $
is the same in both the extension by
$\langle \dot {\mathbb {S}}_\zeta ,\dot {\mathbb {S}}(\zeta ):\zeta <\xi \rangle $
is the same in both the extension by
![]() $\mathbb {P}\ast \dot {\mathbb {C}}_\xi $
and the extension by
$\mathbb {P}\ast \dot {\mathbb {C}}_\xi $
and the extension by
![]() $\mathbb {P}\ast \dot {\mathbb {C}}_\rho $
. In light of this, we let
$\mathbb {P}\ast \dot {\mathbb {C}}_\rho $
. In light of this, we let
![]() $\dot {\mathbb {S}}_\rho $
denote the countable support limit of
$\dot {\mathbb {S}}_\rho $
denote the countable support limit of
![]() $\langle \dot {\mathbb {S}}_\xi ,\dot {\mathbb {S}}(\xi ):\xi <\rho \rangle $
, noting that this is an
$\langle \dot {\mathbb {S}}_\xi ,\dot {\mathbb {S}}(\xi ):\xi <\rho \rangle $
, noting that this is an
![]() $\omega _1$
-closed poset in the extension by
$\omega _1$
-closed poset in the extension by
![]() $\mathbb {P}\ast \dot {\mathbb {C}}_\rho $
. This completes the definitions of the names. We may now define
$\mathbb {P}\ast \dot {\mathbb {C}}_\rho $
. This completes the definitions of the names. We may now define
![]() $\mathbb {R}^*:=\mathbb {P}\ast \dot {\mathbb {C}}_{\kappa ^+}\ast \dot {\mathbb {S}}_{\kappa ^+}$
.
$\mathbb {R}^*:=\mathbb {P}\ast \dot {\mathbb {C}}_{\kappa ^+}\ast \dot {\mathbb {S}}_{\kappa ^+}$
.
We begin our analysis of
![]() $\mathbb {R}^*$
with some simple remarks. First,
$\mathbb {R}^*$
with some simple remarks. First,
![]() $\mathbb {R}^*$
is
$\mathbb {R}^*$
is
![]() $\omega _1$
-closed, since all the posets under consideration are (and since our iterations were taken with supports which are at least countable). In addition,
$\omega _1$
-closed, since all the posets under consideration are (and since our iterations were taken with supports which are at least countable). In addition,
![]() $\mathbb {R}^*$
is
$\mathbb {R}^*$
is
![]() $\kappa ^+$
-c.c. Indeed,
$\kappa ^+$
-c.c. Indeed,
![]() $\mathbb {P}$
trivially is. Furthermore,
$\mathbb {P}$
trivially is. Furthermore,
![]() $\kappa ^{<\kappa }=\kappa $
after forcing with
$\kappa ^{<\kappa }=\kappa $
after forcing with
![]() $\mathbb {P}$
, and so if
$\mathbb {P}$
, and so if
![]() $\beta <\kappa ^+$
,
$\beta <\kappa ^+$
,
![]() $\dot {\mathbb {C}}_\beta $
is forced to be a poset of size
$\dot {\mathbb {C}}_\beta $
is forced to be a poset of size
![]() $\kappa $
. Since direct limits in the iteration
$\kappa $
. Since direct limits in the iteration
![]() $\dot {\mathbb {C}}_{\kappa ^+}$
are taken at all stages in
$\dot {\mathbb {C}}_{\kappa ^+}$
are taken at all stages in
![]() $\kappa ^+\cap \operatorname {cof}(\kappa )$
, standard arguments (e.g., see [Reference Baumgartner and Mathias6]) show that
$\kappa ^+\cap \operatorname {cof}(\kappa )$
, standard arguments (e.g., see [Reference Baumgartner and Mathias6]) show that
![]() $\dot {\mathbb {C}}_{\kappa ^+}$
is
$\dot {\mathbb {C}}_{\kappa ^+}$
is
![]() $\kappa ^+$
-c.c. Finally, since for every
$\kappa ^+$
-c.c. Finally, since for every
![]() $\beta <\kappa ^+$
,
$\beta <\kappa ^+$
,
![]() $\dot {\mathbb {S}}_\beta $
is forced to have size
$\dot {\mathbb {S}}_\beta $
is forced to have size
![]() $\kappa $
by
$\kappa $
by
![]() $\mathbb {P}\ast \dot {\mathbb {C}}_{\kappa ^+}$
, and since
$\mathbb {P}\ast \dot {\mathbb {C}}_{\kappa ^+}$
, and since
![]() $\dot {\mathbb {S}}_{\kappa ^+}$
is taken with countable supports, a standard
$\dot {\mathbb {S}}_{\kappa ^+}$
is taken with countable supports, a standard
![]() $\Delta $
-System argument shows that
$\Delta $
-System argument shows that
![]() $\dot {\mathbb {S}}_{\kappa ^+}$
is
$\dot {\mathbb {S}}_{\kappa ^+}$
is
![]() $\kappa ^+$
-c.c.
$\kappa ^+$
-c.c.
We next claim that if
![]() $\mathbb {R}^*$
preserves
$\mathbb {R}^*$
preserves
![]() $\kappa $
, then it forces all Aronszajn trees on
$\kappa $
, then it forces all Aronszajn trees on
![]() $\kappa $
are special, that such trees exist, and that every stationary subset
$\kappa $
are special, that such trees exist, and that every stationary subset
![]() $S\subseteq \kappa \cap \operatorname {cof}(\omega )$
reflects on every ordinal of cofinality
$S\subseteq \kappa \cap \operatorname {cof}(\omega )$
reflects on every ordinal of cofinality
![]() $\omega _1$
in some closed unbounded subset on
$\omega _1$
in some closed unbounded subset on
![]() $\kappa $
. First, suppose that
$\kappa $
. First, suppose that
![]() $\dot {T}$
is an
$\dot {T}$
is an
![]() $\mathbb {R}^*$
-name for an Aronszajn tree on
$\mathbb {R}^*$
-name for an Aronszajn tree on
![]() $\kappa $
. Because
$\kappa $
. Because
![]() $\mathbb {R}^*$
is
$\mathbb {R}^*$
is
![]() $\kappa ^+$
-c.c.,
$\kappa ^+$
-c.c.,
![]() $\dot {T}$
is a
$\dot {T}$
is a
![]() $(\mathbb {P}*\dot {\mathbb {C}}_{\gamma }*\dot {\mathbb {S}}_{\gamma })$
-name for some
$(\mathbb {P}*\dot {\mathbb {C}}_{\gamma }*\dot {\mathbb {S}}_{\gamma })$
-name for some
![]() $\gamma <\kappa ^+$
, and hence names an Aronszajn tree in any extension between that given by
$\gamma <\kappa ^+$
, and hence names an Aronszajn tree in any extension between that given by
![]() $\mathbb {P}*\dot {\mathbb {C}}_{\gamma }*\dot {\mathbb {S}}_{\gamma }$
and the full
$\mathbb {P}*\dot {\mathbb {C}}_{\gamma }*\dot {\mathbb {S}}_{\gamma }$
and the full
![]() $\mathbb {R}^*$
-extension. By our bookkeeping device, there is some
$\mathbb {R}^*$
-extension. By our bookkeeping device, there is some
![]() $\delta \geq \gamma $
so that
$\delta \geq \gamma $
so that
![]() $\dot {\mathbb {S}}(\delta )$
is forced by
$\dot {\mathbb {S}}(\delta )$
is forced by
![]() $\mathbb {P}*\dot {\mathbb {C}}_{\delta +1}*\dot {\mathbb {S}}_{\delta }$
to equal
$\mathbb {P}*\dot {\mathbb {C}}_{\delta +1}*\dot {\mathbb {S}}_{\delta }$
to equal
![]() $\dot {\mathbb {S}}(\dot {T})$
. Hence,
$\dot {\mathbb {S}}(\dot {T})$
. Hence,
![]() $\mathbb {R}^*$
forces that
$\mathbb {R}^*$
forces that
![]() $\dot {T}$
is special. Similarly, if
$\dot {T}$
is special. Similarly, if
![]() $\dot {S}$
is an
$\dot {S}$
is an
![]() $\mathbb {R}^*$
-name for a stationary subset of
$\mathbb {R}^*$
-name for a stationary subset of
![]() $\kappa \cap \operatorname {cof}(\omega )$
, then there is some
$\kappa \cap \operatorname {cof}(\omega )$
, then there is some
![]() $\alpha <\kappa ^+$
so that
$\alpha <\kappa ^+$
so that
![]() $\dot {S}$
is a
$\dot {S}$
is a
![]() $(\mathbb {P}*\dot {\mathbb {C}}_{\alpha }*\dot {\mathbb {S}}_{\alpha })$
-name, and hence there is some
$(\mathbb {P}*\dot {\mathbb {C}}_{\alpha }*\dot {\mathbb {S}}_{\alpha })$
-name, and hence there is some
![]() $\beta \geq \alpha $
so that
$\beta \geq \alpha $
so that
![]() $\dot {\mathbb {C}}(\beta )$
is forced by
$\dot {\mathbb {C}}(\beta )$
is forced by
![]() $\mathbb {P}*\dot {\mathbb {C}}_{\beta }$
to equal
$\mathbb {P}*\dot {\mathbb {C}}_{\beta }$
to equal
![]() $\mathsf {CU}(\dot {S},\dot {\mathbb {S}}_\beta )$
. Thus, in the extension by
$\mathsf {CU}(\dot {S},\dot {\mathbb {S}}_\beta )$
. Thus, in the extension by
![]() $\mathbb {P}*\dot {\mathbb {C}}_{\beta +1}*\dot {\mathbb {S}}_{\beta }$
,
$\mathbb {P}*\dot {\mathbb {C}}_{\beta +1}*\dot {\mathbb {S}}_{\beta }$
,
![]() $\dot {S}$
reflects almost everywhere, and since the forcing to complete
$\dot {S}$
reflects almost everywhere, and since the forcing to complete
![]() $\mathbb {P}*\dot {\mathbb {C}}_{\beta +1}*\dot {\mathbb {S}}_{\beta }$
to
$\mathbb {P}*\dot {\mathbb {C}}_{\beta +1}*\dot {\mathbb {S}}_{\beta }$
to
![]() $\mathbb {R}^*$
is
$\mathbb {R}^*$
is
![]() $\omega _1$
-closed,
$\omega _1$
-closed,
![]() $\dot {S}$
still reflects almost everywhere in the full
$\dot {S}$
still reflects almost everywhere in the full
![]() $\mathbb {R}^*$
-extension.
$\mathbb {R}^*$
-extension.
As a result of the previous discussion, we see that in order to show that
![]() $\mathbb {R}^*$
witnesses Theorem 1.1, we need to prove that
$\mathbb {R}^*$
witnesses Theorem 1.1, we need to prove that
![]() $\mathbb {R}^*$
preserves
$\mathbb {R}^*$
preserves
![]() $\kappa $
. To achieve this, we verify that (i)
$\kappa $
. To achieve this, we verify that (i)
![]() $\mathbb {P}$
forces
$\mathbb {P}$
forces
![]() $\dot {\mathbb {C}}_{\kappa ^+}$
is
$\dot {\mathbb {C}}_{\kappa ^+}$
is
![]() $\kappa $
-distributive, and that (ii)
$\kappa $
-distributive, and that (ii)
![]() $\mathbb {P}* \dot {\mathbb {C}}_{\kappa ^+}$
forces that
$\mathbb {P}* \dot {\mathbb {C}}_{\kappa ^+}$
forces that
![]() $\dot {\mathbb {S}}_{\kappa ^+}$
is
$\dot {\mathbb {S}}_{\kappa ^+}$
is
![]() $\kappa $
-c.c.
$\kappa $
-c.c.
To this end, we consider the following simplifications. First, concerning (i), we note that since
![]() $\dot {\mathbb {C}}_{\kappa ^+}$
is forced to be
$\dot {\mathbb {C}}_{\kappa ^+}$
is forced to be
![]() $\kappa ^+$
-c.c, it is sufficient to verify that
$\kappa ^+$
-c.c, it is sufficient to verify that
![]() $\dot {\mathbb {C}}_\rho $
is forced to be
$\dot {\mathbb {C}}_\rho $
is forced to be
![]() $\kappa $
-distributive for all
$\kappa $
-distributive for all
![]() $\rho < \kappa ^+$
to show that (i) holds. We will use Lemma 5.6 to verify this, by proving that for every
$\rho < \kappa ^+$
to show that (i) holds. We will use Lemma 5.6 to verify this, by proving that for every
![]() $\rho <\kappa ^+$
,
$\rho <\kappa ^+$
,
![]() $\dot {\mathbb {C}}_\rho $
is
$\dot {\mathbb {C}}_\rho $
is
![]() $\mathcal {F}$
-completely proper.
$\mathcal {F}$
-completely proper.
Second, concerning (ii), since
![]() $\dot {\mathbb {S}}_{\kappa ^+}$
names a countable support iteration, any
$\dot {\mathbb {S}}_{\kappa ^+}$
names a countable support iteration, any
![]() $\kappa $
-sized antichain would witness that some proper initial segment
$\kappa $
-sized antichain would witness that some proper initial segment
![]() $\dot {\mathbb {S}}_{\gamma }$
is not
$\dot {\mathbb {S}}_{\gamma }$
is not
![]() $\kappa $
-c.c. Therefore, it is sufficient to verify that
$\kappa $
-c.c. Therefore, it is sufficient to verify that
![]() $\mathbb {P}*\dot {\mathbb {C}}_{\kappa ^+}$
forces
$\mathbb {P}*\dot {\mathbb {C}}_{\kappa ^+}$
forces
![]() $\dot {\mathbb {S}}_\gamma $
is
$\dot {\mathbb {S}}_\gamma $
is
![]() $\kappa $
-c.c for every
$\kappa $
-c.c for every
![]() $\gamma < \kappa ^+$
. However, as
$\gamma < \kappa ^+$
. However, as
![]() $\dot {\mathbb {C}}_{\kappa ^+}$
names a
$\dot {\mathbb {C}}_{\kappa ^+}$
names a
![]() $\kappa ^+$
-cc poset, every
$\kappa ^+$
-cc poset, every
![]() $(\mathbb {P}*\dot {\mathbb {C}}_{\kappa ^+})$
-name for a subset of
$(\mathbb {P}*\dot {\mathbb {C}}_{\kappa ^+})$
-name for a subset of
![]() $\dot {\mathbb {S}}_{\gamma }$
of size
$\dot {\mathbb {S}}_{\gamma }$
of size
![]() $\kappa $
is equivalent to a
$\kappa $
is equivalent to a
![]() $(\mathbb {P}*\dot {\mathbb {C}}_{\rho })$
-name, for some
$(\mathbb {P}*\dot {\mathbb {C}}_{\rho })$
-name, for some
![]() $\rho \geq \gamma $
. Clearly, if
$\rho \geq \gamma $
. Clearly, if
![]() $\mathbb {P}*\dot {\mathbb {C}}_{\rho }$
forces
$\mathbb {P}*\dot {\mathbb {C}}_{\rho }$
forces
![]() $\dot {\mathbb {S}}_{\gamma }$
fails to satisfy the
$\dot {\mathbb {S}}_{\gamma }$
fails to satisfy the
![]() $\kappa $
-c.c for some
$\kappa $
-c.c for some
![]() $\gamma \leq \rho $
, then it forces
$\gamma \leq \rho $
, then it forces
![]() $\dot {\mathbb {S}}_\rho $
is not
$\dot {\mathbb {S}}_\rho $
is not
![]() $\kappa $
-c.c. We conclude that (ii) follows from the assertion that for every
$\kappa $
-c.c. We conclude that (ii) follows from the assertion that for every
![]() $\rho < \kappa ^+$
,
$\rho < \kappa ^+$
,
![]() $\mathbb {P}*\dot {\mathbb {C}}_\rho $
forces that
$\mathbb {P}*\dot {\mathbb {C}}_\rho $
forces that
![]() $\dot {\mathbb {S}}_\rho $
is
$\dot {\mathbb {S}}_\rho $
is
![]() $\kappa $
-c.c.
$\kappa $
-c.c.
Combining the two simplifications, it remains to prove the next claim.
Claim 7.1 The following holds for every
![]() $\rho <\kappa ^+$
:
$\rho <\kappa ^+$
:
-
(1)
 $\dot {\mathbb {C}}_\rho $
is
$\dot {\mathbb {C}}_\rho $
is
 $\mathcal {F}$
-completely proper; and
$\mathcal {F}$
-completely proper; and -
(2)
 $\mathbb {P}*\dot {\mathbb {C}}_\rho $
forces
$\mathbb {P}*\dot {\mathbb {C}}_\rho $
forces
 $\dot {\mathbb {S}}_\rho $
is
$\dot {\mathbb {S}}_\rho $
is
 $\kappa $
-c.c.
$\kappa $
-c.c.
We prove the claim by induction on
![]() $\rho < \kappa ^+$
. Let
$\rho < \kappa ^+$
. Let
![]() $\rho < \kappa ^+$
, and suppose that the claim holds for every
$\rho < \kappa ^+$
, and suppose that the claim holds for every
![]() $\sigma < \rho $
. In particular, if
$\sigma < \rho $
. In particular, if
![]() $\sigma <\rho $
, then since
$\sigma <\rho $
, then since
![]() $\mathbb {P}\ast \dot {\mathbb {C}}_\sigma $
forces that
$\mathbb {P}\ast \dot {\mathbb {C}}_\sigma $
forces that
![]() $\dot {\mathbb {S}}_\sigma $
is a countable support iteration specializing trees and since (2) holds at
$\dot {\mathbb {S}}_\sigma $
is a countable support iteration specializing trees and since (2) holds at
![]() $\sigma $
, we must have that
$\sigma $
, we must have that
![]() $\mathbb {P}\ast \dot {\mathbb {C}}_\sigma $
forces that
$\mathbb {P}\ast \dot {\mathbb {C}}_\sigma $
forces that
![]() $\dot {\mathbb {S}}_\sigma $
is a countable support iteration specializing Aronszajn trees. Hence, we see that assumptions (1)–(4) from the beginning of Section 6 hold. Applying Proposition 6.1, it follows that
$\dot {\mathbb {S}}_\sigma $
is a countable support iteration specializing Aronszajn trees. Hence, we see that assumptions (1)–(4) from the beginning of Section 6 hold. Applying Proposition 6.1, it follows that
![]() $\dot {\mathbb {C}}_\rho $
is
$\dot {\mathbb {C}}_\rho $
is
![]() $\mathcal {F}$
-completely proper, and moreover, so is
$\mathcal {F}$
-completely proper, and moreover, so is
![]() $\mathbb {C}_{\rho }(\vec {\delta })$
for every finite, decreasing sequence
$\mathbb {C}_{\rho }(\vec {\delta })$
for every finite, decreasing sequence
![]() $\vec {\delta }$
of ordinals below
$\vec {\delta }$
of ordinals below
![]() $\rho $
. We use this to prove that (2) of the claim holds at
$\rho $
. We use this to prove that (2) of the claim holds at
![]() $\rho $
.
$\rho $
.
We aim to apply Corollary 3.13 to the
![]() $\mathcal {F}$
-strongly proper poset
$\mathcal {F}$
-strongly proper poset
![]() $\mathbb {P}^*:=\mathbb {P}\ast \dot {\mathbb {C}}_\rho $
, and to do so, we need to verify that for each
$\mathbb {P}^*:=\mathbb {P}\ast \dot {\mathbb {C}}_\rho $
, and to do so, we need to verify that for each
![]() $\sigma <\rho $
,
$\sigma <\rho $
,
![]() $\mathbb {P}^*\ast \dot {\mathbb {S}}_\sigma \Vdash \dot {T}_\sigma $
is an Aronszajn tree. This is where the doubling tail products come into play. Indeed, we consider a slightly more general statement, which would allow us to use Proposition 6.2. For each decreasing sequence
$\mathbb {P}^*\ast \dot {\mathbb {S}}_\sigma \Vdash \dot {T}_\sigma $
is an Aronszajn tree. This is where the doubling tail products come into play. Indeed, we consider a slightly more general statement, which would allow us to use Proposition 6.2. For each decreasing sequence
![]() $\vec {\delta } = \langle \delta _{0},\dots ,\delta _{n-1}\rangle $
in
$\vec {\delta } = \langle \delta _{0},\dots ,\delta _{n-1}\rangle $
in
![]() $\rho $
, we let
$\rho $
, we let
![]() $\star _\rho (\vec {\delta })$
be the statement that
$\star _\rho (\vec {\delta })$
be the statement that
![]() $\mathbb {P}*\dot {\mathbb {C}}_\rho (\vec {\delta })$
forces
$\mathbb {P}*\dot {\mathbb {C}}_\rho (\vec {\delta })$
forces
![]() $\dot {\mathbb {S}}_{\delta _{n-1}}$
is
$\dot {\mathbb {S}}_{\delta _{n-1}}$
is
![]() $\kappa $
-c.c. (note that if
$\kappa $
-c.c. (note that if
![]() $\vec {\delta } = \emptyset $
, then the statement holds vacuously). We prove by induction on the reverse lexicographic order
$\vec {\delta } = \emptyset $
, then the statement holds vacuously). We prove by induction on the reverse lexicographic order
![]() $<_{\operatorname {\mathrm {rLex}}}$
on
$<_{\operatorname {\mathrm {rLex}}}$
on
![]() $[\rho ]^{<\omega }_{\text {dec}}$
that
$[\rho ]^{<\omega }_{\text {dec}}$
that
![]() $\star _\rho (\vec {\delta })$
holds. The base case of the induction, where
$\star _\rho (\vec {\delta })$
holds. The base case of the induction, where
![]() $\vec {\delta } = \emptyset $
, trivially holds, as mentioned above. For the induction step, fix
$\vec {\delta } = \emptyset $
, trivially holds, as mentioned above. For the induction step, fix
![]() $\vec {\delta } = \langle \delta _{{0}},\dots ,\delta _{{n-1}}\rangle \in [\rho ]^{<\omega }_{\text {dec}}$
and suppose that
$\vec {\delta } = \langle \delta _{{0}},\dots ,\delta _{{n-1}}\rangle \in [\rho ]^{<\omega }_{\text {dec}}$
and suppose that
![]() $\star _\rho (\vec {\gamma })$
holds for every
$\star _\rho (\vec {\gamma })$
holds for every
![]() $\vec {\gamma } <_{\operatorname {\mathrm {rLex}}} \vec {\delta }$
. To show that
$\vec {\gamma } <_{\operatorname {\mathrm {rLex}}} \vec {\delta }$
. To show that
![]() $\star _\rho (\vec {\delta })$
holds, we need to verify that
$\star _\rho (\vec {\delta })$
holds, we need to verify that
![]() $\mathbb {P} * \dot {\mathbb {C}}_\rho (\vec {\delta })$
forces that
$\mathbb {P} * \dot {\mathbb {C}}_\rho (\vec {\delta })$
forces that
![]() $\dot {\mathbb {S}}_{\delta _{n-1}}$
is
$\dot {\mathbb {S}}_{\delta _{n-1}}$
is
![]() $\kappa $
-c.c. For this, in turn, by Corollary 3.13, it is sufficient to verify that for every
$\kappa $
-c.c. For this, in turn, by Corollary 3.13, it is sufficient to verify that for every
![]() $\gamma < \delta _{n-1}$
,
$\gamma < \delta _{n-1}$
,
![]() $\mathbb {P} * \dot {\mathbb {C}}_\rho (\vec {\delta })\ast \dot {\mathbb {S}}_\gamma $
forces that
$\mathbb {P} * \dot {\mathbb {C}}_\rho (\vec {\delta })\ast \dot {\mathbb {S}}_\gamma $
forces that
![]() $\dot {T}_\gamma $
is an Aronszajn tree on
$\dot {T}_\gamma $
is an Aronszajn tree on
![]() $\kappa $
. If
$\kappa $
. If
![]() $\delta _{n-1} = 0$
, there is nothing to prove. Otherwise, let
$\delta _{n-1} = 0$
, there is nothing to prove. Otherwise, let
![]() $\gamma < \delta _{n-1}$
, and set
$\gamma < \delta _{n-1}$
, and set
![]() $\vec {\gamma } := \vec {\delta }^\frown \langle \gamma \rangle $
. By Proposition 6.2 and the definition of
$\vec {\gamma } := \vec {\delta }^\frown \langle \gamma \rangle $
. By Proposition 6.2 and the definition of
![]() $\dot {\mathbb {C}}_\rho (\vec {\gamma })$
, it suffices to verify that
$\dot {\mathbb {C}}_\rho (\vec {\gamma })$
, it suffices to verify that
![]() $\mathbb {P} * \dot {\mathbb {C}}_\rho (\vec {\gamma })$
forces that
$\mathbb {P} * \dot {\mathbb {C}}_\rho (\vec {\gamma })$
forces that
![]() $\dot {\mathbb {S}}_\gamma $
is
$\dot {\mathbb {S}}_\gamma $
is
![]() $\kappa $
-c.c, to conclude that
$\kappa $
-c.c, to conclude that
![]() $\mathbb {P} * \dot {\mathbb {C}}_\rho (\vec {\delta })\ast \dot {\mathbb {S}}_\gamma $
forces that
$\mathbb {P} * \dot {\mathbb {C}}_\rho (\vec {\delta })\ast \dot {\mathbb {S}}_\gamma $
forces that
![]() $\dot {T}_\gamma $
is Aronszajn. However, the last is just
$\dot {T}_\gamma $
is Aronszajn. However, the last is just
![]() $\star _\rho (\vec {\gamma })$
, which holds by our inductive assumption and the fact that
$\star _\rho (\vec {\gamma })$
, which holds by our inductive assumption and the fact that
![]() $\vec {\gamma } <_{\operatorname {\mathrm {rLex}}} \vec {\delta }$
. This concludes the proof of Claim 7.1, which in turn finishes the proof of Theorem 1.1.
$\vec {\gamma } <_{\operatorname {\mathrm {rLex}}} \vec {\delta }$
. This concludes the proof of Claim 7.1, which in turn finishes the proof of Theorem 1.1.
We conclude the paper with two questions:
Question 7.2 Is an ineffable cardinal necessary for proving Theorem 1.1? Is a weakly compact cardinal sufficient?
As we have remarked throughout the paper, we only use ineffability in the proof of Proposition 3.12 (and thus in the corollaries of this proposition). If one could prove this proposition assuming only a weakly compact, then that would suffice to show that a weakly compact is optimal.
We also mention the following long-standing question.
Question 7.3 Is a weakly compact cardinal needed for
![]() $\mathsf {SATP}(\omega _2)+2^{\omega _1}=\omega _3$
?
$\mathsf {SATP}(\omega _2)+2^{\omega _1}=\omega _3$
?
We recall that in the Laver–Shelah model of
![]() $\mathsf {SATP}(\omega _2)$
,
$\mathsf {SATP}(\omega _2)$
,
![]() $2^{\omega _1}=\omega _3$
. Moreover, Rinot has shown [Reference Rinot36] that if the
$2^{\omega _1}=\omega _3$
. Moreover, Rinot has shown [Reference Rinot36] that if the
![]() $\mathsf {GCH}$
and
$\mathsf {GCH}$
and
![]() $\mathsf {SATP}(\omega _2)$
both hold, then
$\mathsf {SATP}(\omega _2)$
both hold, then
![]() $\omega _2$
is weakly compact in L.
$\omega _2$
is weakly compact in L.
Acknowledgment
The authors would like to thank Itay Neeman for helpful comments and corrections and the referee for a thorough reading of the manuscript and many valuable suggestions and comments.