Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-06-09T00:19:06.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Constructing Galois Representations with Very Large Image

Published online by Cambridge University Press:  20 November 2018

Ravi Ramakrishna
Ravi Ramakrishna*
Affiliation:
Department of Mathematics Cornell University Ithaca, NY 14853 U.S.A. e-mail: ravi@math.cornell.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Starting with a 2-dimensional mod 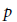$p$ Galois representation, we construct a deformation to a power series ring in infinitely many variables over the 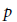$p$-adics. The image of this representation is full in the sense that it contains 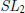$S{{L}_{2}}$ of this power series ring. Furthermore, all 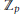${{\mathbb{Z}}_{p}}$ specializations of this deformation are potentially semistable at 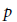$p$.

Keywords

11F80Galois representationdeformation.
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 1 , 01 February 2008 , pp. 208 - 221
Copyright
Copyright © Canadian Mathematical Society 2008

References

[B] Böckle, G., A local-to-global principle for deformations of Galois representations. J. Reine Angew. Math. 509(1999), 199–236.Google Scholar
[Bo] Boston, N., Appendix to On p-adic families of Galois representations, by A. Wiles and B. Mazur. Compositio Math. 59(1986), no. 2, 261–264.Google Scholar
[KLR1] Khare, C., Larsen, M., and Ramakrishna, R., Constructing semisimple p-adic Galois representations with prescribed properties. Amer. J. Math. 127(2005), no. 4, 709–734.Google Scholar
[KLR2] Khare, C., Transcendental ℓ-adic Galois representations. Math Res. Let. 12(2005), no. 5-6, 685–699.Google Scholar
[M1] Mazur, B., Deforming Galois representations. In: Galois Groups over Q. Math. Sci. Res. Inst. Publ. 16, Springer-Verlag, Berlin, 1989.Google Scholar
[M2] Mazur, B., An introduction to the deformation theory of Galois representations. In: Modular Forms and Fermat's Last Theorem. Springer, New York, 1997, pp. 243–311.Google Scholar
[NSW] Neukirch, J., Schmidt, A., and Wingberg, K., Cohomology of number fields, Grundlehren der MathematischenWissenschaften 323, Springer-Verlag, 2000.Google Scholar
[R1] Ramakrishna, R., Lifting Galois representations. Invent.Math. 138(1999), no. 3, 537–562.Google Scholar
[R2] Ramakrishna, R., Deforming Galois representations and the conjectures of Serre and Fontaine-Mazur. Ann. of Math. 156(2002), no. 1, 115–154.Google Scholar
[Ro1] Rohrlich, D., False division towers of elliptic curves. J. Algebra 229(2000), no. 1, 249–279.Google Scholar
[Ro2] Rohrlich, D., Modular units and the surjectivity of a Galois representation. J. Number Theory 107(2004), no. 1, 8–24.Google Scholar
[T] Taylor, R., On icosahedral Artin representations. II. Amer. J. Math. 125(2003), no. 3, 549–566.Google Scholar
[W] Wiles, A., Modular elliptic curves and Fermat's last theorem. Ann. of Math. 141(1995), no. 3, 443–551.Google Scholar