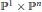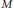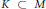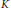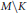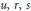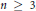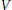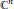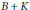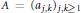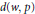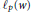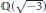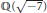Research Article
About the Defectivity of Certain Segre–Veronese Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-974
-
- Article
-
- You have access
- Export citation
Uniform Linear Bound in Chevalley’s Lemma
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 721-733
-
- Article
-
- You have access
- Export citation
Heegner Points and the Rank of Elliptic Curves over Large Extensions of Global Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-490
-
- Article
-
- You have access
- Export citation
Semi-Classical Wavefront Set and Fourier Integral Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-263
-
- Article
-
- You have access
- Export citation
Convex Bodies of Minimal Volume, Surface Area and Mean Width with Respect to Thin Shells
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-32
-
- Article
-
- You have access
- Export citation
Hölder Compactification for Some Manifolds with Pinched Negative Curvature Near Infinity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1201-1218
-
- Article
-
- You have access
- Export citation
CR Extension from Manifolds of Higher Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1219-1239
-
- Article
-
- You have access
- Export citation
A Multi-Frey Approach to Some Multi-Parameter Families of Diophantine Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 491-519
-
- Article
-
- You have access
- Export citation
Higher Order Tangents to Analytic Varieties along Curves. II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 33-63
-
- Article
-
- You have access
- Export citation
An AF Algebra Associated with the Farey Tessellation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 975-1000
-
- Article
-
- You have access
- Export citation
Correction
Erratum to: An Exactly Solved Model for Recombination, Mutation and Selection
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 264-265
-
- Article
-
- You have access
- Export citation
Research Article
Genus 2 Curves with Quaternionic Multiplication
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 734-757
-
- Article
-
- You have access
- Export citation
Categorification of the Colored Jones Polynomial and Rasmussen Invariant of Links
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1240-1266
-
- Article
-
- You have access
- Export citation
On the Hyperinvariant Subspace Problem. IV
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 758-789
-
- Article
-
- You have access
- Export citation
Invariants and Coinvariants of the Symmetric Group in Noncommuting Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 266-296
-
- Article
-
- You have access
- Export citation
Isometric Group Actions on Hilbert Spaces: Structure of Orbits
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1001-1009
-
- Article
-
- You have access
- Export citation
Classification of Linear Weighted Graphs up to Blowing-Up and Blowing-Down
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 64-87
-
- Article
-
- You have access
- Export citation
Matrices Whose Norms Are Determined by Their Actions on Decreasing Sequences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 520-531
-
- Article
-
- You have access
- Export citation
Nonadjacent Radix-τ Expansions of Integers in Euclidean Imaginary Quadratic Number Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1267-1282
-
- Article
-
- You have access
- Export citation
Local Bounds for Torsion Points on Abelian Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 532-555
-
- Article
-
- You have access
- Export citation