Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T13:00:41.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Contractive Representation Theory for the Unitary Group of C(X, M2)

Published online by Cambridge University Press:  20 November 2018

Alan L. T. Paterson
Alan L. T. Paterson*
Affiliation:
University of Aberdeen, Aberdeen, Scotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One motivation for studying representation theory for the unitary group 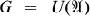of a unital C*-algebra 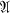arises from Theoretical Physics. (In the latter connection, Segal [9] and Arveson [1] have developed a representation theory for G. Their approach is in a different direction from ours.) Another motivation for studying the representation theory of G arises out of the desire to unify the theories of amenable von Neumann algebras and amenable locally compact groups.

A serious problem for such a representation theory is the absence of Haar measure on G in general.

In [7], the author introduced the class RepdG of contractive unitary representations of G, the strong metric condition involved compensating for the lack of Haar measure.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 3 , 01 June 1987 , pp. 612 - 624
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Arveson, W., Representations of unitary groups, Preprint.Google Scholar
2. Bourbaki, N., Lie groups and Lie algebras, Part 1 (Addison-Wesley, Reading, Mass., 1975).Google Scholar
3. de la Harpe, P., Moyennabilité du groupe unitaire et propriété P de Schwartz des algèbres de von Neumann in Algèbres d'opérateurs, Lecture Notes in Mathematics 725 (Springer-Verlag, Berlin, 1979), 220–227.Google Scholar
4. Fell, J. M. G., The structure of algebras of operator fields, Acta Math. 106 (1961), 233–280.Google Scholar
5. Massey, W. S., Algebraic topology: an introduction (Springer-Verlag, New York, 1967).Google Scholar
6. Naimark, M. A., Normed rings (Wolters-Noordhoff Publishing, Groningeen, 1970).Google Scholar
7. Paterson, A. L. T., Harmonic analysis on unitary groups, J. Functional Analysis 53 (1983), 203–223.Google Scholar
8. Robert, A., Introduction to the representation theory of compact and locally compact groups (Cambridge University Press, Cambridge, 1983).CrossRefGoogle Scholar
9. Segal, I., The structure of a class of representations of the unitary group on a Hilbert space, Proc. Amer. Math. Soc. 5 (1957), 197–203.Google Scholar
10. Sugiura, M., Unitary representations and harmonic analysis (Halsted Press, New York, 1975).Google Scholar
11. Switzer, R. M., Algebraic topology — homotopy and homology (Springer-Verlag, New York, 1975).CrossRefGoogle Scholar
12. Želobenko, D. P., Compact Lie groups and their representations (American Mathematical Society, Providence, 1973).CrossRefGoogle Scholar