Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Longyear, J.Q.
1981.
A survey of nested designs.
Journal of Statistical Planning and Inference,
Vol. 5,
Issue. 2,
p.
181.
Bush, K.A.
1981.
Families of regular designs based on geometries.
Journal of Statistical Planning and Inference,
Vol. 5,
Issue. 4,
p.
391.
Kageyama, Sanpei
and
Tanaka, Tatsuzo
1981.
Some families of group divisible designs.
Journal of Statistical Planning and Inference,
Vol. 5,
Issue. 3,
p.
231.
Street, Deborah J.
1984.
Some constructions for PBIBDs.
Journal of Statistical Planning and Inference,
Vol. 10,
Issue. 1,
p.
119.
Velazquez-Gutierrez, Juan M.
and
Vargas-Rosales, Cesar
2017.
Sequence Sets in Wireless Communication Systems: A Survey.
IEEE Communications Surveys & Tutorials,
Vol. 19,
Issue. 2,
p.
1225.
Hanaki, Akihide
Kharaghani, Hadi
Mohammadian, Ali
and
Tayfeh‐Rezaie, Behruz
2020.
Classification of skew‐Hadamard matrices of order 32 and association schemes of order 31.
Journal of Combinatorial Designs,
Vol. 28,
Issue. 6,
p.
421.

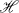 . A matrix
. A matrix 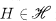 is of
is of 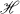 is
is 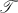 . A matrix P is a
. A matrix P is a 