Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brown, William C.
1980.
Multiplicity sequences and the modules of higher differentials.
Journal of Algebra,
Vol. 64,
Issue. 1,
p.
1.
Lipman, Joseph
and
Teissier, Bernard
1991.
The Unreal Life of Oscar Zariski.
p.
232.

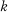 is algebraically closed and contained in
is algebraically closed and contained in 