Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-09T02:47:06.860Z Has data issue: false hasContentIssue false
  • English
  • Français

Discrete Series of Classical Groups

Published online by Cambridge University Press:  20 November 2018

Yuanli Zhang
Yuanli Zhang*
Affiliation:
Centre de recherches mathématiques, Case postale 6128, Succursale centre-ville, Montréal, QC, H3C 3J7 email: yz@math.purdue.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 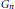${{G}_{n}}$ be the split classical groups 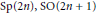$\text{Sp}(\text{2}n\text{),}\,\text{SO(2}n\text{+1})$ and 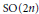$\text{SO(2}n\text{)}$ defined over a 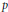$p$-adic field F or the quasi-split classical groups 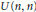$U(n,n)$ and 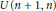$U(n+1,n)$ with respect to a quadratic extension 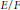$E/F$. We prove the self-duality of unitary supercuspidal data of standard Levi subgroups of 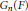${{G}_{n}}(F)$ which give discrete series representations of 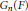${{G}_{n}}(F)$.

Keywords

22E35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 5 , 01 October 2000 , pp. 1101 - 1120
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Ban, D., Self-duality in the Case of SO(2n, F). Preprint.Google Scholar
[2] Bourbaki, N., Éléments de mathématique. Fasc. 52XIV, Groupes et algébres de Lie. Chapitres IV, V, VI. Actualit és Scientifiques et Industrielles 1337, Hermann, Paris, 1968.Google Scholar
[3] Casselman, W., Introduction to the Theory of Admissible Representations of p-adic Reductive Groups. Preprint.Google Scholar
[4] Casselman, W. and Shahidi, F., Irreducibility of StandardModules for Generic Representations. Ann. Sci. École Norm. Sup. 31(1998), 561–589.Google Scholar
[5] Goldberg, D., Reducibility of Induced Representations for Sp(2N) and SO(N). Amer. J. Math. 116(1994), 1101–1151.Google Scholar
[6] Jantzen, C., On Square-integrable Representations of Classical p-adic Groups. Preprint.Google Scholar
[7] Jacquet, H., Piateski-Shapiro, I. and Shalika, J., Rankin-Selberg Convolutions. Amer. J. Math. 105(1983), 367–464.Google Scholar
[8] Muić, G., Some results on square Integrable Representations; Irreducibility of Standard Representations. Internat. Math. Res. Notices 14(1998), 705–726.Google Scholar
[9] Shahidi, F., A Proof of Langlands’ Conjecture on PlancherelMeasures; Complementary Series for p-adic Groups. Ann. of Math. 132(1990), 273–330.Google Scholar
[10] Shahidi, F., On multiplicativity of local factors. In: Festschrift in Honor of I. I. Piateski-Shapiro, Part II, Israel Math. Conf. Proc. 3, Weizmann, Jerusalem, 1990, 279–289.Google Scholar
[11] Silberger, A., Introduction to Harmonic Analysis on p-Adic Groups. Math. Notes 23, Princeton University Press, Princeton, 1979.Google Scholar
[12] Silberger, A., Special Representations of Reductive p-Adic Groups are not integrable. Ann. of Math. 111(1980), 571–587.Google Scholar
[13] Silberger, A., Discrete Series of and Classification for p-adic Groups I. Amer. J. Math. (6) 103(1981), 1241–1321.Google Scholar
[14] Tadic, M., On Regular Square Integrable Representations of p-Adic Groups. Amer. J. Math. 120(1998), 159–210.Google Scholar
[15] Zhang, Z., L-packets and Reducibilities. J. Reine Angew. Math. 510(1999), 83–102.Google Scholar