Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-29T14:44:26.627Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimates for the Koebe Constant and the Second Coefficient for Some Classes of Univalent Functions

Published online by Cambridge University Press:  20 November 2018

D. Bshouty ,
W. Hengartner  and
G. Schober
D. Bshouty
Affiliation:
The Technion, Haifa, Israel
W. Hengartner
Affiliation:
Université Laval, Québec, Québec
G. Schober
Affiliation:
Indiana University, Bloomington, Indiana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S be the set of all normalized univalent analytic functions ƒ(z) = z + a2z2 + … in the open unit disk U. Then ƒ(U) contains the disk 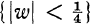. Here 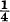is the best possible constant and is referred to as the Koebe constant for S. On the other extreme, ƒ(U) cannot contain the disk {|w| < 1}; unless ƒ is the identity mapping.

In order to interpolate between the class S and the identity mapping, one may introduce the families , of functions ƒ ∈ S such that ƒ(U) contains the disk {|w| < d};. Then S(d1) ⊃ S(d2) for d1 < d2,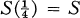 and S(1) contains only the identity mapping. It is obvious that d is the “Koebe constant” for S(d). The relation between d and the second coefficient a2 has been studied by E. Netanyahu [5, 6].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 6 , 01 December 1980 , pp. 1311 - 1324
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Baernstein, A. II, Integral means, univalent functions and circular symmetrization, Acta Math. 133 (1974), 139–169.Google Scholar
2. Jabotinsky, E., Analytic iteration, Trans. Amer. Math. Soc. 108 (1963), 457–477.Google Scholar
3. Jensen, E. and Waadeland, H., A coefficient inequality for bi-univalent functions, Det. Kgl. Norske Vidensk. Selsk, Skr. 15 (1972), 1–11.Google Scholar
4. Lewin, M., On a coefficient problem for bi-univalent functions, Proc. Amer. Math. Soc. 18 (1967), 63–68.Google Scholar
5. Netanyahu, E., The minimal distance of the image boundary from the origin and the second coefficient, Arch. Rational Mech. Anal. 32 (1969), 100–112.Google Scholar
6. Netanyahu, E., On univalent functions in the unit disk whose image contains a given disk, J. Analyse Math. 23 (1970), 305–322.Google Scholar
7. Smith, H. V., Bi-univalent polynomials, Simon Stevin 50 (1976-77), 115–122.Google Scholar