Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-08T17:52:41.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Euler-type Relative Equilibria and their Stability in Spaces of Constant Curvature

Published online by Cambridge University Press:  20 November 2018

Ernesto Pérez-Chavela  and
Juan Manuel Sánchez-Cerritos
Ernesto Pérez-Chavela
Affiliation:
Departamento de Matemáticas, Instituto Tecnológico Autónomo de México, México D.F., México e-mail: ernesto.perez@itam.mx
Juan Manuel Sánchez-Cerritos
Affiliation:
Departamento de Matemáticas, Universidad Autónoma Metropolitana - Iztapalapa, México D.F., México e-mail: sanchezj01@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider three point positive masses moving on 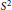${{S}^{2}}$ and 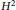${{H}^{2}}$. An Eulerian-relative equilibrium is a relative equilibrium where the three masses are on the same geodesic. In this paper we analyze the spectral stability of these kind of orbits where the mass at the middle is arbitrary and the masses at the ends are equal and located at the same distance from the central mass. For the case of 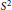${{S}^{2}}$, we found a positive measure set in the set of parameters where the relative equilibria are spectrally stable, and we give a complete classification of the spectral stability of these solutions, in the sense that, except on an algebraic curve in the space of parameters, we can determine if the corresponding relative equilibrium is spectrally stable or unstable. On 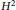${{H}^{2}}$, in the elliptic case, we prove that generically all Eulerian-relative equilibria are unstable; in the particular degenerate case when the two equal masses are negligible, we get that the corresponding solutions are spectrally stable. For the hyperbolic case we consider the system where the mass in the middle is negligible; in this case the Eulerian-relative equilibria are unstable.

Keywords

70F0770G60curved spacerelative equilibriumspectral stability
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 2 , 01 April 2018 , pp. 426 - 450
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Bolyai, J. and Bolyai, W., Geometrische Untersuchungen. Hrsg. P. Stäckel, Teubner, Leipzig-Berlin, 1913.Google Scholar
[2] Broucke, R., Stability of periodic orbits in the elliptic, restricted three-body problem, AIAA Journal , 7(1969), no. 6, 1003–1009.Google Scholar
[3] Diacu, F., On the singularities of the curved n-body problem. Trans. Amer. Math. Soc. 363(2011), no. 4, 2249–2264.http://dx.doi.org/10.1090/S0002-9947-2010-05251-1 Google Scholar
[4] Diacu, F., Relative equilibria of the curved N-body problem. Atlantis Press, Paris, 2012.http://dx.doi.org/10.2991/978-94-91216-68-8 Google Scholar
[5] Diacu, F., Martínez, R., Pérez-Chavela, E., and Simó, C., On the stability of tetrahedral relative equilibria in the positively curved 4-body problem. Phys. D 256/257(2013), 21–35.http://dx.doi.Org/10.1016/j.physd.2O13.04.007 Google Scholar
[6] Diacu, F. and Pérez-Chavela, E., Homographie solutions of the curved 3-body problem. J. Differential Equations 250(2011), 340–366.http://dx.doi.Org/10.101 6/j.jde.2O10.08.011 Google Scholar
[7] Diacu, F., Pérez-Chavela, E., and Santoprete, M., The n-body problem in spaces of constant curvature. Parti: Relative equilibria. J. Nonlinear Sci. 22(2012), 247–266.http://dx.doi.Org/10.1007/s00332-011-9116-z Google Scholar
[8] Diacu, F., Pérez-Chavela, E., and Santoprete, M., The n-body problem in spaces of constant curvature. Part IT. Singularities. J. Nonlinear Sci. 22(2012), 267–275.http://dx.doi.org/10.1007/s00332-011-9117-y Google Scholar
[9] García-Naranjo, L. C., Marrero, J. C., Pérez-Chavela, E., and Rodriguez-Olmos, M., Classification and stability of relative equilibria for the two-body problem in the hyperbolic space of dimension 2. J. Differential Equations 260(2016), no. 7, 6375–6404.http://dx.doi.Org/10.1016/j.jde.2015.12.044 Google Scholar
[10] Hernández-Garduño, A. and Stoica, C., Tagrangian relative equilibria in a modified three-body problem with a rotationally symmetric ellipsoid. SIAM J. Appl. Dyn. Syst. 14(2015), no. 1, 221–252.http://dx.doi.Org/10.1137/130949233 Google Scholar
[11] Killing, W., Die Mechanik in den nichteuklidischen Raumformen. J. Reine Angew. Math. 98(1885), 1–48.http://dx.doi.Org/10.1515/crll.1885.98.1 Google Scholar
[12] Martínez, R. and Simó, C., On the stability of the Tagrangian homographie solutions in a curved three-body problem on S2. Discrete Cont. Dyn. Syst. 33(2013), 1157–1175.Google Scholar
[13] Carifiena, J. F., Rañada, M. F., and Santander, M., Central potentials on spaces of constant curvature: the Kepler problem on the two-dimensional sphere S2 and the hyperbolic plane H2. J. Math. Phys. 46(2005), 052702, 25.http://dx.doi.Org/10.1063/1.1893214 Google Scholar
[14] Lipschitz, R., Extension of the planet-problem to a space of n dimensions and constant integral curvature. Quart. J. Pure Appl. Math. 12(1873), 349–370.Google Scholar
[15] Lovachevski, N. I., The new foundations of geometry with full theory of parallels. (Russian) In: Collected Works, V. 2, GITTL , Moscow, 159,1949, pp. 1835–1838.Google Scholar
[16] Mardling, R. A., Resonance, chaos and stability in the general three-body problem. Dynamical Evolution of Dense Stellar Systems Proceedings IAU Symposium , 246, 2007.Google Scholar
[17] Pérez-Chavela, E. and Sánchez Cerritos, J. M., Stability of Euler-Type relative equilibria in the curved three body problem. In: Hamiltonian systems and celestial mechanics, Trends in Mathematics , 4, Springer, Switzerland, 2015, pp. 59–63.http://dx.doi.Org/10.1007/978-3-319-22129-8J1 Google Scholar
[18] E. Pérez-Chavela, and Reyes-Victoria, J. G., An intrinsic approach in the curved n-body problem. The positive curvature case. Trans. Amer. Math. Soc. 364(2012), no. 7. 3805–3827.http://dx.doi.org/10.1090/S0002-9947-2012-05563-2 Google Scholar
[19] Schepetilov, A. B., Nonintegrability of the two-body problem in constant curvature spaces. J. Phys. A. Gen. 39(2006), 5787–5806.http://dx.doi.org/10.1088/0305-4470/39/20/011 Google Scholar
[20] Schering, E., Die Schwerkraft im Gaussischen Raume. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universitä zu Göttingen 1870(1870), 311–321.Google Scholar
[21] Zhu, S., Eulerian Relative Equilibria of the curved three 3-body problem in S2. Proc.s Amer. Math. Soc. 142(2014), 2837–2848.http://dx.doi.org/10.1090/S0002-9939-2014-11995-2 Google Scholar