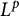1 Introduction
The theory of maximal monotone operators
${\boldsymbol {A}}:\mathcal {X}\rightrightarrows \mathcal {X}^{*}$
in Hilbert and reflexive Banach spaces provides a very powerful framework to solve nonlinear equations (see, e.g., the review [Reference Borwein11]). We recall that an operator
${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
(which we identify with its graph) is said to be monotone if
$$\begin{align*}\langle v-w, x-y\rangle\ge0\quad\text{for any }(x,v),\,(y,w)\in{\boldsymbol{A}},\end{align*}$$
while
${\boldsymbol {A}}$
is said to be maximal monotone if every proper extension of
${\boldsymbol {A}}$
fails to be monotone.
In the Hilbertian case, the theory can also be applied to differential inclusions of the form
$$ \begin{align} \frac{\mathrm{d}}{{\mathrm{d}} t} x(t)\in -{\boldsymbol{A}} x(t),\quad x(0)=x_{0} \end{align} $$
driven by a maximal monotone operator
${\boldsymbol {A}}$
and to prove the generation of a semigroup of contractions (see, e.g., [Reference Barbu6, Reference Brézis13]).
The notion of maximality of the (multivalued) operator
${\boldsymbol {A}}$
plays a crucial role, since by the Minty–Browder theorem it is equivalent to the solvability of the resolvent equation
$$ \begin{align} J(x)+\tau{\boldsymbol{A}} x\ni y, \end{align} $$
where J is the duality map from
$\mathcal {X}$
to
$\mathcal {X}^{*}$
[Reference Barbu6, Theorem 2.2]. In the Hilbertian framework, the solution to (1.2) corresponds to the solvability of the Implicit Euler Scheme associated with (1.1) and provides a general condition for the existence of a solution to (1.1). In this respect, an essential tool is the well-known fact that every monotone operator
${\boldsymbol {A}}$
admits a maximal extension [Reference Brézis13, Reference Debrunner and Flor18], whose domain is contained in the closed convex hull of the domain of
${\boldsymbol {A}}.$
Motivated by the study of operators in Bochner-
$L^{p}$
spaces
$\mathcal {X}=L^{p}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
(here
$(\Omega , {\mathcal {B}})$
is a standard Borel space endowed with a nonatomic probability measure
$\mathbb {P}$
and
$\mathsf {X}$
is a reflexive and separable Banach space) which are invariant by measure-preserving transformations of
$\Omega $
, in this paper we address the general problem of finding maximal extensions of monotone operators which are invariant by a group
$\mathsf {G}$
of suitable transformations of
$\mathcal {X}\times \mathcal {X}^{*}$
. More precisely, let us consider a group
$\mathsf {G}$
of linear isomorphisms acting on
$\mathcal {X}\times \mathcal {X}^{*}$
whose elements
$\mathsf {U}=(U,U')$
preserve the duality pairing and the norms in
$\mathcal {X}\times \mathcal {X}^{*}$
, i.e., for every
$(U,U')\in \mathsf {G}$
and every
$z=(x,v)\in \mathcal {X}\times \mathcal {X}^{*}$
, we have
$$ \begin{align} \langle U'v,Ux\rangle= \langle v,x\rangle,\quad |Ux|=|x|,\quad |U'v|_{*}=|v|_{*}. \end{align} $$
Given a monotone operator
${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
which is
$\mathsf {G}$
-invariant, i.e.,
$$ \begin{align} (x,v)\in {\boldsymbol{A}},\quad (U,U')\in \mathsf{G}\quad\Rightarrow\quad (Ux,U'v)\in {\boldsymbol{A}}, \end{align} $$
we will prove (see Theorem 2.5) that there exists a maximal extension
${\boldsymbol {\hat A}}$
of
${\boldsymbol {A}}$
preserving the
$\mathsf {G}$
-invariance; we will also find
${\boldsymbol {\hat A}}$
so that its proper domain
$\mathrm {D}({\boldsymbol {\hat {A}}})$
does not exceed the closed convex hull of
$\mathrm {D}({\boldsymbol {A}}).$
Since it is not clear how to adapt to this context the classical proof based on the Debrunner–Flor and Zorn lemma (see, e.g., [Reference Brézis13, Theorem 2.1 and Corollary 2.1, Chapter II]), we will use the powerful explicit construction of [Reference Bauschke and Wang8]. This is based on kernel averages of convex functionals and on the characterization of monotone and maximal monotone operators via suitable convex Lagrangians on
$\mathcal {X}\times \mathcal {X}^{*}$
, a deep theory started with the seminal paper [Reference Fitzpatrick19] (where the so-called Fitzpatrick’s function is introduced for the first time) and further developed in a more recent series of relevant contributions (see, e.g., [Reference Burachik and Svaiter14, Reference Ghoussoub22, Reference Martinez-Legaz and Théra24–Reference Penot26, Reference Visintin35] and the references therein).
The advantage of this direct approach is that it provides an explicit formula for the extension of
${\boldsymbol {A}}$
which behaves quite well with respect to the action of the group
$\mathsf {G}$
. As an intermediate step, which can be relevant also in other applications independently of
$\mathsf {G}$
-invariance, we will also show (Theorem 2.3) how to modify the construction of [Reference Bauschke and Wang8] in order to confine the domain of the extension
${\boldsymbol {\hat {A}}}$
to the closed convex hull of
$\mathrm {D}({\boldsymbol {A}})$
(see also [Reference Bauschke and Wang9, Theorem 2.13] for a partial result in this direction).
As a byproduct, we can adapt the same strategy of [Reference Bauschke and Wang9] to prove a version of the Kirszbraun–Valentine extension theorem (see [Reference Kirszbraun23, Reference Valentine33, Reference Valentine34]) for
$\mathsf {G}$
-invariant Lipschitz maps in Hilbert spaces (Theorem 2.11): it states that every L-Lipschitz map
$f:D\to \mathcal {H}$
defined in a subset D of an Hilbert space
$\mathcal {H}$
, whose graph is invariant with respect to the action of a group
$\mathsf {G}$
of isometries of
$\mathcal {H}$
, can be extended to an L-Lipschitz function
$\hat f:\mathcal {H}\to \mathcal {H}$
which is
$\mathsf {G}$
-invariant as well. The basic idea here still goes back to Minty: the graphs of nonexpansive maps in Hilbert spaces are in one-to-one correspondence with graphs of monotone maps via the Cayley transformation
$T:\mathcal {H}\times \mathcal {H}\to \mathcal {H}\times \mathcal {H}$
defined as
$$ \begin{align} T(y,w):=\frac 1{\sqrt 2}(y-w,y+w). \end{align} $$
It is worth noticing that such a correspondence allowed the authors of [Reference Reich and Simons28] to use for the first time the Fitzpatrick’s function to prove the Kirszbraun–Valentine theorem (see [Reference Kirszbraun23, Reference Valentine33, Reference Valentine34]), which states that every
$1$
-Lipschitz continuous map can be extended to the whole
$\mathcal {H}$
(see also [Reference Bauschke7] where this approach is improved in order to obtain an extension with an optimal range). The same correspondence, together with the explicit construction of a maximal extension of a monotone operator
${\boldsymbol {A}}$
in [Reference Bauschke and Wang8], is used in [Reference Bauschke and Wang9] to provide the first constructive proof of the Kirszbraun–Valentine theorem.
We will also provide in the Appendix an alternative proof based on another more recent explicit formula for such kind of extension given by [Reference Azagra, Le Gruyer and Mudarra5] (see also [Reference Azagra, Le Gruyer and Mudarra4]).
These results, besides being interesting by themselves, find interesting applications in the case when
$\mathcal {X}$
is the
$L^{p}$
-space of random variables
$$ \begin{align} \mathcal{X}=L^{p}(\Omega,{\mathcal{B}},\mathbb{P};\mathsf{X}),\!\!\quad \mathcal{X}^{*}=L^{{p}^{*}}(\Omega, {\mathcal{B}},\mathbb{P};\mathsf{X}^{*}),\!\!\quad p,p^{*}\in (1,+\infty), \ \frac 1p+\frac 1{p^{*}}=1, \end{align} $$
over a space of parametrizations
$(\Omega ,{\mathcal {B}},\mathbb {P})$
, where
$(\Omega ,{\mathcal {B}})$
is a standard Borel space,
$\mathbb {P}$
is a nonatomic probability measure, and
$\mathsf {X}$
is a separable and reflexive Banach space, while
$\mathsf {G}$
is a group of isomorphisms generated by measure-preserving maps, i.e.,
${\mathcal {B}}-{\mathcal {B}}$
measurable maps
$g:\Omega \to \Omega $
which are essentially injective and such that
$g_{\sharp}\mathbb {P}=\mathbb {P}$
, where
$g_{\sharp}\mathbb {P}$
denotes the push-forward of
$\mathbb {P}$
by g. Every measure-preserving isomorphism g induces an element
$\mathsf {U}_{g}$
of
$\mathsf {G}$
whose action on
$(X,X')\in \mathcal {X}\times \mathcal {X}^{*}$
is simply given by
$\mathsf {U}_{g}(X,X')= (X\circ g,X'\circ g)$
.
The interest for invariance by measure-preserving isomorphisms in
$\mathcal {X}\times \mathcal {X}^{*}$
is justified by its link with the stronger property of law invariance: a set
${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
is law invariant if whenever
$(X,X')\in {\boldsymbol {A}}$
, then
${\boldsymbol {A}}$
also contains all the pairs
$(Y,Y')\in \mathcal {X}\times \mathcal {X}^{*}$
with the same law of
$(X,X')$
, i.e.,
$(Y,Y')_{\sharp}\mathbb {P}=(X,X')_{\sharp}\mathbb {P}.$
It is clear that law invariant subsets of
$\mathcal {X}\times \mathcal {X}^{*}$
are also invariant by measure-preserving isomorphisms; using the results of [Reference Brenier and Gangbo12], we will show that the converse implication holds for closed sets: therefore, for closed sets, these two properties are in fact equivalent. Since the graph of a maximal monotone operator is closed, we obtain that a monotone operator in
$\mathcal {X}\times \mathcal {X}^{*}$
whose graph is invariant by the action of measure-preserving isomorphisms admits a maximal monotone extension which is law invariant (Theorem 4.4).
This framework is exploited in Section 3 (where we study the approximation of transport maps and plans by various classes of measure-preserving isomorphisms) and Section 4.
The Hilbertian setting when
$p=p^{*}=2$
and
$\mathsf {X}$
is an Hilbert space (so that
$\mathcal {X}=L^{2}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
is a Hilbert space as well that can be identified with its dual
$\mathcal {X}^{*}$
) provides an important case, which we will further exploit in [Reference Cavagnari, Savaré and Sodini17]. It turns out that maximal dissipative operators
$\boldsymbol {B}$
on
$L^{2}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
, invariant by measure-preserving isomorphisms, are the Hilbertian counterparts of maximal totally dissipative operators on the Wasserstein space
$\mathcal {P}_{2}(\mathsf {X})$
of laws, where
$\mathcal {P}_{2}(\mathsf {X})$
denotes the space of Borel probability measures with finite second moment endowed with the so-called Kantorovich–Rubinstein–Wasserstein distance
$W_{2}$
. The results obtained in Section 4 in the framework (1.6) are used in [Reference Cavagnari, Savaré and Sodini17] to develop a well-posedness theory for dissipative evolution equations in the metric space
$(\mathcal {P}_{2}(\mathsf {X}),W_{2})$
, together with a Lagrangian characterization for the solution of the corresponding Cauchy problem.
Besides the direct application of the general invariance extension result provided in Section 2, in Section 4, we also analyze further properties of Lipschitz functions and maximal dissipative operators on
$\mathcal {X}= L^{2}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
, which are invariant by measure-preserving isomorphisms. In particular, we prove that the effect of a Lipschitz invariant map
${\boldsymbol {L}}:\mathcal {X}\to \mathcal {X}$
on an element
$X\in \mathcal {X}$
can always be represented as
$$\begin{align*}{\boldsymbol{L}} X(w)=l(X(w),X_{\sharp}\mathbb{P}) \quad \text{for a.e}.~\omega\in \Omega\,,\end{align*}$$
where
$l:\mathcal {S}(\mathsf {X})\to \mathsf {X}$
is a (uniquely determined) continuous map defined in
$$\begin{align*}\mathcal{S}(\mathsf{X}):=\Big\{(x,\mu)\in \mathsf{X}\times {\mathcal{P}}_{2}(\mathsf{X})\,:\,x\in \operatorname{\mathrm{supp}}(\mu)\Big\}\end{align*}$$
whose sections
$l(\cdot ,\mu )$
are Lipschitz as well, for every
$\mu \in \mathcal {P}_{2}(\mathsf {X}).$
An important application of these results concerns the resolvent operator, the Moreau–Yosida approximation, and the semigroup associated with a maximal dissipative invariant operator
$\boldsymbol {B}$
in
$L^{2}(\Omega ,{\mathcal {B}},\mathbb {P}; \mathsf {X})$
, for which we obtain new relevant representation formulae (Theorem 4.12).
The above structural characterizations rely on various approximation properties for couplings between probability measures in terms of maps and measure-preserving transformations. We collect them in Section 3, with the aim to present many important results available in the literature (cf. [Reference Brenier and Gangbo12, Reference Carmona and Delarue16, Reference Gangbo and Tudorascu21, Reference Pratelli27]) in a unified framework and (in some cases) a slightly more general setting adapted to Section 4.
2 Extension of monotone operators and Lipschitz maps invariant by a group of isometries
Let
$\mathcal {X}$
be a reflexive Banach space with norm
$|\cdot |$
, and let
$\mathcal {X}^{*}$
be its dual endowed with the dual norm
$|\cdot |_{*}$
.
We denote by
$\mathsf {c}:\mathcal {X}^{*}\times \mathcal {X}\to \mathbb {R}$
, the duality pairing
$\langle \cdot , \cdot \rangle $
between
$\mathcal {X}^{*}$
and
$\mathcal {X}$
and by
$\mathcal {Z}$
the product space
$\mathcal {X}\times \mathcal {X}^{*}$
with dual
$\mathcal {Z}^{*}:=\mathcal {X}^{*}\times \mathcal {X}$
.
A (multivalued) operator
${\boldsymbol {A}}:\mathcal {X}\rightrightarrows \mathcal {X}^{*}$
(which we identify with its graph, a subset of
$ \mathcal {X} \times \mathcal {X}^{*}$
) is monotone if it satisfies
$$ \begin{align} \langle v-w, x-y \rangle \ge 0 \quad \text{ for every } (x,v), (y,w) \in {\boldsymbol{A}}. \end{align} $$
The proper domain
$\mathrm {D}({\boldsymbol {A}})\subset \mathcal {X}$
of
${\boldsymbol {A}}$
is just the projection on the first component of (the graph of)
${\boldsymbol {A}}.$
A monotone operator
${\boldsymbol {A}}$
is maximal if any monotone operator in
$\mathcal {X}\times \mathcal {X}^{*}$
containing
${\boldsymbol {A}}$
coincides with
${\boldsymbol {A}}.$
In order to address the extension problem of monotone operators
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
invariant by the action of a group of isometric isomorphisms, it is crucial to have some explicit formula providing a maximal extension of
${\boldsymbol {A}}$
. In this respect, the characterization of monotone and maximal monotone operators by means of suitable “contact sets” of convex functionals in
$\mathcal {X}\times \mathcal {X}^{*},$
started with the seminal paper [Reference Fitzpatrick19] and further developed in a more recent series of relevant contributions (see, e.g., [Reference Burachik and Svaiter14, Reference Ghoussoub22, Reference Martinez-Legaz and Théra24–Reference Penot26, Reference Visintin35] and the references therein), and the kernel averaging operation developed by [Reference Bauschke and Wang8] provide extremely powerful tools, that we are going to quickly recall in the next section. We will also show how to slightly improve this construction in order to obtain an explicit formula providing a maximal extension of
${\boldsymbol {A}}$
whose domain is contained in the closed convex hull of
$\mathrm {D}({\boldsymbol {A}})$
. In this connection, we mention that the existence of a maximal extension of
${\boldsymbol {A}}$
with the desired abovementioned optimality for the domain can be deduced by [Reference Bauschke7], thanks to the correspondence revealed by Minty between monotone operators and firmly nonexpansive mappings. Indeed, [Reference Bauschke7] uses the Fitzpatrick function to prove the Kirszbraun–Valentine extension theorem for firmly nonexpansive mappings with optimal range localization. However, part of the proof still relies on Zorn’s lemma and it is not entirely constructive.
2.1 Maximal extensions of monotone operators by self-dual Lagrangians
Following the presentation of [Reference Bauschke and Wang8, Reference Penot26], given a set
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
and its indicator function
$\mathrm {I}_{\boldsymbol {A}}$
, we consider the proper function
$\mathsf {c}_{{\boldsymbol {A}}}: \mathcal {X}^{*} \times \mathcal {X} \to (-\infty , +\infty ]$
defined as
$$\begin{align*}\mathsf{c}_{{\boldsymbol{A}}}(v,x):= \mathsf{c}(v,x)+\mathrm{I}_{\boldsymbol{A}}(x,v)= \begin{cases} \langle v, x \rangle, \quad &\text{ if } (x,v) \in {\boldsymbol{A}}, \\ + \infty, \quad &\text{ else}.\end{cases}\end{align*}$$
Notice that
$\mathsf {c}_{{\boldsymbol {A}}}$
has an affine minorant if
${\boldsymbol {A}}$
is monotone, in the sense that
$$\begin{align*}\mathsf{c}_{{\boldsymbol{A}}} (v,x) \ge \langle v_{0},x \rangle + \langle v,x_{0}\rangle - \langle v_{0}, x_{0} \rangle \quad \text{ for every } (v,x) \in \mathcal{X}^{*} \times \mathcal{X},\end{align*}$$
where
$(x_{0},v_{0})\in {\boldsymbol {A}}$
is an arbitrary given point.
Recalling that the convex conjugate
$g^{*}:\mathcal {Z}^{*} \to (-\infty ,+\infty ]$
of a proper function
$g: \mathcal {Z} \to (-\infty , +\infty ]$
with an affine minorant is defined as
$$ \begin{align*} g^{*}(v,x) &:= \sup_{(x_{0},v_{0}) \in {\mathcal{Z}}} \left \{ \langle v_{0},x \rangle + \langle v,x_{0}\rangle -g(x_{0},v_{0})\right \}, \quad (v,x) \in \mathcal{X}^{*} \times{\mathcal{X}}, \end{align*} $$
with an analogous definition in the case of a function
$h:\mathcal {Z}^{*} \to (-\infty ,+\infty ]$
, we can introduce the Fitzpatrick function
$\mathsf {f}_{\boldsymbol {A}}:\mathcal {Z}\to (-\infty ,+\infty ]$
and the convex l.s.c. relaxation
$\mathsf {p}_{\boldsymbol {A}}:\mathcal {Z}^{*}\to (-\infty ,+\infty ]$
of
$\mathsf {c}_{{\boldsymbol {A}}}$
:
$$ \begin{align} \mathsf{f}_{\boldsymbol{A}}:=\mathsf{c}_{{\boldsymbol{A}}}^{*}, \quad \mathsf{p}_{{\boldsymbol{A}}}:=\mathsf{f}_{\boldsymbol{A}}^{*}= \mathsf{c}_{{\boldsymbol{A}}}^{**}. \end{align} $$
It will be often useful to switch the order of the components of elements in
$\mathcal {X}\times \mathcal {X}^{*}$
: we will denote by
${\mathfrak {s}}:{\mathcal {X}}\times {\mathcal {X}}^{*} \to \mathcal {X}^{*}\times \mathcal {X}$
the switch map
$$ \begin{align} \mathfrak{s}(x,v):=(v,x). \end{align} $$
If g is any function defined in
$\mathcal {X} \times \mathcal {X}^{*}$
(resp. in
$\mathcal {X}^{*}\times \mathcal {X}$
), we set
$g^{\top }:=g\circ \mathfrak {s}$
(resp.
$g^{\top }:=g\circ \mathfrak {s}^{-1}$
). In particular,
$\mathsf {c}^{\top }$
is the duality pairing between
$\mathcal {X}$
and
$\mathcal {X}^{*}$
.
We collect in the following statement some useful properties.
Theorem 2.1 (Representation of monotone operators)
-
(1) If
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying
$f\ge \mathsf {c}^{\top }$
, then (2.4)and
$$ \begin{align} \text{the contact set } {\boldsymbol{A}}_f:=\Big\{(x,v)\in \mathcal{Z}: f(x,v)=\langle v,x\rangle \Big\} \text{ is monotone, } f^{*}\ge \mathsf{f}_{{\boldsymbol{A}}_{f}}^{\top}, \end{align} $$
(2.5)where
$$ \begin{align} {\boldsymbol{A}}_f\subset \boldsymbol{T}_f:=\Big\{(x,v)\in \mathcal{Z}: (v,x)\in \partial f(x,v)\Big\}, \end{align} $$
$\partial f$
denotes the subdifferential of f. An analogous statement holds for
$g:\mathcal {Z}^{*}\to (-\infty ,+\infty ]$
satisfying
$g\ge \mathsf {c}$
, by setting
${\boldsymbol {A}}_g:={\boldsymbol {A}}_{g^{\top }}.$
-
(2) If
${\boldsymbol {A}}$
is monotone, then (2.6)
$$ \begin{align} \mathsf{f}_{\boldsymbol{A}}^{\top}\le \mathsf{p}_{\boldsymbol{A}}\le \mathsf{c}_{\boldsymbol{A}}; \end{align} $$
(2.7)i.e.,
$$ \begin{align} \mathsf{p}_{\boldsymbol{A}}\ge \mathsf{c};\quad \mathsf{p}_{\boldsymbol{A}}=\mathsf{c}\quad \text{on }{\boldsymbol{A}}, \end{align} $$
${\boldsymbol {A}}\subset {\boldsymbol {A}}_{\mathsf {p}_{\boldsymbol {A}}}.$
-
(3) If
${\boldsymbol {A}}$
is a monotone operator and
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying
$\mathsf {c}^{\top }\le f\le \mathsf {p}_{\boldsymbol {A}}^{\top }$
, then the contact set
${\boldsymbol {A}}_f$
is a monotone extension of
${\boldsymbol {A}}.$
-
(4) If
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
is maximal monotone, then
$\mathsf {f}_{\boldsymbol {A}}\ge \mathsf {c}^{\top }$
. Conversely, if
${\boldsymbol {A}}$
is monotone and
$\mathsf {f}_{\boldsymbol {A}}\ge \mathsf {c}^{\top }$
, then (2.8)provides a maximal monotone extension of
$$ \begin{align} {\boldsymbol{\hat{A}}}:= \Big\{z\in \mathcal{Z}:\mathsf{f}_{\boldsymbol{A}}(z)= \mathsf{c}^{\top} (z)\Big\} = \Big\{z\in \mathcal{Z}: \mathsf{p}_{\boldsymbol{A}}(z)= \mathsf{c} (z)\Big\} \end{align} $$
${\boldsymbol {A}}$
.
-
(5) If
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying
$f\ge \mathsf {c}^{\top }$
, then
${\boldsymbol {A}}_f$
is maximal monotone if and only if
$f^{*}\ge \mathsf {c}$
and in this case
${\boldsymbol {A}}_f= {\boldsymbol {A}}_{(f^{*})^{\top }}.$
-
(6) If
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying the self-duality property (2.9)then
$$ \begin{align} f^{*}=f^{\top}, \end{align} $$
$f\ge \mathsf {c}^{\top }$
and the contact set
${\boldsymbol {A}}_f$
is maximal monotone.
Proof We give a few references and sketches for the proof.
(1) The inclusion in (2.5) follows by [Reference Fitzpatrick19, Theorem 2.4] and shows in particular that
${\boldsymbol {A}}_f$
is monotone since
$\mathbf {T}_f$
is monotone by [Reference Fitzpatrick19, Proposition 2.2]. Clearly,
$f^{\top } \le \mathsf {c}_{{\boldsymbol {A}}_f}$
so that, passing to the conjugates, the reverse inequality follows.
(2) The result in (2.6) is [Reference Penot26, Proposition 4(c)], while (2.7) is [Reference Penot26, Proposition 4(f)].
(3) This follows by (1) and (2).
(4) The first implication follows by [Reference Penot26, Theorem 5]. The second implication follows by [Reference Penot26, Theorem 6] choosing
$g:=f_{\boldsymbol {A}}$
and [Reference Burachik and Svaiter14, Theorem 3.1].
(5) The first part of the sentence is [Reference Penot26, Theorem 6], while the equality
${\boldsymbol {A}}_f={\boldsymbol {A}}_{(f^{*})^{\top }}$
can be found, e.g., in [Reference Burachik and Svaiter14, Theorem 3.1].
(6) This is contained in the statement and in the proof of [Reference Bauschke and Wang8, Fact 5.6].
The previous result suggests a strategy (cf. Theorem 2.2 below) to construct a maximal extension of a given monotone operator
${\boldsymbol {A}}$
starting from a convex and l.s.c. function
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
satisfying
$$ \begin{align} \mathsf{f}_{\boldsymbol{A}}\le f\le \mathsf{p}_{\boldsymbol{A}}^{\top}\quad\text{in }\mathcal{Z}. \end{align} $$
Using the kernel average introduced in [Reference Bauschke and Wang8], one obtains a self-dual Lagrangian
$R_f$
which satisfies
$\mathsf {f}_{\boldsymbol {A}}\le R_f\le \mathsf {p}_{\boldsymbol {A}}^{\top }$
, so that the contact set of
$R_f$
is a maximal monotone extension of
${\boldsymbol {A}}.$
We introduce a function
$$ \begin{align} \psi:\mathcal{Z}\to[0,+\infty)\ \text{satisfying the symmetry and self-duality condition} \quad \psi=\psi^{\vee}=(\psi^{*})^{\top}, \end{align} $$
where
$\psi ^\vee (z):=\psi (-z)$
for every
$z \in \mathcal {Z}.$
The assumption in (2.11), in particular, implies that
$$ \begin{align} \psi\text{ is continuous, convex, and } \psi(0)=\psi^{*}(0)=0, \end{align} $$
since
$$\begin{align*}0\le \psi(0)=\psi^{\top}(0)= \psi^{*}(0)=-\inf \psi\le 0. \end{align*}$$
A typical example is given by
$$ \begin{align} \psi(x,v):=\frac 1p|x|^{p}+\frac{1}{p^{*}}|v|_{*}^{p^{*}} \quad\text{where}\ p,p^{*}\in (1,+\infty)\ \text{are given conjugate exponents.} \end{align} $$
The following result is an immediate consequence of [Reference Bauschke and Wang8, Fact 5.6, Theorem 5.7, and Remark 5.8].
Theorem 2.2 (Kernel averages and maximal monotone extensions [Reference Bauschke and Wang8])
Let
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
be a monotone operator, and let
$\mathsf {f}_{\boldsymbol {A}}:=\mathsf {c}_{{\boldsymbol {A}}}^{*}, \mathsf {p}_{\boldsymbol {A}}:=\mathsf {c}_{{\boldsymbol {A}}}^{**}$
be defined as above and
$\psi :\mathcal {Z}\to [0,+\infty )$
a self-dual function as in (2.11). Let
$f: \mathcal {Z} \to (-\infty ,+\infty ]$
be a lower semicontinuous and convex function satisfying (2.10).
-
(1) The function
$R_f: \mathcal {Z} \to (-\infty ,+\infty ]$
defined as (2.14)is self-dual and satisfies the bound (2.10), i.e.,
$$ \begin{align} R_f(x,v):= \min_{(x,v)=\frac{1}{2}(x_1+x_{2},v_1+v_{2})} \left \{ \frac{1}{2}f(x_1,v_1) + \frac{1}{2}f^{*}(v_{2},x_{2})+\frac{1}{4} \psi(x_1-x_{2},v_1-v_{2}) \right \} \end{align} $$
$\mathsf {f}_{\boldsymbol {A}}\le R_f\le \mathsf {p}_{\boldsymbol {A}}^{\top }.$
-
(2) The operator
$\tilde {{\boldsymbol {A}}}$
defined as the contact set of
$R_f$
(2.15)is a maximal monotone extension of
$$ \begin{align} \tilde{{\boldsymbol{A}}} := \left \{ (x,v) \in \mathcal{Z} : R_f(x,v)=\langle v,x\rangle\right \} \end{align} $$
${\boldsymbol {A}}$
.
We want to show that, for a suitable choice of f as in the previous theorem, we can produce a maximal monotone extension of
${\boldsymbol {A}}$
with domain included in
$ D:=\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right )$
. We claim that such f can be defined as
$$ \begin{align} f(x,v):= \mathsf{f}_{\boldsymbol{A}}(x,v)+ \mathrm{I}_C(x,v), \quad (x,v) \in \mathcal{X} \times \mathcal{X}^{*},\quad C:=D\times \mathcal{X}^{*}, \end{align} $$
where
$\mathrm {I}_C$
is the indicator function of
$C=D\times \mathcal {X}^{*}$
, i.e.,
$\mathrm {I}_C(x,v)=0$
if
$x \in D$
and
$\mathrm {I}_C(x,v)=+\infty $
if
$x \notin D$
.
Theorem 2.3 (A maximal monotone extension with minimal domain)
Let
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
be a monotone operator, and let
$f:\mathcal {Z}\to (-\infty , + \infty ]$
be as in (2.16). The following hold:
-
(1) f is a l.s.c. and convex function such that
$\mathsf {f}_{\boldsymbol {A}} \le f \le \mathsf {p}_{\boldsymbol {A}}^{\top } $
. -
(2)
$\mathrm {D}(f)\subset C=D\times \mathcal {X}^{*}$
and
$ \mathrm {D}(f^{*}) \subset \mathfrak {s}(C)=\mathcal {X}^{*}\times D$
. -
(3) Defining
$R_f$
as in (2.14) and its contact set
$\tilde {\boldsymbol {A}}$
as in (2.15),
$\mathrm {D}(R_f)\subset C=D\times \mathcal {X}^{*}$
and
$\tilde {\boldsymbol {A}}$
provides a maximal extension of
${\boldsymbol {A}}$
with domain
$\mathrm {D}(\tilde {\boldsymbol {A}})\subset D.$
Proof (1) It is clear that f is convex and lower semicontinuous and
$f \ge \mathsf {f}_{\boldsymbol {A}}$
. On the other hand,
$f^{\top }\le \mathsf {c}_{\boldsymbol {A}}$
by (2.6) and since
$\mathrm {I}_C=0$
on
${\boldsymbol {A}}$
. It follows that
$f^{\top }\le \mathsf {c}_{\boldsymbol {A}}^{**}=\mathsf {p}_{\boldsymbol {A}}.$
(2) It is clear from the definition of f that
$f(x,v)=+\infty $
if
$x \notin D$
. Let us compute the conjugate
$f^{*}$
of f: by the Fenchel–Rockafellar duality theorem (see, e.g., [Reference Rockafellar29, Theorem 16.4]), we have that
$$\begin{align*}f^{*}=(\mathsf{f}_{\boldsymbol{A}}+\mathrm{I}_C)^{*} = \operatorname{\mathrm{cl}}(\mathsf{f}_{\boldsymbol{A}}^{*}\mathbin\Box \mathrm{I}^{*}_C)= \operatorname{\mathrm{cl}}(\mathsf{p}_{\boldsymbol{A}}\mathbin\Box \mathrm{I}^{*}_C ),\end{align*}$$
where
$\operatorname {\mathrm {cl}}$
denotes the lower semicontinuous envelope of a given function (i.e.,
$\operatorname {\mathrm {cl}}(h)$
is the largest lower semicontinuous function staying below h) and
$\mathbin \Box $
denotes the inf-convolution (or epigraphical sum) of two functions: if
$k,j:\mathcal {Z}^{*} \to (-\infty , + \infty ]$
, then
$k\mathbin \Box j$
is defined as
$$\begin{align*}(k\mathbin\Box j)(z):=\inf_{z_1,z_{2}\in \mathcal{Z}^{*}, z_1+z_{2}=z} k(z_1)+j(z_{2}), \quad z\in \mathcal{Z}^{*}.\end{align*}$$
Since
$\mathrm {I}_C(x,v)=\mathrm {I}_D(x)$
, we can easily compute its dual for every
$z=(v,x)\in \mathcal {X}^{*} \times \mathcal {X}$
$$ \begin{align*} \mathrm{I}_C^{*}(v,x)&= \sup_{(x_{0},v_{0}) \in \mathcal{X}^{*} \times \mathcal{X}} \langle v,x_{0} \rangle + \langle v_{0},x\rangle -\mathrm{I}_D(x_{0}) = \sup_{x_{0}\in D, v_{0} \in \mathcal{X}^{*}} \langle v_{0},x \rangle + \langle v,x_{0}\rangle\\ &= \mathrm{I}_{0}(x)+\sigma_D(v), \end{align*} $$
where
$\mathrm {I}_{0}$
is the indicator function of the singleton
$\{0\}$
and
$\sigma _D$
is the support function of D defined by
$$\begin{align*}\sigma_D(v):= \sup_{x_{0} \in D} \langle v,x_{0} \rangle, \quad v \in \mathcal{X}^{*}.\end{align*}$$
We thus have
$$ \begin{align*} (\mathsf{p}_{\boldsymbol{A}} \mathbin\Box \mathrm{I}^{*}_C)(v,x) &= \inf_{x_1+x_{2}=x,v_1+v_{2}=v} \mathsf{p}_{\boldsymbol{A}}(v_1,x_1)+\mathrm{I}_{0}(x_{2}) +\sigma_D(v_{2}) \\ &= \inf_{v_1+v_{2}=v} \mathsf{p}_{\boldsymbol{A}}(v_1,x)+\sigma_D(v_{2}). \end{align*} $$
Since
$\mathsf {p}_{\boldsymbol {A}} =\mathsf {c}_{\boldsymbol {A}}^{**}$
and
$\mathsf {c}_{{\boldsymbol {A}}}(v,x)=+\infty $
, if
$x\not \in D$
, we deduce that
$\mathsf {p}_{\boldsymbol {A}}(v,x)=+\infty $
if
$x\not \in D$
,
$\mathrm {D}(\mathsf {p}_{\boldsymbol {A}} \mathbin \Box \mathrm {I}^{*}_C)\subset \mathfrak {s}(C)= \mathcal {X}^{*}\times D$
, and therefore that
$\mathrm {D}(f^{*})\subset \operatorname {\mathrm {cl}}( \mathcal {X}^{*}\times D)=\mathcal {X}^{*} \times D$
.
(3) By the first claim and Theorem 2.2 with f as in (2.16), we obtain that
$\tilde {{\boldsymbol {A}}}$
is a maximal monotone extension of
${\boldsymbol {A}}$
. We only need to check that
$\mathrm {D}(\tilde {{\boldsymbol {A}}}) \subset D=\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right )$
. Since it is clear from the definition of contact set that
$\mathrm {D}(\tilde {\boldsymbol {A}})\subset \pi ^{\mathcal {X}}(\mathrm {D}(R_f))$
, it is sufficient to check that
$\mathrm {D}(R_f)\subset C$
.
Let
$(x,v) \in \mathrm {D}(R_f)$
, then by (2.14) we can find
$x_1,x_{2} \in \mathcal {X}$
and
$v_1,v_{2} \in \mathcal {X}^{*}$
such that
$(x,v)=\frac {1}{2}(x_1+x_{2},v_1+v_{2})$
and
$(x_1,v_1)\in \mathrm {D}(f)$
,
$(v_{2},x_{2})\in \mathrm {D} (f^{*})$
: in particular,
$x_1,x_{2}$
belong to the convex set D by (2) and therefore
$x\in D$
as well.
2.2 Extension of monotone operators invariant w.r.t. the action of a group of linear isomorphisms of
$\mathcal {X}\times \mathcal {X}^{*}$
We will now focus on operators which are invariant with respect to a group
$\mathsf {G}$
of bounded linear isomorphisms of
$\mathcal {Z}$
of the form
$\mathsf {U}=(U,U'):\mathcal {Z} \to \mathcal {Z}$
. For every
$z=(x,v)\in \mathcal {Z}$
, we thus have
$$ \begin{align} \mathsf{U}(z)=(Ux,U'v) \end{align} $$
and we assume that all the maps
$\mathsf {U}\in \mathsf {G}$
satisfy the following properties:
$$ \begin{align} \mathsf{c}^{\top}( \mathsf{U} z)=\mathsf{c}^{\top}(z),\quad \psi(\mathsf{U}z)=\psi(z) \quad\text{for every }z\in \mathcal{Z} \end{align} $$
for a fixed self-dual function
$\psi :\mathcal {Z}\to [0,+\infty )$
as in (2.11). Notice that the first identity in (2.18) implies
$$ \begin{align} \langle U'v,Ux\rangle= \langle v,x\rangle\quad\text{for every } (x,v)\in \mathcal{Z} \end{align} $$
so that
$U^{*}\circ U'$
(resp.
$(U')^{*}\circ U$
) is the identity in
$\mathcal {X}^{*}$
(resp. in
$\mathcal {X}$
), i.e.,
$U'=(U^{*})^{-1}=(U^{-1})^{*}$
is the transpose inverse of U.
Given
$\mathsf {U}=(U,U') \in \mathsf {G}$
, we define as usual
$\mathsf {U}^{\top }:=\mathfrak {s} \circ \mathsf {U}\circ \mathfrak {s}^{-1}=(U',U):\mathcal {Z}^{*}\to \mathcal {Z}^{*}$
observing that
$\mathsf {U}^{\top }$
coincides with the inverse transpose of
$\mathsf {U}$
with respect to the duality paring between
$z^{*}=(v^{*},x^{*})\in \mathcal {Z}^{*}$
and
$z=(x,v)\in \mathcal {Z}$
given by
$$ \begin{align*} \langle z^{*},z\rangle&= \langle v^{*},x\rangle+ \langle v,x^{*}\rangle= \mathsf{c}(v^{*},x)+\mathsf{c}^{\top}(x^{*},v), \end{align*} $$
since
$$ \begin{align*} \langle \mathsf{U}^{\top} z^{*},\mathsf{U}z\rangle &= \langle (U'v^{*},Ux^{*}), (Ux,U'v)\rangle= \langle U'v^{*},Ux\rangle +\langle U'v,Ux^{*}\rangle = \langle v^{*},x\rangle +\langle v,x^{*}\rangle \\&= \langle z^{*},z\rangle. \end{align*} $$
In particular, we have the formula
$$ \begin{align} \langle \mathsf{U}^{\top} z^{*},z \rangle=\langle z^{*},\mathsf{U}^{-1}z\rangle \quad\text{for every } z\in \mathcal{Z},\ z^{*}\in \mathcal{Z}^{*},\ \mathsf{U}\in \mathsf{G}. \end{align} $$
Definition 2.1 [
$\mathsf {G}$
-invariance] We say that a set
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
is
$\mathsf {G}$
-invariant if
$\mathsf {U} {\boldsymbol {A}}\subset {\boldsymbol {A}}$
for every
$\mathsf {U}\in \mathsf {G}$
(i.e.,
$(Ux,U'v)\in {\boldsymbol {A}}$
for every
$(x,v) \in {\boldsymbol {A}}$
and
$(U,U')\in \mathsf {G}$
). A function g defined in
$ \mathcal {X} \times \mathcal {X}^{*}$
(resp. in
$\mathcal {X}^{*}\times \mathcal {X}$
) is said to be
$\mathsf {G}$
-invariant if
$g \circ \mathsf {U}=g$
(resp.
$g\circ \mathsf {U}^{\top }=g$
) for every
$\mathsf {U}\in \mathsf {G}$
. A function
$h: \mathcal {X} \to \mathcal {X}^{*}$
is
$\mathsf {G}$
-invariant if its graph is
$\mathsf {G}$
-invariant as a subset of
$\mathcal {X} \times \mathcal {X}^{*}$
.
The following simple result clarifies the relation between
$\mathsf {G}$
-invariance of monotone operators and
$\mathsf {G}$
-invariance of the corresponding Lagrangian functions.
Proposition 2.4
-
(1) If
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is
$\mathsf {G}$
-invariant, then
$f^{*}$
is
$\mathsf {G}$
-invariant. -
(2) If
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
is a
$\mathsf {G}$
-invariant monotone operator, then the functions
$\mathsf {c}_{\boldsymbol {A}}, \mathsf {f}_{\boldsymbol {A}}, \mathsf {p}_{\boldsymbol {A}}$
defined in Section 2.1 are
$\mathsf {G}$
-invariant. -
(3) If
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a
$\mathsf {G}$
-invariant, l.s.c., and convex function satisfying
$f\ge \mathsf {c}^{\top }$
, then the contact set
${\boldsymbol {A}}_f$
defined as in (2.4) is
$\mathsf {G}$
-invariant. -
(4) If
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is
$\mathsf {G}$
-invariant, then the kernel average
$R_f$
defined as in (2.14) is
$\mathsf {G}$
-invariant as well.
Proof (1) We simply have, for every
$\mathsf {U}\in \mathsf {G}$
,
$$ \begin{align*} f^{*}(\mathsf{U}^{\top} z^{*}) &= \sup_{z\in \mathcal{Z}}\left\{ \langle \mathsf{U}^{\top} z^{*},z\rangle -f(z)\right\}= \sup_{z\in \mathcal{Z}}\left\{ \langle z^{*},\mathsf{U}^{-1} z\rangle -f(z)\right\} \\& = \sup_{z\in \mathcal{Z}}\left\{ \langle z^{*},\mathsf{U}^{-1} z\rangle -f(\mathsf{U}^{-1} z)\right\}= \sup_{\tilde z\in \mathcal{Z}}\left\{ \langle z^{*},\tilde z\rangle -f(\tilde z)\right\} =f^{*}(z^{*}), \end{align*} $$
where we applied (2.20), the fact that
$\mathsf {U}^{-1}\in \mathsf {G}$
, the
$\mathsf {G}$
-invariance of f, and the fact that
$\{\tilde z=\mathsf {U}^{-1}z:z\in \mathcal {Z}\}=\mathcal {Z}.$
(2) One immediately sees that
$\mathsf {c}_{\boldsymbol {A}}$
is
$\mathsf {G}$
invariant thanks to the
$\mathsf {G}$
-invariance of
${\boldsymbol {A}}$
and (2.18). The invariance of
$\mathsf {f}_{\boldsymbol {A}}$
and of
$\mathsf {p}_{\boldsymbol {A}}$
then follows by the previous claim.
(3) If
$z=(x,v)\in {\boldsymbol {A}}_f$
, we know that
$f(z)=\mathsf {c}^{\top }(z)$
. Since f is
$\mathsf {G}$
-invariant, (2.18) yields, for every
$\mathsf {U}\in \mathsf {G}$
,
$$ \begin{align*} f(\mathsf{U}z)= f(z)=\mathsf{c}^{\top}(z)= \mathsf{c}^{\top}(\mathsf{U}z) \end{align*} $$
so that
$\mathsf {U}z\in {\boldsymbol {A}}_f.$
(4) We first observe that the function
$$ \begin{align*} P(z_1,z_{2}):= \frac 12 f(z_1)+ \frac 12 f^{*}(\mathfrak{s}(z_{2}))+ \frac 14 \psi(z_1-z_{2}) \end{align*} $$
satisfies
$$ \begin{align} P(\mathsf{U}z_1,\mathsf{U}z_{2})= P(z_1,z_{2}), \end{align} $$
thanks to the invariance of f, the invariance of
$f^{*}$
from claim (1), and the invariance property of
$\psi $
stated in (2.18).
Since
$\mathsf {U}$
is a linear isomorphism, we also have
$$ \begin{align*} z=\frac 12 z_1+\frac 12 z_{2} \quad\Leftrightarrow\quad \mathsf{U}z=\frac 12 \mathsf{U}z_1+\frac 12 \mathsf{U}z_{2}. \end{align*} $$
Combining the above identities, we immediately get
$R_f(\mathsf {U}z)= R_f(z).$
We can now obtain our main result.
Theorem 2.5 (
$\mathsf {G}$
-invariant maximal monotone extensions)
Let
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
be a
$\mathsf {G}$
-invariant monotone operator with
$D:=\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right ).$
Then the function f given by (2.16) is
$\mathsf {G}$
-invariant and, defining
$R_f$
as in (2.14) and its contact set
$\tilde {{\boldsymbol {A}}}$
as in (2.15), then
$\tilde {\boldsymbol {A}}$
is a
$\mathsf {G}$
-invariant maximal monotone extension of
${\boldsymbol {A}}$
with domain included in
$\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right )$
.
Proof Let us first observe that
$C':=\mathrm {D}({\boldsymbol {A}})\times \mathcal {X}^{*}$
is
$\mathsf {G}$
-invariant, thanks to the invariance of
${\boldsymbol {A}}.$
Since every element of
$\mathsf {G}$
is linear, also
$\operatorname {co}(C')$
is
$\mathsf {G}$
-invariant. Eventually, since every element of
$\mathsf {G}$
is continuous,
$C:=\operatorname {\mathrm {cl}}(\operatorname {co}(C'))$
is
$\mathsf {G}$
-invariant as well.
By claim (2) of Proposition 2.4, we deduce that the function f given by (2.16) is
$\mathsf {G}$
-invariant. The invariance of
$\tilde {\boldsymbol {A}}$
then follows by applying Claims (4) and (3) of Proposition 2.4, recalling that
$R_f\ge \mathsf {c}^{\top }$
by Theorem 2.1(6). We conclude by Theorem 2.3.
2.3 Extension of invariant dissipative operators in Hilbert spaces
We now quickly apply the results of the previous Section 2.2 to the particular case of dissipative operators in Hilbert spaces. We adopt the dissipative viewpoint in view of applications to differential equations, but clearly all our statements apply to monotone operators as well. The main reference is [Reference Brézis13].
We consider a Hilbert space
$\mathcal {H}$
with norm
$|\cdot |$
, scalar product
$\langle \cdot , \cdot \rangle $
, and dual
$\mathcal {H}^{*}$
which we identify with
$\mathcal {H}$
. A multivalued operator
$\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
is dissipative if the operator
$$ \begin{align} {\boldsymbol{A}}=-\boldsymbol{B}:=\Big\{(x,-v):(x,v)\in \boldsymbol{B}\Big\} \end{align} $$
is monotone. More generally,
$\boldsymbol {B}$
is said to be
$\lambda $
-dissipative (
$\lambda \in \mathbb {R}$
) if
$$ \begin{align} \langle v-w,x-y\rangle\le\lambda |x-y|^{2}\quad \text{for every }(x,v),\ (y,w)\in \boldsymbol{B}. \end{align} $$
Remark 2.6 (
$\lambda $
-transformation)
Denoting by
$\boldsymbol {i}(\cdot )$
the identity function on
$\mathcal {H}$
, it is easy to check that
$\boldsymbol {B}$
is
$\lambda $
-dissipative if and only if
$\boldsymbol {B}^{\lambda }:= \boldsymbol {B}-\lambda \boldsymbol {i}$
is dissipative, or, equivalently,
$-\boldsymbol {B}^\lambda =\lambda \boldsymbol {i}-\boldsymbol {B}$
is monotone. Notice that
$\mathrm {D}(\boldsymbol {B})=\mathrm {D}(\boldsymbol {B}^\lambda )=\mathrm {D}(-\boldsymbol {B}^\lambda )$
.
We say that a
$\lambda $
-dissipative operator
$\boldsymbol {B}$
is maximal if
$\boldsymbol {B}$
is maximal w.r.t. inclusion in the class of
$\lambda $
-dissipative operators or, equivalently, if
$-\boldsymbol {B}^\lambda $
is a maximal monotone operator.
If
$\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
is a
$\lambda $
-dissipative operator, a maximal
$\lambda $
-dissipative extension of
$\boldsymbol {B}$
is any set
$\boldsymbol {C} \subset \mathcal {H} \times \mathcal {H}$
such that
$\boldsymbol {B} \subset \boldsymbol {C}$
and
$\boldsymbol {C}$
is maximal
$\lambda $
-dissipative.
As an immediate application of Theorem 2.5, we obtain an important result for dissipative operators which are invariant with respect to the action of a group
$\mathsf {G}$
of isometries.
Theorem 2.7 (Extension of invariant
$\lambda $
-dissipative operators)
Let
$\mathsf {G}_{\mathcal {H}}$
be a group of linear isometries of
$\mathcal {H}$
, and let
$\mathsf {G}:=\{(U,U):U\in \mathsf {G}_{\mathcal {H}}\}$
be the induced group of linear isometries in
$\mathcal {H}\times \mathcal {H}$
. Let
$\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
be a
$\lambda $
-dissipative operator which is
$\mathsf {G}$
-invariant (as a subset of
$\mathcal {H}\times \mathcal {H}$
). Then there exists a maximal
$\lambda $
-dissipative extension
$\hat {\boldsymbol {B}}$
of
$\boldsymbol {B}$
with
$\mathrm {D}(\hat {\boldsymbol {B}})\subset \overline {\operatorname {co}}\left (\mathrm {D}(\boldsymbol {B})\right )$
which is
$\mathsf {G}$
-invariant as well.
Proof We can choose the self-dual kernel
$$ \begin{align*} \psi(x,v):=\frac 12 |x|^{2}+\frac 12 |v|^{2}, \end{align*} $$
and we immediately get that
$\mathsf {G}$
satisfies (2.18). The statement is then an immediate application of Theorem 2.5 to the
$\mathsf {G}$
-invariant monotone operator
${\boldsymbol {A}}:=-\boldsymbol {B}^\lambda .$
Remark 2.8 If
$\boldsymbol {B}$
is a
$\mathsf {G}$
-invariant
$\lambda $
-dissipative operator which is maximal (with respect to inclusion) in the collection of
$\mathsf {G}$
-invariant
$\lambda $
-dissipative operators, then
$\boldsymbol {B}$
is maximal
$\lambda $
-dissipative.
We now derive a few more properties concerning the resolvent, the Yosida regularization and the minimal selection of a maximal
$\lambda $
-dissipative and
$\mathsf {G}$
-invariant operator
$\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
. For references on the corresponding definitions and properties, we refer to [Reference Brézis13], where the theory is developed in detail for the case
$\lambda =0$
. If
$\lambda \ne 0$
, analogous statements can be obtained and we refer the interested reader to [Reference Cavagnari, Savaré and Sodini17, Appendix A].
In the following, we use the notation
$\lambda ^+:= \lambda \vee 0$
and we set
$1/\lambda ^+=+\infty $
if
$\lambda ^+=0$
. We denote by
$\boldsymbol {B} x\equiv \boldsymbol {B}(x):=\{v\in \mathcal {H}:(x,v)\in \boldsymbol {B}\}$
the sections of
$\boldsymbol {B}$
, with
$x\in \mathcal {H}$
.
Recall that for every
$0<\tau <1/\lambda ^+$
, the resolvent
${\boldsymbol {J}_{\tau }}:=(\boldsymbol {i}-\tau \boldsymbol {B})^{-1}$
of
$\boldsymbol {B}$
is a
$(1-\lambda \tau )^{-1}$
-Lipschitz map defined on the whole
$\mathcal {H}$
. The minimal selection
$\boldsymbol {B}^\circ :\mathrm {D}(\boldsymbol {B})\to \mathcal {H}$
of
$\boldsymbol {B}$
is also characterized by
$$ \begin{align*}\boldsymbol{B}^\circ x=\displaystyle\lim_{\tau \downarrow 0}\frac{{\boldsymbol{J}_{\tau}} x-x}{\tau}. \end{align*} $$
The Yosida approximation of
$\boldsymbol {B}$
is defined by
$\boldsymbol {B}_{\tau }:=\frac {{\boldsymbol {J}_{\tau }}-\boldsymbol {i}}{\tau }$
. For every
$0<\tau <1/\lambda ^+$
,
$\boldsymbol {B}_{\tau }$
is maximal
$\frac {\lambda }{1-\lambda \tau }$
-dissipative and
$\frac {2-\lambda \tau }{\tau (1-\lambda \tau )}$
-Lipschitz continuous.
Moreover (cf. [Reference Brézis13, Proposition 2.6] or [Reference Cavagnari, Savaré and Sodini17, Appendix A]), the following hold:
$$ \begin{align} &\text{if}\ x \in \mathrm{D}(\boldsymbol{B}), \,\,(1-\lambda \tau)|\boldsymbol{B}_{\tau} x| \uparrow |{\boldsymbol{B}}^\circ x|, \text{as}\ \tau \downarrow 0, \end{align} $$
$$ \begin{align} &\text{if}\ x \notin \mathrm{D}(\boldsymbol{B}), \,\,|\boldsymbol{B}_{\tau} x| \to + \infty, \text{as}\ \tau \downarrow 0. \end{align} $$
Since
$\boldsymbol {B}$
is a maximal
$\lambda $
-dissipative operator, there exists a semigroup of
$e^{\lambda t}$
-Lipschitz transformations
$(\boldsymbol {S}_t)_{t \ge 0}$
with
$\boldsymbol {S}_t: \overline {\mathrm {D}(\boldsymbol {B})} \to \overline {\mathrm {D}(\boldsymbol {B})}$
s.t. for every
$x_{0}\in \mathrm {D}(\boldsymbol {B})$
the curve
$t \mapsto \boldsymbol {S}_t x_{0}$
is included in
$\mathrm {D}(\boldsymbol {B})$
and it is the unique locally Lipschitz continuous solution of the differential inclusion
$$ \begin{align} \begin{cases} \dot{x}_t \in \boldsymbol{B} x_t, \quad \text{ a.e. } t>0, \\ x {|_{t=0}} = x_{0}. \end{cases} \end{align} $$
We also have
$$ \begin{align} \lim_{h\downarrow0}\frac{\boldsymbol{S}_{t+h} x_{0}-\boldsymbol{S}_t x_{0}}h = \boldsymbol{B}^\circ(\boldsymbol{S}_tx_{0}),\quad \text{for every}\ x_{0}\in \mathrm{D}(\boldsymbol{B})\ \text{and every}\ t\ge 0 \end{align} $$
and
$$ \begin{align} \boldsymbol{S}_tx = \lim_{n \to + \infty} (\boldsymbol{J}_{t/n})^n x, \quad x \in \overline{\mathrm{D}(\boldsymbol{B})}, \, t \ge 0. \end{align} $$
Proposition 2.9 (Invariance of resolvents, Yosida regularizations, semigroups, and minimal selections)
Let
$\boldsymbol {B} \subset \mathcal {H} \times \mathcal {H}$
be a maximal
$\lambda $
-dissipative operator which is
$\mathsf {G}$
-invariant. Then, for every
$0<\tau <1/\lambda ^+,\,t\ge 0$
, the operators
${\boldsymbol {J}_{\tau }}$
,
$\boldsymbol {B}_{\tau }$
,
$\boldsymbol {S}_t$
,
$\boldsymbol {B}^\circ $
are
$\mathsf {G}$
-invariant.
Proof The identities
${\boldsymbol {J}_{\tau }} (Ux)=U({\boldsymbol {J}_{\tau }} x)$
and
$\boldsymbol {B}^\circ (Ux) = U(\boldsymbol {B}^\circ x)$
come from the
$\mathsf {G}$
-invariance of
$\boldsymbol {B}$
and the uniqueness property of the resolvent operator. The exponential formula (cf. (2.28))
$$ \begin{align*} \boldsymbol{S}_t x=\lim_{n\to\infty} ({\boldsymbol{J}_{t/n}})^n(x) \end{align*} $$
yields the
$\mathsf {G}$
-invariance of
$\boldsymbol {S}_t$
.
2.4 Extension of invariant Lipschitz maps in Hilbert spaces
We conclude this general discussion concerning
$\mathsf {G}$
-invariant sets and maps addressing the problem of the global extension of a
$\mathsf {G}$
-invariant Lipschitz map defined in a subset of a separable Hilbert space
$\mathcal {H}.$
As in Theorem 2.7, we consider a group
$\mathsf {G}_{\mathcal {H}}$
of isometric isomorphisms of
$\mathcal {H}$
inducing the group
$\mathsf {G}:=\{(U,U):U\in \mathsf {G}_{\mathcal {H}}\}$
in
$\mathcal {H}\times \mathcal {H}.$
In addition to Definition 2.1, we also give the following definition.
Definition 2.2 [
$\mathsf {G}_{\mathcal {H}}$
-invariance for
$\mathcal {H}$
-valued maps] We say that a function
$f:D\to \mathcal {H}$
, where
$D\subset \mathcal {H}$
, is
$\mathsf {G}_{\mathcal {H}}$
-invariant if its graph is
$\mathsf {G}$
-invariant:
$$ \begin{align} \text{for every}\ x\in D, \text{we have}\ Ux\in D\ \text{and}\ f(Ux)=Uf(x),\ \text{for every}\ U\in\mathsf{G}_{\mathcal{H}}. \end{align} $$
The Kirszbraun–Valentine theorem [Reference Kirszbraun23, Reference Valentine34] states that every Lipschitz function
$f:D\to \mathcal {H}$
defined in a subset D of
$\mathcal {H}$
with Lipschitz constant
$L\ge 0$
admits a Lipschitz extension
$F:\mathcal {H}\to \mathcal {H}$
whose Lipschitz constant coincides with L. We want to prove that it is possible to find such an extension preserving
$\mathsf {G}$
-invariance.
Our starting point is the following well-known fact, going back to Minty (see also [Reference Alberti and Ambrosio1]). We introduce the isometric Cayley transforms
$T, T^{-1}:\mathcal {H}\times \mathcal {H}\to \mathcal {H}\times \mathcal {H}$
$$ \begin{align} T(y,w):=\frac 1{\sqrt 2}(y-w,y+w),\quad T^{-1}(x,v):= \frac 1{\sqrt 2}(x+v,-x+v). \end{align} $$
Lemma 2.10 (Lipschitz and monotone graphs)
Let
$\boldsymbol {F},{\boldsymbol {A}}$
be two subsets of
$\mathcal {H}\times \mathcal {H}$
such that
${\boldsymbol {A}}=T(\boldsymbol {F})$
. The following two properties are equivalent:
-
(1)
$\boldsymbol {F}$
is the graph of a nonexpansive map f defined on the set D given by
$$\begin{align*}D:=\pi^1(\boldsymbol{F}) =\big\{y\in\mathcal{H}:(y,w)\in\boldsymbol{F} \text{ for some }w\in \mathcal{H}\big\};\end{align*}$$
-
(2)
${\boldsymbol {A}}$
is monotone.
Moreover, assuming that
${\boldsymbol {A}}$
is monotone, the following hold:
-
(i)
${\boldsymbol {A}}$
is maximal monotone if and only if
$D=\mathcal {H}.$
-
(ii)
${\boldsymbol {A}}$
is
$\mathsf {G}$
-invariant if and only if
$\boldsymbol {F}$
is
$\mathsf {G}$
-invariant (or, equivalently, f is
$\mathsf {G}_{\mathcal {H}}$
-invariant). -
(iii) If
${\boldsymbol {A}}'$
is a monotone extension of
${\boldsymbol {A}}$
and
$f':D'\to \mathcal {H}$
is the nonexpansive map associated with
$ \boldsymbol {F}':=T^{-1}({\boldsymbol {A}}')$
, then
$D':=\pi ^1(\boldsymbol {F}')\supset D$
and
$f'$
is an extension of
$f.$
Proof Let us take a pair of elements
$(x_i,v_i)=T(y_i,w_i)\in {\boldsymbol {A}}$
,
$i=1,2$
; we have
$y_i=\frac 1{\sqrt 2} (x_i+v_i)$
,
$w_i=\frac 1{\sqrt 2}(-x_i+v_i)$
so that
$$ \begin{align} 2|y_1-y_{2}|^{2}= |x_1+v_1-(x_{2}+v_{2})|^{2} &= |x_1-x_{2}|^{2} + |v_1-v_{2}|^{2} +2\langle x_1-x_{2},v_1-v_{2}\rangle, \end{align} $$
$$ \begin{align} 2|w_1-w_{2}|^{2} =|-x_1+v_1-(-x_{2}+v_{2})|^{2} &= |x_1-x_{2}|^{2} + |v_1-v_{2}|^{2} -2\langle x_1-x_{2},v_1-v_{2}\rangle, \end{align} $$
and then
$$ \begin{align} |w_1-w_{2}|^{2} \le |y_1-y_{2}|^{2} \quad \Leftrightarrow \quad \langle x_1-x_{2},v_1-v_{2}\rangle \ge 0. \end{align} $$
This proves the first statement.
Concerning (i), it is sufficient to recall that the domain D of f coincides with the image of
$h({\boldsymbol {A}})$
where
$h(x,v):=\frac 1{\sqrt 2}(x+v)$
and we know that
${\boldsymbol {A}}$
is maximal monotone if and only if such an image coincides with
$\mathcal {H}$
(cf. [Reference Brézis13, Proposition 2.2(ii)]).
The second property (ii) is an immediate consequence of the invertibility of T and of the linearity of the transformations of
$\mathsf {G}$
so that for every
$\mathsf {U}=(U,U)\in \mathsf {G}$
, we have
$T\circ \mathsf {U}= \mathsf {U}\circ T$
.
Let us eventually consider claim (iii): we clearly have
$\boldsymbol {F}'= T^{-1}({\boldsymbol {A}}')\supset T^{-1}({\boldsymbol {A}}) = \boldsymbol {F}$
and therefore
$D'=\pi ^1(\boldsymbol {F}')\supset \pi ^1(\boldsymbol {F})=D$
. On the other hand, since both
$\boldsymbol {F}'$
and
$\boldsymbol {F}$
are the graph of a nonexpansive map,
$\boldsymbol {F}'\cap (D\times \mathcal {H})= \boldsymbol {F}\cap (D\times \mathcal {H})$
and therefore the restriction of
$f'$
to D coincides with f.
We can now state our result concerning the extension of
$\mathsf {G}$
-invariant Lipschitz maps.
Theorem 2.11 (Extension of
$\mathsf {G}$
-invariant Lipschitz maps)
Let us suppose that
$f:D\to \mathcal {H}$
is L-Lipschitz and
$\mathsf {G}_{\mathcal {H}}$
-invariant according to (2.29). Then there exists a L-Lipschitz map
$\hat f:\mathcal {H}\to \mathcal {H}$
extending f which is
$\mathsf {G}_{\mathcal {H}}$
-invariant as well.
Proof Up to a rescaling, it is not restrictive to assume that
$L=1$
so that f is nonexpansive.
Let
$\boldsymbol {F}\subset \mathcal {H}\times \mathcal {H}$
be the graph of f, and let
${\boldsymbol {A}}:=T(\boldsymbol {F})$
. By Lemma 2.10, we know that
${\boldsymbol {A}}$
is a monotone
$\mathsf {G}$
-invariant operator
We can now apply Theorem 2.7 to find a maximal monotone extension
${\boldsymbol {\hat {A}}}$
of
${\boldsymbol {A}}$
which is still
$\mathsf {G}$
-invariant.
Setting
$\boldsymbol {\hat F}:= T^{-1}({\boldsymbol {\hat {A}}})$
, we can eventually apply Lemma 2.10 to obtain that
$\boldsymbol {\hat F}$
is the graph of a nonexpansive map
$\hat f:\hat D\to \mathcal {H}.$
Moreover, Claim (i) shows that
$\hat D=\mathcal {H}$
so that
$\hat f$
is globally defined, Claim (ii) shows that
$\hat f$
is
$\mathsf {G}_{\mathcal {H}}$
-invariant, and Claim (iii) ensures that
$\hat f$
is an extension of f.
3 Borel partitions and almost optimal couplings
In this section, we collect some useful results concerning Borel isomorphisms and partitions of standard Borel spaces. These results, besides being interesting by themselves, will also turn out to be useful in Section 4, where we will deal with a particular group of isometric isomorphisms on Banach spaces of
$L^{p}$
-type.
We start by fixing the fundamental definitions and notations involved in the statements of the main theorems of this section, which are presented in Section 3.2. These results concern the approximation of arbitrary couplings between probability measures by couplings which are concentrated on maps, through the action of measure-preserving transformations. In particular, Corollary 3.15 concerns the approximation of bistochastic measures by the graph of measure-preserving maps and it is written here in the general context of a standard Borel space
$(\Omega , {\mathcal {B}})$
endowed with a nonatomic probability measure
$\mathbb {P}$
. This result relies on the analogous property stated for the d-dimensional Lebesgue measure in [Reference Brenier and Gangbo12, Theorem 1.1]. In the same spirit of Corollary 3.15, Corollary 3.16 provides an approximation result for the law of a pair of measurable random variables defined on
$(\Omega , {\mathcal {B}},\mathbb {P})$
with values in a pair of separable Banach spaces. A consequence of this result is the key lemma [Reference Cardaliaguet15, Lemma 6.4] (cf. also [Reference Carmona and Delarue16, Lemma 5.23, p. 379]), which states that if X and Y are random variables with the same law, then X can be approximated by Y through the action of a sequence of measure-preserving transformations. Finally, we reported a fundamental result in Optimal Transportation Theory, concerning the equivalence between the Monge and the Kantorovich formulations (see [Reference Pratelli27, Theorem B]). This is the content of Proposition 3.18 where the result is written using the language of random variables (cf. also [Reference Gangbo and Tudorascu21, Lemma 3.13]), so as to be easily recalled in Section 4.
In order to introduce all the technical tools used to state and prove all these properties, in Section 3.1, we list some well-known facts about standard Borel spaces.
Definition 3.1 (Standard Borel spaces and nonatomic measures)
A standard Borel space
$(\Omega , {\mathcal {B}})$
is a measurable space that is isomorphic (as a measure space) to a Polish space. Equivalently, there exists a Polish topology
$\tau $
on
$\Omega $
such that the Borel sigma algebra generated by
$\tau $
coincides with
${\mathcal {B}}$
. We say that a positive finite measure
$\mathfrak {m}$
on
$(\Omega , {\mathcal {B}})$
is nonatomic (also called atomless or diffuse) if
$\mathfrak {m}(\{\omega \}) = 0$
for every
$\omega \in \Omega $
(notice that
$\{\omega \} \in {\mathcal {B}}$
since it is compact in any Polish topology on
$\Omega $
).
We notice that, being
$(\Omega ,{\mathcal {B}})$
standard Borel,
$\mathfrak {m}$
is nonatomic if and only if for every
$B\in {\mathcal {B}}$
with
$\mathfrak {m}(B)>0$
, there exists
$B'\in {\mathcal {B}},\ B'\subset B$
, such that
$0<\mathfrak {m}(B')<\mathfrak {m}(B).$
Definition 3.2 (Partitions)
If
$(\Omega , {\mathcal {B}})$
is a standard Borel space and
$N \in \mathbb {N}$
, a family of subsets
$\mathfrak {P}_N=\{\Omega _{N,k}\}_{k \in I_N} \subset {\mathcal {B}}$
, where
$I_N:=\{0, \dots , N-1\}$
, is called an N-partition of
$(\Omega , {\mathcal {B}})$
if
$$\begin{align*}\bigcup_{k\in I_N}\Omega_{N,k}=\Omega, \quad \Omega_{N,k}\cap \Omega_{N,h}=\emptyset \text{ if }h,k\in I_N,\, h\neq k.\end{align*}$$
If
$(\Omega , {\mathcal {B}})$
is a standard Borel space endowed with a nonatomic, positive finite measure
$\mathfrak {m}$
, we denote by
$\mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m})$
the class of
${\mathcal {B}}$
-
${\mathcal {B}}$
-measurable maps
$g:\Omega \to \Omega $
which are essentially injective and measure-preserving, meaning that there exists a full
$\mathfrak {m}$
-measure set
$\Omega _{0} \in {\mathcal {B}}$
such that g is injective on
$\Omega _{0}$
and
$g_\sharp \mathfrak {m}=\mathfrak {m}$
, where
$g_\sharp \mathfrak {m}$
is the push forward of
$\mathfrak {m}$
through g. We recall that, if X and Y are Polish spaces,
$f: X \to Y$
is a Borel map, and
$\mu $
is a nonnegative and finite measure on X, then
$f_\sharp \mu $
is defined by
$$ \begin{align} \int_{Y} \varphi \,\mathrm{d} (f_{\sharp}\mu) = \int_X \varphi \circ f \,\mathrm{d} \mu \end{align} $$
for every
$\varphi :Y\to \mathbb {R}$
bounded (or nonnegative) Borel function.
If
$\mathcal {A} \subset {\mathcal {B}}$
is a sigma algebra on
$\Omega $
, we denote by
$\mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m}; \mathcal {A})$
the subset of
$\mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m})$
of
$\mathcal {A}-\mathcal {A}$
measurable maps. Finally,
${\mathrm {Sym}(I_N)}$
denotes the set of permutations of
$I_N$
, i.e., bijective maps
$\sigma : I_N \to I_N$
.
We consider the partial order on
$\mathbb {N}$
given by
$$ \begin{align} m\prec n\quad\Leftrightarrow\quad m\mid n, \end{align} $$
where
$m\mid n$
means that
$n/m\in \mathbb {N}$
. We write 
if
$m \prec n$
and
$m \ne n$
.
Definition 3.3 (Segmentations)
Let
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
$\mathfrak {m}$
, and let
${\mathfrak {N}} \subset \mathbb {N}$
be an unbounded directed set w.r.t.
$\prec $
. We say that a collection of partitions
$(\mathfrak {P}_N)_{N \in {\mathfrak {N}}}$
of
$\Omega $
, with corresponding sigma algebras
${\mathcal {B}}_N:= \sigma (\mathfrak {P}_N)$
, is an
${\mathfrak {N}}$
-segmentation of
$(\Omega , {\mathcal {B}}, \mathfrak {m})$
if:
-
(1)
$\mathfrak {P}_N= \{\Omega _{N,k}\}_{k \in I_N}$
is an N-partition of
$(\Omega , {\mathcal {B}})$
for every
$N \in {\mathfrak {N}}$
, -
(2)
$\mathfrak {m}(\Omega _{N,k})=\mathfrak {m}(\Omega )/N$
for every
$k\in I_N$
and every
$N \in {\mathfrak {N}}$
, -
(3) if
$M\mid N=KM$
, then
$\bigcup _{k=0}^{K-1}\Omega _{N,mK+k}=\Omega _{M,m}$
,
$m\in I_{M}$
, -
(4)
$\sigma \left ( \left \{ {\mathcal {B}}_N \mid N \in {\mathfrak {N}} \right \} \right ) = {\mathcal {B}}$
.
In this case, we call
$(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
an
${\mathfrak {N}}$
-refined standard Borel measure space.
Remark 3.1 It is clear that
${\mathcal {B}}_M \subset {\mathcal {B}}_N$
if and only if
$M \mid N$
.
Example 3.2 The canonical example of
${\mathfrak {N}}$
-refined standard Borel measure space is
$$\begin{align*}([0,1), \mathcal{B}([0,1)), \lambda^c, (\mathfrak{I}_N)_{N \in {\mathfrak{N}}}),\end{align*}$$
where
$\lambda ^c$
is the one-dimensional Lebesgue measure restricted to
$[0,1)$
and weighted by a constant
$c>0$
and
$\mathfrak {I}_N=(I_{N,k})_{k \in I_N}$
with
$I_{N,k}:=[k/N,(k+1)/N)$
,
$k \in I_N$
and
$N \in {\mathfrak {N}}$
.
3.1 Technical tools on standard Borel spaces and measure-preserving isomorphisms
We start with the following fundamental result that follows by, e.g., [Reference Royden30, Theorem 9, Chapter 15].
Theorem 3.3 (Isomorphisms of standard Borel spaces)
Let
$(\Omega , {\mathcal {B}})$
and
$(\Omega ', {\mathcal {B}}',)$
be standard Borel spaces endowed with nonatomic, positive finite measures
$\mathfrak {m}$
and
$\mathfrak {m}'$
, respectively, such that
$\mathfrak {m}(\Omega ) = \mathfrak {m}'(\Omega ')$
. Then there exist two measurable functions
$\varphi : \Omega \to \Omega '$
and
$\psi : \Omega '\to \Omega $
such that
$$ \begin{align} \psi \circ \varphi = \boldsymbol{i}_{\Omega} \mathfrak{m}-\text{a.e.~in}\ \Omega, \quad \varphi \circ \psi = \boldsymbol{i}_{\Omega'} \mathfrak{m}'-\text{a.e.~in}\ \Omega', \quad \varphi_\sharp \mathfrak{m} = \mathfrak{m}', \quad \psi_\sharp \mathfrak{m}'=\mathfrak{m}. \end{align} $$
Corollary 3.4 Let
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
$\mathfrak {m}$
, and let
$(\Omega ', {\mathcal {B}}')$
be a standard Borel space. Then, for every nonatomic, positive measure
$\mu $
on
$(\Omega ', {\mathcal {B}}')$
such that
$\mu (\Omega ')= \mathfrak {m}(\Omega )$
, there exists a measurable map
$X: \Omega \to \Omega '$
such that
$X_\sharp \mathfrak {m} = \mu $
.
Lemma 3.5 (Existence of
${\mathfrak {N}}$
-segmentations)
For any standard Borel space
$(\Omega , {\mathcal {B}})$
endowed with a nonatomic, positive finite measure
$\mathfrak {m}$
and any unbounded directed set
${\mathfrak {N}} \subset \mathbb {N}$
w.r.t.
$\prec $
, there exists an
${\mathfrak {N}}$
-segmentation of
$(\Omega , {\mathcal {B}}, \mathfrak {m})$
.
Proof Let
$([0,1), \mathcal {B}([0,1)), \lambda ^c, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
be the
${\mathfrak {N}}$
-refined standard Borel space of Example 3.2 with
$c=\mathfrak {m}(\Omega )$
. Since
$([0,1), \mathcal {B}([0,1)))$
is a standard Borel space endowed with the nonatomic, positive finite measure
$\lambda ^c$
such that
$\mathfrak {m}(\Omega ) = \lambda ^c([0,1))$
, by Theorem 3.3, we can find measurable maps
$\varphi :[0,1) \to \Omega $
,
$\psi : \Omega \to [0,1)$
and two subsets
$\Omega _{0} \in {\mathcal {B}}$
,
$U \in \mathcal {B}([0,1))$
such that
$\mathfrak {m}(\Omega _{0})=\lambda ^c(U)=0$
,
$\varphi \circ \psi = \boldsymbol {i}_{\Omega \setminus \Omega _{0}}$
,
$\psi \circ \varphi = \boldsymbol {i}_{[0,1)\setminus U}$
,
$\varphi _\sharp \lambda ^c=\mathfrak {m}$
and
$\psi _\sharp \mathfrak {m}=\lambda ^c$
. We can thus define
$$\begin{align*}\Omega_{N,0} = \varphi(I_{N,0}\setminus U) \cup \Omega_{0}, \quad \Omega_{N,k} = \varphi(I_{N,k}\setminus U), \quad k \in I_N\setminus\{0\}, \, N \in {\mathfrak{N}}.\end{align*}$$
Setting
$\mathfrak {P}_N := \{\Omega _{N,k}\}_{k \in I_N}$
for every
$N \in {\mathfrak {N}}$
, it is easy to check that
$(\mathfrak {P}_N)_{N \in {\mathfrak {N}}}$
is a
${\mathfrak {N}}$
-segmentation of
$(\Omega , {\mathcal {B}}, \mathfrak {m})$
.
Definition 3.4 (Compatible partitions)
If
$(\Omega , {\mathcal {B}})$
and
$(\Omega ', {\mathcal {B}}')$
are standard Borel spaces endowed with nonatomic, positive finite measures
$\mathfrak {m}$
and
$\mathfrak {m}'$
, respectively, such that
$\mathfrak {m}(\Omega )=\mathfrak {m}'(\Omega ')$
and
$\mathfrak {P}_N =\{\Omega _{N,k}\}_{k \in I_N}$
and
$\mathfrak {P}^{\prime }_N =\{\Omega ^{\prime }_{N,k}\}_{k \in I_N}$
are N-partitions of
$(\Omega , {\mathcal {B}})$
and
$(\Omega ', {\mathcal {B}}')$
, respectively, we say that
$\mathfrak {P}_N$
and
$\mathfrak {P}^{\prime }_N$
are
$\mathfrak {m}-\mathfrak {m}'$
compatible if
$$\begin{align*}\mathfrak{m}(\Omega_{N,k}) = \mathfrak{m}'(\Omega^{\prime}_{N,k}) \quad \forall k \in I_N.\end{align*}$$
Lemma 3.6 (Isomorphisms preserving compatible partitions)
Let
$(\Omega , {\mathcal {B}})$
and
$(\Omega ', {\mathcal {B}}')$
be standard Borel spaces endowed with nonatomic, positive finite measures
$\mathfrak {m}$
and
$\mathfrak {m}'$
, respectively, such that
$\mathfrak {m}(\Omega )= \mathfrak {m}'(\Omega ')$
, and let
$\mathfrak {P}_N=\{\Omega _{N,k}\}_{k \in I_N}$
and
$\mathfrak {P}^{\prime }_N=\{\Omega ^{\prime }_{N,k}\}_{k \in I_N}$
be two
$\mathfrak {m}-\mathfrak {m}'$
compatible N-partitions of
$(\Omega , {\mathcal {B}})$
and
$(\Omega ', {\mathcal {B}}')$
, respectively, for some
$N \in \mathbb {N}$
. Then there exist two functions
$\varphi : \Omega \to \Omega '$
and
$\psi : \Omega '\to \Omega $
such that:
-
(1)
$\varphi $
is
${\mathcal {B}}$
-
${\mathcal {B}}'$
measurable and
$\sigma (\mathfrak {P}_N)$
-
$\sigma (\mathfrak {P}^{\prime }_N)$
measurable; -
(2)
$\psi $
is
${\mathcal {B}}'$
-
${\mathcal {B}}$
measurable and
$\sigma (\mathfrak {P}^{\prime }_N)$
-
$\sigma (\mathfrak {P}_N)$
measurable; -
(3) for every
$k \in I_N$
, it holds (3.4)
$$ \begin{align} \varphi(\Omega_{N,k}) \subset \Omega^{\prime}_{N, k}, \quad \psi(\Omega^{\prime}_{N,k}) \subset \Omega_{N, k}; \end{align} $$
-
(4) for every
$I \subset I_N$
, it holds where the subscript I denotes the restriction to
$$ \begin{align*} \psi_I \circ \varphi_I &= \boldsymbol{i}_{\Omega_I} \mathfrak{m}_I-\text{ a.e. in}\ \Omega_I,\\ \varphi_I \circ \psi_I &= \boldsymbol{i}_{\Omega^{\prime}_I} \mathfrak{m}_I'-\text{a.e. in}\ \Omega_I',\\ (\varphi_I)_\sharp \mathfrak{m}_I &= \mathfrak{m}_I',\\ (\psi_I)_\sharp \mathfrak{m}_I'&=\mathfrak{m}_I, \end{align*} $$
$\cup _{k \in I} \Omega _{N,k}$
or
$\cup _{k \in I} \Omega ^{\prime }_{N,k}$
.
Proof Applying Theorem 3.3 to the standard Borel spaces
$(\Omega _{\{k\}}, {\mathcal {B}}_{\{k\}})$
and
$(\Omega ^{\prime }_{\{k\}}, {\mathcal {B}}^{\prime }_{\{k\}})$
endowed, respectively, with the nonatomic, positive finite measures
$\mathfrak {m}_{\{k\}}$
and
$\mathfrak {m}^{\prime }_{\{k\}}$
for every
$k \in I_N$
, we obtain the existence of measurable functions
$\varphi _{k}, \psi _{k}$
satisfying (3.3) for each couple
$\Omega _{N,k}$
,
$\Omega ^{\prime }_{N,k}$
. It is then enough to define
$$\begin{align*}\varphi(\omega) := \varphi_{k}(\omega) \quad \text{ if } \omega \in \Omega_{N,k}, \quad \psi(\omega') := \psi_{k}(\omega') \quad \text{ if } \omega' \in \Omega^{\prime}_{N,k}.\end{align*}$$
Notice that (3.4) is satisfied by construction.
Corollary 3.7 (Lifting permutations to isomorphisms)
Let
$(\Omega , {\mathcal {B}}, \mathfrak {m})$
be a standard Borel space endowed with a nonatomic, positive finite measure
$\mathfrak {m}$
, and let
$\mathfrak {P}_N=\{\Omega _{N,k}\}_{k \in I_N}$
be an N-partition of
$(\Omega , {\mathcal {B}})$
for some
$N \in \mathbb {N}$
such that
$\mathfrak {m}(\Omega _{N,k})= \mathfrak {m}(\Omega )/N$
for every
$k \in I_N$
. If
$\sigma \in {\mathrm {Sym}(I_N)}$
, there exists a measure-preserving isomorphism
$g \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m}; \sigma (\mathfrak {P}_N))$
such that
$$\begin{align*}(g_{k})_{\sharp}\mathfrak{m}|_{\Omega_{N,k}} = \mathfrak{m}|_{\Omega_{N,\sigma(k)}} \quad \forall k \in I_N, \end{align*}$$
where
$g_{k}$
is the restriction of g to
$\Omega _{N,k}$
.
Proof It is enough to apply Lemma 3.6 to the standard Borel spaces
$(\Omega , {\mathcal {B}})$
and
$(\Omega ', {\mathcal {B}}')$
=
$(\Omega , {\mathcal {B}})$
endowed with the nonatomic, positive finite measures
$\mathfrak {m}$
and
$\mathfrak {m}'=\mathfrak {m}$
, respectively, with the N-partitions
$\mathfrak {P}_N$
and
$\mathfrak {P}^{\prime }_N=\{\Omega _{N,\sigma (k)}\}_{k \in I_N}$
, respectively.
Corollary 3.8 Let
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
$\mathfrak {m}$
, and let
$\Omega _{0}, \Omega _1 \in {\mathcal {B}}$
be such that
$\mathfrak {m}(\Omega _{0})=\mathfrak {m}(\Omega _1)>0$
and
$\Omega _{0} \cap \Omega _1 = \emptyset $
. Then there exists a measure-preserving isomorphism
$g \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m})$
such that
$$\begin{align*}(g_{0})_\sharp \mathfrak{m} |_{\Omega_{0}} = \mathfrak{m} |_{\Omega_{1}}, \quad (g_1)_\sharp \mathfrak{m} |_{\Omega_{1}} = \mathfrak{m} |_{\Omega_{0}}, \quad g(\omega)= \omega \text{ in } \Omega \setminus (\Omega_{0} \cup \Omega_1),\end{align*}$$
where
$g_i$
is the restriction of g to
$\Omega _{k}$
,
$k=0,1$
.
Proof Applying Corollary 3.7 to the standard Borel space
$(\Omega _{0} \cup \Omega _1,{\mathcal {B}}|_{\Omega _{0} \cup \Omega _1})$
endowed with the nonatomic, positive finite measure
$ \mathfrak {m}|_{\Omega _{0} \cup \Omega _1}$
with the
$2$
-Borel partition
$\mathfrak {P}_{2}= \{\Omega _{k}\}_{k=0,1}$
and
$\sigma $
sending
$0$
to
$1$
, we obtain the existence of a measure-preserving isomorphism
$\tilde {g} \in \mathrm {S}(\Omega _{0} \cup \Omega _1,{\mathcal {B}}|_{\Omega _{0} \cup \Omega _1}, \mathfrak {m}|_{\Omega _{0} \cup \Omega _1})$
such that
$$\begin{align*}(\tilde{g}_{0})_\sharp \mathfrak{m} |_{\Omega_{0}} = \mathfrak{m} |_{\Omega_{1}}, \quad (\tilde{g}_1)_\sharp \mathfrak{m} |_{\Omega_{1}} = \mathfrak{m} |_{\Omega_{0}}, \end{align*}$$
where
$\tilde {g}_i$
is the restriction of
$\tilde {g}$
to
$\Omega _{k}$
,
$k=0,1$
. It is then enough to define
$g: \Omega \to \Omega $
as
$$\begin{align*}g(\omega) = \begin{cases} \tilde{g}(\omega), \quad &\text{ if } \omega \in \Omega_{0} \cup \Omega_1, \\ \omega, \quad &\text{ if } \omega \in \Omega \setminus (\Omega_{0} \cup \Omega_1). \end{cases}\\[-34pt] \end{align*}$$
The next result is a particular case of Doob’s Martingale Convergence Theorem for Banach-valued maps (see [Reference Stroock32, Theorem 6.1.12]). We recall that a filtration on
$(\Omega , {\mathcal {B}})$
is a sequence
$(\mathcal {F}_n)_{n \in \mathbb {N}}$
of sub-sigma algebras of
${\mathcal {B}}$
such that
$\mathcal {F}_n \subset \mathcal {F}_{n+1}$
.
Theorem 3.9 Let
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
$\mathfrak {m}$
, let
$(\mathcal {F}_n)_{n \in \mathbb {N}}$
be a filtration on
$(\Omega , {\mathcal {B}})$
such that
$ \sigma \left ( \left \{ \mathcal {F}_n \mid n \in \mathbb {N} \right \} \right ) = {\mathcal {B}}$
, let
$\mathsf {X}$
be a separable Banach space, and let
$p\in [1,\infty ).$
Then, given
$X \in L^{p}(\Omega , {\mathcal {B}}, \mathfrak {m};\mathsf {X})$
, the
$\mathsf {X}$
-valued martingale
$$\begin{align*}X_n:= {\mathbb{E}}_{\mathfrak{m}} \left [ X \mid \mathcal{F}_n \right ], \quad n \in \mathbb{N}, \end{align*}$$
satisfies
$$ \begin{align} \lim_{n \to + \infty}X_n = X \end{align} $$
both
$\mathfrak {m}$
-a.e. and in
$L^{p}(\Omega , {\mathcal {B}}, \mathfrak {m};\mathsf {X})$
.
In general, the collection of sigma algebras
$(\mathcal {B}_N)_{N \in {\mathfrak {N}}}$
associated with a segmentation according to Definition 3.3 is not a filtration since it fails to be ordered by inclusion (recall Remark 3.1). However, it is always possible to extract from
$(\mathcal {B}_N)_{N \in {\mathfrak {N}}}$
a filtration still satisfying item (4) in Definition 3.3. More precisely, we have the following result.
Lemma 3.10 (Cofinal filtrations)
Let
${\mathfrak {N}} \subset \mathbb {N}$
be an unbounded directed subset w.r.t.
$\prec $
. Then there exists a totally ordered cofinal sequence
$(b_n)_n \subset {\mathfrak {N}}$
satisfying:
-
•
for every
$n \in \mathbb {N}$
, -
• for every
$N\in \mathbb {N}$
, there exists
$n\in \mathbb {N}$
such that
$N\mid b_n.$
for every 
In particular, for every
${\mathfrak {N}}$
-refined standard Borel measure space
$(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
, it holds that
$({\mathcal {B}}_{b_n})_{n \in \mathbb {N}}$
is a filtration on
$(\Omega , {\mathcal {B}})$
,
$$ \begin{align} \text{for every}\ N \in {\mathfrak{N}},\ \text{there exists}\ n \in \mathbb{N}\ \text{such that } {\mathcal{B}}_N \subset {\mathcal{B}}_{b_n}, \end{align} $$
and
$\sigma \left ( \left \{ {\mathcal {B}}_{b_n} \mid n \in \mathbb {N} \right \} \right ) = {\mathcal {B}}$
.
For every
$p \in [1,+\infty )$
and every separable Banach space
$\mathsf {X}$
, we thus have that
$$ \begin{align} \bigcup_{N \in {\mathfrak{N}}} L^{ p}(\Omega, {\mathcal{B}}_N, \mathfrak{m}; \mathsf{X}) \text{ is dense in } L^{ p}(\Omega, {\mathcal{B}}, \mathfrak{m}; \mathsf{X}). \end{align} $$
Proof Since
${\mathfrak {N}}$
is unbounded and directed, for every finite subset
$\mathfrak {M} \subset {\mathfrak {N}}$
, the quantity
is well defined. Let
$(a_n)_n \subset \mathbb {N}$
be an enumeration of
${\mathfrak {N}}$
and consider the following sequence defined by induction
$$\begin{align*}b_{0}=a_{0}, \quad b_{n+1}= \text{succ} \left (\{a_{n+1},b_n\} \right ), \quad n \in \mathbb{N}.\end{align*}$$
Then 
for every
$n \in \mathbb {N}$
and (3.6) holds for
$(b_n)_n$
and any
${\mathfrak {N}}$
-refined standard Borel measure space
$(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
.
In the next lemma, we show that, given two distinct points
$\omega , \omega "$
, they can always be separated by some partition
$\mathfrak {P}_N$
for
$N \in {\mathfrak {N}}$
sufficiently large.
Lemma 3.11 (Separation property)
Let
$(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be an
${\mathfrak {N}}$
-refined standard Borel measure space. Then there exists
$\Omega _{0} \in {\mathcal {B}}$
with
$\mathfrak {m}(\Omega _{0})=0$
such that for every
$\omega ', \omega " \in \Omega \setminus \Omega _{0}$
,
$\omega ' \ne \omega "$
, there exists
$M \in {\mathfrak {N}}$
such that for every
$N\in {\mathfrak {N}}$
,
$M\mid N$
, there exist
$k', k" \in I_{N}$
,
$k' \ne k"$
with
$\omega ' \in \Omega _{N, k'}$
and
$\omega " \in \Omega _{N,k"}$
.
Proof Let
$(b_n)_n\subset {\mathfrak {N}}$
be a totally ordered cofinal sequence as in Lemma 3.10, and let
$\tau $
be a Polish topology on
$\Omega $
such that
${\mathcal {B}}$
coincides with the Borel sigma algebra generated by
$\tau $
. By [Reference Bogachev10, Proposition 6.5.4], there exists a countable family
$\mathcal {F}$
of
$\tau $
-continuous functions
$f: \Omega \to [0,1]$
separating the points of
$\Omega $
, meaning that for every
$\omega ', \omega " \in \Omega $
,
$\omega ' \ne \omega "$
, there exists
$f \in \mathcal {F}$
such that
$f(\omega ') \ne f(\omega ")$
. Since
$\mathcal {F} \subset L^{2}(\Omega , {\mathcal {B}}, \mathfrak {m}; \mathbb {R})$
, by Theorem 3.9 with
$\mathcal {F}_n:={\mathcal {B}}_{b_n}$
, for every
$f \in \mathcal {F}$
, there exists an
$\mathfrak {m}$
-negligible set
$\Omega _f$
such that
$$\begin{align*}\lim_{n \to + \infty} {\mathbb{E}}_{\mathfrak{m}} \left [ f \mid\sigma \left ( \mathfrak{P}_{b_n} \right ) \right ](\omega) = f(\omega) \quad \forall \omega \in \Omega \setminus \Omega_f.\end{align*}$$
Let
$\Omega _{0} := \cup _{f \in \mathcal {F}} \Omega _f$
, and let
$\omega ', \omega " \in \Omega \setminus \Omega _{0}$
,
$\omega ' \ne \omega "$
. We can find
$f \in \mathcal {F}$
such that
$f(\omega ') \ne f(\omega ")$
. Thus, there exists
$M=b_m \in {\mathfrak {N}}$
such that
$$\begin{align*}{\mathbb{E}}_{\mathfrak{m}} \left [ f \mid\sigma \left ( \mathfrak{P}_{M} \right ) \right ](\omega') \ne {\mathbb{E}}_{\mathfrak{m}} \left [ f \mid\sigma \left ( \mathfrak{P}_{M} \right ) \right ](\omega").\end{align*}$$
Since
${\mathbb {E}}_{\mathfrak {m}} \left [ f \mid \sigma \left ( \mathfrak {P}_{M} \right ) \right ]$
is constant on every
$\Omega _{M,k}$
,
$k \in I_{M}$
, we conclude that the points
$\omega '$
and
$\omega "$
belong to different elements of
$\mathfrak {P}_{M}$
, and therefore they also belong to different elements of
$\mathfrak {P}_{N}$
for every
$N\in {\mathfrak {N}}$
multiple of M.
Proposition 3.12 (Segmentation preserving isomorphisms)
Let
$(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
and
$(\Omega ', {\mathcal {B}}', \mathfrak {m}', (\mathfrak {P}^{\prime }_N)_{N \in {\mathfrak {N}}})$
be
${\mathfrak {N}}$
-refined standard Borel measure spaces such that
$\mathfrak {m}(\Omega ) = \mathfrak {m}'(\Omega ')$
. Then there exist two measurable functions
$\varphi : \Omega \to \Omega '$
and
$\psi : \Omega '\to \Omega $
such that for every
$N \in {\mathfrak {N}}$
and every
$I \subset I_N$
, it holds
$$ \begin{align*} \psi_I \circ \varphi_I &= \boldsymbol{i}_{\Omega_I} \mathfrak{m}_I-\text{a.e. in}\ \Omega_I, \quad \varphi_I \circ \psi_I = \boldsymbol{i}_{\Omega^{\prime}_I}\ \mathfrak{m}_I'-\text{ a.e. in}\ \Omega_I',\\ (\varphi_I)_\sharp \mathfrak{m}_I &= \mathfrak{m}_I', \quad (\psi_I)_\sharp \mathfrak{m}_I'=\mathfrak{m}_I, \end{align*} $$
where the subscript I denotes the restriction to
$\cup _{k \in I} \Omega _{N,k}$
or
$\cup _{k \in I} \Omega ^{\prime }_{N,k}$
.
Proof By Lemma 3.10, it is enough to prove the statement in case
${\mathfrak {N}} = (b_n)_n$
, where
$(b_n)_n \subset \mathbb {N}$
is strictly
$\prec $
-increasing sequence and
$(\Omega ', {\mathcal {B}}', \mathfrak {m}', (\mathfrak {P}^{\prime }_N)_{N \in {\mathfrak {N}}})$
is
$([0,1), \mathcal {B}([0,1)), \lambda ^c, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
as in Example 3.2 with
$c= \mathfrak {m}(\Omega )$
. By Lemma 3.6, we can find for every
$n \in \mathbb {N}$
two measurable maps
$\varphi _n: \Omega \to [0,1)$
and
$\psi _n:[0,1) \to \Omega $
satisfying the thesis of Lemma 3.6 for the standard Borel spaces
$(\Omega , {\mathcal {B}})$
and
$([0,1), \mathcal {B}([0,1))$
endowed with nonatomic, positive, and finite measures
$\mathfrak {m}$
and
$\lambda ^c$
, respectively, and the
$\mathfrak {m}-\lambda ^c$
compatible
$b_n$
-partitions of
$(\Omega , {\mathcal {B}})$
and
$([0,1), \mathcal {B}([0,1)))$
given by
$\mathfrak {P}_{b_n}$
and
$\mathfrak {I}_{b_n}$
, where we recall from Example 3.2 that
$\mathfrak {I}_{b_n}= (I_{b_n,k})_{k \in I_{b_n}}$
with
$I_{b_n,k}=[k/b_n, (k+1)/b_n)$
. Since
$\sum _n b_n^{-1} < + \infty $
, for every
$\omega \in \Omega $
, the sequence
$(\varphi _n(\omega ))_n \subset [0,1)$
is Cauchy, hence converges. We thus have the existence of a measurable map
$\varphi : \Omega \to [0,1)$
such that
$$\begin{align*}\varphi(\omega) = \lim_n \varphi_n (\omega) \quad \forall \omega \in \Omega.\end{align*}$$
If
$n \in \mathbb {N}$
,
$k \in I_{b_n}$
, and
$ \xi \in \mathrm {C}_b(I_{b_n,k})$
, then
$$ \begin{align*} \int_{I_{b_n, k}} \xi \,\mathrm{d} \varphi_\sharp \mathfrak{m} &= \int_{\Omega_{b_n,k}} \xi(\varphi(\omega)) \,\mathrm{d} \mathfrak{m}(\omega) = \lim_m \int_{\Omega_{b_n,k}} \xi(\varphi_m(\omega)) \,\mathrm{d} \mathfrak{m}(\omega) \\ & = \lim_m \int_{I_{b_n,k}} \xi \,\mathrm{d} \lambda^c = \int_{I_{b_n,k}} \xi\,\mathrm{d} \lambda^c, \end{align*} $$
since for m sufficiently large
$(\varphi _m)_\sharp \mathfrak {m}|_{\Omega _{b_n,k}}=\lambda ^c|_{I_{b_n,k}}$
by Lemma 3.6. This shows that
$\varphi _\sharp \mathfrak {m} |_{\Omega _{b_n,k}} = \lambda ^c|_{I_{b_n,k}}$
for every
$k \in I_{b_n}$
and every
$n \in \mathbb {N}$
. To conclude, it is enough to show that
$\varphi $
is
$\mathfrak {m}$
-essentially injective. Let
$\Omega _{0} \subset \Omega $
be the
$\mathfrak {m}$
-negligible subset of
$\Omega $
given by Lemma 3.11, and let
$\Omega _1:= \varphi ^{-1}(J)$
, where
$$\begin{align*}J := \left \{ k/b_n \mid k \in I_{b_n}, \, n \in \mathbb{N} \right \} \subset [0,1).\end{align*}$$
Since
$\lambda ^c(J)=0$
, then
$\mathfrak {m}(\Omega _1)=0$
; let
$\omega ', \omega " \in \Omega \setminus (\Omega _{0} \cup \Omega _1)$
. Then there exists
$M \in \mathbb {N}$
such that
$\omega '$
and
$\omega "$
belong to different elements of
$\mathfrak {P}_{b_n}$
for every
$n \ge M$
. By (3.4) and Lemma 3.11, we can find
$k',k" \in I_{b_M}$
with
$k \ne k'$
such that
$\varphi _n(\omega ') \in I_{b_{M}, k'}$
and
$\varphi _n(\omega ") \in I_{b_{M}, k"}$
for every
$n \ge M$
. Thus,
$\varphi (\omega ') \in \overline {I_{b_{M}, k'}}$
and
$\varphi (\omega ') \in \overline {I_{b_{M}, k"}}$
; however, since
$$\begin{align*}\overline{I_{b_{M}, k'}} \cap \overline{I_{b_{M}, k"}} \subset J,\end{align*}$$
it must be that
$\varphi (\omega ') \ne \varphi (\omega ").$
3.2 Approximation of couplings by using measure-preserving isomorphisms
If X is a Polish space, we denote by
$\mathcal {P}(X)$
the space of Borel probability measures on X which is endowed with the weak (or narrow) topology: a sequence
$(\mu _n)_n \subset \mathcal {P}(X)$
converges to
$\mu \in \mathcal {P}(X)$
if
$$\begin{align*}\lim_n \int_X \varphi \,\mathrm{d} \mu_n = \int_X \varphi \,\mathrm{d} \mu \end{align*}$$
for every
$\varphi :X \to \mathbb {R}$
continuous and bounded. In this case, we write
$\mu _n \to \mu $
in
$\mathcal {P}(X)$
.
If
$X,Y$
are Polish spaces and
$(\mu ,\nu )\in \mathcal {P}(X)\times \mathcal {P}(Y)$
, we define the set of admissible transport plans
$$ \begin{align} \Gamma(\mu, \nu) := \left \{ \boldsymbol{\gamma} \in \mathcal{P}(X \times Y) \mid \pi^{1}_{\sharp} \boldsymbol{\gamma} = \mu \, , \, \pi^{2}_{\sharp} \boldsymbol{\gamma} = \nu \right \}, \end{align} $$
where
$\pi ^i$
,
$i=1,2$
, denotes the projection on the ith component and we call
$\pi ^{i}_{\sharp }\boldsymbol {\gamma }$
the ith marginal of
$\boldsymbol {\gamma }$
.
Definition 3.5 (Wasserstein spaces)
Let
$\mathsf {X}$
be a separable Banach space,
$\mu \in \mathcal {P}(\mathsf {X})$
, and
$p\ge 1$
. We define the space
$$ \begin{align} \mathcal{P}_p(\mathsf{X}) := \{ \mu \in \mathcal{P}(\mathsf{X}) \mid \int_{\mathsf{X}} |x|^{p} \,\mathrm{d} \mu(x) < + \infty \}. \end{align} $$
Given
$\mu ,\nu \in \mathcal {P}_p(\mathsf {X})$
, we define the
$L^{p}$
-Wasserstein distance
$W_p$
by
$$ \begin{align} W_p^{p}(\mu, \nu) &:= \inf \left \{ \int_{\mathsf{X} \times \mathsf{X}} |x-y|^{p} \,\mathrm{d} \boldsymbol{\gamma}(x,y) \mid \boldsymbol{\gamma} \in \Gamma(\mu, \nu) \right \}. \end{align} $$
We denote by
$\Gamma _o(\mu , \nu )$
the (nonempty, compact, and convex) subset of admissible plans in
$\Gamma (\mu , \nu )$
realizing the infimum in (3.10).
We recall that
$(\mathcal {P}_p(\mathsf {X}), W_p)$
is a complete and separable metric space. Moreover, if
$(\mu _n)_{n\in \mathbb {N}}\subset \mathcal {P}_p(\mathsf {X})$
and
$\mu \in \mathcal {P}_p(\mathsf {X})$
, the following holds (see [Reference Ambrosio, Gigli and Savaré3, Proposition 7.1.5 and Lemma 5.1.7]):
$$ \begin{align} \mu_n\to\mu\text{ in }\mathcal{P}_p(\mathsf{X}),\text{ as }n\to+\infty \quad\Longleftrightarrow\quad\begin{cases}\mu_n\to\mu \text{ in }\mathcal{P}(\mathsf{X}),\\ \int_{\mathsf{X}} |x|^{p} \,\mathrm{d} \mu_n\to\int_{\mathsf{X}} |x|^{p} \,\mathrm{d} \mu, \end{cases} \text{ as }n\to+\infty. \end{align} $$
We refer, e.g., to [Reference Ambrosio, Gigli and Savaré3, Chapter 7] for a more comprehensive introduction to Wasserstein distances.
The following result is an application of [Reference Brenier and Gangbo12, Theorem 1.1]. We will use the following notation: if
$\mathsf {X}_1$
and
$\mathsf {X}_{2}$
are sets and
$X_1:\mathsf {X}_1\to \mathsf {X}_1$
,
$X_{2}:\mathsf {X}_{2}\to \mathsf {X}_{2}$
, we denote by
$X_1\otimes X_{2}:\mathsf {X}_1\times \mathsf {X}_{2}\to \mathsf {X}_1\times \mathsf {X}_{2}$
the map
$(x_1,x_{2})\mapsto (X_1(x_1),X_{2}(x_{2}))$
.
Theorem 3.13 (Approximation of bistochastic couplings)
Let
$(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be a
${\mathfrak {N}}$
-refined standard Borel probability space. Then, for every
$\boldsymbol {\gamma } \in \Gamma (\mathbb {P}, \mathbb {P})$
, there exist a totally ordered strictly increasing sequence
$(N_n)_n \subset {\mathfrak {N}}$
and maps
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{N_n})$
such that, for every separable Banach spaces
$\mathsf {Z}, \mathsf {Z}'$
and every
$Z \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z})$
,
$Z' \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z}')$
, it holds
$$ \begin{align} (Z \otimes Z')_\sharp (\boldsymbol{i}_{\Omega}, g_n)_{\sharp} \mathbb{P}\to (Z\otimes Z')_\sharp \boldsymbol{\gamma} \text{ in } \mathcal{P}(\mathsf{Z}\times \mathsf{Z}'). \end{align} $$
Proof By Lemma 3.10, it is not restrictive to assume that
${\mathfrak {N}}=(b_n)_n$
for a totally ordered strictly increasing sequence
$(b_n)_n$
,
$n\in \mathbb {N}$
. We divide the proof in several steps.
(1) Let
$([0,1), \mathcal {B}([0,1)), \lambda ^1, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
be the
${\mathfrak {N}}$
-refined standard Borel probability space of Example 3.2 with
$c=1$
. Then, for every
$\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
, there exist a strictly increasing sequence
$(N_n)_n \subset \mathbb {N}$
and maps
$g_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
such that
$$\begin{align*}(\boldsymbol{i}_{[0,1)}, g_n)_\sharp \lambda^1 \to \boldsymbol{\gamma}\ \textit{in}\ \mathcal{P}([0,1) \times [0,1)).\end{align*}$$
Let
$\bar {\mathcal {L}}$
be the one-dimensional Lebesgue measure restricted to
$[0,1]$
, and let
$\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
. Let
$\boldsymbol {\mu } \in \mathcal {P}([0,1] \times [0,1]) $
be an extension of
$\boldsymbol {\gamma }$
to
$[0,1] \times [0,1]$
such that
$\boldsymbol {\mu } \in \Gamma (\bar {\mathcal {L}}, \bar {\mathcal {L}})$
. In [Reference Brenier and Gangbo12, Theorem 1.1], it is proven that it is possible to find a strictly increasing sequence
$(N_n)_n \subset \mathbb {N}$
and maps
$(f_n)_n \subset \mathrm {S}([0,1], \mathcal {B}([0,1]), \bar {\mathcal {L}})$
such that for every
$n \in \mathbb {N}$
, there exists
$\sigma _n \in {\mathrm {Sym}(I_{2^{N_n}})}$
such that
$$ \begin{align} f_n(x) = x - x_{N_n, k} + x_{N_n, \sigma_n(k)}, \quad x \in I_{2^{N_n}, k}, \quad k \in I_{2^{N_n}}, \end{align} $$
with
$x_{m,j}$
being the center of
$I_{2^m, j}$
, and satisfying
$$ \begin{align} (\boldsymbol{i}_{[0,1]}, f_n)_\sharp \bar{\mathcal{L}} \to \boldsymbol{\mu}\ {in}\ \mathcal{P}([0,1]\times [0,1]). \end{align} $$
If we call
$g_n$
the restriction of
$f_n$
to
$[0,1)$
,
$n \in \mathbb {N}$
, we get that
$g_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
for every
$n \in \mathbb {N}$
and
$$\begin{align*}(\boldsymbol{i}_{[0,1)}, g_n)_\sharp \lambda^1 \to \boldsymbol{\gamma} \ {in}\ \mathcal{P}([0,1)\times [0,1)). \end{align*}$$
This proves the first step only in case
$b_n=2^n$
. However, it can be easily checked that the proof of [Reference Brenier and Gangbo12, Theorem 1.1] does not depend on the specific choice of the sequence
$b_n$
, but it is enough that 
for every
$n \in \mathbb {N}$
so that the length of the interval
$[k/b_n, (k+1)/b_n]$
goes to
$0$
faster than
$2^{-n}$
as
$n \to + \infty $
. This concludes the proof of the first claim.
(2) Let
$([0,1), \mathcal {B}([0,1)), \lambda ^1, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
be the
${\mathfrak {N}}$
-refined standard Borel probability space of Example 3.2 with
$c=1$
. Then, for every
$\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
, there exist a strictly increasing sequence
$(N_n)_n \subset \mathbb {N}$
and maps
$g_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
such that, for every separable Banach spaces
$\mathsf {Z}, \mathsf {Z}'$
and every
$Z \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z})$
,
$Z' \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z}')$
, it holds
$$\begin{align*}(Z \otimes Z')_\sharp (\boldsymbol{i}_{[0,1)}, g_n)_\sharp \lambda^1 \to (Z\otimes Z')_\sharp \boldsymbol{\gamma} \ {in}\ \mathcal{P}(\mathsf{Z}\times \mathsf{Z}').\end{align*}$$
Let
$\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
, and let
$(g_n)_n$
be the sequence given by claim (1) for
$\boldsymbol {\gamma }$
. Let
$\mathsf {Z}$
and
$\mathsf {Z}'$
be separable Banach spaces, and let
$Z \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z})$
,
$Z' \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z}')$
. Observe that for every
$\varepsilon>0$
, there exists a compact set
$K_\varepsilon \subset [0,1)$
such that the restrictions of Z and
$Z'$
to
$K_\varepsilon $
are continuous in
$K_\varepsilon $
and
$\lambda ^1([0,1)\setminus K_\varepsilon )<\varepsilon $
, so that, setting
$\gamma _n:=(\boldsymbol {i}_{[0,1)}, g_n)_\sharp \lambda ^1$
,
$n \in \mathbb {N}$
, we have that
$\gamma _n([0,1)^{2}\setminus K_\varepsilon ^{2})\le 2\varepsilon $
for every
$n\in \mathbb {N}$
. By [Reference Ambrosio, Gigli and Savaré3, Proposition 5.1.10] and claim (1),
$(Z\otimes Z')_\sharp (\boldsymbol {i}_{[0,1)}, g_n)_\sharp \lambda ^1 \to (Z\otimes Z')_\sharp \boldsymbol {\gamma } \text { in } \mathcal {P}(\mathsf {Z}\times \mathsf {Z}')$
.
(3) Conclusion. Let
$\boldsymbol {\gamma } \in \Gamma (\mathbb {P}, \mathbb {P})$
, and let
$\varphi :\Omega \to [0,1)$
and
$\psi : [0,1) \to \Omega $
be the maps given by Proposition 3.12 for the
${\mathfrak {N}}$
-refined standard Borel probability spaces
$(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak P_N)_{N \in {\mathfrak {N}}})$
and
$([0,1), \mathcal {B}([0,1)), \lambda ^1, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
, where the latter is as in Example 3.2 with
$c=1$
. If we define
$\boldsymbol {\gamma }':=(\varphi \otimes \varphi )_\sharp \boldsymbol {\gamma }$
, we have that
$\boldsymbol {\gamma }' \in \Gamma (\lambda ^1, \lambda ^1)$
so that we can find a strictly increasing sequence
$(N_n)_n \subset \mathbb {N}$
and maps
$g^{\prime }_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
as in step (2). Let us define
$$\begin{align*}g_n:= \psi \circ g^{\prime}_n \circ \varphi, \quad n \in \mathbb{N}.\end{align*}$$
Then, up to change each
$g_n$
on a
$\mathbb {P}$
-negligible set of points, we can assume that
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{b_{N_n}})$
. Let
$\mathsf {Z}$
and
$\mathsf {Z}'$
be separable Banach spaces, and let
$Z \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z})$
,
$Z' \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z}')$
. If we define
$Z_{0}:=Z \circ \psi $
and
$Z^{\prime }_{0}:=Z' \circ \psi $
, we get that
$Z_{0} \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1); \mathsf {Z})$
,
$Z_{0}' \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1); \mathsf {Z}')$
. By step (2), we thus get
$$\begin{align*}(Z_{0}\otimes Z_{0}')_\sharp (\boldsymbol{i}_{[0,1)}, g^{\prime}_n)_\sharp \lambda^1 \to (Z_{0}\otimes Z_{0}')_\sharp \boldsymbol{\gamma}' \text{ in } \mathcal{P}(\mathsf{Z}\times \mathsf{Z}'), \end{align*}$$
which is equivalent to (3.12).
Remark 3.14 In the setting of Theorem 3.13, let
$\varphi :\mathsf {Z}\to [0,+\infty )$
,
$\varphi ':\mathsf {Z}'\to [0,+\infty )$
be Borel functions.
Setting
$$\begin{align*}\psi(z,z')=\varphi(z)+\varphi'(z'), \quad \text{ for every } (z,z') \in \mathsf{Z} \times \mathsf{Z}',\end{align*}$$
then we have for every
$n\in \mathbb {N}$
,
$$ \begin{align*} \int \psi \,\mathrm{d} (Z \otimes Z')_\sharp (\boldsymbol{i}_{\Omega}, g_n)_{\sharp}\mathbb{P} &= \int \psi(Z,Z'\circ g_n)\,\mathrm{d} \mathbb{P}= \int \Big(\varphi(Z)+\varphi'(Z'\circ g_n)\Big)\,\,\mathrm{d} \mathbb{P} \\&= \int \varphi(Z)\,\mathrm{d}\mathbb{P}+ \int \varphi'(Z')\,\mathrm{d}\mathbb{P} \\&= \int \varphi(Z(x_1))\,\mathrm{d}\boldsymbol{\gamma}(x_1,x_{2})+ \int \varphi'(Z'(x_{2}))\,\mathrm{d}\boldsymbol{\gamma}(x_1,x_{2}) \\&= \int \psi(Z(x_1),Z'(x_{2}))\, \mathrm{d}\boldsymbol{\gamma}(x_1,x_{2})= \int \psi \,\mathrm{d} (Z\otimes Z')_\sharp \boldsymbol{\gamma}. \end{align*} $$
As a consequence, if
$\mathsf {Z}=\mathsf {Z}'=\mathsf {X}$
for a separable Banach space
$\mathsf {X}$
and
$Z,Z' \in L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
,
$p \in [1,+\infty )$
, then the convergence in (3.12) holds in
$\mathcal {P}_p(\mathsf {X}^{2})$
. To prove this, it suffices to apply (3.11) and choose
$\psi (z,z'):= |z|_{\mathsf {X}}^{p} + |z'|_{\mathsf {X}}^{p}$
,
$z,z' \in \mathsf {X}$
, in the above identity.
We deduce two important applications.
Corollary 3.15 Let
$(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be an
${\mathfrak {N}}$
-refined standard Borel probability space. Then, for every
$\boldsymbol {\gamma } \in \Gamma (\mathbb {P}, \mathbb {P})$
, there exist a totally ordered strictly increasing sequence
$(N_n)_n \subset {\mathfrak {N}}$
and maps
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that, for every Polish topology
$\tau $
on
$\Omega $
generating
${\mathcal {B}}$
, it holds
$$\begin{align*}(\boldsymbol{i}_{\Omega}, g_n)_{\sharp}\mathbb{P} \to \boldsymbol{\gamma} \text{ in } \mathcal{P}(\Omega \times \Omega, \tau \otimes \tau),\end{align*}$$
where
$\tau \otimes \tau $
is the product topology on
$\Omega \times \Omega $
.
Proof By Theorem 3.13 and Remark 3.14, we have the existence of a strictly increasing sequence
$(N_n)_n \subset \mathbb {N}$
and maps
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that, choosing the separable Hilbert space
$\mathbb {R}$
, we get
$$\begin{align*}(\varphi_1\otimes \varphi_{2})_\sharp (\boldsymbol{i}_{\Omega}, g_n)_{\sharp}\mathbb{P} \to (\varphi_1\otimes \varphi_{2})_\sharp \boldsymbol{\gamma} \text{ in } \mathcal{P}_{2}(\mathbb{R}^{2}) \end{align*}$$
for every
$\varphi _1, \varphi _{2} \in \mathrm {C}_b(\Omega , \tau ) \subset L^{2}(\Omega ,{\mathcal {B}}, \mathbb {P}; \mathbb {R})$
. Since the range of
$\varphi _i$
is bounded and thus relatively compact, by the
$\mathcal {P}(\mathbb {R}^{2})$
convergence, we get that
$$\begin{align*}\int_{\Omega \times \Omega} h(\varphi_1(\omega_1), \varphi_{2}(\omega_{2})) \,\mathrm{d} \boldsymbol{\gamma}_n(\omega_1, \omega_{2}) \to \int_{\Omega \times \Omega} h(\varphi_1(\omega_1), \varphi_{2}(\omega_{2})) \,\mathrm{d} \boldsymbol{\gamma}(\omega_1, \omega_{2})\end{align*}$$
for every continuous function
$h: \mathbb {R}^{2} \to \mathbb {R}$
where
$\boldsymbol {\gamma }_n = (\boldsymbol {i}_{\Omega }, g_n)_{\sharp}\mathbb {P}$
,
$n \in \mathbb {N}$
. Choosing
$h(x,y):= xy$
, we get that
$$ \begin{align} \int_{\Omega \times \Omega} \varphi_1(\omega_1) \varphi_{2}(\omega_{2}) \,\mathrm{d} \boldsymbol{\gamma}_n(\omega_1, \omega_{2}) \to \int_{\Omega \times \Omega} \varphi_1(\omega_1) \varphi_{2}(\omega_{2}) \,\mathrm{d} \boldsymbol{\gamma}(\omega_1, \omega_{2}) \quad \forall \varphi_1, \varphi_{2} \in \mathrm{C}_b(\Omega, \tau). \end{align} $$
Let
$\mathcal {A} \subset \mathrm {C}_b(\Omega , \tau )$
be a unital subalgebra whose induced initial topology on
$\Omega $
coincides with
$\tau $
(e.g., the subset of
$\mathsf {d}$
-Lipschitz continuous and bounded functions for a complete distance
$\mathsf {d}$
inducing
$\tau $
). It is easy to check that
$$\begin{align*}\mathcal{A} \otimes \mathcal{A} := \left \{ \sum_{i=1}^n \varphi_1^i \otimes \varphi_{2}^i \mid (\varphi_1^i)_{i=1}^n, (\varphi_{2}^i)_{i=1}^n \subset \mathcal{A}, \, n \in \mathbb{N} \right \} \subset \mathrm{C}_b(\Omega \times \Omega, \tau \otimes \tau) \end{align*}$$
is a unital subalgebra whose induced initial topology on
$\Omega \times \Omega $
coincides with
$\tau \otimes \tau $
. By (3.15), we thus have that
$$\begin{align*}\int_{\Omega \times \Omega} \varphi \,\mathrm{d} \boldsymbol{\gamma}_n \to \int_{\Omega \times \Omega} \varphi \,\mathrm{d} \boldsymbol{\gamma} \quad \forall \varphi \in \mathcal{A} \otimes \mathcal{A}.\end{align*}$$
We conclude by [Reference Savaré and Sodini31, Lemma 2.3].
The second part of the following corollary represents a sort of extension of the known result in [Reference Cardaliaguet15, Lemma 6.4] (cf. also [Reference Carmona and Delarue16, Lemma 5.23, p. 379]) to the class of pairs
$(X,Y)$
of random variables, where X and Y take values on possibly different separable Banach spaces, with possibly different p-integrability. Whenever the joint distribution of two pairs
$(X,Y),(X',Y')$
belonging to such a class is equal, we are able to prove the existence of a sequence of measure-preserving maps giving the desired strong approximation result for both the components.
Corollary 3.16 Let
$(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be an
${\mathfrak {N}}$
-refined standard Borel probability space, let
$\mathsf {Z}$
and
$\mathsf {Z}'$
be separable Banach spaces, and let
$Z \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z})$
,
$Z' \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z}')$
. Then, for every
$\boldsymbol {\mu }\in \Gamma (Z_{\sharp}\mathbb {P},Z^{\prime }_{\sharp}\mathbb {P})$
, there exist a totally ordered strictly increasing sequence
$(N_n)_n \subset {\mathfrak {N}}$
and maps
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that
$$ \begin{align} (Z,Z'\circ g_n)_{\sharp}\mathbb{P} \to \boldsymbol{\mu} \text{ in } \mathcal{P}(\mathsf{Z}\times \mathsf{Z}'). \end{align} $$
In particular, if
$\mathsf {X}$
and
$\mathsf {Y}$
are separable Banach spaces,
$X,X' \in L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
,
$Y,Y' \in L^q(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Y})$
,
$p,q \in [1,+\infty )$
, and
$(X,Y)_{\sharp}\mathbb {P}=(X',Y')_{\sharp}\mathbb {P}$
, then there exist a totally ordered strictly increasing sequence
$(N_n)_n \subset {\mathfrak {N}}$
and maps
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that
$X'\circ g_n\to X$
in
$L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
and
$Y'\circ g_n\to Y$
in
$L^q(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Y})$
as
$n\to \infty $
.
Proof Let
$\mu :=Z_{\sharp}\mathbb {P}$
and
$\mu ':=Z^{\prime }_{\sharp}\mathbb {P}$
; let us first observe that there exists
$\boldsymbol {\gamma }\in \Gamma ({\mathbb {P}},{\mathbb {P}})$
such that
$(Z\otimes Z')_\sharp \boldsymbol {\gamma }=\boldsymbol {\mu }$
. In fact, we can disintegrate
$\mathbb {P}$
w.r.t. Z and
$\mu $
(see, e.g., [Reference Ambrosio, Gigli and Savaré3, Theorem 5.3.1] for details on the disintegration theorem), obtaining a Borel family of measures
$(\theta _z)_{z\in \mathsf {Z}}\subset \mathcal {P}(\Omega )$
such that
$\theta _z$
is concentrated on
$Z^{-1}(z)$
for
$\mu $
-a.e.
$z \in \mathsf {Z}$
and
$\mathbb {P}=\int \theta _z \,\mathrm {d}\mu (z)$
; similarly, we can also find
$(\theta ^{\prime }_{z'})_{z'\in \mathsf {Z}'}\subset \mathcal {P}(\Omega )$
such that
$\theta _{z'}^{\prime }$
is concentrated on
$(Z')^{-1}(z')$
for
$\mu '$
-a.e.
$z' \in \mathsf {Z}'$
and
$\mathbb {P} = \int \theta ^{\prime }_{z'}\,\mathrm {d}\mu '(z')$
. We can thus define
$\boldsymbol {\gamma }:=\int (\theta _{z}\otimes \theta ^{\prime }_{z'})\,{\mathrm {d}} \boldsymbol {\mu }(z,z')\in {\mathcal {P}}({\Omega }\times {\Omega })$
, and it is immediate to check that
$(Z\otimes Z')_\sharp \boldsymbol {\gamma }=\boldsymbol {\mu }$
since for every function
$\varphi _1\in \mathrm {C}_b(\mathsf {Z})$
,
$\varphi _{2}\in \mathrm {C}_b(\mathsf {Z'})$
,
$$ \begin{align*} &\int \varphi_1(Z(\omega))\varphi_{2}(Z'(\omega'))\,\mathrm{d}\boldsymbol{\gamma}(\omega,\omega')\\ &= \int \bigg(\int \varphi_1(Z(\omega))\varphi_{2}(Z'(\omega'))\,\mathrm{d}\theta_{z}(\omega)\,\mathrm{d}\theta^{\prime}_{z'}(\omega') \bigg)\,\mathrm{d} \boldsymbol{\mu}(z,z') \\&= \int \int \varphi_1(Z(\omega))\,\mathrm{d}\theta_z(\omega) \int\varphi_{2}(Z'(\omega'))\,\mathrm{d}\theta^{\prime}_{z'}(\omega') \,\mathrm{d} \boldsymbol{\mu}(z,z') \\&= \int \Big( \varphi_1(z) \varphi_{2}(z')\Big) \,\mathrm{d} \boldsymbol{\mu}(z,z'). \end{align*} $$
Notice also that it is enough to verify that
$(Z,Z')_{\sharp}\mathbb {P}$
and
$\boldsymbol {\gamma }$
have the same integral for every function of the form
$\varphi _1 \otimes \varphi _{2}$
as above to conclude that the two measures coincide (see, e.g., the proof of the above Corollary 3.15). We can then apply (3.12) and obtain (3.16).
Let us show the last part of the statement: we take
$\mathsf {Z}=\mathsf {Z}':=\mathsf {X} \times \mathsf {Y}$
and, by (3.16) with
$Z:=(X,Y)$
,
$Z':=(X',Y')$
and
$\boldsymbol {\mu }:=(\boldsymbol {i}_{\mathsf {X} \times \mathsf {Y}},\boldsymbol {i}_{\mathsf {X} \times \mathsf {Y}})_\sharp (X,Y)_{\sharp}\mathbb {P}$
, we have that
$$\begin{align*}(X,Y,X'\circ g_n,Y'\circ g_n)_{\sharp}\mathbb{P} \to \boldsymbol{\mu} \text{ in } \mathcal{P}((\mathsf{X} \times \mathsf{Y})^{2}). \end{align*}$$
We thus have that
$(X,X'\circ g_n)_{\sharp}\mathbb {P} \to (\boldsymbol {i}_{\mathsf {X}},\boldsymbol {i}_{\mathsf {X}})_\sharp X_{\sharp}\mathbb {P}$
in
$\mathcal {P}(\mathsf {X}^{2})$
. By Remark 3.14 with
$\psi ((x,y),(x',y'))= |x|_{\mathsf {X}}^{p} + |x'|_{\mathsf {X}}^{p}$
,
$x,x \in \mathsf {X}, y,y' \in \mathsf {Y}$
, we get, also using (3.11), that
$(X,X'\circ g_n)_{\sharp}\mathbb {P} \to (\boldsymbol {i}_{\mathsf {X}},\boldsymbol {i}_{\mathsf {X}})_\sharp X_{\sharp}\mathbb {P}$
in
$\mathcal {P}_p(\mathsf {X}^{2})$
. As a consequence (see, e.g., [Reference Ambrosio, Gigli and Savaré3, Proposition 7.1.5 and Lemma 5.1.7]), we get
$$ \begin{align*} \lim_{n\to\infty} \int |X-X'\circ g_n|^{p}\,\mathrm{d}\mathbb{P} &= \lim_{n\to\infty} \int |x-x'|^{p}\,\mathrm{d}\big((X,X'\circ g_n)_{\sharp}\mathbb{P})(x,x')\\ &= \int |x-x'|^{p}\,\mathrm{d}((\boldsymbol{i}_{\mathsf{X}},\boldsymbol{i}_{\mathsf{X}})_\sharp X_{\sharp}\mathbb{P})(x,x')\\ &=0. \end{align*} $$
The proof for Y and
$Y'$
is identical.
Remark 3.17 In the same setting of Corollary 3.16 and similarly to Remark 3.14, if
$\mathsf {Z}=\mathsf {Z}'=\mathsf {X}$
for a separable Banach space
$\mathsf {X}$
and
$X,X' \in L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
,
$p \in [1,+\infty )$
, then (3.11) gives that the convergence in (3.16) holds in
$\mathcal {P}_p(\mathsf {X}^{2})$
,
As a byproduct, we recover the following important result (see, e.g., [Reference Gangbo and Tudorascu21, Lemma 3.13] for a statement in case
$p=2$
and
$\mathsf {X}=\mathbb {R}^d$
), which is also related to the equivalence between the Monge and the Kantorovich formulations of Optimal Transport problems [Reference Ambrosio2, Theorems 2.1 and 9.3], [Reference Pratelli27, Theorem B].
Proposition 3.18 Let
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic probability measure
$\mathbb {P}$
, let
$\mathsf {X}$
be a separable Banach space, and let
$p\in [1,+\infty )$
. If
$\mu , \nu \in \mathcal {P}_p(\mathsf {X})$
and
$X \in L^{p}(\Omega , {\mathcal {B}},\mathbb {P}; \mathsf {X})$
is s.t.
$X_{\sharp}\mathbb {P} = \mu $
, then, for every
$\varepsilon>0$
, there exists
$Y \in L^{p}(\Omega , {\mathcal {B}},\mathbb {P}; \mathsf {X})$
s.t.
$Y_{\sharp}\mathbb {P} = \nu $
and
$$\begin{align*}|X-Y|_{L^{p}(\Omega {\mathcal{B}},\mathbb{P}; \mathsf{X})} \le W_p(\mu, \nu) + \varepsilon.\end{align*}$$
Proof Let us consider the
${\mathfrak {N}}$
-refined standard Borel probability space
$(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
with
${\mathfrak {N}} =(2^k)_{k \in \mathbb {N}}$
; let
$\boldsymbol {\mu } \in \Gamma _o(\mu , \nu )$
and let
$X'\in L^{p}(\Omega ,{\mathcal {B}},\mathbb {P}; \mathsf {X})$
be such that
$X^{\prime }_{\sharp}\mathbb {P}=\nu $
. By Corollary 3.16 and Remark 3.17, there exist a strictly increasing sequence
$(N_n)_n \subset {\mathfrak {N}}$
and maps
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that
$$ \begin{align*} (X,X'\circ g_n)_{\sharp}\mathbb{P} \to \boldsymbol{\mu} \text{ in } \mathcal{P}_p(\mathsf{X}^{2}). \end{align*} $$
We have
$$ \begin{align*} \lim_{n\to\infty} \int |X-X'\circ g_n|^{p}\,\mathrm{d}\mathbb{P} &= \lim_{n\to\infty} \int |x-y|^{p}\,\mathrm{d}\big((X,X'\circ g_n)_{\sharp}\mathbb{P})(x,y)\\&=\int |x-y|^{p}\,\mathrm{d}\boldsymbol{\mu}(x,y) =W_p^{p}(\mu,\nu). \end{align*} $$
Thus, given
$\varepsilon>0$
, it is always possible to find
$n \in \mathbb {N}$
sufficiently large such that
$Y:=X' \circ g_n$
satisfies the thesis.
4 Monotone-dissipative operators and Lipschitz maps in
$L^{p}$
-spaces invariant by measure-preserving transformations
Let
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic probability measure
$\mathbb {P}$
(see Definition 3.1). We denote by
$\mathrm {S}(\Omega )$
the class of
${\mathcal {B}}$
-
${\mathcal {B}}$
-measurable maps
$g:\Omega \to \Omega $
which are essentially injective and measure-preserving, i.e., there exists a full
$\mathbb {P}$
-measure set
$\Omega _{0} \in {\mathcal {B}}$
such that g is injective on
$\Omega _{0}$
and
$g_{\sharp}\mathbb {P}=\mathbb {P}$
. If
$g\in \mathrm {S}(\Omega )$
, there exists
$g^{-1}\in \mathrm {S}(\Omega )$
(defined up to a
$\mathbb {P}$
-negligible set) such that
$g^{-1}\circ g=g\circ g^{-1}=\boldsymbol {i}_\Omega \mathbb {P}$
-a.e. in
$\Omega $
.
Consider two separable Banach spaces
$\mathsf {X},\mathsf {Y}$
and fix exponents
$p,q\in [1,+\infty )$
. We set
$$ \begin{align} \mathcal{X}:=L^{p}(\Omega, {\mathcal{B}}, \mathbb{P};\mathsf{X}),\quad \mathcal{Y}:=L^q(\Omega, {\mathcal{B}}, \mathbb{P};\mathsf{Y}). \end{align} $$
Notice that for every
$g\in \mathrm {S}(\Omega )$
, the pullback transformation
$g^{*}:\mathcal {X}\mapsto \mathcal {X}$
sending X to
$X \circ g$
is a linear isometry of
$\mathcal {X}$
: in particular,
$$ \begin{align} X_n\to X\text{ strongly in}\ \mathcal{X} \quad&\Longrightarrow \quad g^{*} X_n\to g^{*} X\text{ strongly in}\ \mathcal{X}, \end{align} $$
$$ \begin{align} X_n\to X\text{ weakly in}\ \mathcal{X} \quad&\Longrightarrow \quad g^{*} X_n\to g^{*} X\text{ weakly in}\ \mathcal{X}. \end{align} $$
The aim of this section is to study properties of maps and sets/operators, defined on these particular spaces, which are invariant by measure-preserving transformations. We will also apply the results of Section 2 to this particular setting. The interest on such kinds of properties is made evident by the implications in the study of dissipative evolutions in Wasserstein spaces via Lagrangian representations (cf. [Reference Cavagnari, Savaré and Sodini17]).
Definition 4.1 (Invariant sets and maps)
We say that a set
$\boldsymbol {B}\subset \mathcal {X}\times \mathcal {Y}$
is invariant by measure-preserving isomorphisms if for every
$g \in \mathrm {S}(\Omega )$
it holds
$$ \begin{align} (X,Y) \in \boldsymbol{B} \quad \Longrightarrow\quad (g^{*}X,g^{*}Y)=(X\circ g,Y\circ g) \in \boldsymbol{B}, \end{align} $$
where, with a slight abuse of notation, we denote with the same symbol
$g^{*}$
both the pullback transformation induced by g on
$\mathcal {X}$
and on
$\mathcal {Y}$
. A set
$\boldsymbol {B} \subset \mathcal {X}\times \mathcal {Y}$
is law invariant if it holds
$$ \begin{align} (X,Y) \in \boldsymbol{B},\quad (X',Y')\in\mathcal{X}\times\mathcal{Y}, \quad (X,Y)_{\sharp}\mathbb{P}=(X',Y')_{\sharp}\mathbb{P}\quad \Longrightarrow\quad (X',Y') \in \boldsymbol{B}. \end{align} $$
A (single valued) operator
${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {Y}$
is invariant by measure-preserving isomorphisms (resp. law invariant) if its graph in
$\mathcal {X}\times \mathcal {Y}$
is invariant by measure preserving isomorphisms (resp. law invariant).
It is easy to check that a law invariant set or operator is also invariant by measure-preserving isomorphisms. It is also immediate to check that an operator
${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {Y}$
is invariant by measure-preserving isomorphisms if for every
$g\in \mathrm {S}(\Omega )$
and every
$X\in \mathrm {D}({\boldsymbol {L}})$
it holds
$$ \begin{align} X\circ g\in \mathrm{D}({\boldsymbol{L}}),\quad {\boldsymbol{L}}(X\circ g)= {\boldsymbol{L}}(X)\circ g. \end{align} $$
Similarly,
${\boldsymbol {L}}$
is law invariant if for every
$X\in \mathrm {D}({\boldsymbol {L}}),\ X'\in \mathcal {X},\ Y'\in \mathcal {Y}$
,
$$ \begin{align} (X,{\boldsymbol{L}} X)_{\sharp}\mathbb{P}=(X',Y')_{\sharp}\mathbb{P}\quad \Longrightarrow\quad X'\in \mathrm{D}({\boldsymbol{L}}),\quad Y'={\boldsymbol{L}} X'. \end{align} $$
Remark 4.1 Notice that, when
$\mathsf {Y}=\mathsf {X}^{*}$
are reflexive,
$p>1$
, and
$q=p^{*}$
is the conjugate exponent of p, then
$\mathcal {Y}=\mathcal {X}^{*}$
and the notion of invariance by measure-preserving isomorphisms for
$\boldsymbol {B}\subset \mathcal {X}\times \mathcal {Y}$
coincides with the
$\mathsf {G}$
-invariance of Definition 2.1,
$\mathsf {G}$
being the group of isometric isomorphisms induced by
$\mathrm {S}(\Omega )$
via
$g^{*}:\mathcal {X}\times \mathcal {X}^{*} \to \mathcal {X}\times \mathcal {X}^{*}$
with
$g^{*}(X,V) = (X\circ g,V\circ g)$
for every
$(X,V) \in \mathcal {X}\times \mathcal {X}^{*}$
and every
$g \in \mathrm {S}(\Omega )$
.
Let us denote by
$\iota :\mathcal {X}\to \mathcal {P}_p(\mathsf {X})$
the push-forward operator,
$\iota (X):=X_{\sharp}\mathbb {P}$
(cf. (3.1)). We frequently use the notation
$\iota _X=\iota (X)$
. The map
$\iota $
induces a one-to-one correspondence between subsets in
$\mathcal {P}_p(\mathsf {X})$
(see (3.9)) and law invariant subsets of
$\mathcal {X}$
.
As a first result, we show that for closed sets and continuous operators the two notions of invariance are in fact equivalent.
Proposition 4.2 (Closed sets invariant by m.p.i. are law invariant)
If
$\boldsymbol {B}\subset \mathcal {X}\times \mathcal {Y}$
is invariant by measure-preserving isomorphisms, then its closure
$\overline {\boldsymbol {B}}$
is also law invariant. In particular, a closed set of
$\mathcal {X}\times \mathcal {Y}$
is law invariant if and only if it is invariant by measure-preserving isomorphisms and if
${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to {\mathcal {Y}}$
is a continuous operator invariant by measure-preserving isomorphisms and
$\mathrm {D}({\boldsymbol {L}})$
is closed, then
${\boldsymbol {L}}$
is also law invariant.
Proof Let us first observe that if
$\boldsymbol {B}$
is invariant by measure-preserving isomorphisms, then
$\overline {\boldsymbol {B}}$
has the same property, since for every
$g\in \mathrm {S}(\Omega )$
the pullback transformation
$g^{*}$
is an isometry in
$\mathcal {X}$
and in
$\mathcal {Y}$
. Let us now suppose that
$\boldsymbol {B}$
is closed and invariant by measure-preserving isomorphisms,
$(X,Y)\in \boldsymbol {B}$
,
$(X',Y')\in \mathcal {X}\times \mathcal {Y}$
with
$(X,Y)_{\sharp}\mathbb {P}=(X',Y')_{\sharp}\mathbb {P}$
. We can apply Corollary 3.16 and find a sequence of measure-preserving isomorphisms
$g_n\in \mathrm {S}(\Omega )$
such that
$(X,Y)\circ g_n\to (X',Y')$
in
$\mathcal {X}\times \mathcal {Y}$
. Since
$(X,Y)\circ g_n\in \boldsymbol {B}$
and
$\boldsymbol {B}$
is closed, we deduce that
$(X',Y')\in \boldsymbol {B}$
as well.
The case of continuous operators then follows by the fact that the graph of a continuous operator is closed.
Remark 4.3 In light of Proposition 4.2, if a subset
$\boldsymbol {B} \subset \mathcal {X}\times \mathcal {Y}$
(resp. an operator
${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {Y}$
) is closed (resp. continuous and
$\mathrm {D}({\boldsymbol {L}})$
is closed), we use the simplified terminology invariant, whenever
$\boldsymbol {B}$
(resp.
${\boldsymbol {L}}$
) is law invariant or invariant by measure-preserving isomorphisms, being these two notions equivalent.
As an application of the results in Section 2, we obtain the following extension results.
Theorem 4.4 (Maximal extensions of monotone operators invariant by measure-preserving isomorphisms)
Let
$\mathsf {X}$
be a separable and reflexive Banach space,
$p\in (1,\infty )$
, and
$\mathcal {X}:=L^{p}(\Omega ,{\mathcal {B}}, \mathbb {P};\mathsf {X})$
. If
${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
is a monotone operator invariant by measure-preserving isomorphisms, then there exists a maximal monotone extension of
${\boldsymbol {A}}$
which is invariant by measure-preserving isomorphisms (and therefore also law invariant) whose domain is contained in
$\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right ).$
Proof The thesis follows by applying Theorem 2.5 and Remark 4.1. Recall also that if
${\boldsymbol {A}}$
is maximal monotone, then it is closed (see, e.g., [Reference Barbu6, Proposition 2.1]); hence, we can apply Proposition 4.2.
Theorem 4.5 (Extension of Lipschitz and
$\lambda $
-dissipative invariant graphs)
Assume
${p=2}$
, and let
$\mathsf {X}$
be a separable and Hilbert space. The following hold:
-
(1) If
${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {X}$
is an L-Lipschitz function invariant by measure-preserving isomorphisms, then there exists an L-Lipschitz extension
$ {\hat {\boldsymbol {L}}}:\mathcal {X}\to \mathcal {X}$
, defined on the whole
$\mathcal {X}$
which is invariant by measure-preserving isomorphisms. -
(2) If
$\boldsymbol {B} \subset \mathcal {X} \times \mathcal {X}$
is a
$\lambda $
-dissipative operator which is invariant by measure-preserving isomorphisms, then there exists a maximal
$\lambda $
-dissipative extension
$\hat {\boldsymbol {B}}$
of
$\boldsymbol {B}$
which is invariant by measure-preserving isomorphisms (and therefore also law invariant) whose domain is contained in
$\overline {\operatorname {co}}\left (\mathrm {D}(\boldsymbol {B})\right ).$
Proof The assertion is an immediate application of Theorems 2.11 and 2.7, choosing
$\mathcal {H}:=\mathcal {X}$
and
$\mathsf {G}_{\mathcal {H}}$
as the group of isometric isomorphisms induced by
$\mathrm {S}(\Omega )$
via
$g^{*}:\mathcal {X} \to \mathcal {X}$
with
$g^{*}X = X\circ g$
for every
$X \in \mathcal {X}$
and every
$g \in \mathrm {S}(\Omega )$
(cf. Remark 4.1). Notice that
$\boldsymbol {B}$
is closed being maximal dissipative, hence law invariant by Proposition 4.2.
We conclude this section with some useful representation results for various classes of law invariant transformations.
Given a set
$D\subset \mathcal {P}_p(\mathsf {X})$
, we set
$$ \begin{align} \mathcal{S}(\mathsf{X},D):=\Big\{(x,\mu)\in \mathsf{X}\times D\,:\,x\in \operatorname{\mathrm{supp}}(\mu)\Big\}, \end{align} $$
and we just write
$\mathcal {S}(\mathsf {X})=\mathcal {S}(\mathsf {X},\mathcal {P}_p(\mathsf {X}))$
. The set
$\mathcal {S}(\mathsf {X})$
is of
$G_\delta $
type (see [Reference Fornasier, Savaré and Sodini20, Formula (4.3)]) so that
$\mathcal {S}(\mathsf {X},D)$
is a Borel set, if D is Borel.
We state a first result on uniqueness of a representation of a single-valued operator
${\boldsymbol {L}}:\mathcal {X}\to \mathcal {Y}$
by a map from
$\mathcal {S}(\mathsf {X})$
to
$\mathsf {Y}$
. We then state existence (and uniqueness) of such map-representation when
${\boldsymbol {L}}$
is Lipschitz continuous and invariant, showing also further properties inherited by such map representation. Finally, we will go back to the case of (possibly multivalued) maximal
$\lambda $
-dissipative operators in the final Theorem 4.12.
Lemma 4.6 Let
${\boldsymbol {L}}: \mathrm {D}({\boldsymbol {L}}) \to \mathcal {Y}$
be a map defined in
$\mathrm {D}({\boldsymbol {L}}) \subset \mathcal {X}$
. If
$\boldsymbol {f}_i: \mathcal {S}(\mathsf {X}, \iota (\mathrm {D}({\boldsymbol {L}})) \to \mathsf {Y}$
,
$i=1,2$
, satisfy
-
•
$\boldsymbol {f}_i(\cdot , \mu )$
is continuous for every
$\mu \in \iota (\mathrm {D}({\boldsymbol {L}}))$
, -
• for every
$X\in \mathrm {D}({\boldsymbol {L}})$
${\boldsymbol {L}} X(w)=\boldsymbol {f}_i(X(w),X_{\sharp}\mathbb {P})$
for a.e.
$\omega \in \Omega $
,
then
$\boldsymbol {f}_1=\boldsymbol {f}_{2}$
.
Proof Let
$(x,\mu ) \in \mathcal {S}(\mathsf {X}, \iota (\mathrm {D}({\boldsymbol {L}}))$
. Since
$\mu \in \iota (\mathrm {D}({\boldsymbol {L}}))$
, we can find (a representative of)
$X \in \mathrm {D}({\boldsymbol {L}})$
such that
$X_{\sharp}\mathbb {P}= \mu $
and a full
$\mathbb {P}$
-measure set
$\Omega _{0} \subset \Omega $
such that
$$\begin{align*}{\boldsymbol{L}} X(\omega)=\boldsymbol{f}_1(X(\omega),X_{\sharp}\mathbb{P}) = \boldsymbol{f}_{2}(X(\omega),X_{\sharp}\mathbb{P}) \text{ for every } \omega\in \Omega_{0}.\end{align*}$$
Since
$X(\Omega _{0})$
is dense in
$\operatorname {\mathrm {supp}}(\mu )$
, we can find
$(\omega _n)_n \subset \Omega _{0}$
such that
$X(\omega _n) \to x$
. Using the continuity of
$\boldsymbol {f}_i(\cdot , \mu )$
, we can write the above equality for
$\omega =\omega _n$
and then pass to the limit as
$n \to + \infty $
obtaining that
$\boldsymbol {f}_1(x,\mu )=\boldsymbol {f}_{2}(x,\mu )$
.
In the following Theorem 4.7, we provide an important structural representation of invariant Lipschitz maps from
$\mathcal {X}$
to
$\mathcal {Y}$
. Similar kinds of problems have been considered in [Reference Carmona and Delarue16, Proposition 5.36].
Theorem 4.7 (Structure of invariant Lipschitz maps)
Let
$\mathsf {X},\mathsf {Y}$
be separable Banach spaces, and let
$\mathcal {X},\mathcal {Y}$
be as in (4.1).
-
(1) Let
${\boldsymbol {L}}: \mathcal {X} \to \mathcal {Y}$
be an L-Lipschitz map, invariant by measure-preserving isomorphisms. Then there exists a unique continuous map
${\boldsymbol {f}}_{{\boldsymbol {L}}}:\mathcal {S}(\mathsf {X}) \to \mathsf {Y}$
such that (4.9)
$$ \begin{align} \text{for every}\ X\in \mathcal{X},\quad {\boldsymbol{L}} X(\omega)={\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),X_{\sharp}\mathbb{P})\ \text{for a.e}.~\omega\in \Omega. \end{align} $$
Moreover,
${\boldsymbol {f}}_{{\boldsymbol {L}}} (\cdot , \mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {Y}$
is L-Lipschitz. -
(2) Let
$\mathsf {X}$
be a Hilbert space and
$p=2$
, let
$\mathrm {D}({\boldsymbol {L}}) \subset \mathcal {X}$
, and let
${\boldsymbol {L}}: \mathrm {D}({\boldsymbol {L}}) \to \mathcal {X}$
be an L-Lipschitz map, invariant by measure-preserving isomorphisms. Then there exists a unique continuous map
${\boldsymbol {f}}_{{\boldsymbol {L}}}:\mathcal {S}(\mathsf {X}, \iota (\mathrm {D}({\boldsymbol {L}}))\to \mathsf {X}$
such that (4.10)
$$ \begin{align} \text{for every}\ X\in \mathrm{D}({\boldsymbol{L}}),\quad {\boldsymbol{L}} X(\omega)={\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),X_{\sharp}\mathbb{P})\ \text{for a.e}.~\omega\in \Omega. \end{align} $$
Moreover,
${\boldsymbol {f}}_{{\boldsymbol {L}}} (\cdot , \mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is L-Lipschitz.
Proof We prove item (1). Let
${\mathfrak {N}}:= \{2^n \mid n \in \mathbb {N}\}$
, and let
$(\mathfrak {P}_N)_{N \in {\mathfrak {N}}}$
be an
${\mathfrak {N}}$
-segmentation of
$(\Omega , {\mathcal {B}}, \mathbb {P})$
as in Definition 3.3, whose existence is granted by Lemma 3.5. Let us define
$$\begin{align*}{\mathcal{B}}_n:= \sigma(\mathfrak{P}_{2^n}),\quad \mathcal{X}_n:= L^{p}(\Omega, {\mathcal{B}}_n, \mathbb{P}; \mathsf{X}), \quad \mathcal{Y}_n:= L^q(\Omega, {\mathcal{B}}_n, \mathbb{P}; \mathsf{Y}),\quad n \in \mathbb{N}.\end{align*}$$
We divide the proof in several steps.
(a) If
$X \in \mathcal {X}_m$
for some
$m \in \mathbb {N}$
, then (there exists a unique representative of)
${\boldsymbol {L}} X$
(that) belongs to
$\mathcal {Y}_m$
and
$$ \begin{align} |{\boldsymbol{L}} X(\omega')-{\boldsymbol{L}} X(\omega")|_{\mathsf{Y}}\le L|X(\omega')-X(\omega")|_{\mathsf{X}}\quad \text{for every }\omega',\omega"\in \Omega. \end{align} $$
Let
$\Omega ' \subset \Omega $
be a full
$\mathbb {P}$
-measure subset of
$\Omega $
where both (3.5) and Lemma 3.11 hold for the
$L^q(\Omega , {\mathcal {B}}, \mathbb {P};\mathsf {Y})$
function
${\boldsymbol {L}} X$
.
Let us fix
$k \in I_m:=\{0,\dots ,2^m-1\}$
and show that (a representative of)
${\boldsymbol {L}} X $
is constant on
$\Omega ^{\prime }_{m,k}:= \Omega _{m,k} \cap \Omega '$
, where
$\mathfrak {P}_{2^m} := \{\Omega _{m,k}\}_{k \in I_m}$
.
Let
$\omega ', \omega " \in \Omega ^{\prime }_{m,k}$
with
$\omega '\ne \omega "$
. For every
$n \in \mathbb {N}$
, there exist
$k(n;\omega '), k(n;\omega ") \in I_{n}$
such that
$\omega ' \in \Omega _{n,k(n;\omega ')}$
and
$\omega " \in \Omega _{n,k(n;\omega ")}$
. By Lemma 3.11, we know that for
$n \in \mathbb {N}$
sufficiently large
$\Omega _{n,k(n;\omega ')}, \Omega _{n,k(n;\omega ")} \subset \Omega _{m,k}$
and
$\Omega _{n,k(n;\omega ')} \cap \Omega _{n,k(n;\omega ")} = \emptyset $
. Thus, since
$\mathbb {P}(\Omega _{n,k(n;\omega ')})= \mathbb {P}(\Omega _{n,k(n;\omega ")})=2^{-n}$
for every
$n \in \mathbb {N}$
(see Definition 3.3), by Corollary 3.8, we can find a measure-preserving isomorphism
$g_n \in \mathrm {S}(\Omega )$
such that
$$\begin{align*}(g_n)_{\sharp}\mathbb{P} |_{\Omega_{n,k(n;\omega')}} = \mathbb{P} |_{\Omega_{n,k(n;\omega")}}\end{align*}$$
and
$g_n$
is the identity outside
$\Omega _{n,k(n;\omega ')} \cup \Omega _{n,k(n;\omega ")}$
. By (4.6) and by Lipschitz continuity of
${\boldsymbol {L}}$
, we have
$$\begin{align*}\left | {\boldsymbol{L}} X \circ g_n - {\boldsymbol{L}} X \right |_{\mathcal{Y}} \le L\left | X \circ g_n - X \right |_{\mathcal{X}}=0 \quad \text{for every integer}\ n\ \text{sufficiently large}, \end{align*}$$
since X is constant on the whole
$\Omega _{m,k}$
. This implies that
$$\begin{align*}2^{-n} \int_{\Omega_{n,k(n;\omega')}} {\boldsymbol{L}} X \,\mathrm{d} \mathbb{P} = 2^{-n} \int_{\Omega_{n,k(n;\omega")}} {\boldsymbol{L}} X \,\mathrm{d} \mathbb{P} \quad \text{eventually}. \end{align*}$$
By definition of conditional expectation, this means that
$$\begin{align*}\mathbb{E}_{\mathbb{P}} \left [ {\boldsymbol{L}} X \mid \sigma \left (\mathfrak{P}_{2^n} \right ) \right ] (\omega') = \mathbb{E}_{\mathbb{P}} \left [ {\boldsymbol{L}} X \mid \sigma \left (\mathfrak{P}_{2^n} \right ) \right ] (\omega") \quad \text{eventually.}\end{align*}$$
Passing to the limit as
$n \to + \infty $
, we get by (3.5) that
${\boldsymbol {L}} X(\omega ')={\boldsymbol {L}} X(\omega ")$
. This proves that
${\boldsymbol {L}} X$
is
$\mathbb {P}$
-almost everywhere constant on
$\Omega _{m,k}$
; being
$k \in I_m$
arbitrary, we can find a representative of
${\boldsymbol {L}} X$
belonging to
$\mathcal {Y}_m$
. If
$\omega ', \omega " \in \Omega $
and
$\omega ' \in \Omega _{m,i}$
,
$\omega "\in \Omega _{m,j}$
,
$i,j\in I_m$
, we choose as
$g \in \mathrm {S}(\Omega )$
a measure-preserving isomorphism induced by the permutation
$\sigma \in {\mathrm {Sym}(I_m)}$
that swaps i and j (see Corollary 3.7), so that we get by Lipschitz continuity of
${\boldsymbol {L}}$
that
$$\begin{align*}\frac 1{2^{(m-1)/2}} |{\boldsymbol{L}} X(\omega')-{\boldsymbol{L}} X(\omega")|_{\mathsf{Y}} \le L \frac 1{2^{(m-1)/2 }} |X(\omega')-X(\omega")|_{\mathsf{X}}\,, \end{align*}$$
which yields (4.11).
(b) For every
$X\in \mathcal {X}$
, there exists a unique L-Lipschitz map
$\boldsymbol {f}_X:\operatorname {\mathrm {supp}}(X_{\sharp}\mathbb {P})\to \mathsf {Y}$
such that
${\boldsymbol {L}} X(\omega ) = \boldsymbol {f}_{X}(X(\omega ))$
for
$\mathbb {P}$
-a.e.
$\omega $
.
Let
$X \in \mathcal {X}$
; setting
$X_n:=\mathbb {E}[X|{\mathcal {B}}_n]\in \mathcal {X}_n$
, by Theorem 3.9, we have
$X_n \to X$
(hence also
${\boldsymbol {L}} X_n \to {\boldsymbol {L}} X$
). Let us consider two representatives of
${\boldsymbol {L}} X$
and X, a full measure set
$\Omega _{0} \subset \Omega $
and a subsequence
$(X_{n_{k}})_{k}$
s.t.
$X_{n_{k}}(\omega ) \to X(\omega )$
and
${\boldsymbol {L}} X_{n_{k}}(\omega ) \to {\boldsymbol {L}} X (\omega )$
for every
$\omega \in \Omega _{0}$
. By (4.11), we have
$$\begin{align*}|{\boldsymbol{L}} X_n(\omega')-{\boldsymbol{L}} X_n(\omega) |_{\mathsf{Y}} \le L |X_n(\omega')-X_n(\omega)|_{\mathsf{X}} \text{ for every }\omega, \omega' \in \Omega, \, n \in \mathbb{N}. \end{align*}$$
Passing to the limit in the above inequality for every couple
$(\omega , \omega ') \in \Omega _{0}^{2}$
, we obtain that
$$\begin{align*}|{\boldsymbol{L}} X(\omega')-{\boldsymbol{L}} X(\omega) |_{\mathsf{Y}} \le L |X(\omega')-X(\omega)|_{\mathsf{X}} \text{ for every }\omega, \omega' \in \Omega_{0}. \end{align*}$$
This gives the existence of a (unique) L-Lipschitz function
$\boldsymbol {f}_X: \overline {X(\Omega _{0})}\to \mathsf {Y}$
s.t.
${\boldsymbol {L}} X(\omega ) = \boldsymbol {f}_{X}(X(\omega ))$
for every
$\omega \in \Omega _{0}$
. Notice that
$\overline {X(\Omega _{0})}\supset \operatorname {\mathrm {supp}}(X_{\sharp}\mathbb {P})$
.
(c) If
$X, X'\in \mathcal {X}$
with
$\mu =X_{\sharp}\mathbb {P}=X^{\prime }_{\sharp}\mathbb {P}$
, then
$\boldsymbol {f}_X=\boldsymbol {f}_{X'}$
on
$\operatorname {\mathrm {supp}}(\mu )$
. In particular, we can define
${\boldsymbol {f}}_{{\boldsymbol {L}}} (\cdot ,\mu ):=\boldsymbol {f}_X(\cdot )$
whenever
$\mu =X_{\sharp}\mathbb {P}$
.
By hypothesis, we have
$$ \begin{align} (X, {\boldsymbol{L}} X)_{\sharp}\mathbb{P} = (X', {\boldsymbol{L}} X')_{\sharp}\mathbb{P}. \end{align} $$
By the previous claim, the disintegration (see, e.g., [Reference Ambrosio, Gigli and Savaré3, Theorem 5.3.1] for details on the disintegration theorem) of the common measure
$\boldsymbol {\mu }:= (X, {\boldsymbol {L}} X)_{\sharp}\mathbb {P} $
with respect to its first marginal
$\mu $
is given by
$\delta _{\boldsymbol {f}_X(\cdot )}$
which should coincide with
$\delta _{\boldsymbol {f}_X'(\cdot )}\ \mu $
-a.e. in
$\mathsf {X}$
. Since
$\boldsymbol {f}_X$
and
$\boldsymbol {f}_{X'}$
are both Lipschitz continuous and coincide
$\mu $
-a.e., they coincide on
$\operatorname {\mathrm {supp}}(\mu )$
.
(d) The map
${\boldsymbol {f}}_{{\boldsymbol {L}}}$
is continuous on
$\mathcal {S}(\mathsf {X})$
.
Let us consider a sequence
$(x_n,\mu _n)_n$
in
$\mathcal {S}(\mathsf {X})$
converging to
$(x,\mu )\in \mathcal {S}(\mathsf {X})$
, and let us prove that there exists an increasing subsequence
$k\mapsto n(k)$
such that
${\boldsymbol {f}}_{{\boldsymbol {L}}}(x_{n(k)},\mu _{n(k)})\to {\boldsymbol {f}}_{{\boldsymbol {L}}}(x,\mu )$
as
$k\to \infty $
.
By Proposition 3.18, we can find a limit map
$X\in \mathcal {X}$
and a sequence
$X_n\in \mathcal {X}$
converging to X such that
$(X_n)_{\sharp}\mathbb {P}=\mu _n,\ X_{\sharp}\mathbb {P}=\mu $
. Since
${\boldsymbol {L}} X_n\to {\boldsymbol {L}} X$
, we can then extract a subsequence
$k\mapsto n(k)$
and find a set of full measure
$\Omega _{0}\subset \Omega $
such that
$X_{n(k)}(\omega )\to X(\omega )$
and
$Y_{n(k)}(\omega )\to Y(\omega )$
as
$k\to \infty $
for every
$\omega \in \Omega _{0}$
, where
$Y_n:={\boldsymbol {L}} X_n,\ Y:={\boldsymbol {L}} X$
.
Let us fix
$\varepsilon>0$
; since
$x\in \operatorname {\mathrm {supp}}(\mu )$
and
$X(\Omega _{0})\cap \operatorname {\mathrm {supp}}(\mu )$
is dense in
$\operatorname {\mathrm {supp}}(\mu )$
, we can find
$\omega \in \Omega _{0}$
such that
$|X(\omega )-x|_{\mathsf {X}}\le \varepsilon $
. We then obtain
$$ \begin{align*} |{\boldsymbol{f}}_{{\boldsymbol{L}}}(x_{n(k)},\mu_{n(k)})-{\boldsymbol{f}}_{{\boldsymbol{L}}}(x,\mu)|_{\mathsf{Y}} &\le |{\boldsymbol{f}}_{{\boldsymbol{L}}}(x_{n(k)},\mu_{n(k)})- {\boldsymbol{f}}_{{\boldsymbol{L}}}(X_{n(k)}(\omega),\mu_{n(k)})|_{\mathsf{Y}} \\&\quad + |{\boldsymbol{f}}_{{\boldsymbol{L}}}(X_{n(k)}(\omega),\mu_{n(k)})- {\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),\mu)|_{\mathsf{Y}} \\&\quad+ |{\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),\mu)-{\boldsymbol{f}}_{{\boldsymbol{L}}}(x,\mu)|_{\mathsf{Y}} \\&\le L| x_{n(k)}-X_{n(k)}(\omega)|_{\mathsf{X}}+|Y_{n(k)}(\omega)-Y(\omega)|_{\mathsf{Y}}\\ &\quad+ L|X(\omega)-x|_{\mathsf{X}}. \end{align*} $$
Taking the
$\limsup $
as
$k\to \infty $
, we get
$$\begin{align*}\limsup_{k\to\infty} |{\boldsymbol{f}}_{{\boldsymbol{L}}}(x_{n(k)},\mu_{n(k)})-{\boldsymbol{f}}_{{\boldsymbol{L}}}(x,\mu)|_{\mathsf{Y}} \le 2 L\varepsilon, \end{align*}$$
and, since
$\varepsilon>0$
is arbitrary, we obtain the convergence.
We prove item (2): by Theorem 4.5, it is enough to prove the statement in case the map
${\boldsymbol {L}}$
is defined on the whole
$\mathcal {X}$
. We can then apply the previous claim with
$\mathsf {Y}=\mathsf {X}$
and
$p=q=2.$
In the particular case, when
$p=q=2$
and
$\mathsf {X}=\mathsf {Y}$
is a Hilbert space, also
$\lambda $
-dissipativity (2.23) is inherited from
${\boldsymbol {L}}$
to its representative map
${\boldsymbol {f}}_{{\boldsymbol {L}}}$
.
Proposition 4.8 (
$\lambda $
-dissipative representations)
Let us suppose that
$p=2$
,
$\mathsf {X}$
is a separable Hilbert space, and
${\boldsymbol {L}}:\mathcal {X}\to \mathcal {X}$
is an invariant Lipschitz
$\lambda $
-dissipative operator. Then, for every
$\mu \in \mathcal {P}_{2}(\mathsf {X})$
, the map
${\boldsymbol {f}}_{{\boldsymbol {L}}}(\cdot ,\mu )$
of Theorem 4.7 is (pointwise)
$\lambda $
-dissipative, i.e.,
$$ \begin{align} \langle {\boldsymbol{f}}_{{\boldsymbol{L}}}(x,\mu)-{\boldsymbol{f}}_{{\boldsymbol{L}}}(x',\mu),x-x'\rangle_{\mathsf{X}}\le \lambda |x-x'|^{2} \quad\text{for every }x,x'\in \operatorname{\mathrm{supp}}(\mu). \end{align} $$
Remark 4.9 Recalling Remark 2.6,
${\boldsymbol {L}}:\mathcal {X}\to \mathcal {X}$
is an invariant Lipschitz
$\lambda $
-dissipative operator if and only if its
$\lambda $
-transformation
${\boldsymbol {L}}^\lambda :={\boldsymbol {L}}-\lambda \boldsymbol {i}_{\mathcal {X}}$
is an invariant Lipschitz dissipative operator. Moreover, by applying Theorem 4.7 to both
${\boldsymbol {L}}$
and
${\boldsymbol {L}}^\lambda $
, we can identify
$$\begin{align*}{\boldsymbol{f}}_{{\boldsymbol{L}}^\lambda}(x,\mu)\equiv {\boldsymbol{f}}_{{\boldsymbol{L}}}(x,\mu)-\lambda x,\quad\text{for every }(x,\mu)\in\mathcal{S}(\mathsf{X}),\end{align*}$$
so that both
${\boldsymbol {f}}_{{\boldsymbol {L}}}$
and
${\boldsymbol {f}}_{{\boldsymbol {L}}^\lambda }$
satisfy (4.10) with
${\boldsymbol {L}}$
and
${\boldsymbol {L}}^\lambda $
, respectively.
Proof Thanks to Remark 4.9, proving the
$\lambda $
-dissipativity in (4.13) for
${\boldsymbol {L}}$
is equivalent to prove the
$0$
-dissipativity result in (4.13) for
${\boldsymbol {L}}^\lambda $
.
We keep the same notation of the proof of Theorem 4.7 applied to
${\boldsymbol {L}}^\lambda $
. The case when
$\mu =X_{\sharp}\mathbb {P}$
, with
$X\in \mathcal {X}_m$
for some
$m\in \mathbb {N}$
, follows as in claim (a) of the proof of Theorem 4.7: we can assume that
${\boldsymbol {L}}^\lambda X$
is constant on every
$\Omega _{m,k}$
. If
$\omega ',\omega "\in \Omega $
and
$\omega '\in \Omega _{m,i}$
,
$\omega " \in \Omega _{m,j}$
,
$i,j\in I_m$
and
$g\in \mathrm {S}(\Omega )$
is a measure-preserving isomorphism induced by the permutation that swaps i and j as in Corollary 3.7, we get
$$\begin{align*}\frac 1{2^{m-1}}\langle {\boldsymbol{L}}^\lambda X(\omega')-{\boldsymbol{L}}^\lambda X(\omega"),X(\omega')-X(\omega")\rangle_{\mathsf{X}} \le 0. \end{align*}$$
We can eventually argue by approximation, as in claim (b) of the proof of Theorem 4.7, and using the representation of
${\boldsymbol {L}}^\lambda X$
in terms of
${\boldsymbol {f}}_{{\boldsymbol {L}}^\lambda }$
to get
$$ \begin{align} \langle {\boldsymbol{f}}_{{\boldsymbol{L}}^\lambda}(x,\mu)-{\boldsymbol{f}}_{{\boldsymbol{L}}^\lambda}(x',\mu),x-x'\rangle_{\mathsf{X}}\le 0 \quad\text{for every }x,x'\in \operatorname{\mathrm{supp}}(\mu).\\[-32pt]\nonumber \end{align} $$
Proposition 4.10 (Stability of Lipschitz representations)
If
${\boldsymbol {L}}_n, {\boldsymbol {L}}:\mathcal {X}\to \mathcal {Y}$
are L-Lipschitz invariant maps and
$D\subset \mathcal {X}$
is an invariant closed set, such that
$$ \begin{align} {\boldsymbol{L}}_n X\to {\boldsymbol{L}} X\quad\text{for every }X\in D, \end{align} $$
then setting
$\tilde D:=\big \{X_{\sharp}\mathbb {P}:X\in D\big \}$
, we have
${\boldsymbol {f}}_{{\boldsymbol {L}}_n}\to {\boldsymbol {f}}_{{\boldsymbol {L}}}$
pointwise in
$\mathcal {S}(\mathsf {X},\tilde D)$
, where
${\boldsymbol {f}}_{{\boldsymbol {L}}}$
is as in Theorem 4.7.
Proof We fix
$\mu \in \tilde D$
and we set
$\boldsymbol {f}_n:={\boldsymbol {f}}_{{\boldsymbol {L}}_n}(\cdot ,\mu ):\operatorname {\mathrm {supp}}(\mu )\to \mathsf {Y}$
. We observe that
$\boldsymbol {f}_n$
are L-Lipschitz and form a Cauchy sequence in
$L^q(\mathsf {X},\mu ;\mathsf {Y})$
: we denote by
$\tilde {\boldsymbol {f}}$
its limit. For every
$x\in \operatorname {\mathrm {supp}}(\mu )$
and
$\rho>0$
, we can set
$$ \begin{align} \boldsymbol{f}_{n,\rho}(x):=\frac1{\mu(B(x,\rho))}\int_{B(x,\rho)}\boldsymbol{f}_n(u)\,\mathrm{d}\mu(u),\quad \boldsymbol{f}_{\rho}(x):=\frac1{\mu(B(x,\rho))}\int_{B(x,\rho)}\tilde {\boldsymbol{f}}(u)\,\mathrm{d}\mu(u). \end{align} $$
We have
$\boldsymbol {f}_{n,\rho }(x)\to \boldsymbol {f}_\rho (x)$
for every
$x\in \operatorname {\mathrm {supp}}(\mu )$
and every
$\rho>0$
. On the other hand,
$$\begin{align*}|\boldsymbol{f}_{n,\rho}(x)-\boldsymbol{f}_n(x)|_{\mathsf{Y}}\le L\rho,\end{align*}$$
so that a simple argument using the triangle inequality shows that the sequence
$(\boldsymbol {f}_n(x))_{n\in \mathbb {N}}$
is Cauchy in
$\mathsf {Y}$
for every
$x\in \operatorname {\mathrm {supp}}(\mu )$
and its pointwise limit
$\boldsymbol {g}(\cdot ,\mu )$
is L-Lipschitz and represents
${\boldsymbol {L}}$
as in (4.10) for every
$X \in D$
. Arguing as in claim (d) in the proof of Theorem 4.7 and using the continuity of
${\boldsymbol {L}}$
, we can eventually deduce that
$\boldsymbol {g}$
is continuous in
$\mathcal {S}(\mathsf {X},\tilde D)$
. The fact that
$\boldsymbol {g}={\boldsymbol {f}}_{{\boldsymbol {L}}}$
comes from Lemma 4.6.
When the maps
${\boldsymbol {L}}_n$
are not uniformly Lipschitz, we can still obtain a limiting representation.
Lemma 4.11 Let
$D \subset \mathcal {X}$
and
${\boldsymbol {L}}_n, {\boldsymbol {L}}: D \to \mathcal {Y}$
be maps such that
${\boldsymbol {L}}_n$
are law invariant,
${\boldsymbol {L}}_n$
converge pointwise to
${\boldsymbol {L}}$
on D as
$n\to \infty $
and there exist Borel functions
$\boldsymbol {f}_n: \mathcal {S}(\mathsf {X}, \iota (D)) \to \mathsf {Y}$
such that
$$\begin{align*}\text{for every}\ n \in \mathbb{N}\ \text{and every}\ X\in D,\quad {\boldsymbol{L}}_n X(\omega)=\boldsymbol{f}_n(X(\omega),X_{\sharp}\mathbb{P})\ \text{for a.e}.~\omega\in \Omega. \end{align*}$$
Then
${\boldsymbol {L}}$
is law invariant and, for every
$\mu \in \iota (D)$
, there exists a map
$\boldsymbol {f}[\mu ] \in L^q(\mathsf {X}, \mu; \mathsf {Y})$
such that, for every
$X \in D$
, there exists an increasing subsequence
$k \mapsto n_{k}$
such that
$$\begin{align*}\lim_{k} \boldsymbol{f}_{n_{k}}(X(\omega), X_{\sharp}\mathbb{P}) = \boldsymbol{f}[X_{\sharp}\mathbb{P}](X(\omega)) = {\boldsymbol{L}} X (\omega) \text{ for a.e.~} \omega\in \Omega.\end{align*}$$
Proof First of all, notice that
${\boldsymbol {L}}$
is law invariant, being pointwise limit of law invariant maps. Let
$\mu \in \iota (D)$
be fixed. If
$X\in D$
is such that
$X_{\sharp}\mathbb {P}=\mu $
, we can find an increasing subsequence
$k \mapsto n_{k}$
such that
${\boldsymbol {L}}_{n_{k}} X \to {\boldsymbol {L}} X\ \mathbb {P}$
-a.e. in
$\Omega $
and define
$$\begin{align*}\boldsymbol{f}_X(x):= \begin{cases} \lim_{k \to + \infty}\boldsymbol{f}_{n_{k}}(x, \mu), \quad &\text{ if } x \in E, \\ 0, \quad &\text{ else}, \end{cases}\end{align*}$$
where
$E \subset \mathsf {X}$
is the Borel set of points in
$\mathsf {X}$
where
$\lim _{k \to + \infty }\boldsymbol {f}_{n_{k}}(x, \mu )$
exists. Let us now show that
$\boldsymbol {f}_X$
represents
${\boldsymbol {L}}$
, i.e.,
$$\begin{align*}{\boldsymbol{L}} X(\omega)=\boldsymbol{f}_X (X(\omega))\ \text{for a.e}.~\omega\in \Omega. \end{align*}$$
We know that
$$\begin{align*}\text{for every}\ k \in \mathbb{N} \quad {\boldsymbol{L}}_{n_{k}} X(\omega)=\boldsymbol{f}_{n_{k}}(X(\omega),X_{\sharp}\mathbb{P})\ \text{for a.e}.~ \omega\in \Omega, \end{align*}$$
so that, choosing representatives of X,
${\boldsymbol {L}} X$
,
${\boldsymbol {L}}_{n_{k}}X$
, we can find a full
$\mathbb {P}$
-measure set
$\Omega _{0} \subset \Omega $
such that
$$\begin{align*}{\boldsymbol{L}} X(\omega) = \lim_{k \to + \infty} {\boldsymbol{L}}_{n_{k}}X (\omega) = \lim_{k \to +\infty} \boldsymbol{f}_{n_{k}}(X(\omega), X_{\sharp}\mathbb{P}) \quad \text{ for every }\omega \in \Omega_{0}. \end{align*}$$
Thus, for every
$\omega \in \Omega _{0}$
,
$X(\omega ) \in E$
and then
${\boldsymbol {L}} X(\omega ) = f_X(X(\omega ))$
. If now
$X' \in D$
is such that
${X'}_{\sharp}\mathbb {P}=\mu $
, arguing as in claim (c) of the proof of Theorem 4.7, it is easy to see that
$\boldsymbol {f}_X=\boldsymbol {f}_{X'}\ \mu $
-almost everywhere.
We eventually apply the previous results to (possibly multivalued) maximal
$\lambda $
-dissipative operators
$\boldsymbol {B}\subset \mathcal {X}\times \mathcal {X}$
(with
$p=q=2$
and
$\mathsf {X}=\mathsf {Y}$
) which are invariant by measure-preserving isomorphisms. We show that the invariance property is inherited by the associated resolvent operator, Yosida approximation, minimal selection, and semigroup which also enjoy a map-representation property.
We denote by
$\iota \big (D(\boldsymbol {B})\big ):=\Big \{X_{\sharp}\mathbb {P}:X\in \mathrm {D}(\boldsymbol {B})\Big \}$
the image in
$\mathcal {P}_{2}(\mathsf {X})$
of the domain of
$\boldsymbol {B}$
.
Theorem 4.12 (Structure of resolvents, Yosida approximations, and semigroups)
Let
$\mathsf {X}$
be a separable Hilbert space, and let
$p=2$
. Let
$\boldsymbol {B} \subset \mathcal {X} \times \mathcal {X}$
be a maximal
$\lambda $
-dissipative operator which is invariant by measure-preserving isomorphisms. Then, for every
$0<\tau <1/\lambda ^+,\ t\ge 0$
, the operators
$ \boldsymbol {B}, \boldsymbol {B}_{\tau }, {\boldsymbol {J}_{\tau }},\boldsymbol {S}_t,\boldsymbol {B}^\circ $
are law invariant. Moreover, there exist (uniquely defined) continuous maps
$\boldsymbol {j}_{\tau }:\mathcal {S}(\mathsf {X})\to \mathsf {X}$
,
$\boldsymbol {b}_{\tau }: \mathcal {S}(\mathsf {X}) \to \mathsf {X}$
, and
$ \boldsymbol {s}_t:\mathcal {S}(\mathsf {X},\overline {\iota \big (D(\boldsymbol {B})\big )})\to \mathsf {X}$
such that:
-
(1) for every
$\mu \in \mathcal {P}_{2}(\mathsf {X})$
, the map
$\boldsymbol {j}_{\tau }(\cdot ,\mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is
$(1-\lambda \tau )^{-1}$
-Lipschitz continuous, for
$0<\tau < 1/\lambda ^+$
, -
(2) for every
$\mu \in \mathcal {P}_{2}(\mathsf {X})$
, the map
$\boldsymbol {b}_{\tau }(\cdot ,\mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is
$\frac {2-\lambda \tau }{\tau (1-\lambda \tau )}$
-Lipschitz continuous, for
$0<\tau < 1/\lambda ^+$
, -
(3) for every
$\mu \in \overline {\iota \big (D(\boldsymbol {B})\big )}$
, the map
$\boldsymbol {s}_t(\cdot ,\mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is
$e^{\lambda t}$
-Lipschitz continuous,
and
$$ \begin{align} \text{ for every}\ X \in \mathcal{X}, {\boldsymbol{J}_{\tau}} X(\omega)=\boldsymbol{j}_{\tau}(X(\omega),X_{\sharp}\mathbb{P}) \text{for}\ \mathbb{P}-\text{a.e}.~\omega \in \Omega, \end{align} $$
$$ \begin{align} \text{ for every}\ X \in \mathcal{X}, \boldsymbol{B}_{\tau} X(\omega)=\boldsymbol{b}_{\tau}(X(\omega),X_{\sharp}\mathbb{P}) \text{ for}\ \mathbb{P}-\text{a.e}.~\omega \in \Omega, \end{align} $$
$$ \begin{align} \text{ for every}\ X \in \overline{\mathrm{D}(\boldsymbol{B})}, \boldsymbol{S}_t X(\omega)=\boldsymbol{s}_t(X(\omega),X_{\sharp}\mathbb{P}) \text{ for}\ \mathbb{P}-\text{a.e}.~\omega \in \Omega, \end{align} $$
together with the invariance and semigroup properties
$$ \begin{align} \begin{aligned} \mu\in \overline{\iota\big(D(\boldsymbol{B})\big)}&\quad\Rightarrow\quad \boldsymbol{s}_t(\cdot,\mu)_\sharp\mu\in \overline{\iota\big(D(\boldsymbol{B})\big)};\\ \mu\in {\iota\big(D(\boldsymbol{B})\big)}&\quad\Rightarrow\quad \boldsymbol{s}_t(\cdot,\mu)_\sharp\mu\in {\iota\big(D(\boldsymbol{B})\big)},\\ \boldsymbol{s}_{t+h}(x,\mu)=\boldsymbol{s}_h(\boldsymbol{s}_t(x,\mu),\boldsymbol{s}_t(\cdot,\mu)_\sharp\mu)&\quad \text{for every }(x,\mu) \in \mathcal{S}(\mathsf{X},\overline{\iota\big(D(\boldsymbol{B})\big)}),\quad t,h\ge0. \end{aligned} \end{align} $$
Finally, for every
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, there exists a map
$\boldsymbol {b}^\circ (\cdot ,\mu ) \in L^{2}(\mathsf {X}, \mu; \mathsf {X})$
such that for every
$X\in \mathcal {X}$
,
$$ \begin{align} \text{ if}\ X_{\sharp}\mathbb{P}=\mu, \text{then}\ X \in \mathrm{D}(\boldsymbol{B}), \boldsymbol{B}^\circ X(\omega)=\boldsymbol{b}^\circ(X(\omega),\mu) \text{for}\ \mathbb{P}-\text{a.e}.~\omega \in \Omega. \end{align} $$
For every
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, the map
$\boldsymbol {b}^\circ (\cdot ,\mu )$
is
$\lambda $
-dissipative in a set
$\mathsf {X}_{0}\subset \mathsf {X}$
of full
$\mu $
-measure and satisfies
$$ \begin{align} \lim_{h\downarrow0}\int\bigg|\frac 1h(\boldsymbol{s}_{t+h}(x,\mu)-\boldsymbol{s}_t(x,\mu))- \boldsymbol{b}^\circ(\boldsymbol{s}_t(x,\mu),\boldsymbol{s}_t(\cdot,\mu)_\sharp \mu)\bigg|^{2}\,\mathrm{d}\mu(x)=0\quad t\ge0. \end{align} $$
Remark 4.13 By Theorem 4.12, a maximal
$\lambda $
-dissipative operator
$\boldsymbol {B} \subset \mathcal {X} \times \mathcal {X}$
,
$\lambda \in \mathbb {R}$
, is law invariant if and only if it is invariant by measure-preserving isomorphisms. Thanks to (4.21), also
$D(\boldsymbol {B})$
is law invariant, i.e., if
$X\in D(\boldsymbol {B})$
and
$Y\in \mathcal {X}$
is such that
$Y_{\sharp}\mathbb {P}=X_{\sharp}\mathbb {P}$
, then
$Y\in D(\boldsymbol {B})$
.
Proof First, notice that
$\boldsymbol {B}$
is closed being maximal
$\lambda $
-dissipative; hence, it is law invariant by Proposition 4.2. Recall that
${\boldsymbol {J}_{\tau }}$
is everywhere defined,
$(1-\lambda \tau )^{-1}$
-Lipschitz continuous for every
$0<\tau <1/\lambda ^+$
(see Section 2.3) and invariant by measure-preserving isomorphisms by Proposition 2.9. Fixed
$0<\tau <1/\lambda ^+$
, we can thus apply Proposition 4.2 and Theorem 4.7(1) and get that
${\boldsymbol {J}_{\tau }}$
is law invariant together with property (1) in Theorem 4.12 and (4.17). Similarly,
$\boldsymbol {S}_t$
is defined on the closed set
$\overline {\mathrm {D}(\boldsymbol {B})}$
, and it is
$e^{\lambda t}$
-Lipschitz continuous (cf. Section 2.3) and invariant by measure-preserving isomorphisms by Proposition 2.9, so that we can apply Proposition 4.2 and Theorem 4.7(1) and get that it is law invariant together with property (3) of Theorem 4.12 and (4.19). The content of (4.20) immediately follows by the semigroup and invariance properties of
$\boldsymbol {S}_t$
(cf. Section 2.3), also using that
$\overline {\iota (\mathrm {D}(\boldsymbol {B}))}=\iota (\overline {\mathrm {D}(\boldsymbol {B})})$
.
We now prove (4.21). If
$X \in \mathrm {D}(\boldsymbol {B})$
, we have that
$\boldsymbol {B}_{\tau } X \to \boldsymbol {B}^\circ X$
as
$\tau \downarrow 0$
; moreover,
$\boldsymbol {B}_{\tau }$
is law invariant, everywhere defined and, for every
$0<\tau < 1/\lambda ^+$
,
$\boldsymbol {B}_{\tau }$
is
$\lambda /(1-\lambda \tau )$
-dissipative and
$\frac {2-\lambda \tau }{\tau (1-\lambda \tau )}$
-Lipschitz continuous (cf. Section 2.3). Hence, we can apply Theorem 4.7(2) and get that
$\boldsymbol {B}^\circ $
is law invariant and that there exists, for every
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, a map
$\boldsymbol {b}^\circ [\mu ]\equiv \boldsymbol {b}^\circ (\cdot ,\mu )\in L^{2}(\mathsf {X},\mu; \mathsf {X})$
such that for every
$X \in \mathrm {D}(\boldsymbol {B}),$
$$ \begin{align} \boldsymbol{B}^\circ X (\omega) = &\boldsymbol{b}^\circ[\mu](X(\omega)) \text{ for}\ \mathbb{P}-\text{a.e}.~\omega \in \Omega, \end{align} $$
$$ \begin{align} \text{there exists}\ \tau_{k} \downarrow 0\ \text{s.t. } &\boldsymbol{b}_{\tau_{k}}(X(\omega), \mu) \to \boldsymbol{b}^{\circ}[\mu](X(\omega)) \text{ for}\ \mathbb{P}-\text{a.e}.~\omega \in \Omega, \end{align} $$
where
$\boldsymbol {b}_{\tau }$
is the (unique) continuous map that represents
$\boldsymbol {B}_{\tau }$
coming from Theorem 4.7(1),
$0<\tau < 1/\lambda ^+$
. To complete the proof of (4.21), we have to check that, if
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
and
$X\in \mathcal {X}$
is such that
$X_{\sharp}\mathbb {P}=\mu $
, then
$X\in \mathrm {D}(\boldsymbol {B})$
. Since
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, there exists
$Y\in \mathrm {D}(\boldsymbol {B})$
such that
$Y_{\sharp}\mathbb {P}=X_{\sharp}\mathbb {P}=\mu $
. By (4.18), we have
$$ \begin{align*} |\boldsymbol{B}_{\tau} Y|^{2}_{\mathcal{X}}&=\int |b_{\tau}(Y(\omega),\mu)|^{2}\mathrm{d}\mathbb{P}(\omega)=\int |b_{\tau}(x,\mu)|^{2}\mathrm{d}\mu(x)\\ &=\int |b_{\tau}(X(\omega),\mu)|^{2}\mathrm{d}\mathbb{P}(\omega)=|\boldsymbol{B}_{\tau} X|_{\mathcal{X}}^{2}. \end{align*} $$
Hence, since
$Y\in \mathrm {D}(\boldsymbol {B})$
, by (2.24), we have
$$\begin{align*}(1-\lambda\tau)|\boldsymbol{B}_{\tau} X|_{\mathcal{X}}=(1-\lambda\tau)|\boldsymbol{B}_{\tau} Y|_{\mathcal{X}}\uparrow |\boldsymbol{B}^\circ Y|_{\mathcal{X}}<+\infty,\quad\text{as }\tau\downarrow 0.\end{align*}$$
Recalling (2.25), we get
$X\in \mathrm {D}(\boldsymbol {B})$
. Finally, (4.22) follows by (2.27) using (4.19) and (4.21).
It only remains to show that, for every
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, the map
$\boldsymbol {b}^\circ [\mu ]$
is
$\lambda $
-dissipative in a full
$\mu $
-measure set. To this aim, observe that we can apply Theorem 4.7(1) to
$\boldsymbol {B}_{\tau }$
,
$0<\tau <1/\lambda ^+$
, so that for every
$\mu \in \mathcal {P}_{2}(\mathsf {X})$
, we have
$$ \begin{align} \langle \boldsymbol{b}_{\tau}(y)-\boldsymbol{b}_{\tau}(y'), y-y' \rangle \le \frac{\lambda}{1-\lambda\tau} |y-y'|^{2} \quad \text{ for every } y,y' \in \operatorname{\mathrm{supp}}(\mu). \end{align} $$
Let
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, and let us consider a representative of
$X \in \mathrm {D}(\boldsymbol {B})$
such that
$X_{\sharp}\mathbb {P}=\mu $
; let
$\tau _{k}$
be a sequence as in (4.24) and let
$\Omega _{0}$
be a full
$\mathbb {P}$
-measure set where the convergence in (4.24) takes place. If we take
$y,y' \in X(\Omega _{0}) \cap \operatorname {\mathrm {supp}}(\mu )$
, then we can find
$\omega , \omega ' \in \Omega _{0}$
such that
$X(\omega )=y$
and
$X(\omega ')=y'$
so that, passing to the limit as
$k \to + \infty $
in (4.25) written for
$\tau =\tau _{k}$
, we get that
$$\begin{align*}\langle \boldsymbol{b}^{\circ}[\mu](y)-\boldsymbol{b}^\circ[\mu](y'), y-y' \rangle \le \lambda |y-y'|^{2} \quad \text{ for every } y,y' \in X(\Omega_{0}) \cap \operatorname{\mathrm{supp}}(\mu). \end{align*}$$
It is then enough to observe that
$X(\Omega _{0}) \cap \operatorname {\mathrm {supp}}(\mu )$
contains a Borel set
$\mathsf {X}_{0}$
of full
$\mu $
-measure to conclude: in fact, being
$X(\Omega _{0})$
a Suslin set, we can find two Borel sets
$E_{0}, E_1$
such that
$E_{0} \subset X(\Omega _{0}) \subset E_1$
and
$\mu (E_1 \setminus E_{0})=0$
. Since
$\mu (E_1)=X_{\sharp}\mathbb {P} (E_1) \ge \mathbb {P}(\Omega _{0})=1$
, we conclude that we can take
$\mathsf {X}_{0}:=E_{0} \cap \operatorname {\mathrm {supp}}(\mu )$
.
A An alternative proof of the extension theorem for
$\textsf {G}$
-invariant Lipschitz maps
We provide an alternative proof to the extension result for invariant Lipschitz maps stated in Theorem 2.11. Here, we use a recent and beautiful explicit construction of a Lipschitz extension provided by [Reference Azagra, Le Gruyer and Mudarra5] (see also [Reference Azagra, Le Gruyer and Mudarra4]) and we show that it preserves the invariance. We consider a Hilbert space
$\mathcal {H}$
with norm
$|\cdot |$
and scalar product
$\langle \cdot , \cdot \rangle $
as in Section 2.4.
Recall that if
$g:\mathsf {W}\to \mathbb {R}$
is a function defined in a Hilbert space
$\mathsf {W}$
, then its convex envelope is defined by
$$ \begin{align} \operatorname{co}(g)(w):= \inf\left\{\sum_{i=1}^N \alpha_i g(w_i): \alpha_i\ge0,\ \sum_{i=1}^N\alpha_i=1,\ w_i\in \mathsf{W},\ \sum_{i=1}^N \alpha_i w_i=w,\ N\in \mathbb{N}\right\}. \end{align} $$
If g is locally bounded from above, then also
$\operatorname {co}(g)$
is locally bounded from above and it is therefore locally Lipschitz.
Theorem A.1 [Reference Azagra, Le Gruyer and Mudarra5]
Let
$f:D\to \mathcal {H}$
be an L-Lipschitz map defined in
$D\subset \mathcal {H}$
. Setting for every
$x,y\in \mathcal {H}$
$$ \begin{align} \begin{aligned} g(x,y):={}& \inf_{x'\in D} \Big\{\langle f(x'),y\rangle+ \frac L2 |(x-x',y)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(x,y)|_{\mathcal{H}\times \mathcal{H}}^{2},\\ \tilde g:={}&\operatorname{co}(g), \end{aligned} \end{align} $$
then
$\tilde g$
is a convex function of class
$\mathrm {C}^{1,1}$
in
$\mathcal {H}\times \mathcal {H}$
and its partial differential with respect to the second variable in
$\mathcal {H}$
$$ \begin{align} F(x):=\nabla_y \tilde g(x,0), \quad x \in \mathcal{H}, \end{align} $$
is an L-Lipschitz extension of f.
We state our first result concerning the extension of
$\mathsf {G}_{\mathcal {H}}$
-invariant Lipschitz maps.
Theorem A.2 Under the same assumption of Theorem A.1, let us also suppose that f is
$\mathsf {G}_{\mathcal {H}}$
-invariant according to (2.29). Then F is
$\mathsf {G}_{\mathcal {H}}$
-invariant as well. In particular, any
$\mathsf {G}_{\mathcal {H}}$
-invariant L-Lipschitz function
$f:D\to \mathcal {H}$
defined in a subset D of
$\mathcal {H}$
admits a
$\mathsf {G}_{\mathcal {H}}$
-invariant L-Lipschitz extension
$F:\mathcal {H}\to \mathcal {H}.$
Proof We divide the proof in several claims.
Claim 1: the map g is
$\mathsf {G}_{\mathcal {H}}$
-invariant, i.e.,
$g(Ux,Uy)=g(x,y)$
for every
$(x,y)\in \mathcal {H}\times \mathcal {H}$
and
$U\in \mathsf {G}_{\mathcal {H}}.$
Every element
$x'\in D$
can be written as
$x'=Ux"$
with
$x"=U^{-1}x'\in D$
, so that for every
$U\in \mathsf {G}_{\mathcal {H}}$
and
$(x,y)\in \mathcal {H}\times \mathcal {H}$
,
$$ \begin{align*} g(Ux,Uy)&= \inf_{x'\in D} \Big\{\langle f(x'),Uy\rangle+ \frac L2 |(Ux-x',Uy)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(Ux,Uy)|_{\mathcal{H}\times \mathcal{H}}^{2} \\&= \inf_{x"\in D} \Big\{\langle f(Ux"),Uy\rangle+ \frac L2 |(U(x-x"),Uy)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(Ux,Uy)|_{\mathcal{H}\times \mathcal{H}}^{2} \\&= \inf_{x"\in D} \Big\{\langle f(x"),y\rangle+ \frac L2 |(x-x",y)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(x,y)|_{\mathcal{H}\times \mathcal{H}}^{2} \\&=g(x,y), \end{align*} $$
where we used (2.29) and the isometric character of U to get
$\langle f(Ux"),Uy\rangle = \langle Uf(x"),Uy\rangle = \langle f(x"),y\rangle $
.
Claim 2: the map
$\tilde g:=\operatorname {co}(g)$
is
$\mathsf {G}_{\mathcal {H}}$
-invariant as well.
It is sufficient to observe that for every
$U\in \mathsf {G}_{\mathcal {H}},\ N\in \mathbb {N}$
, and
$\alpha _i\ge 0$
with
$\sum _{i=1}^N\alpha _i=1$
, a collection
$\{(x_i,y_i)\}_{i=1}^N \in (\mathcal {H}\times \mathcal {H})^N$
satisfies
$\sum _{i=1}^N \alpha _i (x_i,y_i)=(x,y)$
if and only if
$\sum _{i=1}^N \alpha _i (U x_i,Uy_i)=(Ux,Uy)$
. Using (A.1) and the invariance of g, we thus obtain
$\tilde g(Ux,Uy)=\tilde g(x,y)$
for every
$x,y \in \mathcal {H}$
.
Claim 3: the map
$F:=\nabla _y \tilde {g}(\cdot ,0)$
is
$\mathsf {G}_{\mathcal {H}}$
-invariant.
Since we know that
$\tilde g$
is Frechét differentiable, we observe that
$z= F(x)$
if and only if
$$\begin{align*}\tilde g(x,y)= \tilde g(x,0)+\langle z,y\rangle +o(|y|)\quad \text{as }y\to 0. \end{align*}$$
Being
$\tilde g$
invariant, for every
$U\in \mathsf {G}_{\mathcal {H}}$
and
$x\in \mathcal {H}$
, the above formula immediately yields
$$ \begin{align*} \tilde g(Ux,y)&= \tilde g(Ux,UU^{-1}y)= \tilde g(x,U^{-1}y) \\&= \tilde g(x,0)+\langle z,U^{-1}y\rangle +o(|U^{-1}y|) \\&= \tilde g(Ux,0)+\langle Uz,y\rangle +o(|y|) \quad \text{as }y\to 0, \end{align*} $$
so that
$F(Ux)=Uz=UF(x)$
.
Open access
