Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-20T06:25:35.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Extreme Version of Projectivity for Normed Modules Over Sequence Algebras

Published online by Cambridge University Press:  20 November 2018

A. Ya. Helemskii
A. Ya. Helemskii*
Affiliation:
Faculty of Mechanics and Mathematics, Moscow State University, Moscow 119992 , Russia, e-mail: helemskii@rambler.ru
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define and study the so-called extreme version of the notion of a projective normed module. The relevant definition takes into account the exact value of the norm of the module in question, in contrast with the standard known definition that is formulated in terms of norm topology.

After the discussion of the case where our normed algebra 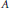$A$ is just 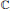$\mathbb{C}$, we concentrate on the case of the next degree of complication, where 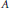$A$ is a sequence algebra satisfying some natural conditions. The main results give a full characterization of extremely projective objects within the subcategory of the category of non-degenerate normed 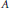$A$-modules, consisting of the so-called homogeneous modules. We consider two cases, ‘non-complete’ and ‘complete’, and the respective answers turn out to be essentially different.

In particular, all Banach non-degenerate homogeneous modules consisting of sequences are extremely projective within the category of Banach non-degenerate homogeneous modules. However, neither of them, provided it is infinite-dimensional, is extremely projective within the category of all normed non-degenerate homogeneous modules. On the other hand, submodules of these modules consisting of finite sequences are extremely projective within the latter category.

Keywords

46H25extremely projective modulesequence algebrahomogeneous module
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 3 , 01 June 2013 , pp. 559 - 574
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Blecher, D. P., The standard dual of an operator space. Pacific J. Math. 153(1992), 15–30.Google Scholar
[2] Cigler, J., Losert, V. and Michor, P., Banach modules and functors on categories of Banach spaces. Marcel Dekker, New York, 1979.Google Scholar
[3] Effros, E. G. and Ruan, Z.-J., Operator spaces. Clarendon Press. Oxford. 2000.Google Scholar
[4] Grothendieck, A., Une caracterisation vectorielle-metrique des espaces L1. Canad. J. Math. 7(1955), 552–561. http://dx.doi.org/10.4153/CJM-1955-060-6 Google Scholar
[5] Helemskii, A. Ya., On the homological dimensions of normed modules over Banach algebras. (Russian) Mat. Sb. (N.S.) 81(1970), 430–444; Math. USSR Sb. 10(1970), 399–411.Google Scholar
[6] Helemskii, A. Ya., A certain class of flat Banach modules and its applications. (Russian) Vestnik Moskov. Univ. Ser. Mat. Meh. 27(1972), 29–36.Google Scholar
[7] Helemskii, A. Ya., The Homology of Banach and Topological Algebras. Kluwer, Dordrecht, 1989.Google Scholar
[8] Helemskii, A. Ya., Lectures and exercises on functional analysis. Transl. Math. Monogr. 233 , Amer. Math. Soc., Providence, RI, 2006.Google Scholar
[9] Helemskii, A. Ya., Extreme flatness of normed modules and Arveson–Wittstock type theorems. J. Operator Theory 64(2010), 101–112.Google Scholar
[10] Helemskii, A. Ya., Metric version of flatness and Hahn-Banach type theorems for normed modules over sequence algebras. Stud. Math., 2012, to appear.Google Scholar
[11] Köthe, G., Hebbare lokalkonvexe Räume. Math. Ann. 165(1966), 181–195. http://dx.doi.org/10.1007/BF01343797 Google Scholar
[12] Löwig, H., Über die Dimension linearer Räume. Stud. Math. 5(1934), 18–23.Google Scholar
[13] Semadeni, Z., Banach spaces of continuous functions. Polish Scientific Publishers,Warsaw, 1971.Google Scholar
[14] Wittstock, G., Injectivity of the module tensor product of semi-Ruan modules. J. Operator Theory 65(2011), 87–113.Google Scholar
[15] Wojtaszczyk, P., Banach spaces for analysts. Cambridge Stud. Adv. Math. 25, Cambridge Univ. Press, Cambridge, 1991.Google Scholar