Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T14:29:55.327Z Has data issue: false hasContentIssue false
  • English
  • Français

Faithfulness of Actions on Riemann-Roch Spaces

Published online by Cambridge University Press:  20 November 2018

Bernhard Köck  and
Joseph Tait
Bernhard Köck
Affiliation:
Mathematical Sciences, University of Southampton, Southampton SO17 1TJ, United Kingdom e-mail: B.Koeck@soton.ac.uk, Joe.Tait@soton.ac.uk
Joseph Tait
Affiliation:
Mathematical Sciences, University of Southampton, Southampton SO17 1TJ, United Kingdom e-mail: B.Koeck@soton.ac.uk, Joe.Tait@soton.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a faithful action of a finite group $G$ on an algebraic curve 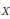$X$ of genus 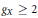$gx\,\ge \,2$, we give explicit criteria for the induced action of $G$ on the Riemann–Roch space 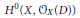${{H}^{0}}\left( X,\,{{\mathcal{O}}_{X}}\left( D \right) \right)$ to be faithful, where 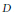$D$ is a $G$-invariant divisor on 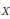$X$ of degree at least 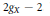${{2}_{gX}}\,-\,2$. This leads to a concise answer to the question of when the action of $G$ on the space 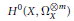${{H}^{0}}\left( X,\,\Omega _{X}^{\otimes m} \right)$ of global holomorphic polydifferentials of order 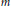$m$ is faithful. If 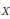$X$ is hyperelliptic, we provide an explicit basis of 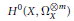${{H}^{0}}\left( X,\,\Omega _{X}^{\otimes m} \right)$. Finally, we give applications in deformation theory and in coding theory and discuss the analogous problem for the action of $G$ on the first homology 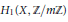${{H}_{1}}\left( X,\,\mathbb{Z}/m\mathbb{Z} \right)$ if 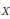$X$ is a Riemann surface.

Keywords

14H3030F3014L3014D1511R32faithful actionsRiemann-Roch spacespolydifferentialshyperelliptic curvesequivariant deformation theoryGoppa codeshomology
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 4 , 01 August 2015 , pp. 848 - 869
Copyright
Copyright © Canadian Mathematical Society 2015

References

[BM] Bertin, J. and Mézard, A., Déformations formelles des revêtements sauvagement ramifiés de courbes algébriques. Invent. Math. 141(2000), no. 1, 195–238.http://dx.doi.org/10.1007/s002220000071 Google Scholar
[Bor] Borne, N., Cohomology of G-sheaves in positive characteristic. Adv. Math. 201(2006), no. 2, 454–515.http://dx.doi.org/10.1016/j.aim.2005.03.002 Google Scholar
[Bro] Broughton, S. A., The homology and higher representations of the automorphism group of a Riemann surface. Trans. Amer. Math. Soc. 300(1987), no. 1, 153–158.http://dx.doi.org/10.1090/S0002-9947-1987-0871669-0 Google Scholar
[CW] Chevalley, C. and Weil, A., Über das Verhalten der integrale 1. Gattung bei automorphismen des Funktionenkörpers. Abh. Math. Sem. Univ. Hamb. 10(1934), no. 1, 358–361.http://dx.doi.org/10.1007/BF02940687 Google Scholar
[FGM+] Friedlander, H., Garton, D., Malmskog, Beth, Pries, R., and Weir, C., The a-numbers of Jacobians of Suzuki curves. Proc. Amer. Math. Soc. 141(2013), no. 9, 3019–3028. http://dx.doi.org/10.1090/S0002-9939-2013-11581-9 Google Scholar
[FK] Farkas, H. M. and Kra, I., Riemann surfaces. Graduate Texts in Mathematics, 71, Springer-Verlag, New York, 1980.Google Scholar
[FW] Fischbacher-Weitz, H. B., Equivariant Riemann-Roch theorems for curves over perfect fields. Ph.D.Thesis, University of Southampton, 2008.Google Scholar
[FWK] Fischbacher-Weitz, H. and Köck, B., Equivariant Riemann-Roch theorems for curves over perfect fields. Manuscripta Math. 128(2009), no. 1, 89–105.http://dx.doi.org/10.1007/s00229-008-0218-3 Google Scholar
[GJK] Glass, D., Joyner, D., and Ksir, A., Codes from Riemann-Roch spaces for y2 = xp −x over GF(p). Int. J. Inf. Coding Theory 1(2010), no. 3, 298–312.http://dx.doi.org/10.1504/IJICOT.2010.032545 Google Scholar
[GK] Giulietti, M. and Korchmáros, G., On automorphism groups of certain Goppa codes. Des. Codes Cryptogr. 47(2008), no. 1–3, 177–190.http://dx.doi.org/10.1007/s10623-007-9110-5 Google Scholar
[Har] Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer-Verlag, New York, 1977.Google Scholar
[Hor] Hortsch, R., On the canonical representation of curves in positive characteristic. New York J. Math. 18(2012), 911–924.Google Scholar
[HS] Haas, A. and Susskind, P., The geometry of the hyperelliptic involution in genus two. Proc. Amer. Math. Soc. 105(1989), no. 1, 159–165.http://dx.doi.org/10.1090/S0002-9939-1989-0930247-2 Google Scholar
[JK] Joyner, D. and Ksir, A., Automorphism groups of some AG codes. IEEE Trans. Inform. Theory 52(2006), no. 7, 3325–3329.http://dx.doi.org/10.1109/TIT.2006.876243 Google Scholar
[Kan] Kani, E., The Galois-module structure of the space of holomorphic differentials of a curve. J. Reine Angew. Math. 367(1986), 187–206.http://dx.doi.org/10.1515/crll.1986.367.187 Google Scholar
[Kar] Karanikolopoulos, S., On holomorphic polydifferentials in positive characteristic. Math. Nachr. 285(2012), no. 7, 852–877. http://dx.doi.org/10.1002/mana.201000114 Google Scholar
[KaKo] Karanikolopoulos, S. and Kontogeorgis, A., Representation of cyclic groups in positive characteristic and Weierstrass semigroups. J. Number Theory 133(2013), no. 1, 158–175.http://dx.doi.org/10.1016/j.jnt.2012.05.039 Google Scholar
[Köc] Köck, B., Galois structure of Zariski cohomology for weakly ramified covers of curves. Amer. J. Math. 126(2004), no. 5, 1085–1107.http://dx.doi.org/10.1353/ajm.2004.0037 Google Scholar
[KöKo] Köck, B. and Kontogeorgis, A., Quadratic differentials and equivariant deformation theory of curves. Ann. Inst. Fourier (Grenoble) 62(2012), no. 3, 1015–1043.http://dx.doi.org/10.5802/aif.2715 Google Scholar
[Kon] Kontogeorgis, A., Polydifferentials and the deformation functor of curves with automorphisms. J.Pure Appl. Algebra 210(2007), no. 2, 551–558.http://dx.doi.org/10.1016/j.jpaa.2006.10.015 Google Scholar
[Lew] Lewittes, J., Automophisms of compact Riemann surfaces. Amer. J. Math. 85(1963), 734–752.http://dx.doi.org/10.2307/2373117 Google Scholar
[Liu] Liu, Q., Algebraic geometry and arithmetic curves. Oxford Graduate Texts in Mathematics, 6, Oxford Science Publications, Oxford University Press, Oxford, 2002.Google Scholar
[Nak1] Nakajima, S., Action of an automorphism of order p on cohomology groups of an algebraic curve. J. Pure Appl. Algebra 42(1986), no. 1, 85–94.http://dx.doi.org/10.1016/0022-4049(86)90062-9 Google Scholar
[Nak2] Nakajima, S., Galois module structure of cohomology groups for tamely ramified coverings of algebraic varieties. J. Number Theory 22(1986), no. 1, 115–123.http://dx.doi.org/10.1016/0022-314X(86)90032-6 Google Scholar
[Ser] Serre, J.-P., Local fields. Graduate Texts in Mathematics, 67, Springer-Verlag, New York, 1979.Google Scholar
[Sil] Silverman, J. H., The arithmetic of elliptic curves. Second ed., Graduate Texts in Mathematics, 106, Springer, Dordrecht, 2009.Google Scholar
[Sti] Stichtenoth, H., Algebraic function fields and codes. Second ed., Graduate Texts in Mathematics, 254, Springer-Verlag, Berlin, 2009.Google Scholar
[VM] Valentini, R. C. and Madan, M. L., Automorphisms and holomorphic differentials in characteristic p. J. Number Theory 13(1981), no. 1, 106–115.http://dx.doi.org/10.1016/0022-314X(81)90032-9 Google Scholar