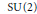Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T04:21:59.023Z Has data issue: false hasContentIssue false
  • English
  • Français

Floer Homology for Knots and $\text{SU(2)}$-Representations for Knot Complements and Cyclic Branched Covers

Published online by Cambridge University Press:  20 November 2018

Olivier Collin
Olivier Collin*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC email: collin@math.ubc.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article, using 3-orbifolds singular along a knot with underlying space a homology sphere ${{Y}^{3}}$, the question of existence of non-trivial and non-abelian 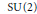$\text{SU(2)}$-representations of the fundamental group of cyclic branched covers of ${{Y}^{3}}$ along a knot is studied. We first use Floer Homology for knots to derive an existence result of non-abelian 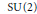$\text{SU(2)}$-representations of the fundamental group of knot complements, for knots with a non-vanishing equivariant signature. This provides information on the existence of non-trivial and non-abelian 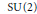$\text{SU(2)}$-representations of the fundamental group of cyclic branched covers. We illustrate the method with some examples of knots in 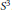${{S}^{3}}$.

Keywords

57M5757M1257M2557M05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 2 , 01 April 2000 , pp. 293 - 305
Copyright
Copyright © Canadian Mathematical Society 2000

References

[AM] Akbulut, S. and McCarthy, J., Casson's Invariant for Oriented Homology 3-spheres. Princeton University Press, New Jersey, 1990.Google Scholar
[BM] Bass, H. and Morgan, J., The Smith Conjecture. Academic Press, New York, 1984.Google Scholar
[BZ] Boileau, M. and Zimmermann, B., The π-orbifold Group of a Link. Math. Z. 200(1989), 187–208.Google Scholar
[Bur] Burde, G., SU(2)-representation spaces for 2-bridge knot groups. Math. Ann. 288(1990), 103–119.Google Scholar
[Co1] Collin, O., Gauge Theory for 3-orbifolds and Knots. D. Phil. Thesis, University of Oxford, 1997.Google Scholar
[Co2] Collin, O., Floer Homology for Orbifolds and Gauge Theory Knot Invariants. In: Proceedings of Knots ‘96, World Scientific Publishing Co., Singapore, 1997, 201–212.Google Scholar
[CS] Collin, O. and Steer, B., Instanton Floer Homology for Knots via 3-orbifolds. J. Differential. Geom., to appear.Google Scholar
[CL] Cooper, D. and Long, D., Representing Knot Groups into SL(2, C). Proc. Amer.Math. Soc. 116(1992), 547–549.Google Scholar
[EN] Eisenbud, D. and Neumann, W., Three-dimensional Link Theory and Invariants of Plane Curve Singularities. Princeton University Press, Princeton, 1985.Google Scholar
[FS] Fintushel, R. and Stern, R., Instanton homology of Seifert fibred homology 3-spheres. Proc. London Math. Soc. 61(1990), 109–137.Google Scholar
[Flo] Floer, A., An Instanton Invariant for 3-manifolds. Comm. Math. Phys. 118(1988), 215–240.Google Scholar
[Fox] Fox, R., The Homology Characters of the Cyclic Coverings of the Knots of Genus One.. Ann. of Math. 71(1960), 187–196.Google Scholar
[He1] Herald, C., Legendrian Cobordism and Chern-Simons Theory for 3-manifolds with Boundary. Comm. Anal. Geom. 2(1994), 337–413.Google Scholar
[He2] Herald, C., Existence of Irreducible Representations ofHomology Knot ComplementsWith Non-constant Equivariant Signature. Math. Ann. 309(1997), 21–35.Google Scholar
[HK] Heusener, M. and Kroll, M., Deforming Abelian SU(2)-representations of Knot Groups. Comment. Math. Helv. 73(1998), 480–498.Google Scholar
[Kir] Kirby, R., Problems in Low-Dimensional Topology. In: Geometric Topology—Proceedings of the 1993 Georgia International Topology Conference 2, International Press, Cambridge, MA, 1997, 35–473.Google Scholar
[KK] Kirk, P. and Klassen, E., Chern-Simons Invariants for 3-manifolds and Representation Spaces of Knot Groups. Math. Ann. 287(1990), 343–367.Google Scholar
[Kla] Klassen, E., Representation Spaces of Knot Groups in SU(2). Trans. Amer. Math. Soc. 326(1991), 795–828.Google Scholar
[Le] Le, D., Sur les Noeuds Algébriques. Comp. Math. 25(1972), 281–321.Google Scholar
[Li1] Litherland, R., Signatures of Iterated Torus Knots. In: Topology of Low-dimensional Manifolds, Proceedings, Sussex 1977, Lecture Notes in Math. 722, Springer-Verlag, Berlin, 1979, 71–84.Google Scholar
[Li2] Litherland, R., Cobordism of Satellite Knots. Contemp.Math. 35(1984), 327–362.Google Scholar
[Rat] Ratcliffe, J., Foundations of Hyperbolic Manifolds. Springer-Verlag, New York, 1994.Google Scholar
[Rol] Rolfsen, D., Knots and Links. Publish or Perish, Houston, 1990.Google Scholar