Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fofanova, T. S.
1968.
Isotone mapping of free lattices.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 4,
Issue. 4,
p.
734.
Adams, M. E.
and
Kelly, David
1977.
Disjointness conditions in free products of lattices.
Algebra Universalis,
Vol. 7,
Issue. 1,
p.
245.
1978.
General Lattice Theory.
Vol. 75,
Issue. ,
p.
316.
Katriňák, Tibor
1982.
Freep-algebras.
Algebra Universalis,
Vol. 15,
Issue. 1,
p.
176.
Katriňák, Tibor
1984.
Splittingp-algebras.
Algebra Universalis,
Vol. 18,
Issue. 2,
p.
199.
Cz�dli, G�bor
and
Day, Alan
1984.
Horn sentences with (W) and weak Mal'cev conditions.
Algebra Universalis,
Vol. 19,
Issue. 2,
p.
217.
Koubek, V.
and
Sichler, J.
1985.
Quotients of rigid (0,1)-lattices.
Archiv der Mathematik,
Vol. 44,
Issue. 5,
p.
403.
Freese, Ralph
1989.
Finitely presented lattices: canonical forms and the covering relation.
Transactions of the American Mathematical Society,
Vol. 312,
Issue. 2,
p.
841.
Freese, Ralph
1990.
Lattices, Semigroups, and Universal Algebra.
p.
67.
Ježek, J.
and
Slavík, V.
1990.
Free lattices over join-trivial partial lattices.
Algebra Universalis,
Vol. 27,
Issue. 1,
p.
10.
Adams, M. E.
1990.
The Dilworth Theorems.
p.
79.
Czédli, G.
1991.
On the word problem of lattices with the help of graphs.
Periodica Mathematica Hungarica,
Vol. 23,
Issue. 1,
p.
49.
Katrińák, Tibor
and
Ševčovič, Daniel
1991.
Projectivep-algebras.
Algebra Universalis,
Vol. 28,
Issue. 2,
p.
280.
Koubek, Václav
1991.
Homomorphisms of (0, 1)-lattices with a given sublattice and quotient.
Glasgow Mathematical Journal,
Vol. 33,
Issue. 2,
p.
159.
Ševčovič, Daniel
1992.
Bounded endomorphisms of free P-algebras.
Glasgow Mathematical Journal,
Vol. 34,
Issue. 2,
p.
209.
Cz�dli, G�bor
1994.
A horn sentence for involution lattices of quasiorders.
Order,
Vol. 11,
Issue. 4,
p.
391.
Stumme, Gerd
1997.
Free Distributive Completions of Partial Complete Lattices.
Order,
Vol. 14,
Issue. 2,
p.
179.
Katriňák, Tibor
1998.
Free distributive P-algebras: a new approach.
Glasgow Mathematical Journal,
Vol. 40,
Issue. 3,
p.
333.
Wehrung, Friedrich
2003.
Forcing extensions of partial lattices.
Journal of Algebra,
Vol. 262,
Issue. 1,
p.
127.
Harding, John
2008.
κ-Complete Uniquely Complemented Lattices.
Order,
Vol. 25,
Issue. 2,
p.
121.

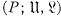 generated by the partially ordered set
generated by the partially ordered set 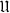 of finite subsets of
of finite subsets of 