Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T02:29:41.494Z Has data issue: false hasContentIssue false
  • English
  • Français

From Steklov to Neumann and Beyond, via Robin: The Szegő Way

Part of: Spectral theory and eigenvalue problems Geometric function theory

Published online by Cambridge University Press:  07 March 2019

Pedro Freitas  and
Richard S. Laugesen
Pedro Freitas
Affiliation:
Departamento de Matemática, Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais 1, P-1049-001 Lisboa, Portugal Grupo de Física Mátematica, Faculdade de Ciências, Universidade de Lisboa, Campo Grande, Edifício C6, P-1749-016 Lisboa, Portugal Email: psfreitas@fc.ul.pt
Richard S. Laugesen
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, USA Email: Laugesen@illinois.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The second eigenvalue of the Robin Laplacian is shown to be maximal for the disk among simply-connected planar domains of fixed area when the Robin parameter is scaled by perimeter in the form 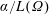$\unicode[STIX]{x1D6FC}/L(\unicode[STIX]{x1D6FA})$, and $\unicode[STIX]{x1D6FC}$ lies between 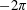$-2\unicode[STIX]{x1D70B}$ and 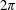$2\unicode[STIX]{x1D70B}$. Corollaries include Szegő’s sharp upper bound on the second eigenvalue of the Neumann Laplacian under area normalization, and Weinstock’s inequality for the first nonzero Steklov eigenvalue for simply-connected domains of given perimeter.

The first Robin eigenvalue is maximal, under the same conditions, for the degenerate rectangle. When area normalization on the domain is changed to conformal mapping normalization and the Robin parameter is positive, the maximiser of the first eigenvalue changes back to the disk.

Keywords

RobinNeumannSteklovvibrating membraneabsorbing boundary conditionconformal mapping

MSC classification

Primary: 35P15: Estimation of eigenvalues, upper and lower bounds
Secondary: 30C70: Extremal problems for conformal and quasiconformal mappings, variational methods
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 4 , August 2020 , pp. 1024 - 1043
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported by the Fundação para a Ciência e a Tecnologia (Portugal) through project PTDC/MAT-CAL/4334/2014 (Pedro Freitas), by a grant from the Simons Foundation (#429422 to Richard Laugesen), by travel support for Laugesen from the American Institute of Mathematics to the workshop on Steklov Eigenproblems (April–May 2018), and support from the University of Illinois Scholars’ Travel Fund.

References

Ashbaugh, M. S. and Benguria, R. D., More bounds on eigenvalue ratios for Dirichlet Laplacians in N dimensions. SIAM J. Math. Anal. 24(1993), no. 6, 1622–1651. https://doi.org/10.1137/0524091Google Scholar
Bossel, M.-H., Membranes élastiquement liées: Extension du théoréme de Rayleigh-Faber-Krahn et de l’inégalité de Cheeger. C. R. Acad. Sci. Paris Sér. I Math. 302(1986), 47–50.Google Scholar
Brock, F., An isoperimetric inequality for eigenvalues of the Stekloff problem. ZAMM Z. Angew. Math. Mech. 81(2001), no. 1, 69–71. doi:10.1002/1521-4001(200101)81:1 <69::AID-ZAMM69 >3.0.CO;2-#3.0.CO;2-#>Google Scholar
Bucur, D., Freitas, P., and Kennedy, J., The Robin problem. In: Shape optimization and spectral theory. De Gruyter Open, Warsaw/Berlin, 2017.Google Scholar
Bucur, D., Ferone, V., Nitsch, C., and Trombetti, C., Weinstock inequality in higher dimensions. J. Differential Geom.. to appear. arxiv:1710.04587Google Scholar
Bucur, D., Ferone, V., Nitsch, C., and Trombetti, C., The quantitative Faber-Krahn inequality for the Robin Laplacian. J. Differential Equations 264(2018), no. 7, 4488–4503. https://doi.org/10.1016/j.jde.2017.12.014Google Scholar
Bucur, D. and Giacomini, A., A variational approach to the isoperimetric inequality for the Robin eigenvalue problem. Arch. Ration. Mech. Anal. 198(2010), no. 3, 927–961. https://doi.org/10.1007/s00205-010-0298-6Google Scholar
Bucur, D. and Giacomini, A., Faber-Krahn inequalities for the Robin-Laplacian: a free discontinuity approach. Arch. Ration. Mech. Anal. 218(2015), no. 2, 757–824. https://doi.org/10.1007/s00205-015-0872-zGoogle Scholar
Daners, D., A Faber–Krahn inequality for Robin problems in any space dimension. Math. Ann. 335(2006), 767–785. https://doi.org/10.1007/s00208-006-0753-8Google Scholar
Duren, P. L., Theory of H p spaces. Corrected and expanded ed. Dover, Mineola, New York, 2000.Google Scholar
Ferone, V., Nitsch, C., and Trombetti, C., On a conjectured reversed Faber–Krahn inequality for a Steklov-type Laplacian eigenvalue. Commun. Pure Appl. Anal. 14(2015), 63–82. https://doi.org/10.3934/cpaa.2015.14.63Google Scholar
Freitas, P. and Kennedy, J. B., Extremal domains and Pólya-type inequalities for the Robin Laplacian on rectangles and unions of rectangles. Int. Math. Res. Not. IMRN. to appear. arxiv:1805.10075Google Scholar
Freitas, P. and Krejčiřík, D., The first Robin eigenvalue with negative boundary parameter. Adv. Math. 280(2015), 322–339. https://doi.org/10.1016/j.aim.2015.04.023Google Scholar
Freitas, P. and Laugesen, R. S., From Neumann to Steklov and beyond, via Robin: the Weinberger way. arxiv:1810.07461Google Scholar
Girouard, A. and Polterovich, I., Shape optimization for low Neumann and Steklov eigenvalues. Math. Methods Appl. Sci. 33(2010), 501–516. https://doi.org/10.1002/mma.1222Google Scholar
Girouard, A. and Polterovich, I., Spectral geometry of the Steklov problem. In: Shape optimization and spectral theory. De Gruyter Open, Warsaw/Berlin, 2017.Google Scholar
Henrot, A., Shape optimization and spectral theory. De Gruyter Open, Warsaw, 2017.Google Scholar
Hersch, J., Quatre propriétés isopérimétriques de membranes sphériques homogènes. C. R. Acad. Sci. Paris Sér. A-B 270(1970), A1645–A1648.Google Scholar
Keady, G. and Wiwatanapataphee, B., Inequalities for the fundamental Robin eigenvalue for the Laplacian on N-dimensional rectangular parallelepipeds. Math. Inequal. Appl. 21(2018), 911–930. https://doi.org/10.7153/mia-2018-21-62Google Scholar
Kennedy, J., An isoperimetric inequality for the second eigenvalue of the Laplacian with Robin boundary conditions. Proc. Amer. Math. Soc. 137(2009), no. 2, 627–633. https://doi.org/10.1090/S0002-9939-08-09704-9Google Scholar
Laugesen, R. S., The Robin Laplacian - spectral conjectures, rectangular theorems. Preprint, arxiv:1905.07658.Google Scholar
Laugesen, R. S., Liang, J., and Roy, A., Sums of magnetic eigenvalues are maximal on rotationally symmetric domains. Ann. Henri Poincaré 13(2012), no. 4, 731–750. https://doi.org/10.1007/s00023-011-0142-zGoogle Scholar
Laugesen, R. S. and Morpurgo, C., Extremals for eigenvalues of Laplacians under conformal mapping. J. Funct. Anal. 155(1998), no. 1, 64–108. https://doi.org/10.1006/jfan.1997.3222Google Scholar
Laugesen, R. S. and Siudeja, B. A., Sums of Laplace eigenvalues—rotationally symmetric maximizers in the plane. J. Funct. Anal. 260(2011), no. 6, 1795–1823. https://doi.org/10.1016/j.jfa.2010.12.018Google Scholar
Laugesen, R. S. and Siudeja, B. A., Sums of Laplace eigenvalues: rotations and tight frames in higher dimensions. J. Math. Phys. 52(2011), no. 9, 093703. https://doi.org/10.1063/1.3635379Google Scholar
Laugesen, R. S. and Siudeja, B. A., Sharp spectral bounds on starlike domains. J. Spectr. Theory 4(2014), no. 2, 309–347. https://doi.org/10.4171/JST/71Google Scholar
NIST Digital Library of Mathematical Functions. Release 1.0.18 of 2018-03-27. F. W. J. Olver, A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, and B. V. Saunders, eds. http://dlmf.nist.gov/.Google Scholar
Pólya, G. and Szegő, G., Isoperimetric inequalities in mathematical physics. Princeton University Press, Princeton, NJ, 1951.Google Scholar
Pommerenke, C., Boundary behaviour of conformal maps. (Grundlehren der Mathematischen Wissenschaften, 299), Springer–Verlag, Berlin, 1992. https://doi.org/10.1007/978-3-662-02770-7Google Scholar
Szegő, G., Inequalities for certain eigenvalues of a membrane of given area. J. Rational Mech. Anal. 3(1954), 343–356. https://doi.org/10.1512/iumj.1954.3.53017Google Scholar
Weinberger, H. F., An isoperimetric inequality for the N-dimensional free membrane problem. J. Rational Mech. Anal. 5(1956), 633–636. https://doi.org/10.1512/iumj.1956.5.55021Google Scholar
Weinstock, R., Inequalities for a classical eigenvalue problem. J. Rational Mech. Anal. 3(1954), 745–753. https://doi.org/10.1512/iumj.1954.3.53036Google Scholar