Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-08T18:50:05.313Z Has data issue: false hasContentIssue false
  • English
  • Français

Galois Theory of Essential Extensions of Modules

Published online by Cambridge University Press:  20 November 2018

Sylvia Wiegand
Sylvia Wiegand*
Affiliation:
The University of Wisconsin, Madison, Wisconsin; The University of Nebraska, Lincoln, Nebraska
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to exploit an analogy between algebraic extensions of fields and essential extensions of modules, in which the role of the algebraic closure of a field F is played by the injective hull H(M) of a unitary left R-module M. (The notion of * ‘algebraic’ extensions of general algebraic systems has been studied by Shoda; see, for example [5].)

In this analogy, the role of a polynomial p(x) is played by a homomorphism of R-modules

(1)

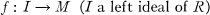
which will be called an ideal homomorphism into M. The process of solving the equation p(x) = 0 in F, or in an algebraic extension of F, will be replaced by the process of extending an ideal homomorphism (1) to a homomorphism F* from R into M, or into an essential extension of M.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 4 , August 1972 , pp. 573 - 579
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Gill, D., Almost maximal valuation rings, J. London Math. Soc. 4 (1971), 140–146.Google Scholar
2. Gilmer, R., A note on the algebraic closure of a field, Amer. Math. Monthly 75 (1968), 1101–1102.Google Scholar
3. Matlis, E., Injective modules over Prüfer rings, Nagoya Math J. 15 (1959), 57–69.Google Scholar
4. Rosenberg, A. and Zelinsky, D., Finiteness of the injective hull, Math. Z. 70 (1959), 372–380.Google Scholar
5. Shoda, K., Zur theorie der algebraischen Erweiterungen, Osaka Math. J. 4 (1952), 133–144.Google Scholar