Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-06-08T07:39:26.137Z Has data issue: false hasContentIssue false
  • English
  • Français

H∞ Functional Calculus and Mikhlin-Type Multiplier Conditions

Published online by Cambridge University Press:  20 November 2018

José E. Galé  and
Pedro J. Miana
José E. Galé
Affiliation:
Departamento de Matem´aticas, Facultad de Ciencias, Universidad de Zaragoza, 50009 Zaragoza, Spain e-mail:gale@unizar.espjmiana@unizar.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 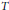$T$ be a sectorial operator. It is known that the existence of a bounded (suitably scaled) 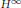${{H}^{\infty }}$ calculus for 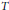$T$, on every sector containing the positive half-line, is equivalent to the existence of a bounded functional calculus on the Besov algebra 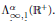$\Lambda _{\infty ,1}^{\alpha }({{\mathbb{R}}^{+}})$. Such an algebra includes functions defined byMikhlin-type conditions and so the Besov calculus can be seen as a result on multipliers for 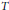$T$. In this paper, we use fractional derivation to analyse in detail the relationship between 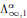$\Lambda _{\infty ,1}^{\alpha }$ and Banach algebras of Mikhlin-type. As a result, we obtain a new version of the quoted equivalence.

Keywords

47A6047D0346J1526A33 47L6047B4843A22functional calculusfractional calculusMikhlin multipliersanalytic semigroupsunbounded operatorsquasimultipliers
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 5 , October 2008 , pp. 1010 - 1027
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Bergh, J. and Löfström, J., Interpolation Spaces. Grundlehren der Mathematischen Wissenschaften 223, Springer-Verlag, Berlin, 1976.Google Scholar
[2] Carbery, A., Gasper, G., andTrebels, W., On localized potential spaces. J. Approx. Theory 48(1986), no. 3, 251–261.Google Scholar
[3] Cossar, J., A theorem on Cesàro summability. J. London Math. Soc. 16(1941), 56–68.Google Scholar
[4] Cowling, M., Doust, I., McIntosh, A., and Yagi, A., Banach operators with a bounded H ∞ functional calculus. J. Austral. Math. Soc. Ser. A 60(1996), no. 1, 51–89.Google Scholar
[5] Duong, X. T., From the L 1 norms of the complex heat kernels to a Hörmander multiplier theorem for sub-Laplacians on nilpotent Lie groups. Pacific J. Math. 173(1996), no. 2, 413–424.Google Scholar
[6] Duong, X. T., Ouhabaz, E. M., and Sikora, A., Plancherel-type estimates and sharp spectral multipliers. J. Funct. Anal. 196(2002), no. 2, 443–485.Google Scholar
[7] Esterle, J., Quasimultipliers, representations of H∞ , and the closed ideal problem for commutative Banach algebras. In: Radical Banach Algebras and Automatic Continuity. Lecture Notes in Math. 975, Springer, Berlin 1983, pp. 66–162.Google Scholar
[8] Galé, J. E., A notion of analytic generator for groups of unbounded operators. In: Topological Algebras, Their Applications, and Related Topics. Banach Center Pub. 67, Polish Acad. Sci.,Warsaw, 2005, pp. 185–197.Google Scholar
[9] Galé, J. E. and Miana, P. J., One-parameter groups of regular quasimultipliers. J. Funct. Anal. 237(2006), no. 1, 1–53.Google Scholar
[10] Galé, J. E. and Pytlik, T., Functional calculus for infinitesimal generators of holomorphic semigroups. J. Funct. Anal. 150(1997), no. 2, 307–355.Google Scholar
[11] Gasper, G. andTrebels, W., A characterization of localized Bessel potential spaces and applications to Jacobi and Hankel multipliers. Studia Math. 65(1979), no. 3, 243–278.Google Scholar
[12] McIntosh, A., Operators which have an H1 functional calculus. In: Miniconference on Operator Theory and Partial Differential Equations. Proc. CentreMath. Anal. Austral. Nat. Univ. 14, Canberra, 1986, pp. 210–231.Google Scholar
[13] Peetre, J., New Thoughts on Besov Spaces Equations. Duke Univsity Mathematics Series 1, Durham, NC, 1976.Google Scholar
[14] Samko, S. G., Kilbas, A. A., and Marichev, O. I., Fractional integrals and derivatives. Theory and applications. Gordon and Breach, Yverdon, 1993.Google Scholar
[15] Trebels, W., Some Fourier multiplier criteria and the spherical Bochner-Riesz kernel. Rev. Roumaine Math. Pures Appl. 20(1975), no. 10, 1173–1185.Google Scholar
[16] Uiterdijk, M., A functional calculus for analytic generators of C 0 groups. Integral Equations Operator Theory 36(2000), no. 3, 349–369 Google Scholar