1 Introduction
Two of the outstanding conjectures in number theory are the so-called Batyrev–Manin conjecture [Reference Franke, Manin and Tschinkel9] for the density of rational points on open subschemes of Fano varieties with respect to a Weil height, and Malle’s conjecture [Reference Malle14] on the number of number fields having bounded discriminant, fixed degree, and fixed Galois group. Both conjectures assert, roughly, that the number of objects to be counted with an appropriate height at most X satisfy an asymptotic formula of the form
where
![]() $C, \alpha , \beta $
are nonnegative numbers with
$C, \alpha , \beta $
are nonnegative numbers with
![]() $C, \alpha> 0$
, and that
$C, \alpha> 0$
, and that
![]() $C, \alpha , \beta $
can be computed explicitly within their respective geometric and arithmetic frameworks.
$C, \alpha , \beta $
can be computed explicitly within their respective geometric and arithmetic frameworks.
In a recent article, J. Ellenberg, M. Satriano, and D. Zureick-Brown extend the theory of heights to algebraic stacks. They formulate bold conjectures that encompasses both the Batyrev–Manin and Malle conjectures as special cases [Reference Ellenberg, Satriano and Zureick-Brown6, Main Conjecture]. While the Manin and Malle conjectures are well studied, comparatively little is known about the behavior of rational points on algebraic stacks.
In this article, we study heights on stacky curves, analogues of smooth projective algebraic curves defined over
![]() $\mathbb {Q}$
. The height functions we develop on stacky curves are completely explicit and can be understood in an elementary manner. Further, we will see that natural questions involving stacky curves lead to an equivalent formulation of the
$\mathbb {Q}$
. The height functions we develop on stacky curves are completely explicit and can be understood in an elementary manner. Further, we will see that natural questions involving stacky curves lead to an equivalent formulation of the
![]() $abc$
-conjecture.
$abc$
-conjecture.
The Stacky Batyrev–Manin-Malle Conjecture is still open for smooth one-dimensional algebraic stacks. In this article, we focus on stacky curves whose coarse moduli space is
![]() ${\mathbb {P}}^1$
. A key example is
${\mathbb {P}}^1$
. A key example is
![]() ${\mathbb {P}}^1$
endowed with three stacky points of degree
${\mathbb {P}}^1$
endowed with three stacky points of degree
![]() $\frac {1}{2}$
and the height given by the anti-canonical bundle. This algebraic stack may be thought of as the usual projective line, except the points
$\frac {1}{2}$
and the height given by the anti-canonical bundle. This algebraic stack may be thought of as the usual projective line, except the points
![]() $0,1,\infty $
have been replaced with “stacky” points that have degree
$0,1,\infty $
have been replaced with “stacky” points that have degree
![]() $\frac {1}{2}$
rather the
$\frac {1}{2}$
rather the
![]() $1$
. Alternatively, one may consider the M-curve as described by Darmon, here the points
$1$
. Alternatively, one may consider the M-curve as described by Darmon, here the points
![]() $0,1,\infty $
have multiplicity 2. The key observation is that a point of multiplicity m has degree
$0,1,\infty $
have multiplicity 2. The key observation is that a point of multiplicity m has degree
![]() $\frac {1}{m}$
.
$\frac {1}{m}$
.
In the case of
![]() ${\mathbb {P}}^1$
with three half points, rational points on this stack can be thought of as rational points on
${\mathbb {P}}^1$
with three half points, rational points on this stack can be thought of as rational points on
![]() ${\mathbb {P}}^1$
. The anti-canonical height function can now be explicitly written after normalization as
${\mathbb {P}}^1$
. The anti-canonical height function can now be explicitly written after normalization as
Put
![]() $N(T)=\{(a:b)\in {\mathbb {P}}^1({\mathbb {Q}})\colon H(a:b)\leq T\}$
. Then we have the following theorem.
$N(T)=\{(a:b)\in {\mathbb {P}}^1({\mathbb {Q}})\colon H(a:b)\leq T\}$
. Then we have the following theorem.
Theorem 1.1 There are positive numbers
![]() $c_1,c_2,c_3$
such that
$c_1,c_2,c_3$
such that
for all
![]() $T>c_3$
.
$T>c_3$
.
The above estimate proves the stacky Batyrev–Manin conjecture for the anti-canonical height on
![]() ${\mathbb {P}}^1$
with three half points.
${\mathbb {P}}^1$
with three half points.
We note that P. Le Boudec has independently proved this statement in a private communication.
Let
![]() $\mathfrak {X}$
be a proper smooth stacky curve defined over
$\mathfrak {X}$
be a proper smooth stacky curve defined over
![]() ${\mathbb {Q}}$
that has coarse space
${\mathbb {Q}}$
that has coarse space
![]() ${\mathbb {P}}^1$
. The rational points of this stack are the rational points of
${\mathbb {P}}^1$
. The rational points of this stack are the rational points of
![]() ${\mathbb {P}}^1$
. As in the classical case, there is a canonical line bundle
${\mathbb {P}}^1$
. As in the classical case, there is a canonical line bundle
![]() $K_{\mathfrak {X}}$
on
$K_{\mathfrak {X}}$
on
![]() $\mathfrak {X}$
. The theory described in [Reference Ellenberg, Satriano and Zureick-Brown6] provides a height function for every line bundle on
$\mathfrak {X}$
. The theory described in [Reference Ellenberg, Satriano and Zureick-Brown6] provides a height function for every line bundle on
![]() $\mathfrak {X}$
. Therefore, as in the case of algebraic curves, we may consider the anti-canonical height
$\mathfrak {X}$
. Therefore, as in the case of algebraic curves, we may consider the anti-canonical height
![]() $H_{-K_{\mathfrak {X}}}$
. This anti-canonical height is analogous to the anti-canonical height on a Fano variety in the usual Batyrev–Manin conjecture. A natural question is when does the anti-canonical height of
$H_{-K_{\mathfrak {X}}}$
. This anti-canonical height is analogous to the anti-canonical height on a Fano variety in the usual Batyrev–Manin conjecture. A natural question is when does the anti-canonical height of
![]() $\mathfrak {X}$
satisfy the Northcott property. It turns out that the stacky Euler characteristic answers this question. The Euler characteristic of
$\mathfrak {X}$
satisfy the Northcott property. It turns out that the stacky Euler characteristic answers this question. The Euler characteristic of
![]() $\mathfrak {X}$
is defined as
$\mathfrak {X}$
is defined as
If
![]() $\mathfrak {X}$
is
$\mathfrak {X}$
is
![]() ${\mathbb {P}}^1$
with stacky points
${\mathbb {P}}^1$
with stacky points
![]() $p_1,...,p_n$
with
$p_1,...,p_n$
with
![]() $\deg p_i=\frac {1}{m_i}$
, then one has the formula
$\deg p_i=\frac {1}{m_i}$
, then one has the formula
 $$ \begin{align} \chi(\mathfrak{X})=2-\sum_{i=1}^n \left(1-\frac{1}{m_i}\right). \end{align} $$
$$ \begin{align} \chi(\mathfrak{X})=2-\sum_{i=1}^n \left(1-\frac{1}{m_i}\right). \end{align} $$
The ESZ-B height associated with
![]() $-K_{\mathfrak {X}}$
is then given by the explicit formula
$-K_{\mathfrak {X}}$
is then given by the explicit formula
 $$ \begin{align} H_{-K_{\mathfrak{X}}}(x,y)=\max\{\vert x\vert,\vert y\vert \}^{\chi(\mathfrak{X})}\prod_{i=1}^r\phi_{m_i}(\ell_i(x,y))^{\frac{1}{m_i}}. \end{align} $$
$$ \begin{align} H_{-K_{\mathfrak{X}}}(x,y)=\max\{\vert x\vert,\vert y\vert \}^{\chi(\mathfrak{X})}\prod_{i=1}^r\phi_{m_i}(\ell_i(x,y))^{\frac{1}{m_i}}. \end{align} $$
The functions
![]() $\phi _{m_i}(\ell _i(x,y))$
are generalizations of the functions
$\phi _{m_i}(\ell _i(x,y))$
are generalizations of the functions
![]() $\operatorname {sqf}(\vert x\vert ) ,\operatorname {sqf}(\vert y\vert )$
, and
$\operatorname {sqf}(\vert x\vert ) ,\operatorname {sqf}(\vert y\vert )$
, and
![]() $\operatorname {sqf}(\vert x+y\vert )$
that appear in equation (1.1) (see Section 3 for the precise definitions of the functions
$\operatorname {sqf}(\vert x+y\vert )$
that appear in equation (1.1) (see Section 3 for the precise definitions of the functions
![]() $\ell _i$
and
$\ell _i$
and
![]() $\phi _{m_i}$
). We obtain a similar explicit description for any line bundle on
$\phi _{m_i}$
). We obtain a similar explicit description for any line bundle on
![]() $\mathfrak {X}$
in terms of the functions
$\mathfrak {X}$
in terms of the functions
![]() $\phi _{m_i}$
and
$\phi _{m_i}$
and
![]() $\ell _i$
in Theorem 3.16. For the anti-canonical height, we obtain the following.
$\ell _i$
in Theorem 3.16. For the anti-canonical height, we obtain the following.
Theorem 1.2 Let
![]() $\mathfrak {X}$
be a proper smooth stacky curve defined over
$\mathfrak {X}$
be a proper smooth stacky curve defined over
![]() ${\mathbb {Q}}$
that has coarse space
${\mathbb {Q}}$
that has coarse space
![]() ${\mathbb {P}}^1$
or is isomorphic to a smooth projective curve. Then the anti-canonical height
${\mathbb {P}}^1$
or is isomorphic to a smooth projective curve. Then the anti-canonical height
![]() $H_{-K_{\mathfrak {X}}}$
has the Northcott property if and only if
$H_{-K_{\mathfrak {X}}}$
has the Northcott property if and only if
![]() $\chi (\mathfrak {X})>0$
.
$\chi (\mathfrak {X})>0$
.
The above result tells us that the ESZ-B heights when applied to the tangent bundle recovers the behavior of the Weil heights when applied to the tangent bundle, providing additional evidence that the ESZ-B theory of heights is the correct generalization of the classical theory. In particular, Theorem 1.2 demonstrates that the stacky Batyrev–Manin conjecture of [Reference Ellenberg, Satriano and Zureick-Brown6] is a direct generalization of the classical Batyrev–Manin conjecture for Fano varieties.
Ellenberg, Satriano, and Zureick-Brown have proposed a generalized Vojta’s conjecture applicable to the case of algebraic stacks [Reference Ellenberg, Satriano and Zureick-Brown6, Conjecture 4.23]. In the case of stacky curves, the stacky Vojta conjecture is directly related to when does
![]() $H_{-K_{\mathfrak {X}}}$
to have the Northcott property.
$H_{-K_{\mathfrak {X}}}$
to have the Northcott property.
In [Reference Ellenberg, Satriano and Zureick-Brown6, Section 4.7], it is speculated that [Reference Ellenberg, Satriano and Zureick-Brown6, Conjecture 4.23] for stacky curves should follow from some version of the
![]() $abc$
-conjecture. In the case of algebraic curves, Vojta’s conjecture is known to be equivalent to the
$abc$
-conjecture. In the case of algebraic curves, Vojta’s conjecture is known to be equivalent to the
![]() $abc$
-conjecture. We show that, much like the case of algebraic curves, the stacky analogue of Vojta’s conjecture in the curve case is equivalent to the
$abc$
-conjecture. We show that, much like the case of algebraic curves, the stacky analogue of Vojta’s conjecture in the curve case is equivalent to the
![]() $abc$
-conjecture. We formulate this as follows:
$abc$
-conjecture. We formulate this as follows:
Theorem 1.3 Let
![]() $\mathfrak {X}$
be a proper smooth stacky curve defined over
$\mathfrak {X}$
be a proper smooth stacky curve defined over
![]() ${\mathbb {Q}}$
that has coarse space
${\mathbb {Q}}$
that has coarse space
![]() ${\mathbb {P}}^1$
or is isomorphic to a smooth projective curve. Further, suppose that
${\mathbb {P}}^1$
or is isomorphic to a smooth projective curve. Further, suppose that
![]() $\mathfrak {X}$
has negative Euler characteristic. Then the following statements are equivalent:
$\mathfrak {X}$
has negative Euler characteristic. Then the following statements are equivalent:
-
(1) The
 $abc$
-conjecture holds; and
$abc$
-conjecture holds; and -
(2) For all
 $\mathfrak {X}$
satisfying the hypotheses of the theorem and for all
$\mathfrak {X}$
satisfying the hypotheses of the theorem and for all
 $\delta> 0$
, the function
$\delta> 0$
, the function
 $\mathcal {H}_{-K_{\mathfrak {X}}} \cdot H^\delta $
has Northcott’s property, where
$\mathcal {H}_{-K_{\mathfrak {X}}} \cdot H^\delta $
has Northcott’s property, where
 $H([x,y]) = \max \{|x|, |y|\}$
is the usual height function on
$H([x,y]) = \max \{|x|, |y|\}$
is the usual height function on
 ${\mathbb {P}}^1({\mathbb {Q}})$
.
${\mathbb {P}}^1({\mathbb {Q}})$
.
Theorem 1.3 shows that Conjecture 4.23 in [Reference Ellenberg, Satriano and Zureick-Brown6] is equivalent to the
![]() $abc$
-conjecture, answering a question of Ellenberg, Satriano, and Zureick-Brown. Their conjectures are motivated by the work of P. Vojita, see [Reference Vojta21]
$abc$
-conjecture, answering a question of Ellenberg, Satriano, and Zureick-Brown. Their conjectures are motivated by the work of P. Vojita, see [Reference Vojta21]
In [Reference Ellenberg, Satriano and Zureick-Brown6], the authors wonder if the stacky Vojta conjecture might be more “in reach” for algebraic stacks obtained by rooting along a divisor D on a scheme X. The proof of Theorem 1.3 shows that if there is some
![]() $m\geq 4$
such that item (2) in Theorem 1.3 holds for
$m\geq 4$
such that item (2) in Theorem 1.3 holds for
![]() $\mathfrak {X}_m = \mathfrak {X}({\mathbb {P}}^1 : ((0,1,\infty ) : (m,m,m))$
, then a weak variant of the
$\mathfrak {X}_m = \mathfrak {X}({\mathbb {P}}^1 : ((0,1,\infty ) : (m,m,m))$
, then a weak variant of the
![]() $abc$
-conjecture can be derived. Specifically, there exists a positive number
$abc$
-conjecture can be derived. Specifically, there exists a positive number
![]() $c_m \geq 1$
such that for any co-prime
$c_m \geq 1$
such that for any co-prime
![]() $a,b,c \in {\mathbb {Z}}$
with
$a,b,c \in {\mathbb {Z}}$
with
![]() $a + b = c$
and
$a + b = c$
and
![]() $\varepsilon> 0$
that
$\varepsilon> 0$
that
In particular, any progress on the stacky Vojta conjecture for curves would lead to substantial progress on the
![]() $abc$
-conjecture.
$abc$
-conjecture.
2 A further elaboration of our ideas
In this section, we motivate and describe our main results in more detail, as well as describe our grounds-up height construction.
2.1 An elementary height machine on stacky curves
We define our algebraic stacks in terms of a base variety along with some extra data which are enough to uniquely construct an algebraic stack. A stacky curve defined over a number field K is determined by the following data: A smooth variety X defined over K, and a finite number of stacky points
![]() $P_1,\dots ,P_r$
along with integer multiplicities
$P_1,\dots ,P_r$
along with integer multiplicities
![]() $m_{P_i}=m_i>1$
attached to each point
$m_{P_i}=m_i>1$
attached to each point
![]() $P_i$
. We use the notation
$P_i$
. We use the notation
to denote the stacky curve with multiplicities
![]() $m_{P_i}=m_i$
at the points
$m_{P_i}=m_i$
at the points
![]() $P_i$
. We will write
$P_i$
. We will write
![]() $\mathfrak {X}(X:({\mathbf {a}}, {\mathbf {m}}))$
as an abbreviation. We identify the rational points of the stack
$\mathfrak {X}(X:({\mathbf {a}}, {\mathbf {m}}))$
as an abbreviation. We identify the rational points of the stack
![]() $\mathfrak {X}$
with those of the coarse space, which is just the variety X. That is, we require
$\mathfrak {X}$
with those of the coarse space, which is just the variety X. That is, we require
In [Reference Ellenberg, Satriano and Zureick-Brown6], some care is taken to work with the locus of stacky points on an algebraic stack. In particular, one must contend with the accumulation of infinitely new stacky points. We ignore such difficulties since they are not important in our context.
To obtain an E-S-ZB height on a stacky curve
![]() $\mathfrak {X}(X:({\mathbf {a}},{\mathbf {m}}))$
, we must choose a vector bundle on
$\mathfrak {X}(X:({\mathbf {a}},{\mathbf {m}}))$
, we must choose a vector bundle on
![]() $\mathfrak {X}(X:({\mathbf {a}},{\mathbf {m}}))$
. We will be primarily interested in the stacky curves
$\mathfrak {X}(X:({\mathbf {a}},{\mathbf {m}}))$
. We will be primarily interested in the stacky curves
![]() $\mathfrak {X}({\mathbb {P}}^1_{\mathbb {Q}}: (a_1,m_1),\dots ,(a_r,m_r))$
and the vector bundle being a line bundle. Unless otherwise mentioned, stacky curve
$\mathfrak {X}({\mathbb {P}}^1_{\mathbb {Q}}: (a_1,m_1),\dots ,(a_r,m_r))$
and the vector bundle being a line bundle. Unless otherwise mentioned, stacky curve
![]() $\mathfrak {X}$
will now be of this form. Associated with each stacky point,
$\mathfrak {X}$
will now be of this form. Associated with each stacky point,
![]() $a_i$
is a line bundle
$a_i$
is a line bundle
![]() ${\mathcal {L}}_{a_i}$
and it suffices to consider line bundles of the form
${\mathcal {L}}_{a_i}$
and it suffices to consider line bundles of the form
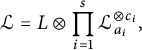 $$\begin{align*}\mathcal{L}=L\otimes \prod_{i=1}^s{\mathcal{L}}_{a_i}^{\otimes c_i},\end{align*}$$
$$\begin{align*}\mathcal{L}=L\otimes \prod_{i=1}^s{\mathcal{L}}_{a_i}^{\otimes c_i},\end{align*}$$
where L is a divisor on
![]() ${\mathbb {P}}^1$
and
${\mathbb {P}}^1$
and
![]() $0\leq c_i\leq m_i-1$
. To associate a height on such a divisor, we associate a height to each
$0\leq c_i\leq m_i-1$
. To associate a height on such a divisor, we associate a height to each
![]() ${\mathcal {L}}_{a_i}^{\otimes c_i}$
and extend linearly. Motivated by [Reference Ellenberg, Satriano and Zureick-Brown6], we develop the following construction. For each stacky point
${\mathcal {L}}_{a_i}^{\otimes c_i}$
and extend linearly. Motivated by [Reference Ellenberg, Satriano and Zureick-Brown6], we develop the following construction. For each stacky point
![]() $a_i = [\alpha _i : \beta _i]$
with
$a_i = [\alpha _i : \beta _i]$
with
![]() $\alpha _i,\beta _i$
coprime integers, we associate to it the linear form
$\alpha _i,\beta _i$
coprime integers, we associate to it the linear form
![]() $\ell _i(x,y) = \alpha _i y- \beta _i x$
. For each
$\ell _i(x,y) = \alpha _i y- \beta _i x$
. For each
![]() $m_i$
, define
$m_i$
, define
![]() $\phi _{m_i}(n)$
is defined to be the smallest positive integer such that
$\phi _{m_i}(n)$
is defined to be the smallest positive integer such that
![]() $n \phi _{m_i}(n)$
is a perfect
$n \phi _{m_i}(n)$
is a perfect
![]() $m_i$
-th power. The height function associated with
$m_i$
-th power. The height function associated with
![]() ${\mathcal {L}}_{a_i}^{\otimes c_i}$
is then
${\mathcal {L}}_{a_i}^{\otimes c_i}$
is then
The linear form
![]() $\ell _i$
takes into account the point
$\ell _i$
takes into account the point
![]() $a_i$
and
$a_i$
and
![]() $\phi _{m_i}$
accounts for the multiplicity of
$\phi _{m_i}$
accounts for the multiplicity of
![]() $a_i$
, while the power
$a_i$
, while the power
![]() $c_i$
accounts for the multiple of
$c_i$
accounts for the multiple of
![]() ${\mathcal {L}}_{a_i}$
. The introduction of the functions
${\mathcal {L}}_{a_i}$
. The introduction of the functions
![]() $\phi _{m_i}$
is due to [Reference Ellenberg, Satriano and Zureick-Brown6] and working with these functions is a key feature of stacky curves with coarse space
$\phi _{m_i}$
is due to [Reference Ellenberg, Satriano and Zureick-Brown6] and working with these functions is a key feature of stacky curves with coarse space
![]() ${\mathbb {P}}^1$
. We define a height function for any divisor
${\mathbb {P}}^1$
. We define a height function for any divisor
![]() $\mathcal {L}=L\otimes \prod _{i=1}^s{\mathcal {L}}_{a_i}^{\otimes c_i}$
on
$\mathcal {L}=L\otimes \prod _{i=1}^s{\mathcal {L}}_{a_i}^{\otimes c_i}$
on
![]() $\mathfrak {X}$
as
$\mathfrak {X}$
as
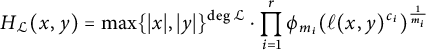 $$ \begin{align} H_{\mathcal{L}}(x,y)=\max\{\vert x\vert,\vert y\vert\}^{\deg {\mathcal{L}}}\cdot \prod_{i=1}^r\phi_{m_i}(\ell(x,y)^{c_i})^{\frac{1}{m_i}} \end{align} $$
$$ \begin{align} H_{\mathcal{L}}(x,y)=\max\{\vert x\vert,\vert y\vert\}^{\deg {\mathcal{L}}}\cdot \prod_{i=1}^r\phi_{m_i}(\ell(x,y)^{c_i})^{\frac{1}{m_i}} \end{align} $$
whenever
![]() $x,y$
are coprime integers. The Euler characteristic of the stacky curve is defined to be the degree of the anti-canonical divisor. If we wish to emphasize in our situation that
$x,y$
are coprime integers. The Euler characteristic of the stacky curve is defined to be the degree of the anti-canonical divisor. If we wish to emphasize in our situation that
![]() $\chi (\mathfrak {X})$
only depends on the vector of multiplicities
$\chi (\mathfrak {X})$
only depends on the vector of multiplicities
![]() ${\mathbf {m}}$
and that the anti-canonical height only depends on
${\mathbf {m}}$
and that the anti-canonical height only depends on
![]() $({\mathbf {a}},{\mathbf {m}})$
, we write
$({\mathbf {a}},{\mathbf {m}})$
, we write
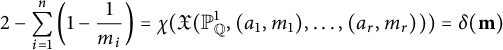 $$ \begin{align} 2 - \sum_{i=1}^n \left(1 - \frac{1}{m_i}\right)=\chi(\mathfrak{X}({\mathbb{P}}^1_{\mathbb{Q}},(a_1,m_1),\ldots,(a_r,m_r)))=\delta({\mathbf{m}})\end{align} $$
$$ \begin{align} 2 - \sum_{i=1}^n \left(1 - \frac{1}{m_i}\right)=\chi(\mathfrak{X}({\mathbb{P}}^1_{\mathbb{Q}},(a_1,m_1),\ldots,(a_r,m_r)))=\delta({\mathbf{m}})\end{align} $$
and
 $$ \begin{align} \max\{\vert x\vert,\vert y\vert \}^{\delta({\mathbf{m}})}\prod_{i=1}^r\phi_{m_i}(\ell_i(x,y))^{\frac{1}{m_i}}=H_{-K_{\mathfrak{X}}}([x:y])=\mathcal{H}_{({\mathbf{a}}, {\mathbf{m}})}(x,y). \end{align} $$
$$ \begin{align} \max\{\vert x\vert,\vert y\vert \}^{\delta({\mathbf{m}})}\prod_{i=1}^r\phi_{m_i}(\ell_i(x,y))^{\frac{1}{m_i}}=H_{-K_{\mathfrak{X}}}([x:y])=\mathcal{H}_{({\mathbf{a}}, {\mathbf{m}})}(x,y). \end{align} $$
2.2 Properties of the anti-canonical E-S-ZB height
 $H_{-K_{\mathfrak {X}}}$
$H_{-K_{\mathfrak {X}}}$
The Northcott property of the naive height on
![]() ${\mathbb {P}}^1$
implies that the ESZ-B anti-canonical height
${\mathbb {P}}^1$
implies that the ESZ-B anti-canonical height
![]() $H_{-K_{\mathfrak {X}}}$
has the Northcott property whenever
$H_{-K_{\mathfrak {X}}}$
has the Northcott property whenever
![]() $\chi (\mathfrak {X})=\delta ({\mathbf {m}})>0$
. On the other hand, if
$\chi (\mathfrak {X})=\delta ({\mathbf {m}})>0$
. On the other hand, if
![]() $\chi (\mathfrak {X})\leq 0$
, then it is not at all obvious whether
$\chi (\mathfrak {X})\leq 0$
, then it is not at all obvious whether
![]() $H_{-K_{\mathfrak {X}}}$
should have the Northcott property. The following question is fundamental: Let
$H_{-K_{\mathfrak {X}}}$
should have the Northcott property. The following question is fundamental: Let
![]() ${\mathcal {L}}$
be a line bundle on
${\mathcal {L}}$
be a line bundle on
![]() $\mathfrak {X}(X: ({\mathbf {a}},{\mathbf {m}}))$
and let
$\mathfrak {X}(X: ({\mathbf {a}},{\mathbf {m}}))$
and let
![]() $H_{{\mathcal {L}}}$
be the associated ESZ-B height. When does
$H_{{\mathcal {L}}}$
be the associated ESZ-B height. When does
![]() $H_{\mathcal {L}}$
have the Northcott property? We will tackle this question when
$H_{\mathcal {L}}$
have the Northcott property? We will tackle this question when
![]() ${\mathcal {L}}=-K_{\mathfrak {X}}$
and
${\mathcal {L}}=-K_{\mathfrak {X}}$
and
![]() $X={\mathbb {P}}^1$
leaving the general case for future study.
$X={\mathbb {P}}^1$
leaving the general case for future study.
Theorem 2.1 Let
![]() $\{a_1, \ldots , a_n\} \subset {\mathbb {P}}_{\mathbb {Q}}^1$
and
$\{a_1, \ldots , a_n\} \subset {\mathbb {P}}_{\mathbb {Q}}^1$
and
![]() ${\mathbf {m}} = (m_1, \ldots , m_n)$
be a vector of multiplicities. Then whenever
${\mathbf {m}} = (m_1, \ldots , m_n)$
be a vector of multiplicities. Then whenever
the anti-canonical height
![]() $H_{-K_{\mathfrak {X}}}$
given by (2.2) on the curve
$H_{-K_{\mathfrak {X}}}$
given by (2.2) on the curve
![]() $\mathfrak {X}({\mathbb {P}}^1 : (a_1, m_1), \ldots , (a_n, m_n))$
fails to have the Northcott property.
$\mathfrak {X}({\mathbb {P}}^1 : (a_1, m_1), \ldots , (a_n, m_n))$
fails to have the Northcott property.
If we assume that the ESZ-B theory should behave roughly like its classical counterpart, we can argue the converse: When
![]() $\chi (\mathfrak {X})\leq 0$
, one should have that
$\chi (\mathfrak {X})\leq 0$
, one should have that
![]() $H_{-K_{\mathfrak {X}}}$
should fail to have the Northcott property. In particular, Theorem 2.1 shows that our arithmetic and geometric intuition prove to be correct when
$H_{-K_{\mathfrak {X}}}$
should fail to have the Northcott property. In particular, Theorem 2.1 shows that our arithmetic and geometric intuition prove to be correct when
![]() $\mathfrak {X}$
has coarse space
$\mathfrak {X}$
has coarse space
![]() ${\mathbb {P}}^1$
. This answers a question posed by Ellenberg.
${\mathbb {P}}^1$
. This answers a question posed by Ellenberg.
The proof of Theorem 2.1 uses the following theorem about elliptic curves.
Theorem 2.2 Let
![]() $F \in {\mathbb {Z}}[x,y]$
be a non-singular binary quartic form. Then there exists square-free
$F \in {\mathbb {Z}}[x,y]$
be a non-singular binary quartic form. Then there exists square-free
![]() $d \in {\mathbb {Z}}$
such that the curve
$d \in {\mathbb {Z}}$
such that the curve
has a rational point and such that its Jacobian has positive rank as an elliptic curve defined over
![]() ${\mathbb {Q}}$
.
${\mathbb {Q}}$
.
The proof of Theorem 2.2 is provided to us by Shnidman in [Reference Shnidman15], and we graciously acknowledge his assistance.
Combining these results gives the following uniform statement.
Corollary 2.3 Let
![]() $\mathfrak {X}$
be a smooth proper stacky curve defined over
$\mathfrak {X}$
be a smooth proper stacky curve defined over
![]() ${\mathbb {Q}}$
such that
${\mathbb {Q}}$
such that
![]() $\mathfrak {X}$
has coarse space
$\mathfrak {X}$
has coarse space
![]() ${\mathbb {P}}^1_{\mathbb {Q}}$
or
${\mathbb {P}}^1_{\mathbb {Q}}$
or
![]() $\mathfrak {X}$
is a projective algebraic curve. Let
$\mathfrak {X}$
is a projective algebraic curve. Let
![]() $H_{\mathfrak {X}}$
be the height associated with the anti-canonical divisor
$H_{\mathfrak {X}}$
be the height associated with the anti-canonical divisor
![]() $-K_{\mathfrak {X}}$
. Then
$-K_{\mathfrak {X}}$
. Then
![]() $\chi (\mathfrak {X})>0$
if and only if
$\chi (\mathfrak {X})>0$
if and only if
![]() $H_{\mathfrak {X}}$
has the strong Northcott property.
$H_{\mathfrak {X}}$
has the strong Northcott property.
Proof If
![]() $\mathfrak {X}$
is an algebraic stack and not an algebraic curve, then it is of the form
$\mathfrak {X}$
is an algebraic stack and not an algebraic curve, then it is of the form
![]() $\mathfrak {X}=\mathfrak {X}({\mathbb {P}}^1_{\mathbb {Q}};({\mathbf {a}},{\mathbf {m}}))$
and (2.1) gives the desired result. On the other hand, if
$\mathfrak {X}=\mathfrak {X}({\mathbb {P}}^1_{\mathbb {Q}};({\mathbf {a}},{\mathbf {m}}))$
and (2.1) gives the desired result. On the other hand, if
![]() $\mathfrak {X}$
is a smooth projective and geometrically integral curve, then
$\mathfrak {X}$
is a smooth projective and geometrically integral curve, then
![]() $\chi (\mathfrak {X})\leq 0$
implies that
$\chi (\mathfrak {X})\leq 0$
implies that
![]() $-H_{C}$
does not have the Northcott property.
$-H_{C}$
does not have the Northcott property.
In cases where we can prove that the Northcott property fails, we expect, according to [Reference Ellenberg, Satriano and Zureick-Brown6], that there should be a stacky Vojta conjecture. In particular, we would like to know whether the anti-canonical height
![]() $\mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})}$
can be modified to recover the Northcott property. Difficulties arise because the ESZ-B height machine is not functorial in the usual sense; in the setting of algebraic varieties, one can work with a linear spaces of divisors and then apply the height machine which by functoriality will respect the linear structure. Such methods are not immediately available to us. Instead, we will apply the height machine, and then apply linear operations. We ask that for
$\mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})}$
can be modified to recover the Northcott property. Difficulties arise because the ESZ-B height machine is not functorial in the usual sense; in the setting of algebraic varieties, one can work with a linear spaces of divisors and then apply the height machine which by functoriality will respect the linear structure. Such methods are not immediately available to us. Instead, we will apply the height machine, and then apply linear operations. We ask that for
![]() $\mathfrak {X}=\mathfrak {X}({\mathbb {P}}^1:({\mathbf {a}},{\mathbf {m}}))$
with
$\mathfrak {X}=\mathfrak {X}({\mathbb {P}}^1:({\mathbf {a}},{\mathbf {m}}))$
with
![]() $\chi (\mathfrak {X})\leq 0$
, what can be said about the quantity
$\chi (\mathfrak {X})\leq 0$
, what can be said about the quantity
Clearly, if we change the exponent in the classical part of the height so that it is positive, then we will recover the Northcott property. In fact, we expect that something far less drastic suffices.
For a real number
![]() $\delta $
and the curve
$\delta $
and the curve
![]() $\mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}, {\mathbf {m}}))$
, define the height
$\mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}, {\mathbf {m}}))$
, define the height
 $$ \begin{align} \mathcal{H}_{({\mathbf{a}}, {\mathbf{m}})}^\delta(x,y) = \prod_{i=1}^n \phi_{m_i}(\ell_i(x,y))^{1/m_i} \max\{|x|, |y|\}^{\delta}. \end{align} $$
$$ \begin{align} \mathcal{H}_{({\mathbf{a}}, {\mathbf{m}})}^\delta(x,y) = \prod_{i=1}^n \phi_{m_i}(\ell_i(x,y))^{1/m_i} \max\{|x|, |y|\}^{\delta}. \end{align} $$
We then see that
![]() $\mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})} = \mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})}^{\chi (\mathfrak {X})}$
. Next, put
$\mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})} = \mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})}^{\chi (\mathfrak {X})}$
. Next, put
In fact,
![]() $\gamma (\mathfrak {X})$
depends only on
$\gamma (\mathfrak {X})$
depends only on
![]() ${\mathbf {m}}$
, so we may also write it as
${\mathbf {m}}$
, so we may also write it as
![]() $\gamma ({\mathbf {m}})$
. We make the following conjecture.
$\gamma ({\mathbf {m}})$
. We make the following conjecture.
Conjecture 2.4 (Northcott conjecture for stacky curves with coarse space
 ${\mathbb {P}}^1$
)
${\mathbb {P}}^1$
)
For all
![]() $\mathfrak {X}=\mathfrak {X}({\mathbb {P}}^1:({\mathbf {a}}, {\mathbf {m}}))$
, we have
$\mathfrak {X}=\mathfrak {X}({\mathbb {P}}^1:({\mathbf {a}}, {\mathbf {m}}))$
, we have
![]() $\gamma (\mathfrak {X}) = \min \{\chi (\mathfrak {X}), 0\}$
.
$\gamma (\mathfrak {X}) = \min \{\chi (\mathfrak {X}), 0\}$
.
Conjecture 2.4 is in fact a version of Vojta’s conjecture for stacky curves, and agrees with a conjecture of Ellenberg, Satriano, and Zureick-Brown in [Reference Ellenberg, Satriano and Zureick-Brown6]. Toward this conjecture, we have the following.
Theorem 2.5 We have
![]() $\gamma (\mathfrak {X}) = 0$
if
$\gamma (\mathfrak {X}) = 0$
if
![]() $\chi (\mathfrak {X}) \geq 0$
. Moreover, the height
$\chi (\mathfrak {X}) \geq 0$
. Moreover, the height
![]() $\mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})}^0$
has the Northcott property if and only if
$\mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})}^0$
has the Northcott property if and only if
![]() $\chi (\mathfrak {X})< 0$
.
$\chi (\mathfrak {X})< 0$
.
Combined with Theorem 2.1, the conjecture predicts that the set of
![]() $\delta \in {\mathbb {R}}$
such that
$\delta \in {\mathbb {R}}$
such that
![]() $\mathcal {H}^\delta _{{\mathbf {a}},{\mathbf {m}}}$
has the Northcott property is an interval of the form
$\mathcal {H}^\delta _{{\mathbf {a}},{\mathbf {m}}}$
has the Northcott property is an interval of the form
![]() $(\chi (\mathfrak {X}),\infty )$
when
$(\chi (\mathfrak {X}),\infty )$
when
![]() $\chi (\mathfrak {X})<0$
and
$\chi (\mathfrak {X})<0$
and
![]() $(0,\infty )$
when
$(0,\infty )$
when
![]() $\chi (\mathfrak {X})\geq 0$
. Therefore, while Theorem 2.1 tells us we cannot count points with
$\chi (\mathfrak {X})\geq 0$
. Therefore, while Theorem 2.1 tells us we cannot count points with
![]() $\mathcal {H}_{{\mathbf {a}},{\mathbf {m}}}$
, Conjecture 2.4 predicts that we can count points using
$\mathcal {H}_{{\mathbf {a}},{\mathbf {m}}}$
, Conjecture 2.4 predicts that we can count points using
![]() $\mathcal {H}^{\chi (\mathfrak {X})+\varepsilon }_{{\mathbf {a}},{\mathbf {m}}}$
for any
$\mathcal {H}^{\chi (\mathfrak {X})+\varepsilon }_{{\mathbf {a}},{\mathbf {m}}}$
for any
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Next, we prove that Conjecture 2.4 is a consequence of the
![]() $abc$
-conjecture. However, it seems that we are very far from being able to prove such a result as strong as Conjecture 2.4 unconditionally.
$abc$
-conjecture. However, it seems that we are very far from being able to prove such a result as strong as Conjecture 2.4 unconditionally.
Theorem 2.6 Suppose that the
![]() $abc$
-conjecture holds. Then, for any
$abc$
-conjecture holds. Then, for any
![]() $\delta> \delta ({\mathbf {m}})$
, the function
$\delta> \delta ({\mathbf {m}})$
, the function
![]() $\mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})}^{\delta } (x,y)$
on
$\mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})}^{\delta } (x,y)$
on
![]() $\mathfrak {X}({\mathbb {P}}^1: ({\mathbf {a}}, {\mathbf {m}}))$
has Northcott’s property.
$\mathfrak {X}({\mathbb {P}}^1: ({\mathbf {a}}, {\mathbf {m}}))$
has Northcott’s property.
In fact, Conjecture 2.4 is equivalent to the
![]() $abc$
-conjecture (see Theorem 1.3). The proof of the converse is quite different and so we give it in a separate subsection.
$abc$
-conjecture (see Theorem 1.3). The proof of the converse is quite different and so we give it in a separate subsection.
2.3 Quantitative arithmetic on stacky curves
In the positive Euler characteristic case, we consider a particular family of stacky curves, which includes an important example suggested by J. EllenbergFootnote 1 and show that our theory of heights matches [Reference Ellenberg, Satriano and Zureick-Brown6] in this instance. Finally, we verify a specific instance of the main conjecture in [Reference Ellenberg, Satriano and Zureick-Brown6] given by Ellenberg, Satriano, and Zureick-BrownFootnote 1 using analytical methods. We remark that P. Le Boudec had obtained the same result as us in independent work (private communication).
We study the expression (2.3) a bit more carefully. It is easy to deduce that
![]() $\delta ({\mathbf {m}}) \geq 0$
if and only if
$\delta ({\mathbf {m}}) \geq 0$
if and only if
![]() $n \leq 4$
, and
$n \leq 4$
, and
![]() $\delta ({\mathbf {m}})> 0$
only if
$\delta ({\mathbf {m}})> 0$
only if
![]() $n \leq 3$
. We will not consider the case
$n \leq 3$
. We will not consider the case
![]() $n \leq 2$
in this paper.
$n \leq 2$
in this paper.
If we assume
![]() $m_1 \leq m_2 \leq m_3$
, then the only cases when we have positive Euler characteristic are when
$m_1 \leq m_2 \leq m_3$
, then the only cases when we have positive Euler characteristic are when
![]() $m_1 = m_2 = 2$
,
$m_1 = m_2 = 2$
,
![]() $m_1 = 2, m_2 = m_3 = 3$
or
$m_1 = 2, m_2 = m_3 = 3$
or
![]() $m_1 = 2, m_2 = 3, m_3 = 4$
. In each of these three cases, the Northcott property for
$m_1 = 2, m_2 = 3, m_3 = 4$
. In each of these three cases, the Northcott property for
![]() $\mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})}$
holds trivially.
$\mathcal {H}_{({\mathbf {a}}, {\mathbf {m}})}$
holds trivially.
We now focus on the simplest cases, where
![]() $m_1 = m_2 = 2$
and
$m_1 = m_2 = 2$
and
![]() $m_3 = m, m \geq 2$
. Using that
$m_3 = m, m \geq 2$
. Using that
![]() $\operatorname {PGL}_2$
acts 3-transitively on
$\operatorname {PGL}_2$
acts 3-transitively on
![]() ${\mathbb {P}}^1$
, we reduce to the case
${\mathbb {P}}^1$
, we reduce to the case
![]() $\{a_1, a_2, a_3\} = \{0,-1,\infty \}$
. For
$\{a_1, a_2, a_3\} = \{0,-1,\infty \}$
. For
![]() $[x,y] \in {\mathbb {P}}^1$
, we may then set
$[x,y] \in {\mathbb {P}}^1$
, we may then set
with
![]() $x_1, y_1$
square-free, and
$x_1, y_1$
square-free, and
with
![]() $z_1, \ldots , z_{m-1}$
square-free. In this notation, the E-S-ZB height is given by
$z_1, \ldots , z_{m-1}$
square-free. In this notation, the E-S-ZB height is given by
We normalize the height so that the exponent of the “classical part” is equal to one, to obtain the normalized height
We now put
 $$ \begin{align} N_m(T) &= \# \{(x_1, x_2), (y_1, y_2), (z_1, \ldots, z_m) : \gcd(x_1 y_1, x_2 y_2)\nonumber\\& \qquad = 1, x_1, y_1, z_1, \ldots, z_{m-1} \text{ square-free and pairwise co-prime}, \end{align} $$
$$ \begin{align} N_m(T) &= \# \{(x_1, x_2), (y_1, y_2), (z_1, \ldots, z_m) : \gcd(x_1 y_1, x_2 y_2)\nonumber\\& \qquad = 1, x_1, y_1, z_1, \ldots, z_{m-1} \text{ square-free and pairwise co-prime}, \end{align} $$
We prove the following theorem, which gives a crude upper bound for
![]() $N_m(T)$
.
$N_m(T)$
.
Theorem 2.7 Let
![]() $\mathfrak {X} = \mathfrak {X}({\mathbb {P}}^1 : (0,2), (\infty , 2), (-1, m))$
, and let
$\mathfrak {X} = \mathfrak {X}({\mathbb {P}}^1 : (0,2), (\infty , 2), (-1, m))$
, and let
![]() $H_m$
be the height function on
$H_m$
be the height function on
![]() $\mathfrak {X}$
defined by (2.8). Then, for any
$\mathfrak {X}$
defined by (2.8). Then, for any
![]() $\varepsilon> 0$
, we have
$\varepsilon> 0$
, we have
When
![]() $m = 2$
, the upper bound of Theorem 2.7 is essentially the trivial bound, but it is nontrivial as soon as
$m = 2$
, the upper bound of Theorem 2.7 is essentially the trivial bound, but it is nontrivial as soon as
![]() $m> 2$
. In general, we expect the exponent in Theorem 2.7 to be equal to the lower bound. Indeed, this can be verified when
$m> 2$
. In general, we expect the exponent in Theorem 2.7 to be equal to the lower bound. Indeed, this can be verified when
![]() $m = 2$
. Even more, we can give an exact order of magnitude for
$m = 2$
. Even more, we can give an exact order of magnitude for
![]() $N_2(T)$
$N_2(T)$
Theorem 2.8 There exist positive numbers
![]() $c_1, c_2, c_3$
such that
$c_1, c_2, c_3$
such that
for all
![]() $T> c_3$
.
$T> c_3$
.
In particular, we confirm the stacky Batyrev–Manin conjecture [Reference Ellenberg, Satriano and Zureick-Brown6, Main Conjecture] for
![]() $\mathfrak {X}({\mathbb {P}}^1_{\mathbb {Q}},(a,2),(b,2),(c,2))$
. For this stacky curve, [Reference Ellenberg, Satriano and Zureick-Brown6, Main Conjecture] predicts that
$\mathfrak {X}({\mathbb {P}}^1_{\mathbb {Q}},(a,2),(b,2),(c,2))$
. For this stacky curve, [Reference Ellenberg, Satriano and Zureick-Brown6, Main Conjecture] predicts that
![]() $N_2(T) = O_{\varepsilon } \left (T^{1/2 + \varepsilon }\right )$
.Footnote
1
Our theorem gives an exact order of magnitude for
$N_2(T) = O_{\varepsilon } \left (T^{1/2 + \varepsilon }\right )$
.Footnote
1
Our theorem gives an exact order of magnitude for
![]() $N_2(T)$
. We remark, once again, that P. Le Boudec had obtained the same result. Further, our counting arguments are similar to those obtained by Le Boudec in [Reference le Boudec13] which studies the equation (7.4).
$N_2(T)$
. We remark, once again, that P. Le Boudec had obtained the same result. Further, our counting arguments are similar to those obtained by Le Boudec in [Reference le Boudec13] which studies the equation (7.4).
The other cases with positive Euler characteristic do not yield to the simple analytic counting arguments used to prove Theorem 2.8, though in principle counting rational points by height is a well-posed problem. We plan on returning to this issue in the future.
We illustrate how the stacky curve height machine (equation (2.2)) allows one to detect integral points on stacky curves. In this case, the standard height is given by
![]() $H_s(a,b) = \max \{|a|,|b|\}$
and the stacky height is given by (2.7). They are equal precisely when
$H_s(a,b) = \max \{|a|,|b|\}$
and the stacky height is given by (2.7). They are equal precisely when
or in the notation of (7.4), that
![]() $|x_1| = |x_2| = |x_3| = 1$
. (7.4) then turns into
$|x_1| = |x_2| = |x_3| = 1$
. (7.4) then turns into
and up to rearranging we are essentially counting points on the conic
Therefore, if we denote by
![]() ${\mathcal {N}}(T)$
the number of integral points (in the sense of Definition 3.19) on
${\mathcal {N}}(T)$
the number of integral points (in the sense of Definition 3.19) on
![]() ${\mathbb {P}}_{2,2,2}^1$
, then:
${\mathbb {P}}_{2,2,2}^1$
, then:
Corollary 2.9 There exist positive numbers
![]() $c_1, c_2, c_3$
such that for all
$c_1, c_2, c_3$
such that for all
![]() $T> c_3$
we have
$T> c_3$
we have
The proof is elementary, since the curve can be explicitly parametrized by
The condition
![]() $\max \{|y_1|, |y_2\} \leq T^{1/2}$
is subsumed by
$\max \{|y_1|, |y_2\} \leq T^{1/2}$
is subsumed by
![]() $u^2 + v^2 \leq 4T^{1/2}$
say, so the number of possible
$u^2 + v^2 \leq 4T^{1/2}$
say, so the number of possible
![]() $u,v$
’s is
$u,v$
’s is
![]() $\asymp T^{1/2}$
as desired.
$\asymp T^{1/2}$
as desired.
Theorem 2.8 and Corollary 2.9 imply that asymptotically
![]() $0\%$
of the rational points on
$0\%$
of the rational points on
![]() $\mathfrak {X}({\mathbb {P}}^1 :(0,2),,(-1,2),(\infty ,2))({\mathbb {Q}})$
are integral, in the sense of Darmon (Definition 3.19).
$\mathfrak {X}({\mathbb {P}}^1 :(0,2),,(-1,2),(\infty ,2))({\mathbb {Q}})$
are integral, in the sense of Darmon (Definition 3.19).
To close off this subsection, we note that in [Reference Bhargava and Poonen2], Bhargava and Poonen study situations where the rational and integral points of a stacky curve satisfy the Hasse Principle. Motivated by this work, we prove that the integral points on
![]() $\mathfrak {X}({\mathbb {P}}^1 : (a_1, 2), \ldots , (a_n, 2))$
satisfy Hasse’s principle.
$\mathfrak {X}({\mathbb {P}}^1 : (a_1, 2), \ldots , (a_n, 2))$
satisfy Hasse’s principle.
Theorem 2.10 Let
Then
![]() $\mathfrak {X}$
has integral points if and only if the ternary quadratic form
$\mathfrak {X}$
has integral points if and only if the ternary quadratic form
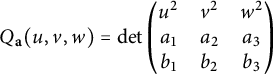 $$\begin{align*}Q_{\mathbf{a}}(u,v,w) = \det \begin{pmatrix} u^2 & v^2 & w^2 \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{pmatrix} \end{align*}$$
$$\begin{align*}Q_{\mathbf{a}}(u,v,w) = \det \begin{pmatrix} u^2 & v^2 & w^2 \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{pmatrix} \end{align*}$$
defines a conic with a rational point.
Notation
We denote by
![]() $d_k(n)$
for the number of ways of writing n as a product of k (not necessarily distinct) positive integers, and write
$d_k(n)$
for the number of ways of writing n as a product of k (not necessarily distinct) positive integers, and write
![]() $d(n) = d_2(n)$
for the usual divisor function. We will also use the big-O notation as well as Landau’s notation. In particular, we will denote in the subscripts any dependencies; if there are no subscripts, then the implied constants are absolute.
$d(n) = d_2(n)$
for the usual divisor function. We will also use the big-O notation as well as Landau’s notation. In particular, we will denote in the subscripts any dependencies; if there are no subscripts, then the implied constants are absolute.
3 (Stacky) Heights on stacky curves
In this section, we give an alternative construction of the height functions constructed in [Reference Ellenberg, Satriano and Zureick-Brown6] in a special case: We construct the ESZ-B heights associated with line bundles on stacky curves with coarse space
![]() ${\mathbb {P}}^1_{\mathbb {Q}}$
. We use [Reference Voight and Zureick-Brown20] as our main reference, though we made substantial use of [16].
${\mathbb {P}}^1_{\mathbb {Q}}$
. We use [Reference Voight and Zureick-Brown20] as our main reference, though we made substantial use of [16].
Definition 3.1 (Definition 5.2.1 in [Reference Voight and Zureick-Brown20])
A stacky curve
![]() $\mathfrak {X}$
over a field k of characteristic 0 is a smooth proper geometrically connected Deligne–Mumford stack over k of dimension 1 that contains an open dense subscheme.
$\mathfrak {X}$
over a field k of characteristic 0 is a smooth proper geometrically connected Deligne–Mumford stack over k of dimension 1 that contains an open dense subscheme.
A stacky curve can be thought of a smooth projective curve, along with a finite choice of points with integer multiplicities.
Theorem 3.2 (Classification of nice stacky curves: Lemma 5.3.10 in [Reference Voight and Zureick-Brown20])
Let
![]() $\mathfrak {X}$
be a stacky curve over k. Then the isomorphism class of
$\mathfrak {X}$
be a stacky curve over k. Then the isomorphism class of
![]() $\mathfrak {X}$
is determined by the coarse moduli space X of
$\mathfrak {X}$
is determined by the coarse moduli space X of
![]() $\mathfrak {X}$
and the orders of the stabilizer groups of points of
$\mathfrak {X}$
and the orders of the stabilizer groups of points of
![]() $\mathfrak {X}$
.
$\mathfrak {X}$
.
Before continuing, let us fix some notation. We let
![]() $\mathfrak {X}=(X:(P_1,m_1), \ldots , (P_r,m_r))$
be the stacky curve with coarse space X and a
$\mathfrak {X}=(X:(P_1,m_1), \ldots , (P_r,m_r))$
be the stacky curve with coarse space X and a
![]() $\mu _{m_i}$
stabilizer at
$\mu _{m_i}$
stabilizer at
![]() $P_i$
. In light of Theorem 3.2, this determines a unique stacky curve.
$P_i$
. In light of Theorem 3.2, this determines a unique stacky curve.
3.1 Construction of heights
We will give an alternative construction of heights on a stacky curve associated with line bundles. Our construction only depends on the coarse space, and the multiplicities of points. The ideas exposited in this section can be viewed as a “bottom up” construction, similar to the work of Geraschenko and Satriano in [Reference Geraschenko and Satriano10]. We then show that our height construction corresponds to the heights associated with line bundles in [Reference Ellenberg, Satriano and Zureick-Brown6] when the coarse space is
![]() ${\mathbb {P}}^1_{\mathbb {Q}}$
. As in the classical setting, we will work with height functions up to some bounded function. Line bundles on a stacky curve can be described as follows.
${\mathbb {P}}^1_{\mathbb {Q}}$
. As in the classical setting, we will work with height functions up to some bounded function. Line bundles on a stacky curve can be described as follows.
Lemma 3.3 ([Reference Fantechi, Mann and Nironi7, Section 1.3])
Let
![]() $\mathfrak {X}=\mathfrak {X}(X:(P_1,\cdots ,P_r),(m_1,\cdots ,m_r))$
. Let
$\mathfrak {X}=\mathfrak {X}(X:(P_1,\cdots ,P_r),(m_1,\cdots ,m_r))$
. Let
![]() ${\mathcal {O}}_{X}(P)$
be the line bundle associated with the divisor P on X. Then there are line bundles
${\mathcal {O}}_{X}(P)$
be the line bundle associated with the divisor P on X. Then there are line bundles
![]() ${\mathcal {L}}_{P_i}$
on
${\mathcal {L}}_{P_i}$
on
![]() $\mathfrak {X}$
such that
$\mathfrak {X}$
such that
where
![]() $\pi _{\mathfrak {X}}\colon \mathfrak {X}\rightarrow X$
is the coarse space map. Moreover, we have that any line bundle
$\pi _{\mathfrak {X}}\colon \mathfrak {X}\rightarrow X$
is the coarse space map. Moreover, we have that any line bundle
![]() ${\mathcal {L}}$
on
${\mathcal {L}}$
on
![]() $\mathfrak {X}$
can be uniquely written as
$\mathfrak {X}$
can be uniquely written as
 $$ \begin{align} {\mathcal{L}}\cong \pi_{\mathfrak{X}}^*M\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i}, \end{align} $$
$$ \begin{align} {\mathcal{L}}\cong \pi_{\mathfrak{X}}^*M\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i}, \end{align} $$
where
![]() $0\leq d_i<m_i$
and M is a line bundle on X.
$0\leq d_i<m_i$
and M is a line bundle on X.
We will use the definition of the degree of a line bundle on a stacky curve.
Definition 3.4 Let
![]() $\mathfrak {X}=\mathfrak {X}(X:(P_1,\ldots ,P_r),(m_1, \ldots , m_r)))$
and
$\mathfrak {X}=\mathfrak {X}(X:(P_1,\ldots ,P_r),(m_1, \ldots , m_r)))$
and
![]() $\mathcal {L}=\pi _{\mathfrak {X}}^* D\otimes \prod _{i=1}^r{\mathcal {L}}_{P_i}^{\otimes d_i}$
. Then we define
$\mathcal {L}=\pi _{\mathfrak {X}}^* D\otimes \prod _{i=1}^r{\mathcal {L}}_{P_i}^{\otimes d_i}$
. Then we define
 $$\begin{align*}\deg_{\mathfrak{X}} \mathcal{{\mathcal{L}}}=\deg_X D+\sum_{i=1}^r\dfrac{d_i}{m_i}.\end{align*}$$
$$\begin{align*}\deg_{\mathfrak{X}} \mathcal{{\mathcal{L}}}=\deg_X D+\sum_{i=1}^r\dfrac{d_i}{m_i}.\end{align*}$$
In [Reference Ellenberg, Satriano and Zureick-Brown6], the height is broken down into two parts: a so-called stable part and a local part. We now define the stable part in our setting.
Definition 3.5 Let
![]() $\mathfrak {X}=\mathfrak {X}(X:(P_1,\ldots ,P_r),(m_1, \ldots , m_r)))$
, and let
$\mathfrak {X}=\mathfrak {X}(X:(P_1,\ldots ,P_r),(m_1, \ldots , m_r)))$
, and let
![]() ${\mathcal {L}}$
be a line bundle on
${\mathcal {L}}$
be a line bundle on
![]() $\mathfrak {X}$
with
$\mathfrak {X}$
with
 $$\begin{align*}{\mathcal{L}}\cong \pi_{\mathfrak{X}}^*M\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i},\end{align*}$$
$$\begin{align*}{\mathcal{L}}\cong \pi_{\mathfrak{X}}^*M\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i},\end{align*}$$
where
![]() $0\leq d_i<m_i$
and M is a line bundle on X with
$0\leq d_i<m_i$
and M is a line bundle on X with
![]() $\pi _{\mathfrak {X}}$
being the coarse space map. We define the stable height associated with
$\pi _{\mathfrak {X}}$
being the coarse space map. We define the stable height associated with
![]() ${\mathcal {L}}$
as
${\mathcal {L}}$
as
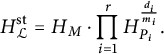 $$\begin{align*}H_{{\mathcal{L}}}^{\mathrm{st}}=H_M\cdot\prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}.\end{align*}$$
$$\begin{align*}H_{{\mathcal{L}}}^{\mathrm{st}}=H_M\cdot\prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}.\end{align*}$$
Later in Proposition 4.3, we show that this definition matches the one given in [Reference Ellenberg, Satriano and Zureick-Brown6]. The stable height should be thought of as the part of the height consisting of classical height functions.
We will use the notions introduced in Section 3 to define our heights. We further choose a finite set of primes S of
![]() ${\mathcal {O}}_K$
containing all the primes of bad reduction and all infinite places of K. We further choose a smooth and proper model
${\mathcal {O}}_K$
containing all the primes of bad reduction and all infinite places of K. We further choose a smooth and proper model
![]() $\underline {X}$
of X over
$\underline {X}$
of X over
![]() ${\mathcal {O}}_{K,S}$
. Let
${\mathcal {O}}_{K,S}$
. Let
![]() $P,Q$
be distinct points in
$P,Q$
be distinct points in
![]() $X(K)$
and place
$X(K)$
and place
![]() $\nu $
a place in K with
$\nu $
a place in K with
![]() $\nu \notin S$
. Take
$\nu \notin S$
. Take
![]() $\mathfrak {p}_\nu \subset {\mathcal {O}}_K$
to be the prime ideal associated with
$\mathfrak {p}_\nu \subset {\mathcal {O}}_K$
to be the prime ideal associated with
![]() $\nu $
.
$\nu $
.
Definition 3.6 (Darmon [Reference Darmon4])
We define the intersection multiplicity of P and Q at
![]() $\nu $
as follows:
$\nu $
as follows:
where the maximum over the empty set is defined to be 0.
We now package all the intersection multiplicities together while taking into account the arithmetic of the field extension
![]() $K\mid {\mathbb {Q}}$
. We shall use the following notation for the remainder of this section.
$K\mid {\mathbb {Q}}$
. We shall use the following notation for the remainder of this section.
Notation 3.7 Fix a stacky curve
![]() $\mathfrak {X}=(X:(P_1,m_1), \ldots , (P_r,m_r))$
defined over a number field K. Choose a finite set of primes S of
$\mathfrak {X}=(X:(P_1,m_1), \ldots , (P_r,m_r))$
defined over a number field K. Choose a finite set of primes S of
![]() ${\mathcal {O}}_K$
containing all the primes of bad reduction and all infinite places of K. We further choose a smooth and proper model
${\mathcal {O}}_K$
containing all the primes of bad reduction and all infinite places of K. We further choose a smooth and proper model
![]() $\underline {X}$
of X over
$\underline {X}$
of X over
![]() ${\mathcal {O}}_{K,S}$
. We define the following quantities.
${\mathcal {O}}_{K,S}$
. We define the following quantities.
-
(1) Given a prime
 $\mathfrak {p}_\nu \subseteq {\mathcal {O}}_{K}$
, we let
$\mathfrak {p}_\nu \subseteq {\mathcal {O}}_{K}$
, we let
 $\mathfrak {f}_\nu =[{\mathcal {O}}_K/\mathfrak {p}_\nu \colon {\mathbb {Z}}/(\mathfrak {p}_\nu \cap {\mathbb {Z}})].$
$\mathfrak {f}_\nu =[{\mathcal {O}}_K/\mathfrak {p}_\nu \colon {\mathbb {Z}}/(\mathfrak {p}_\nu \cap {\mathbb {Z}})].$
-
(2) Fix
 $P\in X(K)$
,
$P\in X(K)$
,
 $t\in X(K)\setminus \{P\}$
and
$t\in X(K)\setminus \{P\}$
and
 $\nu \notin S$
, now put
$\nu \notin S$
, now put
 $(t\cdot P)_p=\sum _{\nu \notin S,\nu \mid p}\mathfrak {f}_\nu \cdot (t\cdot P)_\nu $
.
$(t\cdot P)_p=\sum _{\nu \notin S,\nu \mid p}\mathfrak {f}_\nu \cdot (t\cdot P)_\nu $
. -
(3) We set
and $$ \begin{align*} \lambda_{S,\underline{X},\nu}(P,t)=\lambda_{\nu}(P,t)=\mathrm{N}(\mathfrak{p}_\nu)^{(t\cdot P)_\nu} \end{align*} $$
$$ \begin{align*} \lambda_{S,\underline{X},\nu}(P,t)=\lambda_{\nu}(P,t)=\mathrm{N}(\mathfrak{p}_\nu)^{(t\cdot P)_\nu} \end{align*} $$
 $$ \begin{align*} \lambda_{S,\underline{X}}(P,t) = \lambda(P,t)=\prod_{\nu\notin S}\lambda_\nu(P,t)=\prod_pp^{(t\cdot P)_p}. \end{align*} $$
$$ \begin{align*} \lambda_{S,\underline{X}}(P,t) = \lambda(P,t)=\prod_{\nu\notin S}\lambda_\nu(P,t)=\prod_pp^{(t\cdot P)_p}. \end{align*} $$
The integer
![]() $\lambda (P,t)$
is an exponential version of the familiar looking intersection product
$\lambda (P,t)$
is an exponential version of the familiar looking intersection product
 $$ \begin{align*} \sum_{\nu\notin S}(t\cdot P)_\nu \log(p)=\sum_{p}\left(\sum_{\nu\notin S,\nu \mid p}\mathfrak{f}_\nu\cdot (t\cdot P)_\nu\log(p)\right)=\sum_p(t\cdot P)_p\log (p). \end{align*} $$
$$ \begin{align*} \sum_{\nu\notin S}(t\cdot P)_\nu \log(p)=\sum_{p}\left(\sum_{\nu\notin S,\nu \mid p}\mathfrak{f}_\nu\cdot (t\cdot P)_\nu\log(p)\right)=\sum_p(t\cdot P)_p\log (p). \end{align*} $$
We will also require the following basic functions.
Definition 3.8 For each integer
![]() $m\geq 1$
, we let
$m\geq 1$
, we let
![]() $[0], \ldots ,[m-1]$
be a set of representatives of the equivalence classes of
$[0], \ldots ,[m-1]$
be a set of representatives of the equivalence classes of
![]() ${\mathbb {Z}}/m{\mathbb {Z}}$
. Define
${\mathbb {Z}}/m{\mathbb {Z}}$
. Define
for
![]() $0\leq r<m$
and
$0\leq r<m$
and
for any
![]() $d\in {\mathbb {Z}}$
. With this notation,
$d\in {\mathbb {Z}}$
. With this notation,
![]() $N_{m,-}=N_{m,1}$
.
$N_{m,-}=N_{m,1}$
.
These functions are used to make the following definition of the height function associated with
![]() ${\mathcal {L}}_{P_i}^{d_i}$
.
${\mathcal {L}}_{P_i}^{d_i}$
.
Definition 3.9 The stacky height function associated with
![]() ${\mathcal {L}}_{P_i}^{d_i}$
is a function
${\mathcal {L}}_{P_i}^{d_i}$
is a function
defined by
 $$ \begin{align} H_{{\mathcal{L}}_{P_i}^{d_i}}(t)=\left(\prod_p p^{N_{m_i,d_i}((t\cdot P_i)_p)}\right)^{\frac{1}{m_i}},\end{align} $$
$$ \begin{align} H_{{\mathcal{L}}_{P_i}^{d_i}}(t)=\left(\prod_p p^{N_{m_i,d_i}((t\cdot P_i)_p)}\right)^{\frac{1}{m_i}},\end{align} $$
where
![]() $N_{m_i,d_i}\colon {\mathbb {Z}}_{\geq 0}\rightarrow {\mathbb {Z}}_{\geq 0}$
is the function defined by equation (3.4).
$N_{m_i,d_i}\colon {\mathbb {Z}}_{\geq 0}\rightarrow {\mathbb {Z}}_{\geq 0}$
is the function defined by equation (3.4).
Putting this all together, we obtain the following.
Definition 3.10 (Definition of heights)
Let
![]() ${\mathcal {L}}$
be the line bundle
${\mathcal {L}}$
be the line bundle
![]() ${\mathcal {L}}\cong \pi _{\mathfrak {X}}^*M\otimes \prod _{i=1}^r{\mathcal {L}}_{P_i}^{\otimes d_i}$
on
${\mathcal {L}}\cong \pi _{\mathfrak {X}}^*M\otimes \prod _{i=1}^r{\mathcal {L}}_{P_i}^{\otimes d_i}$
on
![]() $\mathfrak {X}$
. The stacky height associated with
$\mathfrak {X}$
. The stacky height associated with
![]() ${\mathcal {L}}$
is defined to be
${\mathcal {L}}$
is defined to be
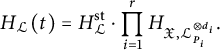 $$\begin{align*}H_{\mathcal{L}}(t)=H_{{\mathcal{L}}}^{\mathrm{st}}\cdot \prod_{i=1}^rH_{\mathfrak{X},{\mathcal{L}}_{P_i}^{\otimes d_i}}.\end{align*}$$
$$\begin{align*}H_{\mathcal{L}}(t)=H_{{\mathcal{L}}}^{\mathrm{st}}\cdot \prod_{i=1}^rH_{\mathfrak{X},{\mathcal{L}}_{P_i}^{\otimes d_i}}.\end{align*}$$
Unwinding the definitions, we obtain
 $$ \begin{align} H_{\mathcal{L}}(t)&=H_{{\mathcal{L}}}^{\mathrm{st}}\cdot \prod_{i=1}^rH_{\mathfrak{X},{\mathcal{L}}_{P_i}^{\otimes d_i}} \end{align} $$
$$ \begin{align} H_{\mathcal{L}}(t)&=H_{{\mathcal{L}}}^{\mathrm{st}}\cdot \prod_{i=1}^rH_{\mathfrak{X},{\mathcal{L}}_{P_i}^{\otimes d_i}} \end{align} $$
 $$ \begin{align} & =H_M\cdot \prod_{i=1}^r\left(H_{P_i}^{d_i}\cdot \prod_{p}p^{N_{m_i,d_i}((t\cdot P_i)_p)}\right)^{\frac{1}{m_i}} \end{align} $$
$$ \begin{align} & =H_M\cdot \prod_{i=1}^r\left(H_{P_i}^{d_i}\cdot \prod_{p}p^{N_{m_i,d_i}((t\cdot P_i)_p)}\right)^{\frac{1}{m_i}} \end{align} $$
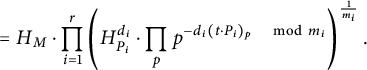 $$ \begin{align} & = H_M\cdot \prod_{i=1}^r\left(H_{P_i}^{d_i}\cdot \prod_{p}p^{-d_i(t\cdot P_i)_p \quad\mod m_i}\right)^{\frac{1}{m_i}}. \end{align} $$
$$ \begin{align} & = H_M\cdot \prod_{i=1}^r\left(H_{P_i}^{d_i}\cdot \prod_{p}p^{-d_i(t\cdot P_i)_p \quad\mod m_i}\right)^{\frac{1}{m_i}}. \end{align} $$
This decomposition allows us to define what we call the classical and stacky part of a height function.
Definition 3.11 We call
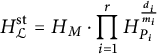 $$\begin{align*}H_{{\mathcal{L}}}^{\mathrm{st}}=H_M\cdot \prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}\end{align*}$$
$$\begin{align*}H_{{\mathcal{L}}}^{\mathrm{st}}=H_M\cdot \prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}\end{align*}$$
the classical part of the height
![]() $H_{\mathcal {L}}$
and
$H_{\mathcal {L}}$
and
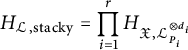 $$\begin{align*}H_{{\mathcal{L}},\mathrm{stacky}}=\prod_{i=1}^rH_{\mathfrak{X},{\mathcal{L}}_{P_i}^{\otimes d_i}}\end{align*}$$
$$\begin{align*}H_{{\mathcal{L}},\mathrm{stacky}}=\prod_{i=1}^rH_{\mathfrak{X},{\mathcal{L}}_{P_i}^{\otimes d_i}}\end{align*}$$
the stacky part of the height
![]() $H_{\mathcal {L}}$
.
$H_{\mathcal {L}}$
.
We will primarily work explicitly with stacky heights on
![]() ${\mathbb {P}}^1$
, the formulas in that case are as follows.
${\mathbb {P}}^1$
, the formulas in that case are as follows.
Corollary 3.12 Use the notation of Notation 3.7. The canonical height function may be computed as
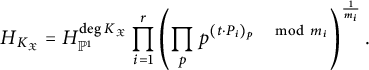 $$\begin{align*}H_{K_{\mathfrak{X}}}=H_{{\mathbb{P}}^1}^{\deg K_{\mathfrak{X}}}\prod_{i=1}^r\left(\prod_pp^{(t\cdot P_i)_p \quad\mod m_i}\right)^{\frac{1}{m_i}}.\end{align*}$$
$$\begin{align*}H_{K_{\mathfrak{X}}}=H_{{\mathbb{P}}^1}^{\deg K_{\mathfrak{X}}}\prod_{i=1}^r\left(\prod_pp^{(t\cdot P_i)_p \quad\mod m_i}\right)^{\frac{1}{m_i}}.\end{align*}$$
The anti-canonical height function may be computed as
 $$\begin{align*}H_{-K_{\mathfrak{X}}}=H_{{\mathbb{P}}^1}^{-\deg K_{\mathfrak{X}}}\prod_{i=1}^r\left(\prod_pp^{-(t\cdot P_i)_p \quad\mod m_i}\right)^{\frac{1}{m_i}}.\end{align*}$$
$$\begin{align*}H_{-K_{\mathfrak{X}}}=H_{{\mathbb{P}}^1}^{-\deg K_{\mathfrak{X}}}\prod_{i=1}^r\left(\prod_pp^{-(t\cdot P_i)_p \quad\mod m_i}\right)^{\frac{1}{m_i}}.\end{align*}$$
Proof This follows directly from the definition, Corollary 4.4, and the fact that
![]() $K_{\mathfrak {X}}$
corresponds to the line bundle
$K_{\mathfrak {X}}$
corresponds to the line bundle
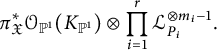 $$\begin{align*}\pi^*_{\mathfrak{X}} {\mathcal{O}}_{{\mathbb{P}}^1}(K_{{\mathbb{P}}^1})\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes m_i-1}.\\[-39pt] \end{align*}$$
$$\begin{align*}\pi^*_{\mathfrak{X}} {\mathcal{O}}_{{\mathbb{P}}^1}(K_{{\mathbb{P}}^1})\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes m_i-1}.\\[-39pt] \end{align*}$$
We now introduce two multiplicative functions
![]() $\phi _m$
and
$\phi _m$
and
![]() $r_m$
that depend on an integer
$r_m$
that depend on an integer
![]() $m\geq 1$
. The functions
$m\geq 1$
. The functions
![]() $\phi _m$
and
$\phi _m$
and
![]() $r_m$
are dual to one another in a certain sense. This duality is key to understanding the nonlinear aspects of heights on stacky curves.
$r_m$
are dual to one another in a certain sense. This duality is key to understanding the nonlinear aspects of heights on stacky curves.
Let x be a positive integer with prime factorization
![]() $x=\prod _{p}p^{\operatorname {ord}_p(x)}$
. We will work with the following functions.
$x=\prod _{p}p^{\operatorname {ord}_p(x)}$
. We will work with the following functions.
-
(1) Using the division algorithm, we define integers
 $q_{p,m}(x),r_{p,m}(x)$
by the equation
$q_{p,m}(x),r_{p,m}(x)$
by the equation
 $\operatorname {ord}_p(x)=q_{p,m}(x)m+r_{p,m}(x)$
where
$\operatorname {ord}_p(x)=q_{p,m}(x)m+r_{p,m}(x)$
where
 $0\leq r_{p,m}(x)<m$
.
$0\leq r_{p,m}(x)<m$
. -
(2)
 $q_m(x)=\prod _{p}p^{q_{p,m}(x)}$
and
$q_m(x)=\prod _{p}p^{q_{p,m}(x)}$
and
 $r_m(x)=\prod _{p}p^{r_{m,p}(x)}$
.
$r_m(x)=\prod _{p}p^{r_{m,p}(x)}$
. -
(3) Set
 $\phi _m(x)$
to be the least positive integer such that
$\phi _m(x)$
to be the least positive integer such that
 $x\phi _m(x)$
is an mth power.
$x\phi _m(x)$
is an mth power. -
(4) We define the m-radical of x to be the product of all prime divisors of x whose order is not a factor of m. In other words,
 $$\begin{align*}\operatorname{rad}_m(x)=\prod_{p\ \mathrm{s.t.}\ \operatorname{ord}_p(x)\neq 0 \quad\mod m}p.\end{align*}$$
$$\begin{align*}\operatorname{rad}_m(x)=\prod_{p\ \mathrm{s.t.}\ \operatorname{ord}_p(x)\neq 0 \quad\mod m}p.\end{align*}$$
The
![]() $r_m$
is related to
$r_m$
is related to
![]() $N_{m,\mathrm {can}}$
and
$N_{m,\mathrm {can}}$
and
![]() $\phi _m$
is related to
$\phi _m$
is related to
![]() $N_{m,-}$
because of the following.
$N_{m,-}$
because of the following.
Proposition 3.13 Let
![]() $x\in {\mathbb {Z}}_{\geq 0}$
. Then we have
$x\in {\mathbb {Z}}_{\geq 0}$
. Then we have
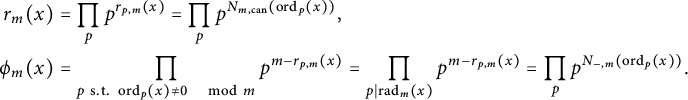 $$ \begin{align*} r_m(x)&=\prod_{p}p^{r_{p,m}(x)}=\prod_{p}p^{N_{m,\mathrm{can}}(\operatorname{ord}_p(x))},\\ \phi_m(x)&=\prod_{p\ \mathrm{s.t.}\ \operatorname{ord}_p(x)\neq 0 \quad\mod m}p^{m-r_{p,m}(x)}=\prod_{p\mid \operatorname{rad}_m(x)}p^{m-r_{p,m}(x)}=\prod_pp^{N_{-,m}(\operatorname{ord}_p(x))}. \end{align*} $$
$$ \begin{align*} r_m(x)&=\prod_{p}p^{r_{p,m}(x)}=\prod_{p}p^{N_{m,\mathrm{can}}(\operatorname{ord}_p(x))},\\ \phi_m(x)&=\prod_{p\ \mathrm{s.t.}\ \operatorname{ord}_p(x)\neq 0 \quad\mod m}p^{m-r_{p,m}(x)}=\prod_{p\mid \operatorname{rad}_m(x)}p^{m-r_{p,m}(x)}=\prod_pp^{N_{-,m}(\operatorname{ord}_p(x))}. \end{align*} $$
In particular, we have
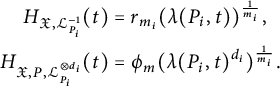 $$ \begin{align*} H_{\mathfrak{X},{\mathcal{L}}_{P_i}^{-1}}(t)&=r_{m_i}(\lambda(P_i,t))^{\frac{1}{m_i}},\\ H_{\mathfrak{X},P,{\mathcal{L}}_{P_i}^{\otimes d_i}}(t)&=\phi_m(\lambda(P_i,t)^{d_i})^{\frac{1}{m_i}}. \end{align*} $$
$$ \begin{align*} H_{\mathfrak{X},{\mathcal{L}}_{P_i}^{-1}}(t)&=r_{m_i}(\lambda(P_i,t))^{\frac{1}{m_i}},\\ H_{\mathfrak{X},P,{\mathcal{L}}_{P_i}^{\otimes d_i}}(t)&=\phi_m(\lambda(P_i,t)^{d_i})^{\frac{1}{m_i}}. \end{align*} $$
From the above formulas, we obtain the following.
Proposition 3.14 Fix and integer
![]() $m>1$
and let
$m>1$
and let
![]() $x\in {\mathbb {Z}}$
. Then:
$x\in {\mathbb {Z}}$
. Then:
-
(1) Both
 $r_m$
and
$r_m$
and
 $\phi _m$
are multiplicative functions.
$\phi _m$
are multiplicative functions. -
(2)
 $\phi _m(x)r_m(x)=\operatorname {rad}_m(x)^m$
.
$\phi _m(x)r_m(x)=\operatorname {rad}_m(x)^m$
. -
(3)
 $\phi _m(x)=1\iff r_m(x)=1$
.
$\phi _m(x)=1\iff r_m(x)=1$
. -
(4) If
 $m=2$
, then
$m=2$
, then
 $r_m(x)=\phi _m(x)$
.
$r_m(x)=\phi _m(x)$
.
With these definitions in hand, we relate our height functions on the stacky curve
![]() $\mathfrak {X}$
to a function from the functions
$\mathfrak {X}$
to a function from the functions
![]() $\phi _{m_P}(\lambda (P,t))^{\frac {1}{m_P}},$
and the classical Weil heights on the coarse space X.
$\phi _{m_P}(\lambda (P,t))^{\frac {1}{m_P}},$
and the classical Weil heights on the coarse space X.
Corollary 3.15 Use the notation of Notation 3.7. Consider the line bundle
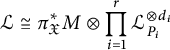 $$ \begin{align*} {\mathcal{L}}\cong \pi_{\mathfrak{X}}^*M\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i} \end{align*} $$
$$ \begin{align*} {\mathcal{L}}\cong \pi_{\mathfrak{X}}^*M\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i} \end{align*} $$
with
![]() $0\leq d_i\leq m_i-1$
. Then
$0\leq d_i\leq m_i-1$
. Then
 $$ \begin{align} H_{\mathcal{L}}=H_M\cdot \prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}\cdot \prod_{i=1}^r \phi_{m_i}(\lambda(P_i,t)^{d_i})^{\frac{1}{m_i}}. \end{align} $$
$$ \begin{align} H_{\mathcal{L}}=H_M\cdot \prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}\cdot \prod_{i=1}^r \phi_{m_i}(\lambda(P_i,t)^{d_i})^{\frac{1}{m_i}}. \end{align} $$
In particular, when
![]() $X={\mathbb {P}}^1$
, we have
$X={\mathbb {P}}^1$
, we have
 $$ \begin{align} H_{K_{\mathfrak{X}}}(t)&=H_{{\mathbb{P}}^1}^{-\chi(\mathfrak{X})}(t)\cdot\prod_{i=1}^rr_{m_i}(\lambda(P_i,t))^{\frac{1}{m_i}}, \end{align} $$
$$ \begin{align} H_{K_{\mathfrak{X}}}(t)&=H_{{\mathbb{P}}^1}^{-\chi(\mathfrak{X})}(t)\cdot\prod_{i=1}^rr_{m_i}(\lambda(P_i,t))^{\frac{1}{m_i}}, \end{align} $$
 $$ \begin{align} H_{-K_{\mathfrak{X}}}(t)&=H_{{\mathbb{P}}^1}^{\chi(\mathfrak{X})}(t)\cdot\prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t))^{\frac{1}{m_i}}, \end{align} $$
$$ \begin{align} H_{-K_{\mathfrak{X}}}(t)&=H_{{\mathbb{P}}^1}^{\chi(\mathfrak{X})}(t)\cdot\prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t))^{\frac{1}{m_i}}, \end{align} $$
where
![]() $\chi (\mathfrak {X})=-\deg K_{\mathfrak {X}} $
is the Euler characteristic of
$\chi (\mathfrak {X})=-\deg K_{\mathfrak {X}} $
is the Euler characteristic of
![]() $\mathfrak {X}$
.
$\mathfrak {X}$
.
One interesting feature of the heights given by (3.10) is that they differentiate between rational and integral points on stacky curves. The connection to [Reference Ellenberg, Satriano and Zureick-Brown6] and our heights is the following, which is proved in 4.1.
Theorem 3.16 Fix a stacky curve
![]() $\mathfrak {X}=({\mathbb {P}}^1_{\mathbb {Q}}:(P_1,m_1), \ldots , (P_r,m_r))$
. Choose S to be the set of all finite primes of
$\mathfrak {X}=({\mathbb {P}}^1_{\mathbb {Q}}:(P_1,m_1), \ldots , (P_r,m_r))$
. Choose S to be the set of all finite primes of
![]() ${\mathbb {Z}}$
, and let
${\mathbb {Z}}$
, and let
![]() ${\mathbb {P}}^1_{\mathbb {Z}}$
be the canonical model of
${\mathbb {P}}^1_{\mathbb {Z}}$
be the canonical model of
![]() ${\mathbb {P}}^1_{\mathbb {Q}}$
over
${\mathbb {P}}^1_{\mathbb {Q}}$
over
![]() ${\mathbb {Z}}$
. Let
${\mathbb {Z}}$
. Let
![]() ${\mathcal {L}}$
be a line bundle on
${\mathcal {L}}$
be a line bundle on
![]() $\mathfrak {X}$
. Let
$\mathfrak {X}$
. Let
![]() $H^{\mathrm{ESZ}\text{-}\mathrm{B}}_{\mathcal {L}}$
be the height constructed in [Reference Ellenberg, Satriano and Zureick-Brown6] associated with
$H^{\mathrm{ESZ}\text{-}\mathrm{B}}_{\mathcal {L}}$
be the height constructed in [Reference Ellenberg, Satriano and Zureick-Brown6] associated with
![]() ${\mathcal {L}}$
. Then there is some constant
${\mathcal {L}}$
. Then there is some constant
![]() $C>0$
with
$C>0$
with
That is to say, up to a constant, the stacky heights from Definition 3.10 agree with the ESZ-B heights in [Reference Ellenberg, Satriano and Zureick-Brown6] when the coarse space is
![]() ${\mathbb {P}}^1_{\mathbb {Q}}$
.
${\mathbb {P}}^1_{\mathbb {Q}}$
.
We now explain how the functions
![]() $\phi _m$
and
$\phi _m$
and
![]() $r_m$
can be used to understand the difference between
$r_m$
can be used to understand the difference between
![]() $H_{{\mathcal {L}}}$
and
$H_{{\mathcal {L}}}$
and
![]() $H_{{\mathcal {L}}^{\otimes n}}$
.
$H_{{\mathcal {L}}^{\otimes n}}$
.
Proposition 3.17 Let
![]() $m\in {\mathbb {Z}}_{\geq 1}$
and choose an integer
$m\in {\mathbb {Z}}_{\geq 1}$
and choose an integer
![]() $d\geq 0$
.
$d\geq 0$
.
Proof Since
![]() $\phi _m$
is multiplicative, it suffices to prove the statement for
$\phi _m$
is multiplicative, it suffices to prove the statement for
![]() $x=p^a$
where p is some prime. Note that
$x=p^a$
where p is some prime. Note that
![]() $\phi _m((p^a)^{n}=p^{m-na \ \ \mod m})$
. Therefore,
$\phi _m((p^a)^{n}=p^{m-na \ \ \mod m})$
. Therefore,
![]() $\phi _m((p^a)^{-d \ \ \mod m})=p^{m+da \ \ \mod m}$
. On the other hand,
$\phi _m((p^a)^{-d \ \ \mod m})=p^{m+da \ \ \mod m}$
. On the other hand,
![]() $r_m((p^a)^{d \ \ \mod m}=p^{da \ \ \mod m}=p^{m+da\ \ \mod m}$
as needed.
$r_m((p^a)^{d \ \ \mod m}=p^{da \ \ \mod m}=p^{m+da\ \ \mod m}$
as needed.
The theory of heights is different from the classical theory of heights, as
![]() $H_{{\mathcal {L}}^{-1}}\neq \frac {1}{H_{\mathcal {L}}}+O(1)$
and
$H_{{\mathcal {L}}^{-1}}\neq \frac {1}{H_{\mathcal {L}}}+O(1)$
and
![]() $H_{{\mathcal {L}}^{\otimes n}}\neq (H_{\mathcal {L}})^n+O(1)$
. The functions
$H_{{\mathcal {L}}^{\otimes n}}\neq (H_{\mathcal {L}})^n+O(1)$
. The functions
![]() $\phi _m$
and
$\phi _m$
and
![]() $r_m$
can be used to compute these quantities.
$r_m$
can be used to compute these quantities.
Theorem 3.18 (Duality theorem)
Let
![]() $\mathfrak {X}=\mathfrak {X}(X:(P_1,m_1), \ldots ,(P_r,m_r))$
be a stacky curve, and let
$\mathfrak {X}=\mathfrak {X}(X:(P_1,m_1), \ldots ,(P_r,m_r))$
be a stacky curve, and let
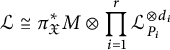 $$\begin{align*}{\mathcal{L}}\cong \pi_{\mathfrak{X}}^*M\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i}\end{align*}$$
$$\begin{align*}{\mathcal{L}}\cong \pi_{\mathfrak{X}}^*M\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i}\end{align*}$$
with
![]() $0\leq d_i\leq m_i-1$
. Fix an integer
$0\leq d_i\leq m_i-1$
. Fix an integer
![]() $n\neq 0$
and write
$n\neq 0$
and write
![]() $n_i=nd_i\ \ \mod m_i$
.
$n_i=nd_i\ \ \mod m_i$
.
-
(1) Then we always have
 $$ \begin{align*} H_{{\mathcal{L}}^{\otimes n}}&=(H_{{\mathcal{L}}}^{\mathrm{st}})^n\cdot \prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t)^{n_i})^{\frac{1}{m_i}}\\ &=(H_{{\mathcal{L}}}^{\mathrm{st}})^n\cdot \prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t)^{nd_i\quad \mod m_i})^{\frac{1}{m_i}}. \end{align*} $$
$$ \begin{align*} H_{{\mathcal{L}}^{\otimes n}}&=(H_{{\mathcal{L}}}^{\mathrm{st}})^n\cdot \prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t)^{n_i})^{\frac{1}{m_i}}\\ &=(H_{{\mathcal{L}}}^{\mathrm{st}})^n\cdot \prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t)^{nd_i\quad \mod m_i})^{\frac{1}{m_i}}. \end{align*} $$
-
(2) If
 $n>0$
, then In particular,
$n>0$
, then In particular, $$ \begin{align*} H_{{\mathcal{L}}^{\otimes -n}}=(H_{{\mathcal{L}}}^{\mathrm{st}})^{-n}\cdot \prod_{i=1}^rr_{m_i}(\lambda(P_i,t)^{nd_i \quad\mod m_i})^{\frac{1}{m_i}}. \end{align*} $$
$$ \begin{align*} H_{{\mathcal{L}}^{\otimes -n}}=(H_{{\mathcal{L}}}^{\mathrm{st}})^{-n}\cdot \prod_{i=1}^rr_{m_i}(\lambda(P_i,t)^{nd_i \quad\mod m_i})^{\frac{1}{m_i}}. \end{align*} $$
 $$\begin{align*}H_{{\mathcal{L}}^{-1}}=(H_{{\mathcal{L}}}^{\mathrm{st}})^{-1}\cdot \prod_{i=1}^rr_{m_i}(\lambda(P_i,t)^{d_i})^{\frac{1}{m_i}}.\end{align*}$$
$$\begin{align*}H_{{\mathcal{L}}^{-1}}=(H_{{\mathcal{L}}}^{\mathrm{st}})^{-1}\cdot \prod_{i=1}^rr_{m_i}(\lambda(P_i,t)^{d_i})^{\frac{1}{m_i}}.\end{align*}$$
Proof Write
![]() $nd_i=m_iq_i+r_i$
with
$nd_i=m_iq_i+r_i$
with
![]() $0\leq r_i<m_i$
. Note that
$0\leq r_i<m_i$
. Note that
![]() ${\mathcal {L}}_{P_i}^{\otimes m_i}=\pi ^*_{\mathfrak {X}} {\mathcal {O}}_X(P_i)$
. So we have that
${\mathcal {L}}_{P_i}^{\otimes m_i}=\pi ^*_{\mathfrak {X}} {\mathcal {O}}_X(P_i)$
. So we have that
 $$ \begin{align} {\mathcal{L}}^{\otimes n}=\pi^*_{\mathfrak{X}}(M^{\otimes n})\cdot\prod_{i=1}^r\pi_{\mathfrak{X}}^*({\mathcal{O}}_X(q_iP_i))\cdot \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes r_i}. \end{align} $$
$$ \begin{align} {\mathcal{L}}^{\otimes n}=\pi^*_{\mathfrak{X}}(M^{\otimes n})\cdot\prod_{i=1}^r\pi_{\mathfrak{X}}^*({\mathcal{O}}_X(q_iP_i))\cdot \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes r_i}. \end{align} $$
Therefore, we have
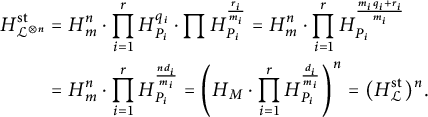 $$ \begin{align*} H_{{\mathcal{L}}^{\otimes n}}^{\mathrm{st}}&=H_m^n\cdot\prod_{i=1}^rH_{P_i}^{q_i}\cdot \prod H_{P_i}^{\frac{r_i}{m_i}}=H_m^n\cdot\prod_{i=1}^rH_{P_i}^{\frac{m_iq_i+r_i}{m_i}}\\ &=H_m^n\cdot\prod_{i=1}^rH_{P_i}^{\frac{nd_i}{m_i}}=\left(H_M\cdot \prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}\right)^n=(H_{{\mathcal{L}}}^{\mathrm{st}})^n. \end{align*} $$
$$ \begin{align*} H_{{\mathcal{L}}^{\otimes n}}^{\mathrm{st}}&=H_m^n\cdot\prod_{i=1}^rH_{P_i}^{q_i}\cdot \prod H_{P_i}^{\frac{r_i}{m_i}}=H_m^n\cdot\prod_{i=1}^rH_{P_i}^{\frac{m_iq_i+r_i}{m_i}}\\ &=H_m^n\cdot\prod_{i=1}^rH_{P_i}^{\frac{nd_i}{m_i}}=\left(H_M\cdot \prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}\right)^n=(H_{{\mathcal{L}}}^{\mathrm{st}})^n. \end{align*} $$
Now we have that
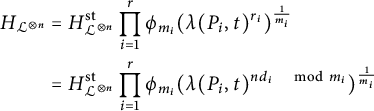 $$ \begin{align*} H_{{\mathcal{L}}^{\otimes n}}&=H_{{\mathcal{L}}^{\otimes n}}^{\mathrm{st}}\prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t)^{r_i})^{\frac{1}{m_i}}\\ &=H_{{\mathcal{L}}^{\otimes n}}^{\mathrm{st}}\prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t)^{nd_i \quad\mod m_i})^{\frac{1}{m_i}} \end{align*} $$
$$ \begin{align*} H_{{\mathcal{L}}^{\otimes n}}&=H_{{\mathcal{L}}^{\otimes n}}^{\mathrm{st}}\prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t)^{r_i})^{\frac{1}{m_i}}\\ &=H_{{\mathcal{L}}^{\otimes n}}^{\mathrm{st}}\prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t)^{nd_i \quad\mod m_i})^{\frac{1}{m_i}} \end{align*} $$
by the definition of the
![]() $r_i$
. Now let
$r_i$
. Now let
![]() $n>0$
. By Proposition 3.17, we have
$n>0$
. By Proposition 3.17, we have
![]() $\phi _m(\lambda (P_i,t)^{-dn \ \ \mod m})=r_m(\lambda (P_i,t)^{nd_i \ \ \mod m_i})$
giving the desired conclusion of (2).
$\phi _m(\lambda (P_i,t)^{-dn \ \ \mod m})=r_m(\lambda (P_i,t)^{nd_i \ \ \mod m_i})$
giving the desired conclusion of (2).
3.2 Integral points on stacky curves
Here, we show that the height functions defined in Definition 3.10) can be used to obtain information about integral points on
![]() $\mathfrak {X}$
. Fix a stacky curve
$\mathfrak {X}$
. Fix a stacky curve
![]() $\mathfrak {X}=\mathfrak {X}(X:({\mathbf {p}},{\mathbf {m}}))$
.
$\mathfrak {X}=\mathfrak {X}(X:({\mathbf {p}},{\mathbf {m}}))$
.
Let
![]() $H_{\mathfrak {X},P_i}$
be the height function associated with the line bundle
$H_{\mathfrak {X},P_i}$
be the height function associated with the line bundle
![]() ${\mathcal {L}}_{P_i}$
and put
${\mathcal {L}}_{P_i}$
and put
![]() ${\mathcal {D}}_{\mathfrak {X}}=\prod _{i=1}^r{\mathcal {L}}_{P_i}.$
Recall that we have
${\mathcal {D}}_{\mathfrak {X}}=\prod _{i=1}^r{\mathcal {L}}_{P_i}.$
Recall that we have
![]() $H_{\mathfrak {X},P_i}(t)=\phi _{m_i}(\lambda (P_i,t))^{1/m_i}$
. We will work with the height
$H_{\mathfrak {X},P_i}(t)=\phi _{m_i}(\lambda (P_i,t))^{1/m_i}$
. We will work with the height
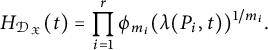 $$\begin{align*}H_{{\mathcal{D}}_{\mathfrak{X}}}(t)=\prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t))^{1/m_i}.\end{align*}$$
$$\begin{align*}H_{{\mathcal{D}}_{\mathfrak{X}}}(t)=\prod_{i=1}^r\phi_{m_i}(\lambda(P_i,t))^{1/m_i}.\end{align*}$$
This is the stacky part of the anti-canonical height. We will prove that the set of integral points is contained in the set of points where
![]() $H_{{\mathcal {D}}_{\mathfrak {X}}}(t)=1$
. When we take
$H_{{\mathcal {D}}_{\mathfrak {X}}}(t)=1$
. When we take
![]() $K={\mathbb {Q}}$
, we see that this condition is sufficient. In other words, the S-integral points are those where the stacky part of the height is trivial. Following Darmon [Reference Darmon4], we have the following notion of integral points on an stacky curve.
$K={\mathbb {Q}}$
, we see that this condition is sufficient. In other words, the S-integral points are those where the stacky part of the height is trivial. Following Darmon [Reference Darmon4], we have the following notion of integral points on an stacky curve.
Definition 3.19 (Darmon)
Let
![]() $\mathfrak {X}=(X:(P_1,m_1), \ldots , (P_r,m_r))$
be a stacky curve over a number field K, S a finite set of places of K containing all primes of bad reduction. Let
$\mathfrak {X}=(X:(P_1,m_1), \ldots , (P_r,m_r))$
be a stacky curve over a number field K, S a finite set of places of K containing all primes of bad reduction. Let
![]() $\underline {X}$
be a smooth proper model for X over
$\underline {X}$
be a smooth proper model for X over
![]() ${\mathcal {O}}_{K,S}$
. The
${\mathcal {O}}_{K,S}$
. The
![]() $(\underline {X},S)$
-integral points of
$(\underline {X},S)$
-integral points of
![]() $\mathfrak {X}$
(usually abbreviated to S-integral points of
$\mathfrak {X}$
(usually abbreviated to S-integral points of
![]() $\mathfrak {X}$
) are the points
$\mathfrak {X}$
) are the points
![]() $t\in X(K)$
such that
$t\in X(K)$
such that
for all
![]() $P\in X(K)$
and
$P\in X(K)$
and
![]() $\nu \notin S$
.
$\nu \notin S$
.
We shall prove the following theorem.
Theorem 3.20 Let
![]() $\mathfrak {X}=(X:(P_1,m_1), \ldots ,(P_r,m_r))$
be a stacky curve over K satisfying our assumptions and choose S and a model
$\mathfrak {X}=(X:(P_1,m_1), \ldots ,(P_r,m_r))$
be a stacky curve over K satisfying our assumptions and choose S and a model
![]() $\underline {X}$
as we have specified. Then we have the following conclusions.
$\underline {X}$
as we have specified. Then we have the following conclusions.
-
(1)
where $$\begin{align*}\mathfrak{X}({\mathcal{O}}_{K,S,\underline{X}})\subseteq \bigcap_{i=1}^r\mathfrak{X}(P_i;K),\end{align*}$$
$$\begin{align*}\mathfrak{X}({\mathcal{O}}_{K,S,\underline{X}})\subseteq \bigcap_{i=1}^r\mathfrak{X}(P_i;K),\end{align*}$$
 $\mathfrak {X}(P_i;K)=\{t\in X(K)\colon H_{\mathfrak {X},P_i}(t)=1\}$
.
$\mathfrak {X}(P_i;K)=\{t\in X(K)\colon H_{\mathfrak {X},P_i}(t)=1\}$
.
-
(2) If
 $K={\mathbb {Q}}$
, then In particular, the set of S-integral points of
$K={\mathbb {Q}}$
, then In particular, the set of S-integral points of $$\begin{align*}\mathfrak{X}({\mathcal{O}}_{K,S,\underline{X}})= \bigcap_{i=1}^r\mathfrak{X}(P_i;K). \end{align*}$$
$$\begin{align*}\mathfrak{X}({\mathcal{O}}_{K,S,\underline{X}})= \bigcap_{i=1}^r\mathfrak{X}(P_i;K). \end{align*}$$
 $\mathfrak {X}$
is precisely the set of points where
$\mathfrak {X}$
is precisely the set of points where
 $H_{\mathfrak {X},P_i}(t)=1$
for all
$H_{\mathfrak {X},P_i}(t)=1$
for all
 $i=1,...,r$
.
$i=1,...,r$
.
Fix a prime
![]() $\nu \notin S$
and write
$\nu \notin S$
and write
![]() $(t\cdot P)_\nu =m_{P}^{e_{\nu ,P}(t)}\cdot q_{\nu ,P}(t)$
where
$(t\cdot P)_\nu =m_{P}^{e_{\nu ,P}(t)}\cdot q_{\nu ,P}(t)$
where
![]() $e_{\nu ,P}(t)\geq 0$
and
$e_{\nu ,P}(t)\geq 0$
and
![]() $q_{\nu ,P}(t)\geq 0$
is not divisible by
$q_{\nu ,P}(t)\geq 0$
is not divisible by
![]() $m_P$
. In other words,
$m_P$
. In other words,
![]() $q_{\nu ,P}(t)$
is the
$q_{\nu ,P}(t)$
is the
![]() $m_P$
-free part of
$m_P$
-free part of
![]() $(t\cdot P)_\nu $
. Set
$(t\cdot P)_\nu $
. Set
![]() $\mathrm {N}(\mathfrak {p}_\nu )=p_\nu ^{f(\nu )}$
. Then
$\mathrm {N}(\mathfrak {p}_\nu )=p_\nu ^{f(\nu )}$
. Then
and
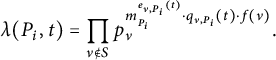 $$ \begin{align} \lambda(P_i,t)=\prod_{\nu\notin S}p_\nu^{m_{P_i}^{e_{\nu,P_i}(t)}\cdot q_{\nu,P_i}(t)\cdot f(\nu)}. \end{align} $$
$$ \begin{align} \lambda(P_i,t)=\prod_{\nu\notin S}p_\nu^{m_{P_i}^{e_{\nu,P_i}(t)}\cdot q_{\nu,P_i}(t)\cdot f(\nu)}. \end{align} $$
Using the functions
![]() $\lambda (P,t)$
, we can find subsets of the rational points that contain all integral points.
$\lambda (P,t)$
, we can find subsets of the rational points that contain all integral points.
Proposition 3.21 Suppose that
![]() $m_P>1$
. Define
$m_P>1$
. Define
![]() $\mathfrak {X}(P;K)=\{t\in X(K)\colon H_{\mathfrak {X},P}(t)=1\}$
. Then
$\mathfrak {X}(P;K)=\{t\in X(K)\colon H_{\mathfrak {X},P}(t)=1\}$
. Then
Proof Note that
![]() $H_{\mathfrak {X},P}(t)=1$
is equivalent to
$H_{\mathfrak {X},P}(t)=1$
is equivalent to
![]() $\phi _{m_P}(\lambda (P,t))=1$
, which is then equivalent to
$\phi _{m_P}(\lambda (P,t))=1$
, which is then equivalent to
![]() $r_{m_P}(\lambda (P,t))=1$
. Suppose now that t is an S-integral point. Then
$r_{m_P}(\lambda (P,t))=1$
. Suppose now that t is an S-integral point. Then
![]() $(t\cdot P)_\nu \equiv 0\ \ \mod m_{P}\Rightarrow e_{\nu ,P}(t)>0$
for all
$(t\cdot P)_\nu \equiv 0\ \ \mod m_{P}\Rightarrow e_{\nu ,P}(t)>0$
for all
![]() $\nu \notin S$
. Thus,
$\nu \notin S$
. Thus,
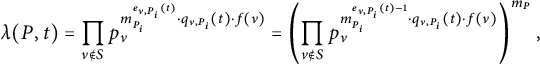 $$\begin{align*}\lambda(P,t)=\prod_{\nu\notin S}p_\nu^{m_{P_i}^{e_{\nu,P_i}(t)}\cdot q_{\nu,P_i}(t)\cdot f(\nu)}=\left(\prod_{v\notin S}p_\nu^{m_{P_i}^{e_{\nu,P_i}(t)-1}\cdot q_{\nu,P_i}(t)\cdot f(\nu)}\right)^{m_P},\end{align*}$$
$$\begin{align*}\lambda(P,t)=\prod_{\nu\notin S}p_\nu^{m_{P_i}^{e_{\nu,P_i}(t)}\cdot q_{\nu,P_i}(t)\cdot f(\nu)}=\left(\prod_{v\notin S}p_\nu^{m_{P_i}^{e_{\nu,P_i}(t)-1}\cdot q_{\nu,P_i}(t)\cdot f(\nu)}\right)^{m_P},\end{align*}$$
whence
![]() $H_{\mathfrak {X},P}(t)=1$
as
$H_{\mathfrak {X},P}(t)=1$
as
![]() $\lambda (P,t)$
is an
$\lambda (P,t)$
is an
![]() $m_P$
-power.
$m_P$
-power.
We see that each point P with multiplicity
![]() $m_P>1$
imposes a height dropping condition on the set of integral points. Thus, to study integral points, it suffices to study
$m_P>1$
imposes a height dropping condition on the set of integral points. Thus, to study integral points, it suffices to study
We obtain the following, that the stacky part of the anti-canonical height cuts out the integral points.
Corollary 3.22 Let
![]() $\mathfrak {X}=\mathfrak {X}(X:({\mathbf {p}},{\mathbf {m}}))$
be a stacky curve and
$\mathfrak {X}=\mathfrak {X}(X:({\mathbf {p}},{\mathbf {m}}))$
be a stacky curve and
![]() ${\mathcal {D}}_{\mathfrak {X}}=\prod _{i=1}^r{\mathcal {L}}_{P_i}$
. Then
${\mathcal {D}}_{\mathfrak {X}}=\prod _{i=1}^r{\mathcal {L}}_{P_i}$
. Then
In other words, the integral points are precisely those points where the stacky part of the anti-canonical height vanishes.
Example 3.23 Let
![]() $X=C$
be an elliptic curve. Then
$X=C$
be an elliptic curve. Then
![]() $H_{{\mathcal {D}}_{\mathfrak {X}}}=H_{-K_{\mathfrak {X}}}$
. In other words, the integral points of the stacky elliptic curve are precisely the points where the anti-canonical height vanishes. Since
$H_{{\mathcal {D}}_{\mathfrak {X}}}=H_{-K_{\mathfrak {X}}}$
. In other words, the integral points of the stacky elliptic curve are precisely the points where the anti-canonical height vanishes. Since
![]() $\phi _m(x)=1\iff r_m(x)=1$
, we have that the S-integral points of a stacky elliptic curve are also precisely the points where the stacky canonical height vanishes. If
$\phi _m(x)=1\iff r_m(x)=1$
, we have that the S-integral points of a stacky elliptic curve are also precisely the points where the stacky canonical height vanishes. If
![]() $\mathfrak {X}$
is a scheme and X is an elliptic curve, then this is certainly true, as the canonical height is trivial and every rational point is integral, and vice versa.
$\mathfrak {X}$
is a scheme and X is an elliptic curve, then this is certainly true, as the canonical height is trivial and every rational point is integral, and vice versa.
Proof of Theorem 3.20
We have already shown part
![]() $(1)$
of Theorem 3.20 in (3.21). We turn to part
$(1)$
of Theorem 3.20 in (3.21). We turn to part
![]() $(2)$
and assume that
$(2)$
and assume that
![]() $K={\mathbb {Q}}$
. We know that
$K={\mathbb {Q}}$
. We know that
![]() $\bigcap _{m_P>1}\mathfrak {X}(P;{\mathbb {Q}})\subseteq \mathfrak {X}({\mathcal {O}}_{{\mathbb {Q}},S,\underline {X}})$
by (3.21). We now show the reverse inclusion. Let
$\bigcap _{m_P>1}\mathfrak {X}(P;{\mathbb {Q}})\subseteq \mathfrak {X}({\mathcal {O}}_{{\mathbb {Q}},S,\underline {X}})$
by (3.21). We now show the reverse inclusion. Let
![]() $t\in X({\mathbb {Q}})$
with
$t\in X({\mathbb {Q}})$
with
![]() $H_{\mathfrak {X},P}(t)=1$
for all P with
$H_{\mathfrak {X},P}(t)=1$
for all P with
![]() $m_P>1$
. Since
$m_P>1$
. Since
![]() $K={\mathbb {Q}}$
, we have that
$K={\mathbb {Q}}$
, we have that
![]() $\mathrm {N}(\mathfrak {p}_\nu )=p_\nu $
and
$\mathrm {N}(\mathfrak {p}_\nu )=p_\nu $
and
![]() $f(\nu )=1$
for all finite places
$f(\nu )=1$
for all finite places
![]() $\nu $
. Fix P with
$\nu $
. Fix P with
![]() $m_P>1$
. Toward a contradiction suppose that
$m_P>1$
. Toward a contradiction suppose that
![]() $(t\cdot P)_{\nu _0}\neq 0 \ \ \mod m_P$
for some
$(t\cdot P)_{\nu _0}\neq 0 \ \ \mod m_P$
for some
![]() $\nu _0\notin S$
. Then
$\nu _0\notin S$
. Then
![]() $e_{\nu _0,P}(t)=0$
. Notice that
$e_{\nu _0,P}(t)=0$
. Notice that
![]() $H_{\mathfrak {X},P}(t)=1$
means that
$H_{\mathfrak {X},P}(t)=1$
means that
![]() $\lambda (P,t)$
is an
$\lambda (P,t)$
is an
![]() $m_P$
-power. Since if
$m_P$
-power. Since if
![]() $\nu \neq \nu ^\prime $
we have that
$\nu \neq \nu ^\prime $
we have that
![]() $p_\nu \neq p_{\nu ^{\prime }}$
, we have by unique factorization of integers that
$p_\nu \neq p_{\nu ^{\prime }}$
, we have by unique factorization of integers that
 $$\begin{align*}\lambda(P,t)=\prod_{\nu\notin S}p_\nu^{m_{P}^{e_{\nu,P}(t)}\cdot q_{\nu,P}(t)}=(\prod_{\nu\notin S}p_\nu^{z_\nu(t)})^{m_P}\end{align*}$$
$$\begin{align*}\lambda(P,t)=\prod_{\nu\notin S}p_\nu^{m_{P}^{e_{\nu,P}(t)}\cdot q_{\nu,P}(t)}=(\prod_{\nu\notin S}p_\nu^{z_\nu(t)})^{m_P}\end{align*}$$
for some integers
![]() $z_\nu (t)$
. In particular, for
$z_\nu (t)$
. In particular, for
![]() $\nu _0$
, we have
$\nu _0$
, we have
Thus,
![]() $z_{\nu _0}(t)m_P=q_{\nu _0,P}(t)$
, which contradicts
$z_{\nu _0}(t)m_P=q_{\nu _0,P}(t)$
, which contradicts
![]() $q_{\nu _0,P}(t)$
being indivisible by
$q_{\nu _0,P}(t)$
being indivisible by
![]() $m_P$
. Thus, for all
$m_P$
. Thus, for all
![]() $m_P>1$
and
$m_P>1$
and
![]() $\nu \notin S$
, we have
$\nu \notin S$
, we have
![]() $(t\cdot P)_\nu \equiv 0 \ \ \mod m_P$
and t is an S-integral point of
$(t\cdot P)_\nu \equiv 0 \ \ \mod m_P$
and t is an S-integral point of
![]() $\mathfrak {X}$
by definition.
$\mathfrak {X}$
by definition.
4 Stacky curves with coarse space
 ${\mathbb {P}}^1$
${\mathbb {P}}^1$
We focus on the situation when the base curve is
![]() ${\mathbb {P}}^1$
. Let
${\mathbb {P}}^1$
. Let
![]() $X={\mathbb {P}}^1_{\mathbb {Q}}$
and
$X={\mathbb {P}}^1_{\mathbb {Q}}$
and
![]() $S=\{\nu _\infty \}$
and take
$S=\{\nu _\infty \}$
and take
![]() ${\mathcal {L}}$
to be
${\mathcal {L}}$
to be
![]() ${\mathcal {O}}_{{\mathbb {P}}^1}(1)$
, so the ample height is the usual one. We consider the stacky curve
${\mathcal {O}}_{{\mathbb {P}}^1}(1)$
, so the ample height is the usual one. We consider the stacky curve
In this situation, the
![]() $\lambda (P,t)$
can be easily computed.
$\lambda (P,t)$
can be easily computed.
Proposition 4.1 Let
![]() $t=[x:y]$
and suppose that
$t=[x:y]$
and suppose that
![]() $P_i=(a_i:b_i)$
where
$P_i=(a_i:b_i)$
where
![]() $a_i,b_i$
are coprime integers. Then
$a_i,b_i$
are coprime integers. Then
![]() $\lambda (P_i,t)=\mid a_iy-b_ix\mid .$
$\lambda (P_i,t)=\mid a_iy-b_ix\mid .$
Proof We have that
![]() $(t\cdot P_i)_p=\max _n\{[x:y]\equiv [a_i:b_i]\ \ \mod p^n\}$
. Note that this means there is some
$(t\cdot P_i)_p=\max _n\{[x:y]\equiv [a_i:b_i]\ \ \mod p^n\}$
. Note that this means there is some
![]() $\lambda \neq 0\ \ \mod p^n$
with
$\lambda \neq 0\ \ \mod p^n$
with
![]() $(x,y)=\lambda (a_i,b_i)\ \ \mod p^n$
. Since
$(x,y)=\lambda (a_i,b_i)\ \ \mod p^n$
. Since
![]() $a_i,b_i$
have been taken coprime, we may assume that p does not divide
$a_i,b_i$
have been taken coprime, we may assume that p does not divide
![]() $a_i$
or
$a_i$
or
![]() $b_i$
. Suppose that
$b_i$
. Suppose that
![]() $p\nmid a_i$
(the other case is similar). Then
$p\nmid a_i$
(the other case is similar). Then
![]() $\lambda =\frac {x}{a_i} \ \ \mod p^n$
and therefore
$\lambda =\frac {x}{a_i} \ \ \mod p^n$
and therefore
![]() $b_ix-a_iy= 0 \ \ \mod p^n$
. Thus,
$b_ix-a_iy= 0 \ \ \mod p^n$
. Thus,
![]() $(t\cdot P_i)_p=\operatorname {ord}_p(b_ix-a_iy)$
. Then we have that
$(t\cdot P_i)_p=\operatorname {ord}_p(b_ix-a_iy)$
. Then we have that
as needed.
Definition 4.2 (Euler characteristic of stacky curves [Reference Darmon4])
Let
![]() $\mathfrak {X}=(X:(P_1,m_1), \ldots ,(P_r,m_r))$
be a stacky curve. The Euler characteristic of
$\mathfrak {X}=(X:(P_1,m_1), \ldots ,(P_r,m_r))$
be a stacky curve. The Euler characteristic of
![]() $\mathfrak {X}$
is defined by the formula
$\mathfrak {X}$
is defined by the formula
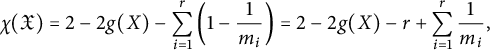 $$\begin{align*}\chi(\mathfrak{X})=2-2g(X)-\sum_{i=1}^r \left(1-\dfrac{1}{m_{i}} \right)=2-2g(X)-r+\sum_{i=1}^r\dfrac{1}{m_{i}},\end{align*}$$
$$\begin{align*}\chi(\mathfrak{X})=2-2g(X)-\sum_{i=1}^r \left(1-\dfrac{1}{m_{i}} \right)=2-2g(X)-r+\sum_{i=1}^r\dfrac{1}{m_{i}},\end{align*}$$
where
![]() $g(X)$
is the genus of the curve X. We define the genus of a stacky curve by the formula
$g(X)$
is the genus of the curve X. We define the genus of a stacky curve by the formula
![]() $\chi (\mathfrak {X})=2-2g(\mathfrak {X})$
.
$\chi (\mathfrak {X})=2-2g(\mathfrak {X})$
.
We now begin assembling the necessary ingredients to compare our heights constructed in Section 3 to those in [Reference Ellenberg, Satriano and Zureick-Brown6]. We first work with
![]() $H_{{\mathcal {L}}}^{\mathrm {st}}$
.
$H_{{\mathcal {L}}}^{\mathrm {st}}$
.
Proposition 4.3 Let
![]() $\mathfrak {X}=\mathfrak {X}(X:(P_1, \ldots ,P_r),(m_1, \ldots , m_r))$
, and let
$\mathfrak {X}=\mathfrak {X}(X:(P_1, \ldots ,P_r),(m_1, \ldots , m_r))$
, and let
![]() ${\mathcal {L}}$
be a line bundle on
${\mathcal {L}}$
be a line bundle on
![]() $\mathfrak {X}$
with
$\mathfrak {X}$
with
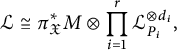 $$\begin{align*}{\mathcal{L}}\cong \pi_{\mathfrak{X}}^*M\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i},\end{align*}$$
$$\begin{align*}{\mathcal{L}}\cong \pi_{\mathfrak{X}}^*M\otimes \prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i},\end{align*}$$
where
![]() $0\leq d_i<m_i$
and M is a line bundle on X with
$0\leq d_i<m_i$
and M is a line bundle on X with
![]() $\pi _{\mathfrak {X}}$
being the coarse space map. Let
$\pi _{\mathfrak {X}}$
being the coarse space map. Let
![]() $H_{{\mathcal {L}}}^{\mathrm {st},\mathrm{ESZ}\text{-}\mathrm{B}}$
be the stable height as constructed in [Reference Ellenberg, Satriano and Zureick-Brown6]. Then
$H_{{\mathcal {L}}}^{\mathrm {st},\mathrm{ESZ}\text{-}\mathrm{B}}$
be the stable height as constructed in [Reference Ellenberg, Satriano and Zureick-Brown6]. Then
![]() $H_{{\mathcal {L}}}^{\mathrm {st}}=H_{{\mathcal {L}}}^{\mathrm {st},\mathrm{ESZ}\text{-}\mathrm{B}}$
.
$H_{{\mathcal {L}}}^{\mathrm {st}}=H_{{\mathcal {L}}}^{\mathrm {st},\mathrm{ESZ}\text{-}\mathrm{B}}$
.
Proof In [Reference Ellenberg, Satriano and Zureick-Brown6], a general definition of the stable height is given. Let
![]() $m=\prod _{i=1}^rm_i$
. By the properties of the stable height described in [Reference Ellenberg, Satriano and Zureick-Brown6], we have that
$m=\prod _{i=1}^rm_i$
. By the properties of the stable height described in [Reference Ellenberg, Satriano and Zureick-Brown6], we have that
On the other hand,
It is a fact that if L is a line bundle on X, then
![]() $H^{\mathrm {st},\mathrm{ESZ}\text{-}\mathrm{B}}_{\pi _{\mathfrak {X}}^* L}=H_L\circ \pi _{\mathfrak {X}}$
. Therefore, we have
$H^{\mathrm {st},\mathrm{ESZ}\text{-}\mathrm{B}}_{\pi _{\mathfrak {X}}^* L}=H_L\circ \pi _{\mathfrak {X}}$
. Therefore, we have
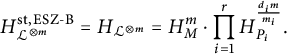 $$\begin{align*}H^{\mathrm{st},\mathrm{ESZ}\text{-}\mathrm{B}}_{{\mathcal{L}}^{\otimes m}}=H_{{\mathcal{L}}^{\otimes m}}=H_{M}^m\cdot \prod _{i=1}^rH_{P_i}^{\frac{d_i m}{m_i}}.\end{align*}$$
$$\begin{align*}H^{\mathrm{st},\mathrm{ESZ}\text{-}\mathrm{B}}_{{\mathcal{L}}^{\otimes m}}=H_{{\mathcal{L}}^{\otimes m}}=H_{M}^m\cdot \prod _{i=1}^rH_{P_i}^{\frac{d_i m}{m_i}}.\end{align*}$$
Taking
![]() $m{\mathrm {th}}$
roots gives the desired inequality.
$m{\mathrm {th}}$
roots gives the desired inequality.
Corollary 4.4 Let
![]() $\mathfrak {X}=\mathfrak {X}({\mathbb {P}}^1:(P_1, \ldots ,P_r),(m_1, \ldots , m_r)))$
, and let
$\mathfrak {X}=\mathfrak {X}({\mathbb {P}}^1:(P_1, \ldots ,P_r),(m_1, \ldots , m_r)))$
, and let
![]() ${\mathcal {L}}$
be a line bundle on
${\mathcal {L}}$
be a line bundle on
![]() $\mathfrak {X}$
. Then
$\mathfrak {X}$
. Then
Proof Let
![]() ${\mathcal {L}}$
be a line bundle on
${\mathcal {L}}$
be a line bundle on
![]() $\mathfrak {X}$
. Then we may write
$\mathfrak {X}$
. Then we may write
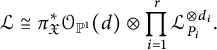 $$\begin{align*}{\mathcal{L}}\cong \pi_{\mathfrak{X}}^*{\mathcal{O}}_{{\mathbb{P}}^1}(d)\otimes\prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i}. \end{align*}$$
$$\begin{align*}{\mathcal{L}}\cong \pi_{\mathfrak{X}}^*{\mathcal{O}}_{{\mathbb{P}}^1}(d)\otimes\prod_{i=1}^r{\mathcal{L}}_{P_i}^{\otimes d_i}. \end{align*}$$
On
![]() ${\mathbb {P}}^1$
, we have that
${\mathbb {P}}^1$
, we have that
![]() ${\mathcal {O}}_{{\mathbb {P}}^1}(P_i)\cong {\mathcal {O}}_{{\mathbb {P}}^1}(1)$
. So, by definition, the stable height is
${\mathcal {O}}_{{\mathbb {P}}^1}(P_i)\cong {\mathcal {O}}_{{\mathbb {P}}^1}(1)$
. So, by definition, the stable height is
as needed.
We can now precisely define the heights on a stacky curve with coarse space
![]() ${\mathbb {P}}^1_{\mathbb {Q}}$
.
${\mathbb {P}}^1_{\mathbb {Q}}$
.
Definition 4.5 Let
![]() $\mathfrak {X}=({\mathbb {P}}^1_{\mathbb {Q}},(P_1,m_1), \ldots ,(P_r,m_r))$
be a stacky curve. Set
$\mathfrak {X}=({\mathbb {P}}^1_{\mathbb {Q}},(P_1,m_1), \ldots ,(P_r,m_r))$
be a stacky curve. Set
![]() $P_i=[a_i:b_i]$
with
$P_i=[a_i:b_i]$
with
![]() $a_i,b_i$
coprime integers and
$a_i,b_i$
coprime integers and
![]() $\ell _i(t)=ax-by$
when
$\ell _i(t)=ax-by$
when
![]() $t=[x:y]$
for
$t=[x:y]$
for
![]() $x,y$
coprime integers. Let
$x,y$
coprime integers. Let
![]() ${\mathcal {L}}=\pi _{\mathfrak {X}}^* M\otimes \prod _{i=1}^r{\mathcal {L}}_{P_i}^{\otimes d_i}$
with
${\mathcal {L}}=\pi _{\mathfrak {X}}^* M\otimes \prod _{i=1}^r{\mathcal {L}}_{P_i}^{\otimes d_i}$
with
![]() $0\leq d_i<m_i$
. Then define
$0\leq d_i<m_i$
. Then define
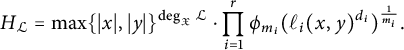 $$\begin{align*}H_{\mathcal{L}}=\max\{\vert x\vert,\vert y\vert\}^{\deg_{\mathfrak{X}} {\mathcal{L}}}\cdot \prod_{i=1}^r\phi_{m_i}(\ell_i(x,y)^{d_i})^{\frac{1}{m_i}}.\end{align*}$$
$$\begin{align*}H_{\mathcal{L}}=\max\{\vert x\vert,\vert y\vert\}^{\deg_{\mathfrak{X}} {\mathcal{L}}}\cdot \prod_{i=1}^r\phi_{m_i}(\ell_i(x,y)^{d_i})^{\frac{1}{m_i}}.\end{align*}$$
In particular, we have that
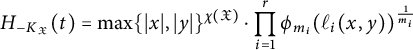 $$\begin{align*}H_{-K_{\mathfrak{X}}}(t)=\max\{\vert x\vert,\vert y\vert\}^{\chi(\mathfrak{X})}\cdot \prod_{i=1}^r\phi_{m_i}(\ell_i(x,y))^{\frac{1}{m_i}} \end{align*}$$
$$\begin{align*}H_{-K_{\mathfrak{X}}}(t)=\max\{\vert x\vert,\vert y\vert\}^{\chi(\mathfrak{X})}\cdot \prod_{i=1}^r\phi_{m_i}(\ell_i(x,y))^{\frac{1}{m_i}} \end{align*}$$
and
 $$\begin{align*}H_{K_{\mathfrak{X}}}(t)=\max\{\vert x\vert,\vert y\vert\}^{-\chi(\mathfrak{X})}\cdot \prod_{i=1}^rr_{m_i}(\ell_i(x,y))^{\frac{1}{m_i}}.\end{align*}$$
$$\begin{align*}H_{K_{\mathfrak{X}}}(t)=\max\{\vert x\vert,\vert y\vert\}^{-\chi(\mathfrak{X})}\cdot \prod_{i=1}^rr_{m_i}(\ell_i(x,y))^{\frac{1}{m_i}}.\end{align*}$$
When
![]() $P_1=[1,0],P_2=[1,-1],P_3=[1:0]$
, and
$P_1=[1,0],P_2=[1,-1],P_3=[1:0]$
, and
![]() $m_1=m_2=m_3=2$
, we obtain the square root of the height function Question (2.7). We now have enough to prove our main comparison theorem.
$m_1=m_2=m_3=2$
, we obtain the square root of the height function Question (2.7). We now have enough to prove our main comparison theorem.
4.1 Proof of Theorem 3.16
We follow the argument given in [Reference Ellenberg, Satriano and Zureick-Brown6, p. 45]. Write
![]() ${\mathcal {L}}\cong \pi _{\mathfrak {X}}^*M\otimes \prod _{i=1}^r{\mathcal {L}}_{P_i}^{\otimes d_i}$
. From [Reference Ellenberg, Satriano and Zureick-Brown6, Section 2.3], we have a decomposition
${\mathcal {L}}\cong \pi _{\mathfrak {X}}^*M\otimes \prod _{i=1}^r{\mathcal {L}}_{P_i}^{\otimes d_i}$
. From [Reference Ellenberg, Satriano and Zureick-Brown6, Section 2.3], we have a decomposition
 $$ \begin{align} \frac{H_{{\mathcal{L}}}^{\mathrm{ESZ}\text{-}\mathrm{B}}}{H_{{\mathcal{L}}}^{\mathrm{st},\mathrm{ESZ}\text{-}\mathrm{B}}} =\prod_p\delta_{{\mathcal{L}},p}, \end{align} $$
$$ \begin{align} \frac{H_{{\mathcal{L}}}^{\mathrm{ESZ}\text{-}\mathrm{B}}}{H_{{\mathcal{L}}}^{\mathrm{st},\mathrm{ESZ}\text{-}\mathrm{B}}} =\prod_p\delta_{{\mathcal{L}},p}, \end{align} $$
where the
![]() $\delta _{{\mathcal {L}},p}$
’s are the local discrepancies associated with
$\delta _{{\mathcal {L}},p}$
’s are the local discrepancies associated with
![]() $H_{{\mathcal {L}}}^{\mathrm{ESZ}\text{-}\mathrm{B}}$
. On the other hand, we have that
$H_{{\mathcal {L}}}^{\mathrm{ESZ}\text{-}\mathrm{B}}$
. On the other hand, we have that
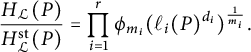 $$ \begin{align} \frac{H_{\mathcal{L}}(P)}{H^{\mathrm{st}}_{\mathcal{L}}(P)} =\prod_{i=1}^r\phi_{m_i}(\ell_i(P)^{d_i})^{\frac{1}{m_i}}. \end{align} $$
$$ \begin{align} \frac{H_{\mathcal{L}}(P)}{H^{\mathrm{st}}_{\mathcal{L}}(P)} =\prod_{i=1}^r\phi_{m_i}(\ell_i(P)^{d_i})^{\frac{1}{m_i}}. \end{align} $$
By Proposition 4.3, we have that
up to some positive constant. Therefore, it suffices to show that
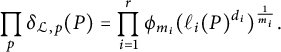 $$\begin{align*}\prod_p\delta_{{\mathcal{L}},p}(P)=\prod_{i=1}^r \phi_{m_i}(\ell_i(P)^{d_i})^{\frac{1}{m_i}}.\end{align*}$$
$$\begin{align*}\prod_p\delta_{{\mathcal{L}},p}(P)=\prod_{i=1}^r \phi_{m_i}(\ell_i(P)^{d_i})^{\frac{1}{m_i}}.\end{align*}$$
Let
![]() $x\colon \mathrm {spec}\ {\mathbb {Q}}\rightarrow \mathfrak {X}$
be a rational point whose image is not any of the stacky points
$x\colon \mathrm {spec}\ {\mathbb {Q}}\rightarrow \mathfrak {X}$
be a rational point whose image is not any of the stacky points
![]() $P_i$
. Then, in [Reference Ellenberg, Satriano and Zureick-Brown6], there is a one-dimensional stack
$P_i$
. Then, in [Reference Ellenberg, Satriano and Zureick-Brown6], there is a one-dimensional stack
![]() ${\mathcal {C}}$
called the tuning stack and a diagram:
${\mathcal {C}}$
called the tuning stack and a diagram:
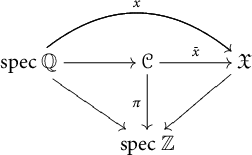
Moreover, the local discrepancies can be computed at a prime p by
These degrees can be computed locally on
![]() $\mathfrak {X}$
in terms of the stacky points
$\mathfrak {X}$
in terms of the stacky points
![]() $P_i$
. In other words,
$P_i$
. In other words,
 $$ \begin{align*} \deg \bar{x}^* {\mathcal{L}}^{-1}&=\sum_{i=1}^r\deg_{P_i}\bar{x}^*{\mathcal{L}}^{-1},\\ \deg\pi_*\bar{x}^*{\mathcal{L}}^{-1}&=\sum_{i=1}^r\deg_{P_i}\pi_*\bar{x}^*{\mathcal{L}}^{-1}. \end{align*} $$
$$ \begin{align*} \deg \bar{x}^* {\mathcal{L}}^{-1}&=\sum_{i=1}^r\deg_{P_i}\bar{x}^*{\mathcal{L}}^{-1},\\ \deg\pi_*\bar{x}^*{\mathcal{L}}^{-1}&=\sum_{i=1}^r\deg_{P_i}\pi_*\bar{x}^*{\mathcal{L}}^{-1}. \end{align*} $$
The local degree of
![]() ${\mathcal {L}}$
at
${\mathcal {L}}$
at
![]() $P_i$
at
$P_i$
at
![]() ${\mathbb {Q}}/{\mathbb {Z}}$
is
${\mathbb {Q}}/{\mathbb {Z}}$
is
![]() $\frac {d_i}{m_i}$
. Following [Reference Ellenberg, Satriano and Zureick-Brown6], we have the local degrees
$\frac {d_i}{m_i}$
. Following [Reference Ellenberg, Satriano and Zureick-Brown6], we have the local degrees
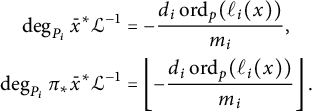 $$ \begin{align*} \deg_{P_i} \bar{x}^*{\mathcal{L}}^{-1}&=-\frac{d_i\operatorname{ord}_p(\ell_i(x))}{m_i},\\ \deg_{P_i} \pi_*\bar{x}^*{\mathcal{L}}^{-1}&=\left\lfloor-\frac{d_i\operatorname{ord}_p(\ell_i(x))}{m_i}\right\rfloor. \end{align*} $$
$$ \begin{align*} \deg_{P_i} \bar{x}^*{\mathcal{L}}^{-1}&=-\frac{d_i\operatorname{ord}_p(\ell_i(x))}{m_i},\\ \deg_{P_i} \pi_*\bar{x}^*{\mathcal{L}}^{-1}&=\left\lfloor-\frac{d_i\operatorname{ord}_p(\ell_i(x))}{m_i}\right\rfloor. \end{align*} $$
We obtain that the contribution at
![]() $P_i$
to the local discrepancy at p can be written as
$P_i$
to the local discrepancy at p can be written as
Now write
![]() $d_i\ell _i(x)=q_im_i+r_i$
with
$d_i\ell _i(x)=q_im_i+r_i$
with
![]() $0\leq r_i\leq m_i-1$
. First, suppose that
$0\leq r_i\leq m_i-1$
. First, suppose that
![]() $r_i=0$
. Then
$r_i=0$
. Then
 $$\begin{align*}\left\lceil \frac{d_i\ell_i(x)}{m_i}\right\rceil-\frac{d_i\ell_i(x)}{m_i}=\left\lceil\frac{q_im_i}{m_i} \right\rceil-\frac{q_im_i}{m_i}=q_i-q_i=0.\end{align*}$$
$$\begin{align*}\left\lceil \frac{d_i\ell_i(x)}{m_i}\right\rceil-\frac{d_i\ell_i(x)}{m_i}=\left\lceil\frac{q_im_i}{m_i} \right\rceil-\frac{q_im_i}{m_i}=q_i-q_i=0.\end{align*}$$
Now suppose that
![]() $r_i\neq 0$
. Then we have that
$r_i\neq 0$
. Then we have that
 $$ \begin{align*} \left\lceil \frac{d_i\ell_i(x)}{m_i}\right\rceil-\frac{d_i\ell_i(x)}{m_i}&=\left\lceil \frac{q_im_i+r_i}{m_i}\right\rceil-\frac{q_im_i+r_i}{m_i}\\ &=q_i+\left\lceil\frac{r_i}{m_i}\right\rceil-\frac{r_i}{m_i}-q_i\\ &=1-\frac{r_i}{m_i}=\frac{m_i-r_i}{m_i}. \end{align*} $$
$$ \begin{align*} \left\lceil \frac{d_i\ell_i(x)}{m_i}\right\rceil-\frac{d_i\ell_i(x)}{m_i}&=\left\lceil \frac{q_im_i+r_i}{m_i}\right\rceil-\frac{q_im_i+r_i}{m_i}\\ &=q_i+\left\lceil\frac{r_i}{m_i}\right\rceil-\frac{r_i}{m_i}-q_i\\ &=1-\frac{r_i}{m_i}=\frac{m_i-r_i}{m_i}. \end{align*} $$
In other words, we have shown that
 $$ \begin{align*} \left\lceil \frac{d_i\ell_i(x)}{m_i}\right\rceil-\frac{d_i\ell_i(x)}{m_i}&=\begin{cases} 0, & d_i\ell_i(x)=0\quad\mod m_i, \\ -d_i\ell_i(x) \quad\mod m_i, & d_i\ell_i(x)\neq 0 \quad\mod m_i, \end{cases}\\ &= \frac{-d_i\ell_i(x) \quad\mod m_i}{m_i}=\frac{N_{m_i,d_i}(\operatorname{ord}_p(\ell_i(x)))}{m_i}. \end{align*} $$
$$ \begin{align*} \left\lceil \frac{d_i\ell_i(x)}{m_i}\right\rceil-\frac{d_i\ell_i(x)}{m_i}&=\begin{cases} 0, & d_i\ell_i(x)=0\quad\mod m_i, \\ -d_i\ell_i(x) \quad\mod m_i, & d_i\ell_i(x)\neq 0 \quad\mod m_i, \end{cases}\\ &= \frac{-d_i\ell_i(x) \quad\mod m_i}{m_i}=\frac{N_{m_i,d_i}(\operatorname{ord}_p(\ell_i(x)))}{m_i}. \end{align*} $$
Thus, the local discrepancies are given by
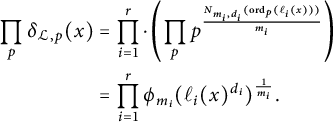 $$ \begin{align*} \prod_{p}\delta_{{\mathcal{L}},p}(x)&=\prod_{i=1}^r\cdot \left(\prod_p p^{\frac{N_{m_i,d_i}(\operatorname{ord}_p(\ell_i(x)))}{m_i}}\right)\\ &=\prod_{i=1}^r\phi_{m_i}(\ell_i(x)^{d_i})^{\frac{1}{m_i}}. \end{align*} $$
$$ \begin{align*} \prod_{p}\delta_{{\mathcal{L}},p}(x)&=\prod_{i=1}^r\cdot \left(\prod_p p^{\frac{N_{m_i,d_i}(\operatorname{ord}_p(\ell_i(x)))}{m_i}}\right)\\ &=\prod_{i=1}^r\phi_{m_i}(\ell_i(x)^{d_i})^{\frac{1}{m_i}}. \end{align*} $$
Combining equations 4.2–4.4 gives the desired conclusion.
Question 4.6 Consider a stacky curve
![]() $\mathfrak {X}=(X:(P_1,m_1), \ldots ,(P_r,m_r))$
. A line bundle M on X with a chosen height function
$\mathfrak {X}=(X:(P_1,m_1), \ldots ,(P_r,m_r))$
. A line bundle M on X with a chosen height function
![]() $H_M$
and integers
$H_M$
and integers
![]() $0\leq d_i<m_i$
. Then does
$0\leq d_i<m_i$
. Then does
 $$\begin{align*}H_{\mathcal{L}}(t)=H_M(t)\cdot \prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}(t)\cdot \prod_{i=1}^r \phi_{m_i}(\lambda(P_i,t)^{d_i})^{\frac{1}{m_i}}\end{align*}$$
$$\begin{align*}H_{\mathcal{L}}(t)=H_M(t)\cdot \prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}(t)\cdot \prod_{i=1}^r \phi_{m_i}(\lambda(P_i,t)^{d_i})^{\frac{1}{m_i}}\end{align*}$$
agree with the height constructed in [Reference Ellenberg, Satriano and Zureick-Brown6] up to a bounded constant when
![]() $X\neq {\mathbb {P}}^1_{\mathbb {Q}}$
. In other words, does our stacky height machine recover the heights in [Reference Ellenberg, Satriano and Zureick-Brown6] for all stacky curves over all number fields? If not, can one define different size functions
$X\neq {\mathbb {P}}^1_{\mathbb {Q}}$
. In other words, does our stacky height machine recover the heights in [Reference Ellenberg, Satriano and Zureick-Brown6] for all stacky curves over all number fields? If not, can one define different size functions
![]() $\tilde {N}_{m_i,d_i}\colon {\mathbb {Z}}_{\geq 0}\rightarrow {\mathbb {Z}}_{\geq 0}$
so that the ESZ-B height associated with
$\tilde {N}_{m_i,d_i}\colon {\mathbb {Z}}_{\geq 0}\rightarrow {\mathbb {Z}}_{\geq 0}$
so that the ESZ-B height associated with
![]() ${\mathcal {L}}$
is of the form
${\mathcal {L}}$
is of the form
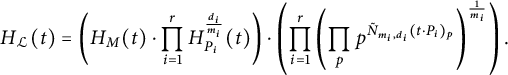 $$\begin{align*}H_{\mathcal{L}}(t)= \left(H_M(t)\cdot\prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}(t)\right)\cdot\left(\prod_{i=1}^r\left(\prod_p p^{\tilde{N}_{m_i,d_i}(t\cdot P_i)_p}\right)^{\frac{1}{m_i}}\right).\end{align*}$$
$$\begin{align*}H_{\mathcal{L}}(t)= \left(H_M(t)\cdot\prod_{i=1}^rH_{P_i}^{\frac{d_i}{m_i}}(t)\right)\cdot\left(\prod_{i=1}^r\left(\prod_p p^{\tilde{N}_{m_i,d_i}(t\cdot P_i)_p}\right)^{\frac{1}{m_i}}\right).\end{align*}$$
This result will follow provided one can show that the local degree of
![]() $\bar {x}^*{\mathcal {L}}$
with respect to
$\bar {x}^*{\mathcal {L}}$
with respect to
![]() $P_i$
over a prime p is
$P_i$
over a prime p is
 $$\begin{align*}\frac{d_i\operatorname{ord}_p(\lambda(P_i,t))}{m_i}=\frac{d_i(t\cdot P_i)_p}{m_i}.\end{align*}$$
$$\begin{align*}\frac{d_i\operatorname{ord}_p(\lambda(P_i,t))}{m_i}=\frac{d_i(t\cdot P_i)_p}{m_i}.\end{align*}$$
In this case, the argument given in Theorem 3.16 would give the desired result. Further, one might ask if these methods could be extended to compute the height functions of line bundles certain higher dimensional analogues of stacky curves.
4.2 Morphisms of stacky curves
We will require some results on morphisms between stacky curves.
Definition 4.7 (Darmon [Reference Darmon4])
Let
![]() $\mathfrak {X}_1=(X_1,(P,m_P)),\mathfrak {X}_2=(X_2,(Q,m_Q))$
be M curves defined over a number field K. A morphism of stacky curves over K is a morphism of algebraic curves
$\mathfrak {X}_1=(X_1,(P,m_P)),\mathfrak {X}_2=(X_2,(Q,m_Q))$
be M curves defined over a number field K. A morphism of stacky curves over K is a morphism of algebraic curves
![]() $\pi \colon X_1\rightarrow X_2$
defined over K such that for all
$\pi \colon X_1\rightarrow X_2$
defined over K such that for all
![]() $P\in X_1(K)$
with
$P\in X_1(K)$
with
![]() $\pi (P)=Q$
, we have that
$\pi (P)=Q$
, we have that
where
![]() $e_\pi (P)$
is the ramification index of
$e_\pi (P)$
is the ramification index of
![]() $\pi $
at P. We also define
$\pi $
at P. We also define
![]() $e_{\underline {\pi }}(P)=\frac {e_{\pi }(P)m_P}{m_{Q}}$
the ramification index of
$e_{\underline {\pi }}(P)=\frac {e_{\pi }(P)m_P}{m_{Q}}$
the ramification index of
![]() $\underline {\pi }$
at P.
$\underline {\pi }$
at P.
Now let
![]() $\mathfrak {X}=(X:{\mathbb {Q}};(P_1,m_1), \ldots ,(P_r,m_r))$
be an M curve. For any
$\mathfrak {X}=(X:{\mathbb {Q}};(P_1,m_1), \ldots ,(P_r,m_r))$
be an M curve. For any
![]() $s<r$
, choose positive divisors
$s<r$
, choose positive divisors
![]() $d_i$
of
$d_i$
of
![]() $m_i$
for
$m_i$
for
![]() $i=1,...,s$
. Then there is a multiplicity lowering morphism
$i=1,...,s$
. Then there is a multiplicity lowering morphism
defined by the identity morphism on X. The usefulness of this notion can be seen by the following.
Proposition 4.8 (Darmon [Reference Darmon4])
Let
![]() $\underline {\pi }\colon \mathfrak {X}_1\rightarrow \mathfrak {X}_2$
be a morphism of stacky curves defined over K. Then
$\underline {\pi }\colon \mathfrak {X}_1\rightarrow \mathfrak {X}_2$
be a morphism of stacky curves defined over K. Then
In other words, a morphism of stacky curves preserves the notion of S-integral points.
Lemma 4.9 Let K be a field and
 $$\begin{align*}U=\begin{bmatrix} 0 & 1\\ -1 &0 \end{bmatrix}.\end{align*}$$
$$\begin{align*}U=\begin{bmatrix} 0 & 1\\ -1 &0 \end{bmatrix}.\end{align*}$$
Define a bilinear form
![]() $L({\mathbf {v}},{\mathbf {x}})={\mathbf {v}}^TU^T{\mathbf {x}}$
. Let T be a non-singular matrix with entries in K. Then
$L({\mathbf {v}},{\mathbf {x}})={\mathbf {v}}^TU^T{\mathbf {x}}$
. Let T be a non-singular matrix with entries in K. Then
Proof We have that
Direct computation shows that
![]() $(UT)^TT=(\det T)U^T$
. We then have
$(UT)^TT=(\det T)U^T$
. We then have
Note that if
![]() $P=[a:b]$
and
$P=[a:b]$
and
![]() $t=[x,y]$
where
$t=[x,y]$
where
![]() $a,b$
and
$a,b$
and
![]() $x,y$
are coprime integers, then
$x,y$
are coprime integers, then
![]() $\lambda (P,t)=ay-bx$
by (4.1). In other words,
$\lambda (P,t)=ay-bx$
by (4.1). In other words,
![]() $\lambda (P,t)=L(P,t)$
as defined in (4.9).
$\lambda (P,t)=L(P,t)$
as defined in (4.9).
Lemma 4.10 Let
![]() $P=[a:b],t=[x,y]\in {\mathbb {P}}^1_{\mathbb {Q}}$
with
$P=[a:b],t=[x,y]\in {\mathbb {P}}^1_{\mathbb {Q}}$
with
![]() $a,b$
and
$a,b$
and
![]() $x,y$
coprime integers. Fix an integer
$x,y$
coprime integers. Fix an integer
![]() $m>1$
. Let
$m>1$
. Let
![]() $\alpha \colon {\mathbb {P}}^1_{\mathbb {Q}}\rightarrow {\mathbb {P}}^1_{\mathbb {Q}}$
be an automorphism. Let
$\alpha \colon {\mathbb {P}}^1_{\mathbb {Q}}\rightarrow {\mathbb {P}}^1_{\mathbb {Q}}$
be an automorphism. Let
![]() $\det \alpha $
be the smallest possible nonnegative determinant of an integral representation of
$\det \alpha $
be the smallest possible nonnegative determinant of an integral representation of
![]() $\alpha $
and similarly for
$\alpha $
and similarly for
![]() $\det \alpha ^{-1}$
. Then we have
$\det \alpha ^{-1}$
. Then we have
Proof Let L be as (4.1). Then we have that
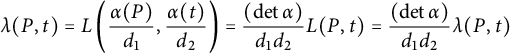 $$ \begin{align} \lambda(P,t)=L\left(\dfrac{\alpha(P)}{d_1},\dfrac{\alpha(t)}{d_2}\right)=\dfrac{(\det \alpha)}{d_1d_2}L(P,t)=\dfrac{(\det \alpha)}{d_1d_2}\lambda(P,t) \end{align} $$
$$ \begin{align} \lambda(P,t)=L\left(\dfrac{\alpha(P)}{d_1},\dfrac{\alpha(t)}{d_2}\right)=\dfrac{(\det \alpha)}{d_1d_2}L(P,t)=\dfrac{(\det \alpha)}{d_1d_2}\lambda(P,t) \end{align} $$
for some integers
![]() $d_1,d_2$
which account for common factors of
$d_1,d_2$
which account for common factors of
![]() $\alpha (P)$
and
$\alpha (P)$
and
![]() $\alpha (t)$
. Let
$\alpha (t)$
. Let
![]() $n_1=q_1m+r_1,n_2=q_2m+r_2$
be integers with
$n_1=q_1m+r_1,n_2=q_2m+r_2$
be integers with
![]() $0\leq r_i<m$
.
$0\leq r_i<m$
.
 $$ \begin{align} \phi_m(p^{n_1+n_2})= \begin{cases} p^{m-r_1-r_2}=\dfrac{\phi_m(p^{n_1})\phi_m(p^{n_2})}{p^m}, & \mathrm{if}\ r_1+r_2<m,\\ p^{m-(r_1+r_2-m)}=p^{2m-r_1-r_2}=\phi_m(p^{n_1})\phi_m(p^{n_2}), &\mathrm{if}\ r_1+r_2\geq m. \end{cases} \end{align} $$
$$ \begin{align} \phi_m(p^{n_1+n_2})= \begin{cases} p^{m-r_1-r_2}=\dfrac{\phi_m(p^{n_1})\phi_m(p^{n_2})}{p^m}, & \mathrm{if}\ r_1+r_2<m,\\ p^{m-(r_1+r_2-m)}=p^{2m-r_1-r_2}=\phi_m(p^{n_1})\phi_m(p^{n_2}), &\mathrm{if}\ r_1+r_2\geq m. \end{cases} \end{align} $$
Since
![]() $\phi _m$
is multiplicative, we have that
$\phi _m$
is multiplicative, we have that
![]() $\phi _m(zw)\leq \phi _m(z)\phi _m(w)\leq \operatorname {rad}_m(z)^{m-1}\phi _m(w)$
. Therefore, using (4.6),
$\phi _m(zw)\leq \phi _m(z)\phi _m(w)\leq \operatorname {rad}_m(z)^{m-1}\phi _m(w)$
. Therefore, using (4.6),
Applying the same reasoning using
![]() $\alpha ^{-1}$
, we have that
$\alpha ^{-1}$
, we have that
Therefore, we have
as required.
Corollary 4.11 Let
![]() $\mathfrak {X}=\mathfrak {X}({\mathbb {P}}^1;(P_1,m_1), \ldots ,(P_r,m_r))$
. Let
$\mathfrak {X}=\mathfrak {X}({\mathbb {P}}^1;(P_1,m_1), \ldots ,(P_r,m_r))$
. Let
![]() $\alpha \colon {\mathbb {P}}^1_{\mathbb {Q}}\rightarrow {\mathbb {P}}^1_{\mathbb {Q}}$
be an automorphism of
$\alpha \colon {\mathbb {P}}^1_{\mathbb {Q}}\rightarrow {\mathbb {P}}^1_{\mathbb {Q}}$
be an automorphism of
![]() ${\mathbb {P}}^1_{\mathbb {Q}}$
. Let
${\mathbb {P}}^1_{\mathbb {Q}}$
. Let
![]() $Q_i=\alpha (P_i)$
and
$Q_i=\alpha (P_i)$
and
![]() $\mathfrak {Y}=\mathfrak {Y}({\mathbb {P}}^1;(Q_1,m_1), \ldots ,(Q_r,m_r))$
. Then
$\mathfrak {Y}=\mathfrak {Y}({\mathbb {P}}^1;(Q_1,m_1), \ldots ,(Q_r,m_r))$
. Then
![]() $\alpha $
induces an isomorphism
$\alpha $
induces an isomorphism
![]() $\underline {\alpha }\colon \mathfrak {X}\rightarrow \mathfrak {Y}$
. Let
$\underline {\alpha }\colon \mathfrak {X}\rightarrow \mathfrak {Y}$
. Let
![]() $\det \alpha $
and
$\det \alpha $
and
![]() $\det \alpha ^{-1}$
be as in (4.10). Let
$\det \alpha ^{-1}$
be as in (4.10). Let
![]() $D(\alpha ,\mathfrak {X})=\prod _{i=1}^r\operatorname {rad}_{m_i}(\det \alpha )^{1-1/m_i}$
and similarly define
$D(\alpha ,\mathfrak {X})=\prod _{i=1}^r\operatorname {rad}_{m_i}(\det \alpha )^{1-1/m_i}$
and similarly define
![]() $D(\alpha ^{-1},\mathfrak {X})$
. Suppose that
$D(\alpha ^{-1},\mathfrak {X})$
. Suppose that
![]() $C_\phi $
is a constant (such a constant always exists) such that
$C_\phi $
is a constant (such a constant always exists) such that
Then
Proof By assumption, for each
![]() $i=1, \ldots ,r$
, we have from (4.10) and our assumption that
$i=1, \ldots ,r$
, we have from (4.10) and our assumption that
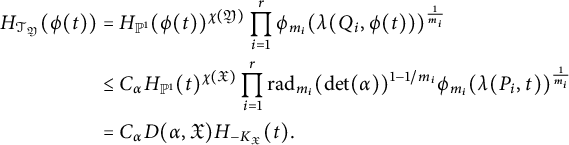 $$ \begin{align*} H_{{\mathcal{T}}_{\mathfrak{Y}}}(\phi(t))&=H_{{\mathbb{P}}^1}(\phi(t))^{\chi( \mathfrak{Y})}\prod_{i=1}^r\phi_{m_i}(\lambda(Q_i,\phi(t)))^{\frac{1}{m_i}}\\ &\leq C_\alpha H_{{\mathbb{P}}^1}(t)^{\chi(\mathfrak{X})}\prod_{i=1}^r\operatorname{rad}_{m_i}(\det(\alpha))^{1-1/m_i}\phi_{m_i}(\lambda(P_i,t))^{\frac{1}{m_i}}\\&=C_\alpha D(\alpha,\mathfrak{X})H_{-K_{\mathfrak{X}}}(t). \end{align*} $$
$$ \begin{align*} H_{{\mathcal{T}}_{\mathfrak{Y}}}(\phi(t))&=H_{{\mathbb{P}}^1}(\phi(t))^{\chi( \mathfrak{Y})}\prod_{i=1}^r\phi_{m_i}(\lambda(Q_i,\phi(t)))^{\frac{1}{m_i}}\\ &\leq C_\alpha H_{{\mathbb{P}}^1}(t)^{\chi(\mathfrak{X})}\prod_{i=1}^r\operatorname{rad}_{m_i}(\det(\alpha))^{1-1/m_i}\phi_{m_i}(\lambda(P_i,t))^{\frac{1}{m_i}}\\&=C_\alpha D(\alpha,\mathfrak{X})H_{-K_{\mathfrak{X}}}(t). \end{align*} $$
Similarly, we have
 $$ \begin{align*} H_{{\mathcal{T}}_{\mathfrak{Y}}}(\phi(t))&=H_{{\mathbb{P}}^1}(\phi(t))^{\chi( \mathfrak{Y})}\prod_{i=1}^r\phi_{m_i}(\lambda(Q_i,\phi(t)))^{\frac{1}{m_i}}\\&\geq C_\alpha^{-1} H_{{\mathbb{P}}^1}(t)^{\chi(\mathfrak{X})}\prod_{i=1}^r\operatorname{rad}_{m_i}(\det(\alpha^{-1}))^{-(1-1/m_i)}\phi_{m_i}(\lambda(P_i,t))^{\frac{1}{m_i}}\\&=C_\alpha^{-1} D(\alpha^{-1},\mathfrak{X})H_{-K_{\mathfrak{X}}}(t).\\[-37pt] \end{align*} $$
$$ \begin{align*} H_{{\mathcal{T}}_{\mathfrak{Y}}}(\phi(t))&=H_{{\mathbb{P}}^1}(\phi(t))^{\chi( \mathfrak{Y})}\prod_{i=1}^r\phi_{m_i}(\lambda(Q_i,\phi(t)))^{\frac{1}{m_i}}\\&\geq C_\alpha^{-1} H_{{\mathbb{P}}^1}(t)^{\chi(\mathfrak{X})}\prod_{i=1}^r\operatorname{rad}_{m_i}(\det(\alpha^{-1}))^{-(1-1/m_i)}\phi_{m_i}(\lambda(P_i,t))^{\frac{1}{m_i}}\\&=C_\alpha^{-1} D(\alpha^{-1},\mathfrak{X})H_{-K_{\mathfrak{X}}}(t).\\[-37pt] \end{align*} $$
We can get slightly worse, but more understandable bounds as follows. We always have
![]() $\operatorname {rad}_m(x)\leq \operatorname {rad}(x)$
. Note that we have that
$\operatorname {rad}_m(x)\leq \operatorname {rad}(x)$
. Note that we have that
![]() $\sum _{i=1}^r(1-1/m_i)=2-\chi (\mathfrak {X})=2g(\mathfrak {X})$
. Thus, we in fact have
$\sum _{i=1}^r(1-1/m_i)=2-\chi (\mathfrak {X})=2g(\mathfrak {X})$
. Thus, we in fact have
Of particular note is that we see that when studying the Northcott property, we may change the height by an automorphism. Thus, the Northcott property is stable under isomorphism as expected.
4.3 Northcott property of the canonical height on stacky curves
We now investigate the properties of the canonical height on stacky curves, given by
 $$ \begin{align} H_{({\mathbf{a}}, {\mathbf{m}})}(x,y) = \prod_{i=1}^n r_{m_i} (\ell_i(x,y))^{\frac{1}{m_i}} \cdot \max\{|x|, |y|\}^{-\delta({\mathbf{m}})}. \end{align} $$
$$ \begin{align} H_{({\mathbf{a}}, {\mathbf{m}})}(x,y) = \prod_{i=1}^n r_{m_i} (\ell_i(x,y))^{\frac{1}{m_i}} \cdot \max\{|x|, |y|\}^{-\delta({\mathbf{m}})}. \end{align} $$
When
![]() $\delta ({\mathbf {m}}) = 0$
, we see that the canonical height exhibits a clear duality with the anti-canonical height, and so the same argument shows that Northcott’s property will fail. When
$\delta ({\mathbf {m}}) = 0$
, we see that the canonical height exhibits a clear duality with the anti-canonical height, and so the same argument shows that Northcott’s property will fail. When
![]() $\delta ({\mathbf {m}}) < 0$
, we then see at once that
$\delta ({\mathbf {m}}) < 0$
, we then see at once that
![]() $H_{({\mathbf {a}}, {\mathbf {m}})}$
will have Northcott’s property as a consequence that the Weil height having Northcott’s property. It remains to consider Northcott’s property when
$H_{({\mathbf {a}}, {\mathbf {m}})}$
will have Northcott’s property as a consequence that the Weil height having Northcott’s property. It remains to consider Northcott’s property when
![]() $\delta ({\mathbf {m}})> 0$
. In this case, we have
$\delta ({\mathbf {m}})> 0$
. In this case, we have
![]() ${\mathbf {m}} = (2, m_2, m_3)$
with
${\mathbf {m}} = (2, m_2, m_3)$
with
It suffices to show that for any such pair
![]() $(m_2,m_3)$
, there exist integers
$(m_2,m_3)$
, there exist integers
![]() $a,b,c$
such that the curve
$a,b,c$
such that the curve
has infinitely many primitive integral solutions. This is the content of Beukers’ paper [Reference Beukers1], and we are done.
5 On the Northcott property of canonical and anti-canonical heights on stacky curves
In this section, we prove Theorem 1.2, starting with Theorem 2.1. We start with a reduction procedure of a curve
![]() $\mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}, {\mathbf {m}}))$
which we describe colloquially. By convention, we shall take our weight vectors
$\mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}, {\mathbf {m}}))$
which we describe colloquially. By convention, we shall take our weight vectors
![]() ${\mathbf {m}}$
to have the property that
${\mathbf {m}}$
to have the property that
Definition 5.1 Consider a stacky curve
![]() $\mathfrak {X}(X : ({\mathbf {a}}, {\mathbf {m}}))$
with
$\mathfrak {X}(X : ({\mathbf {a}}, {\mathbf {m}}))$
with
![]() ${\mathbf {a}}=(P_1, \ldots ,P_r)$
. Let
${\mathbf {a}}=(P_1, \ldots ,P_r)$
. Let
![]() ${\mathbf {i}}=i_1, \ldots ,i_k$
be a sub-sequence of
${\mathbf {i}}=i_1, \ldots ,i_k$
be a sub-sequence of
![]() $1,2,...,r$
. Then there is a morphism
$1,2,...,r$
. Then there is a morphism
![]() $\pi _{{\mathbf {i}}}\colon \mathfrak {X}(X : ({\mathbf {a}}, {\mathbf {m}}))\rightarrow \mathfrak {X}(X : ({\mathbf {a}}^\prime , {\mathbf {m}}^\prime ))$
where
$\pi _{{\mathbf {i}}}\colon \mathfrak {X}(X : ({\mathbf {a}}, {\mathbf {m}}))\rightarrow \mathfrak {X}(X : ({\mathbf {a}}^\prime , {\mathbf {m}}^\prime ))$
where
![]() ${\mathbf {a}}^\prime =(P_{i_1}, \ldots ,P_{i_k})$
and
${\mathbf {a}}^\prime =(P_{i_1}, \ldots ,P_{i_k})$
and
![]() ${\mathbf {m}}^\prime =(m_{i_1},\ldots ,m_{i_k})$
. The map is defined by taking the identity morphism on the coarse space X. We call such a morphism a totally ramified canonical covering.
${\mathbf {m}}^\prime =(m_{i_1},\ldots ,m_{i_k})$
. The map is defined by taking the identity morphism on the coarse space X. We call such a morphism a totally ramified canonical covering.
The above construction defines a morphism by the definition of a morphism of M-curves. It is totally ramified in the sense that if i is some index that does not appear in
![]() ${\mathbf {i}}$
, then
${\mathbf {i}}$
, then
![]() $\pi _{\mathbf {i}}$
has ramification index
$\pi _{\mathbf {i}}$
has ramification index
![]() $m_i$
at
$m_i$
at
![]() $P_i$
. We use the term canonical this type of construction can be used for any stacky curve. In particular, by taking
$P_i$
. We use the term canonical this type of construction can be used for any stacky curve. In particular, by taking
![]() ${\mathbf {i}}$
to be the empty set, we obtain the coarse space morphism. We will show that if Theorem 2.1 holds for a totally ramified canonical covering of the shape
${\mathbf {i}}$
to be the empty set, we obtain the coarse space morphism. We will show that if Theorem 2.1 holds for a totally ramified canonical covering of the shape
![]() $\mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}^\prime , {\mathbf {m}}^\prime ))$
where
$\mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}^\prime , {\mathbf {m}}^\prime ))$
where
![]() ${\mathbf {a}}^\prime , {\mathbf {m}}^\prime $
is obtained from
${\mathbf {a}}^\prime , {\mathbf {m}}^\prime $
is obtained from
![]() ${\mathbf {a}}, {\mathbf {m}}$
, respectively, by removing a subset of indices, then it also holds for
${\mathbf {a}}, {\mathbf {m}}$
, respectively, by removing a subset of indices, then it also holds for
![]() $\mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}, {\mathbf {m}}))$
(see Theorem 5.2 below).
$\mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}, {\mathbf {m}}))$
(see Theorem 5.2 below).
Theorem 5.2 Let
![]() $\mathfrak {X}({\mathbb {P}}^1 : (a_1, m_1), \ldots , (a_n, m_n))$
be a stacky curve. If the Northcott property fails for the height (2.2) for some totally ramified canonical cover of
$\mathfrak {X}({\mathbb {P}}^1 : (a_1, m_1), \ldots , (a_n, m_n))$
be a stacky curve. If the Northcott property fails for the height (2.2) for some totally ramified canonical cover of
![]() $\mathfrak {X}$
, then it will also fail for
$\mathfrak {X}$
, then it will also fail for
![]() $\mathfrak {X}$
.
$\mathfrak {X}$
.
Proof Let
![]() $\mathfrak {X}$
be given as in the statement of Theorem 5.2. We may assume, after reindexing the points if necessary, that the Northcott property for the ESZ-B height fails for the totally ramified canonical cover given by
$\mathfrak {X}$
be given as in the statement of Theorem 5.2. We may assume, after reindexing the points if necessary, that the Northcott property for the ESZ-B height fails for the totally ramified canonical cover given by
for some
![]() $k \leq n$
. This implies that, for some positive number
$k \leq n$
. This implies that, for some positive number
![]() $C_k$
depending at most on
$C_k$
depending at most on
![]() $a_1, \ldots , a_k$
and
$a_1, \ldots , a_k$
and
![]() $m_1, \ldots , m_k$
, there are infinitely many integers
$m_1, \ldots , m_k$
, there are infinitely many integers
![]() $x,y$
such that
$x,y$
such that
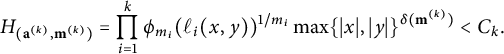 $$\begin{align*}H_{({\mathbf{a}}^{(k)}, {\mathbf{m}}^{(k)})} = \prod_{i=1}^k \phi_{m_i} (\ell_i(x,y))^{1/m_i} \max\{|x|, |y|\}^{\delta({\mathbf{m}}^{(k)})} < C_k.\end{align*}$$
$$\begin{align*}H_{({\mathbf{a}}^{(k)}, {\mathbf{m}}^{(k)})} = \prod_{i=1}^k \phi_{m_i} (\ell_i(x,y))^{1/m_i} \max\{|x|, |y|\}^{\delta({\mathbf{m}}^{(k)})} < C_k.\end{align*}$$
Next, note that the quotient
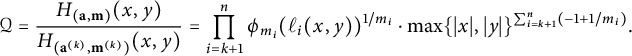 $$\begin{align*}{\mathcal{Q}} = \frac{H_{({\mathbf{a}}, {\mathbf{m}})}(x,y)}{H_{({\mathbf{a}}^{(k)}, {\mathbf{m}}^{(k)})}(x,y)} = \prod_{i={k+1}}^n \phi_{m_i}(\ell_i(x,y))^{1/m_i} \cdot \max\{|x|, |y|\}^{\sum_{i=k+1}^n (-1 + 1/m_i)}. \end{align*}$$
$$\begin{align*}{\mathcal{Q}} = \frac{H_{({\mathbf{a}}, {\mathbf{m}})}(x,y)}{H_{({\mathbf{a}}^{(k)}, {\mathbf{m}}^{(k)})}(x,y)} = \prod_{i={k+1}}^n \phi_{m_i}(\ell_i(x,y))^{1/m_i} \cdot \max\{|x|, |y|\}^{\sum_{i=k+1}^n (-1 + 1/m_i)}. \end{align*}$$
Observe that
![]() $\phi _m(s) \leq |s|^{m-1}$
for any integer s, with equality if and only if s is square-free. It follows that
$\phi _m(s) \leq |s|^{m-1}$
for any integer s, with equality if and only if s is square-free. It follows that
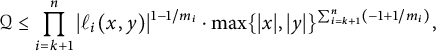 $$\begin{align*}{\mathcal{Q}} \leq \prod_{i=k+1}^n |\ell_i(x,y)|^{1 - 1/m_i} \cdot \max\{|x|, |y|\}^{\sum_{i=k+1}^n (-1 + 1/m_i)},\end{align*}$$
$$\begin{align*}{\mathcal{Q}} \leq \prod_{i=k+1}^n |\ell_i(x,y)|^{1 - 1/m_i} \cdot \max\{|x|, |y|\}^{\sum_{i=k+1}^n (-1 + 1/m_i)},\end{align*}$$
and from here we immediately see from the triangle inequality that
Thus, by replacing
![]() $C_k$
with a larger positive number if necessary, we see that the Northcott property also fails for
$C_k$
with a larger positive number if necessary, we see that the Northcott property also fails for
![]() $H_{({\mathbf {a}}, {\mathbf {m}})}$
on
$H_{({\mathbf {a}}, {\mathbf {m}})}$
on
![]() $\mathfrak {X}$
.
$\mathfrak {X}$
.
Now, given Theorem 5.2, it remains to consider certain minimal choices of
![]() ${\mathbf {m}}$
. We say that
${\mathbf {m}}$
. We say that
![]() $\delta ({\mathbf {m}})$
is minimally nonnegative if there is no subsequence
$\delta ({\mathbf {m}})$
is minimally nonnegative if there is no subsequence
![]() ${\mathbf {m}}^\prime $
of
${\mathbf {m}}^\prime $
of
![]() ${\mathbf {m}}$
such that
${\mathbf {m}}$
such that
![]() $\delta ({\mathbf {m}}^\prime ) \leq 0$
. We have the following lemma characterizing the minimally nonnegative tuples.
$\delta ({\mathbf {m}}^\prime ) \leq 0$
. We have the following lemma characterizing the minimally nonnegative tuples.
Lemma 5.3 Suppose
![]() ${\mathbf {m}} = (m_1, \ldots , m_n)$
with
${\mathbf {m}} = (m_1, \ldots , m_n)$
with
![]() $2 \leq m_1 \leq \cdots \leq m_n$
is minimally nonnegative. Then
$2 \leq m_1 \leq \cdots \leq m_n$
is minimally nonnegative. Then
![]() $n \leq 4$
.
$n \leq 4$
.
Proof Suppose
![]() $n \geq 5$
. If there exist
$n \geq 5$
. If there exist
![]() $m_i, m_j, m_k \geq 3$
, then the sub-sequence
$m_i, m_j, m_k \geq 3$
, then the sub-sequence
![]() $(m_i, m_j, m_k)$
satisfies
$(m_i, m_j, m_k)$
satisfies
![]() $\delta ((m_i, m_j, m_k)) \leq 0$
, so
$\delta ((m_i, m_j, m_k)) \leq 0$
, so
![]() ${\mathbf {m}}$
is not minimally nonnegative. If
${\mathbf {m}}$
is not minimally nonnegative. If
![]() $m_3 \geq 3$
, then such a choice of
$m_3 \geq 3$
, then such a choice of
![]() $i,j,k$
exists, since
$i,j,k$
exists, since
![]() $n \geq 5$
. Therefore, we may assume that
$n \geq 5$
. Therefore, we may assume that
![]() $m_1 = m_2 = m_3 = 2$
. But then,
$m_1 = m_2 = m_3 = 2$
. But then,
![]() $(2,2,2,m_4)$
satisfies
$(2,2,2,m_4)$
satisfies
![]() $\delta ((2,2,2,m_4)) \leq 0$
, so
$\delta ((2,2,2,m_4)) \leq 0$
, so
![]() ${\mathbf {m}}$
is not minimally nonnegative.
${\mathbf {m}}$
is not minimally nonnegative.
It remains to deal with minimally nonnegative tuples with
![]() $n = 3,4$
. Before we proceed, we will require Theorem 2.2, which we prove now.
$n = 3,4$
. Before we proceed, we will require Theorem 2.2, which we prove now.
Proof of Theorem 2.2
As we remarked earlier, the proof given here is provided to us by Shnidman in [Reference Shnidman15].
For given non-singular binary quartic form
![]() $F \in {\mathbb {Z}}[x,y]$
given by
$F \in {\mathbb {Z}}[x,y]$
given by
we write
![]() $C_F$
for the curve defined by
$C_F$
for the curve defined by
The Jacobian of the genus one curve
![]() $C_{a,b}$
is the elliptic curve
$C_{a,b}$
is the elliptic curve
![]() $E_{a,b}$
given by
$E_{a,b}$
given by
where
![]() $I,J$
are the basic invariants given by
$I,J$
are the basic invariants given by
By 2-descent, we see that
![]() $C_{F}$
corresponds to a class c in
$C_{F}$
corresponds to a class c in
![]() $H^1({\mathbb {Q}} , E_{a,b}[2])$
. Note that for any integer d, the group
$H^1({\mathbb {Q}} , E_{a,b}[2])$
. Note that for any integer d, the group
![]() $H^1({\mathbb {Q}}, E_{F}^{(d)}[2])$
is canonically isomorphic to
$H^1({\mathbb {Q}}, E_{F}^{(d)}[2])$
is canonically isomorphic to
![]() $H^1({\mathbb {Q}} , E_{F}^{(d)}[2])$
such that c is the class of
$H^1({\mathbb {Q}} , E_{F}^{(d)}[2])$
such that c is the class of
![]() $C_{F}^{(d)}$
in
$C_{F}^{(d)}$
in
![]() $H^1({\mathbb {Q}}, E_{F}^{(d)}[2])$
.
$H^1({\mathbb {Q}}, E_{F}^{(d)}[2])$
.
We now consider two cases. First suppose that c does not come from 2-torsion. In this case, it is immediate that
![]() $E_{F}^{(d_0)}$
has positive rank, where
$E_{F}^{(d_0)}$
has positive rank, where
This is because in this case
![]() $C_{F}^{(d_0)}({\mathbb {Q}}) \ne \emptyset $
.
$C_{F}^{(d_0)}({\mathbb {Q}}) \ne \emptyset $
.
If c comes from 2-torsion, then we note that
![]() $C_{F}^{(d)}({\mathbb {Q}})$
is non-empty for all
$C_{F}^{(d)}({\mathbb {Q}})$
is non-empty for all
![]() $d \in {\mathbb {Z}}$
. That is, for all
$d \in {\mathbb {Z}}$
. That is, for all
![]() $d \in {\mathbb {Z}}$
, we have
$d \in {\mathbb {Z}}$
, we have
![]() $C_{F}^{(d)}$
is isomorphic to
$C_{F}^{(d)}$
is isomorphic to
![]() $E_{F}^{(d)}$
over
$E_{F}^{(d)}$
over
![]() ${\mathbb {Q}}$
. We can then choose a class
${\mathbb {Q}}$
. We can then choose a class
![]() $c^\prime $
in
$c^\prime $
in
![]() $H^1({\mathbb {Q}}, E_{F}[2])$
, represented by a different binary quartic form G, and choose d such that the twist of the genus one curve
$H^1({\mathbb {Q}}, E_{F}[2])$
, represented by a different binary quartic form G, and choose d such that the twist of the genus one curve
![]() ${\mathcal {C}} : z^2 = G(u,v)$
given by
${\mathcal {C}} : z^2 = G(u,v)$
given by
![]() ${\mathcal {C}}^{(d)}$
has a rational point. This implies that
${\mathcal {C}}^{(d)}$
has a rational point. This implies that
![]() $E_{F}^{(d)}$
has positive rank. Then, with this choice of d, we find that
$E_{F}^{(d)}$
has positive rank. Then, with this choice of d, we find that
![]() $C_{F}^{(d)}({\mathbb {Q}}) \ne \emptyset $
and
$C_{F}^{(d)}({\mathbb {Q}}) \ne \emptyset $
and
![]() $E_{F}^{(d)}$
has positive rank, which completes the proof.
$E_{F}^{(d)}$
has positive rank, which completes the proof.
With Theorem 2.2, we proceed to handle minimally nonnegative tuples, starting with the case
![]() $n = 4$
.
$n = 4$
.
5.1 Minimally nonnegative tuples with
 $n = 4$
$n = 4$
We begin with the case
![]() ${\mathbf {m}} = (2,2,2,2)$
, and we will need Theorem 2.2. By
${\mathbf {m}} = (2,2,2,2)$
, and we will need Theorem 2.2. By
![]() $3$
-transivity of the action of
$3$
-transivity of the action of
![]() $\operatorname {PGL}_2$
on
$\operatorname {PGL}_2$
on
![]() ${\mathbb {P}}^1$
and Lemma 4.10, we may assume that three of the points are
${\mathbb {P}}^1$
and Lemma 4.10, we may assume that three of the points are
![]() $0, 1, \infty $
, corresponding to the linear forms
$0, 1, \infty $
, corresponding to the linear forms
![]() $x,y, x+y$
in the variables
$x,y, x+y$
in the variables
![]() $x,y$
. We then write
$x,y$
. We then write
![]() $\ell (x,y) = ax + by$
for the linear form representing the fourth half-point.
$\ell (x,y) = ax + by$
for the linear form representing the fourth half-point.
We prove the following as a warm-up.
Lemma 5.4 There exist integers
![]() $a,b$
such that the stack
$a,b$
such that the stack
![]() $\mathfrak {X}({\mathbb {P}}_{\mathbb {Q}}^1: (0, 2), (1, 2), (\infty , 2), (a/b, 2))$
has infinitely many rational points of E-S-ZB height equal to one.
$\mathfrak {X}({\mathbb {P}}_{\mathbb {Q}}^1: (0, 2), (1, 2), (\infty , 2), (a/b, 2))$
has infinitely many rational points of E-S-ZB height equal to one.
Proof In this case, the height is given by
so this is equal to one if and only if each of
![]() $x, y, x+y, ax+by$
is a square. To wit, we set
$x, y, x+y, ax+by$
is a square. To wit, we set
This induces the equation
which is solvable and whose (primitive) integral solutions are parametrized by
Inserting this into
![]() $ax + by$
gives
$ax + by$
gives
We then fix
![]() $u = u_0, v = v_0$
so that
$u = u_0, v = v_0$
so that
![]() $2u_0 v_0$
and
$2u_0 v_0$
and
![]() $u_0^2 - v_0^2$
are co-prime, then solve the linear diophantine equation
$u_0^2 - v_0^2$
are co-prime, then solve the linear diophantine equation
Given a solution
![]() $(a,b)$
to this diophantine equation, one obtains a genus curve defined by
$(a,b)$
to this diophantine equation, one obtains a genus curve defined by
which is isomorphic to an elliptic curve, since it has a rational point given by
![]() $w_0^2 = F_{a,b}(u_0, v_0)$
. In particular, it must be isomorphic to its Jacobian. A simple calculation shows that the Jacobian of this genus one curve is given by the equation
$w_0^2 = F_{a,b}(u_0, v_0)$
. In particular, it must be isomorphic to its Jacobian. A simple calculation shows that the Jacobian of this genus one curve is given by the equation
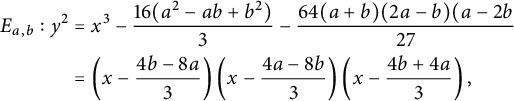 $$ \begin{align} E_{a,b} : y^2 &= x^3 - \frac{16(a^2 - ab + b^2)}{3} - \frac{64(a+b)(2a-b)(a-2b}{27}\\&= \left( x - \frac{4b - 8a}{3}\right)\left( x - \frac{4a - 8b}{3}\right)\left( x - \frac{4b + 4a}{3}\right), \nonumber \end{align} $$
$$ \begin{align} E_{a,b} : y^2 &= x^3 - \frac{16(a^2 - ab + b^2)}{3} - \frac{64(a+b)(2a-b)(a-2b}{27}\\&= \left( x - \frac{4b - 8a}{3}\right)\left( x - \frac{4a - 8b}{3}\right)\left( x - \frac{4b + 4a}{3}\right), \nonumber \end{align} $$
so it suffices to find
![]() $a,b$
such that
$a,b$
such that
![]() $E_{a,b}$
has positive rank. We find that setting
$E_{a,b}$
has positive rank. We find that setting
![]() $u_0 = 1, v_0 = 5$
and
$u_0 = 1, v_0 = 5$
and
![]() $a = 17, b = -118$
that the curve
$a = 17, b = -118$
that the curve
![]() $E_{a,b}$
has positive rank, and therefore
$E_{a,b}$
has positive rank, and therefore
![]() $w^2 = F_{a,b}(u,v)$
will have infinitely many integral solutions
$w^2 = F_{a,b}(u,v)$
will have infinitely many integral solutions
![]() $(u,v,w)$
. This gives infinitely many pairs
$(u,v,w)$
. This gives infinitely many pairs
![]() $u,v$
such that
$u,v$
such that
![]() $F_{17,-118}(u,v)$
is a square. This implies our result, since
$F_{17,-118}(u,v)$
is a square. This implies our result, since
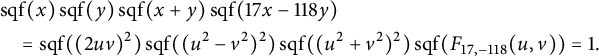 $$\begin{align*}&\operatorname{sqf}(x) \operatorname{sqf}(y) \operatorname{sqf}(x+y) \operatorname{sqf}(17x-118y)\\& \quad = \operatorname{sqf}((2uv)^2) \operatorname{sqf}((u^2 - v^2)^2) \operatorname{sqf}((u^2 + v^2)^2) \operatorname{sqf}(F_{17,-118}(u,v)) = 1.\\[-34pt] \end{align*}$$
$$\begin{align*}&\operatorname{sqf}(x) \operatorname{sqf}(y) \operatorname{sqf}(x+y) \operatorname{sqf}(17x-118y)\\& \quad = \operatorname{sqf}((2uv)^2) \operatorname{sqf}((u^2 - v^2)^2) \operatorname{sqf}((u^2 + v^2)^2) \operatorname{sqf}(F_{17,-118}(u,v)) = 1.\\[-34pt] \end{align*}$$
The general case will follow by applying the same ideas in tandem with Theorem 2.2. Indeed, Theorem 2.2 gives that for any
![]() $a,b \in {\mathbb {Z}}$
such that
$a,b \in {\mathbb {Z}}$
such that
![]() $F_{a,b}(u,v) = a(u^2 - v^2)^2 + 4bu^2 v^2$
is non-singular that there exists
$F_{a,b}(u,v) = a(u^2 - v^2)^2 + 4bu^2 v^2$
is non-singular that there exists
![]() $d \in {\mathbb {Z}}$
such that
$d \in {\mathbb {Z}}$
such that
![]() $C_F({\mathbb {Q}}) \ne \emptyset $
and
$C_F({\mathbb {Q}}) \ne \emptyset $
and
![]() $E_F$
has positive rank. Fixing such a d, we see that there are infinitely many co-prime integers
$E_F$
has positive rank. Fixing such a d, we see that there are infinitely many co-prime integers
![]() $u,v,z$
such that
$u,v,z$
such that
Recall that in this setup we have
whence
This concludes the proof for the
![]() ${\mathbf {m}} = (2,2,2,2)$
case.
${\mathbf {m}} = (2,2,2,2)$
case.
Note that if
![]() ${\mathbf {m}} = (m_1, m_2, m_3, m_4)$
is minimally nonnegative, then
${\mathbf {m}} = (m_1, m_2, m_3, m_4)$
is minimally nonnegative, then
![]() $m_1 = m_2 = 2$
, since
$m_1 = m_2 = 2$
, since
![]() $\delta ((3,3,3)) = 0$
. Thus, we may write
$\delta ((3,3,3)) = 0$
. Thus, we may write
with
![]() $x_1, y_1$
square-free. We then write
$x_1, y_1$
square-free. We then write
Again, we have
![]() $z_i, w_j$
are square-free for
$z_i, w_j$
are square-free for
![]() $1 \leq i \leq m_3 - 1$
and
$1 \leq i \leq m_3 - 1$
and
![]() $1 \leq j \leq m_4 - 1$
.
$1 \leq j \leq m_4 - 1$
.
We now specialize to the points where
![]() $z_i = w_j = 1$
except for
$z_i = w_j = 1$
except for
![]() $i = 2$
and
$i = 2$
and
![]() $j = 1,2$
, as well as
$j = 1,2$
, as well as
![]() $x_1 = y_1 = 1$
. Applying Theorem 2.2 and using the same argument as in the
$x_1 = y_1 = 1$
. Applying Theorem 2.2 and using the same argument as in the
![]() $(2,2,2,2)$
case, we see that there is a choice of
$(2,2,2,2)$
case, we see that there is a choice of
![]() $w_1 = d$
such that there are infinitely many choices of
$w_1 = d$
such that there are infinitely many choices of
![]() $x_2, y_2, w_2, z_2$
satisfying
$x_2, y_2, w_2, z_2$
satisfying
The height of such a point is given by
It follows that there are infinitely many points of bounded height, and so Northcott’s property fails.
5.2 Minimally nonnegative tuples with
 $n = 3$
$n = 3$
To complete the proof of Theorem 2.1, it remains to handle the cases when
![]() $n = 3$
and
$n = 3$
and
![]() $\chi (\mathfrak {X}) \leq 0$
. We shall assume that
$\chi (\mathfrak {X}) \leq 0$
. We shall assume that
![]() $m_1 \leq m_2 \leq m_3$
. We then note that
$m_1 \leq m_2 \leq m_3$
. We then note that
![]() $\delta ({\mathbf {m}}) \leq 0$
if and only if one of the following conditions is satisfied:
$\delta ({\mathbf {m}}) \leq 0$
if and only if one of the following conditions is satisfied:
-
(1)
 $m_1 \geq 3$
.
$m_1 \geq 3$
. -
(2)
 $m_1 = 2, m_2 = 3, m_3 \geq 6$
.
$m_1 = 2, m_2 = 3, m_3 \geq 6$
. -
(3)
 $m_1 = 2, m_2 \geq 4$
.
$m_1 = 2, m_2 \geq 4$
.
We deal with the first case. We then write
Now set
and
Then the value of the height
![]() $H_{({\mathbf {a}}, {\mathbf {m}})}(x,y)$
in this case is given by
$H_{({\mathbf {a}}, {\mathbf {m}})}(x,y)$
in this case is given by
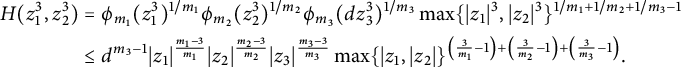 $$ \begin{align*} H(z_1^3, z_2^3) & = \phi_{m_1}(z_1^3)^{1/m_1} \phi_{m_2}(z_2^3)^{1/m_2} \phi_{m_3}(d z_3^3)^{1/m_3} \max\{|z_1|^3, |z_2|^3\}^{1/m_1 + 1/m_2 + 1/m_3 - 1} \\ & \leq d^{m_3 - 1} |z_1|^{\frac{m_1 - 3}{m_1}} |z_2|^{\frac{m_2 - 3}{m_2}} |z_3|^{\frac{m_3 - 3}{m_3}} \max\{|z_1, |z_2|\}^{\left(\frac{3}{m_1} - 1 \right) + \left(\frac{3}{m_2} - 1 \right) + \left(\frac{3}{m_3} - 1 \right)}. \end{align*} $$
$$ \begin{align*} H(z_1^3, z_2^3) & = \phi_{m_1}(z_1^3)^{1/m_1} \phi_{m_2}(z_2^3)^{1/m_2} \phi_{m_3}(d z_3^3)^{1/m_3} \max\{|z_1|^3, |z_2|^3\}^{1/m_1 + 1/m_2 + 1/m_3 - 1} \\ & \leq d^{m_3 - 1} |z_1|^{\frac{m_1 - 3}{m_1}} |z_2|^{\frac{m_2 - 3}{m_2}} |z_3|^{\frac{m_3 - 3}{m_3}} \max\{|z_1, |z_2|\}^{\left(\frac{3}{m_1} - 1 \right) + \left(\frac{3}{m_2} - 1 \right) + \left(\frac{3}{m_3} - 1 \right)}. \end{align*} $$
Observe that
for
![]() $i = 1,2,3$
.
$i = 1,2,3$
.
It remains to choose d so that the plane cubic curve
has infinitely many rational points. This is an easy consequence of the seminal work of Stewart and Top [Reference Stewart and Top18, Theorem 7], which in turn depends on the important work of Stewart in [Reference Stewart17]. In particular, they showed that the number of cube-free integers d with
![]() $|d| \leq X$
such that the equation
$|d| \leq X$
such that the equation
defines an elliptic curve with rank at least
![]() $2$
is asymptotically greater than
$2$
is asymptotically greater than
![]() $X^{1/3}$
. We, of course, do not need such a strong statement; indeed, we only need one such d. This completes the proof for the case
$X^{1/3}$
. We, of course, do not need such a strong statement; indeed, we only need one such d. This completes the proof for the case
![]() $m_1 \geq 3$
.
$m_1 \geq 3$
.
We proceed to handle the case
![]() $m_1 = 2, m_2 \geq 4$
. Using the same notation as in (5.2), we then set
$m_1 = 2, m_2 \geq 4$
. Using the same notation as in (5.2), we then set
and set
This gives a curve
We need to choose square-free d so that this curve has infinitely many integral solutions, and such a d exists by Theorem 2.2. The height
![]() $H_{({\mathbf {a}}, Bm)}(x,y)$
is given by
$H_{({\mathbf {a}}, Bm)}(x,y)$
is given by
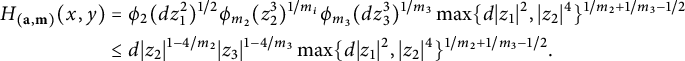 $$ \begin{align*} H_{({\mathbf{a}}, {\mathbf{m}})}(x,y) & = \phi_2(dz_1^2)^{1/2} \phi_{m_2}(z_2^3)^{1/m_i} \phi_{m_3}(d z_3^3)^{1/m_3} \max\{d|z_1|^2, |z_2|^4\}^{1/m_2 + 1/m_3 - 1/2} \\ & \leq d |z_2|^{1 - 4/m_2} |z_3|^{1 - 4/m_3} \max\{d|z_1|^2, |z_2|^4\}^{1/m_2 + 1/m_3 - 1/2}. \end{align*} $$
$$ \begin{align*} H_{({\mathbf{a}}, {\mathbf{m}})}(x,y) & = \phi_2(dz_1^2)^{1/2} \phi_{m_2}(z_2^3)^{1/m_i} \phi_{m_3}(d z_3^3)^{1/m_3} \max\{d|z_1|^2, |z_2|^4\}^{1/m_2 + 1/m_3 - 1/2} \\ & \leq d |z_2|^{1 - 4/m_2} |z_3|^{1 - 4/m_3} \max\{d|z_1|^2, |z_2|^4\}^{1/m_2 + 1/m_3 - 1/2}. \end{align*} $$
Note that
so we obtain the upper bound
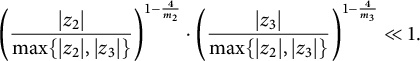 $$\begin{align*}\left(\frac{|z_2|}{\max\{|z_2|, |z_3|\}}\right)^{1 - \frac{4}{m_2}} \cdot \left(\frac{|z_3|}{\max\{|z_2|, |z_3|\}} \right)^{1 - \frac{4}{m_3}} \ll 1. \end{align*}$$
$$\begin{align*}\left(\frac{|z_2|}{\max\{|z_2|, |z_3|\}}\right)^{1 - \frac{4}{m_2}} \cdot \left(\frac{|z_3|}{\max\{|z_2|, |z_3|\}} \right)^{1 - \frac{4}{m_3}} \ll 1. \end{align*}$$
It follows that there are infinitely many integers
![]() $x,y$
such that
$x,y$
such that
![]() $H_{({\mathbf {a}}, {\mathbf {m}})}(x,y)$
remains bounded.
$H_{({\mathbf {a}}, {\mathbf {m}})}(x,y)$
remains bounded.
Finally, we resolve the case
![]() $m_1 = 2, m_2 = 3, m_3 \geq 6$
. In this case, we use the fact that there exist integers
$m_1 = 2, m_2 = 3, m_3 \geq 6$
. In this case, we use the fact that there exist integers
![]() $a,b,c$
with a square-free, b cube-free, and c sixth power-free such that the equation
$a,b,c$
with a square-free, b cube-free, and c sixth power-free such that the equation
has infinitely many primitive solutions (see [Reference Darmon and Granville5, Section 6.3]). Thus, by fixing such a triple
![]() $(a,b,c)$
and setting
$(a,b,c)$
and setting
and
we specialized a point on
![]() $\mathfrak {X}({\mathbb {P}}^1 : (0, 2), (\infty , 3), (-1, 6))$
to the curve given by (5.3). The height of such a point is then bounded in terms of
$\mathfrak {X}({\mathbb {P}}^1 : (0, 2), (\infty , 3), (-1, 6))$
to the curve given by (5.3). The height of such a point is then bounded in terms of
![]() $a,b,c$
only, and is thus absolutely bounded. This shows that the Northcott property fails in this case as well.
$a,b,c$
only, and is thus absolutely bounded. This shows that the Northcott property fails in this case as well.
This concludes the proof of Theorem 2.1.
5.3 Proof of Theorems 2.5
We proceed to prove Theorem 2.5. The claim when
![]() $\delta ({\mathbf {m}}) = 0$
is covered in Theorem 2.1, so we will not discuss it again. When
$\delta ({\mathbf {m}}) = 0$
is covered in Theorem 2.1, so we will not discuss it again. When
![]() $\delta ({\mathbf {m}})> 0$
, we note that
$\delta ({\mathbf {m}})> 0$
, we note that
![]() $n = 3$
, and that in each such case, there exist integers
$n = 3$
, and that in each such case, there exist integers
![]() $a_{\mathbf {m}}, b_{\mathbf {m}}, c_{\mathbf {m}}$
such that the equation
$a_{\mathbf {m}}, b_{\mathbf {m}}, c_{\mathbf {m}}$
such that the equation
has infinitely many primitive integral solutions (see, for example, [Reference Beukers1]). This shows that the Northcott property fails for
![]() $H^0$
.
$H^0$
.
We may now work with the case when
![]() $\delta ({\mathbf {m}}) < 0$
. We see that the height
$\delta ({\mathbf {m}}) < 0$
. We see that the height
![]() $H^0$
is bounded below by
$H^0$
is bounded below by
so it suffices to show that this quantity necessarily goes to infinity. We then use the notation from (5.2), to obtain the equation
 $$ \begin{align} x_{1,m_1}^{m_1} \prod_{j=1}^{m_1 - 1} x_{1,j}^j + x_{2,m_2}^{m_2} \prod_{j=1}^{m_2 - 1} x_{2,j}^{j} = x_{3,m_3}^{m_3} \prod_{j=1}^{m_3 - 1} x_{3,j}^j. \end{align} $$
$$ \begin{align} x_{1,m_1}^{m_1} \prod_{j=1}^{m_1 - 1} x_{1,j}^j + x_{2,m_2}^{m_2} \prod_{j=1}^{m_2 - 1} x_{2,j}^{j} = x_{3,m_3}^{m_3} \prod_{j=1}^{m_3 - 1} x_{3,j}^j. \end{align} $$
By convention, we have that
![]() $x_{i,j}$
is square-free for
$x_{i,j}$
is square-free for
![]() $1 \leq i \leq 3$
and
$1 \leq i \leq 3$
and
![]() $1 \leq j \leq m_i - 1$
. Thus, (5.4) is equal to
$1 \leq j \leq m_i - 1$
. Thus, (5.4) is equal to
 $$\begin{align*}\prod_{j=1}^{m_1 - 1} x_{1,j}^{\frac{m_1 - j}{m_1}} \prod_{j=1}^{m_2 - 1} x_{2,j}^{\frac{m_2 - j}{m_2}} \prod_{j=1}^{m_3 - 1} x_{3,j}^{\frac{m_3 - j}{m_3}}.\end{align*}$$
$$\begin{align*}\prod_{j=1}^{m_1 - 1} x_{1,j}^{\frac{m_1 - j}{m_1}} \prod_{j=1}^{m_2 - 1} x_{2,j}^{\frac{m_2 - j}{m_2}} \prod_{j=1}^{m_3 - 1} x_{3,j}^{\frac{m_3 - j}{m_3}}.\end{align*}$$
Viewing these products as coefficients in (5.5), we see that if
![]() $H^0$
is to be bounded, these coefficients must be bounded. Therefore, it suffices to check that for a fixed triple of integers
$H^0$
is to be bounded, these coefficients must be bounded. Therefore, it suffices to check that for a fixed triple of integers
![]() $a,b,c$
, the equation
$a,b,c$
, the equation
has finitely many primitive integer solutions when
![]() $1/m_1 + 1/m_2 + 1/m_3 < 1$
. But this is exactly the content of Darmon and Granville’s paper [Reference Darmon and Granville5], so we are done.
$1/m_1 + 1/m_2 + 1/m_3 < 1$
. But this is exactly the content of Darmon and Granville’s paper [Reference Darmon and Granville5], so we are done.
6 Northcott property of perturbed anti-canonical heights and the
 $abc$
-conjecture
$abc$
-conjecture
In this section, we prove Theorem 1.3, starting with Theorem 2.6. We consider the property of recovering Northcott’s property on a modified ESZ-B anti-canonical height on the stacky curve
Here, the modified height takes the shape
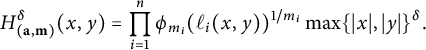 $$\begin{align*}H_{({\mathbf{a}}, {\mathbf{m}})}^\delta (x,y) = \prod_{i=1}^n \phi_{m_i} (\ell_i(x,y))^{1/m_i} \max\{|x|, |y|\}^{\delta}.\end{align*}$$
$$\begin{align*}H_{({\mathbf{a}}, {\mathbf{m}})}^\delta (x,y) = \prod_{i=1}^n \phi_{m_i} (\ell_i(x,y))^{1/m_i} \max\{|x|, |y|\}^{\delta}.\end{align*}$$
Since
![]() $\chi (\mathfrak {X})=\delta ({\mathbf {m}})=2-\sum _{i=1}^n(1-\frac {1}{m_i})\leq 0$
, our goal is to show that
$\chi (\mathfrak {X})=\delta ({\mathbf {m}})=2-\sum _{i=1}^n(1-\frac {1}{m_i})\leq 0$
, our goal is to show that
assuming the
![]() $abc$
-conjecture. Recall that we have shown that
$abc$
-conjecture. Recall that we have shown that
![]() $ H^{\chi (\mathfrak {X})}_{({\mathbf {a}},{\mathbf {m}})}$
does not have the Northcott property unconditionally. Thus, we must show that
$ H^{\chi (\mathfrak {X})}_{({\mathbf {a}},{\mathbf {m}})}$
does not have the Northcott property unconditionally. Thus, we must show that
![]() $ H^{\chi (\mathfrak {X})+\kappa }_{({\mathbf {a}},{\mathbf {m}})}$
has the Northcott property for all
$ H^{\chi (\mathfrak {X})+\kappa }_{({\mathbf {a}},{\mathbf {m}})}$
has the Northcott property for all
![]() $\kappa>0$
. First, assume that
$\kappa>0$
. First, assume that
![]() $\chi (\mathfrak {X})=0$
. The Northcott property for the standard height implies that
$\chi (\mathfrak {X})=0$
. The Northcott property for the standard height implies that
![]() $H_{({\mathbf {a}}, {\mathbf {m}})}^\delta (x,y)$
has the Northcott property whenever
$H_{({\mathbf {a}}, {\mathbf {m}})}^\delta (x,y)$
has the Northcott property whenever
![]() $\delta>0$
. So
$\delta>0$
. So
![]() $\inf \{\delta \in {\mathbb {R}}\colon H^\delta _{({\mathbf {a}},{\mathbf {m}})}\ \mathrm{has\ the\ Northcott\ property}\}=0=\chi (\mathfrak {X})$
as needed. Now suppose that
$\inf \{\delta \in {\mathbb {R}}\colon H^\delta _{({\mathbf {a}},{\mathbf {m}})}\ \mathrm{has\ the\ Northcott\ property}\}=0=\chi (\mathfrak {X})$
as needed. Now suppose that
![]() $\chi (\mathfrak {X})<0$
. Assume, without loss of generality, that
$\chi (\mathfrak {X})<0$
. Assume, without loss of generality, that
![]() $m_1 \leq m_2 \leq \cdots \leq m_n$
. We then write
$m_1 \leq m_2 \leq \cdots \leq m_n$
. We then write
We have
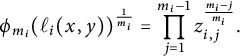 $$\begin{align*}\phi_{m_i}(\ell_i(x,y))^{\frac{1}{m_i}}=\prod_{j=1}^{m_i-1}z_{i,j}^{\frac{m_i-j}{m_i}}.\end{align*}$$
$$\begin{align*}\phi_{m_i}(\ell_i(x,y))^{\frac{1}{m_i}}=\prod_{j=1}^{m_i-1}z_{i,j}^{\frac{m_i-j}{m_i}}.\end{align*}$$
It follows that
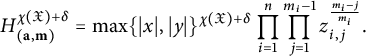 $$\begin{align*}H^{\chi(\mathfrak{X})+\delta}_{({\mathbf{a}},{\mathbf{m}})}=\max\{\vert x\vert,\vert y\vert\}^{\chi(\mathfrak{X})+\delta}\prod_{i=1}^n\prod_{j=1}^{m_i-1}z_{i,j}^{\frac{m_i-j}{m_i}}.\end{align*}$$
$$\begin{align*}H^{\chi(\mathfrak{X})+\delta}_{({\mathbf{a}},{\mathbf{m}})}=\max\{\vert x\vert,\vert y\vert\}^{\chi(\mathfrak{X})+\delta}\prod_{i=1}^n\prod_{j=1}^{m_i-1}z_{i,j}^{\frac{m_i-j}{m_i}}.\end{align*}$$
Suppose that the following inequality holds for any
![]() $\epsilon>0$
:
$\epsilon>0$
:
 $$ \begin{align} \prod_{i=1}^n\prod_{j=1}^{m_i-1}z_{i,j}^{\frac{m_i-j}{m_i}}\gg_{\varepsilon} \max\{\vert x\vert,\vert y\vert\}^{-\chi(\mathfrak{X})-\varepsilon }. \end{align} $$
$$ \begin{align} \prod_{i=1}^n\prod_{j=1}^{m_i-1}z_{i,j}^{\frac{m_i-j}{m_i}}\gg_{\varepsilon} \max\{\vert x\vert,\vert y\vert\}^{-\chi(\mathfrak{X})-\varepsilon }. \end{align} $$
Then, by multiplying both sides of the equation by
![]() $ \max \{\vert x\vert ,\vert y\vert \}^{\chi (\mathfrak {X})+\kappa }$
, we obtain
$ \max \{\vert x\vert ,\vert y\vert \}^{\chi (\mathfrak {X})+\kappa }$
, we obtain
 $$ \begin{align} \max\{\vert x\vert,\vert y\vert\}^{\chi(\mathfrak{X})+\kappa}\prod_{i=1}^n\prod_{j=1}^{m_i-1}z_{i,j}^{\frac{m_i-j}{m_i}}\gg_{\varepsilon} \max\{\vert x\vert,\vert y\vert\}^{\kappa-\epsilon }. \end{align} $$
$$ \begin{align} \max\{\vert x\vert,\vert y\vert\}^{\chi(\mathfrak{X})+\kappa}\prod_{i=1}^n\prod_{j=1}^{m_i-1}z_{i,j}^{\frac{m_i-j}{m_i}}\gg_{\varepsilon} \max\{\vert x\vert,\vert y\vert\}^{\kappa-\epsilon }. \end{align} $$
Taking
![]() $\varepsilon =\frac {\kappa }{2}$
, we have that
$\varepsilon =\frac {\kappa }{2}$
, we have that
Thus,
![]() $H_{({\mathbf {a}}, {\mathbf {m}})}^{\chi (\mathfrak {X})+\kappa } (x,y)$
must have the Northcott property as it cannot remain bounded by the usual Northcott property for
$H_{({\mathbf {a}}, {\mathbf {m}})}^{\chi (\mathfrak {X})+\kappa } (x,y)$
must have the Northcott property as it cannot remain bounded by the usual Northcott property for
![]() ${\mathbb {P}}^1$
. Therefore, we are done if we can confirm inequality (6.1). To do so, we require the following proposition, due to Granville [Reference Granville11].
${\mathbb {P}}^1$
. Therefore, we are done if we can confirm inequality (6.1). To do so, we require the following proposition, due to Granville [Reference Granville11].
Proposition 6.1 (Granville)
Suppose that the
![]() $abc$
-conjecture holds. Then, for any binary form F with nonzero discriminant and
$abc$
-conjecture holds. Then, for any binary form F with nonzero discriminant and
![]() $\varepsilon> 0$
, we have
$\varepsilon> 0$
, we have
In other words, if the
![]() $abc$
-conjecture holds, then the radical of
$abc$
-conjecture holds, then the radical of
![]() $F(m,n)$
will be quite large compared to the variables
$F(m,n)$
will be quite large compared to the variables
![]() $m,n$
(provided that the degree is at least 3).
$m,n$
(provided that the degree is at least 3).
We will apply Proposition 6.1 to reduce the proof of Theorem 2.6 to a linear programming problem.
6.1 A linear program bound
Observe that for each
![]() $1 \leq i \leq n$
,
$1 \leq i \leq n$
,
 $$\begin{align*}\prod_{j=1}^{m_i} z_{i, j} \geq \text{rad}\left( \prod_{j=1}^{m_i} z_{i,j} \right).\end{align*}$$
$$\begin{align*}\prod_{j=1}^{m_i} z_{i, j} \geq \text{rad}\left( \prod_{j=1}^{m_i} z_{i,j} \right).\end{align*}$$
Applying Proposition 6.1 to the binary form
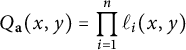 $$\begin{align*}Q_{\mathbf{a}}(x,y) = \prod_{i=1}^n \ell_i(x,y) \end{align*}$$
$$\begin{align*}Q_{\mathbf{a}}(x,y) = \prod_{i=1}^n \ell_i(x,y) \end{align*}$$
in conjunction with the above observation, we obtain
 $$ \begin{align} \prod_{i=1}^n \prod_{j=1}^{m_i} z_{i,j} \geq \operatorname{rad} \left(\prod_{i=1}^n \ell_i(x,y) \right) \gg_{\varepsilon} \max\{|x|, |y|\}^{n - 2 - \varepsilon}. \end{align} $$
$$ \begin{align} \prod_{i=1}^n \prod_{j=1}^{m_i} z_{i,j} \geq \operatorname{rad} \left(\prod_{i=1}^n \ell_i(x,y) \right) \gg_{\varepsilon} \max\{|x|, |y|\}^{n - 2 - \varepsilon}. \end{align} $$
Similarly, for each i, we have the bound
Taking logarithms and writing
![]() $y_{i,j} = \log |z_{i,j}|$
, we then have an optimization problem:
$y_{i,j} = \log |z_{i,j}|$
, we then have an optimization problem:
 $$ \begin{align} \min \sum_{i=1}^n \frac{1}{m_i} \sum_{j=1}^{m_i - 1} (m_i -j) y_{i,j} \end{align} $$
$$ \begin{align} \min \sum_{i=1}^n \frac{1}{m_i} \sum_{j=1}^{m_i - 1} (m_i -j) y_{i,j} \end{align} $$
subject to
 $$ \begin{align} \sum_{i=1}^n \sum_{j=1}^{m_i} y_{i,j} \geq (n-2 -\varepsilon) \log B \end{align} $$
$$ \begin{align} \sum_{i=1}^n \sum_{j=1}^{m_i} y_{i,j} \geq (n-2 -\varepsilon) \log B \end{align} $$
and
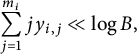 $$ \begin{align} \sum_{j=1}^{m_i} j y_{i,j} \ll \log B, \end{align} $$
$$ \begin{align} \sum_{j=1}^{m_i} j y_{i,j} \ll \log B, \end{align} $$
where
![]() $B = \max \{|x|, |y|\}$
. Further, we have
$B = \max \{|x|, |y|\}$
. Further, we have
![]() $y_{i,j} \geq 0$
for all
$y_{i,j} \geq 0$
for all
![]() $i,j$
.
$i,j$
.
We emphasize that, at this point, integrality no longer plays a role, and neither does the syzygies relating the
![]() $z_{i,j}$
’s. Indeed, we only need to solve the above linear program allowing arbitrary real inputs.
$z_{i,j}$
’s. Indeed, we only need to solve the above linear program allowing arbitrary real inputs.
Now put
for
![]() $1\leq i\leq n$
and
$1\leq i\leq n$
and
![]() $1\leq j\leq m_i-1$
. Write
$1\leq j\leq m_i-1$
. Write
![]() $c_{i,m_i}=0$
and let
$c_{i,m_i}=0$
and let
![]() ${\mathbf {c}}=(c_{i,j})$
to be the column vector with
${\mathbf {c}}=(c_{i,j})$
to be the column vector with
We have that
![]() ${\mathbf {c}}\in {\mathbb {R}}^{N}$
where
${\mathbf {c}}\in {\mathbb {R}}^{N}$
where
![]() $N=\sum _{i=1}^n n m_i$
.
$N=\sum _{i=1}^n n m_i$
.
Let A be the matrix with rows representing the constraints,
 $$ \begin{align} C_0&:\sum_{i=1}^n \sum_{j=1}^{m_i} y_{i,j} \geq (n-2 -\varepsilon) \log B \end{align} $$
$$ \begin{align} C_0&:\sum_{i=1}^n \sum_{j=1}^{m_i} y_{i,j} \geq (n-2 -\varepsilon) \log B \end{align} $$
 $$ \begin{align} C_i&:-\sum_{j=1}^{m_i} j y_{i,j} \gg -\log B.\qquad\quad \end{align} $$
$$ \begin{align} C_i&:-\sum_{j=1}^{m_i} j y_{i,j} \gg -\log B.\qquad\quad \end{align} $$
If we have taken
![]() ${\mathbf {e}}_{i,j}$
to be a basis of
${\mathbf {e}}_{i,j}$
to be a basis of
![]() ${\mathbb {R}}^N$
, then we have that the rows of A are given by
${\mathbb {R}}^N$
, then we have that the rows of A are given by
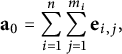 $$ \begin{align} {\mathbf{a}}_0&=\sum_{i=1}^n\sum_{j=1}^{m_i}{\mathbf{e}}_{i,j}, \end{align} $$
$$ \begin{align} {\mathbf{a}}_0&=\sum_{i=1}^n\sum_{j=1}^{m_i}{\mathbf{e}}_{i,j}, \end{align} $$
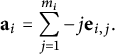 $$ \begin{align} {\mathbf{a}}_i&=\sum_{j=1}^{m_i}-j{\mathbf{e}}_{i,j}. \end{align} $$
$$ \begin{align} {\mathbf{a}}_i&=\sum_{j=1}^{m_i}-j{\mathbf{e}}_{i,j}. \end{align} $$
Finally, let
![]() ${\mathbf {b}}$
be the column vector with
${\mathbf {b}}$
be the column vector with
![]() $n+1$
entries representing the constraints given by (6.7) and (6.8). In other words, we have
$n+1$
entries representing the constraints given by (6.7) and (6.8). In other words, we have
Our linear programming problem is then the following: Let
![]() ${\mathbf {y}}=(y_{ij})$
ordered as above.
${\mathbf {y}}=(y_{ij})$
ordered as above.
 $$ \begin{align} &\mathrm{Minimize}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\mathbf{c}}^{T}{\mathbf{y}},\\ &\mathrm{subject\ to}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A{\mathbf{y}}\geq {\mathbf{b}}\ \mathrm{and}\ {\mathbf{y}}\geq 0. \notag \end{align} $$
$$ \begin{align} &\mathrm{Minimize}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\mathbf{c}}^{T}{\mathbf{y}},\\ &\mathrm{subject\ to}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A{\mathbf{y}}\geq {\mathbf{b}}\ \mathrm{and}\ {\mathbf{y}}\geq 0. \notag \end{align} $$
The dual linear program is
 $$ \begin{align} &\mathrm{Maximize}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\mathbf{b}}^{T}{\mathbf{x}},\\ &\mathrm{subject\ to}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A^T{\mathbf{x}}\leq {\mathbf{c}}\ \mathrm{and}\ {\mathbf{x}}\geq 0, \notag \end{align} $$
$$ \begin{align} &\mathrm{Maximize}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\mathbf{b}}^{T}{\mathbf{x}},\\ &\mathrm{subject\ to}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A^T{\mathbf{x}}\leq {\mathbf{c}}\ \mathrm{and}\ {\mathbf{x}}\geq 0, \notag \end{align} $$
where
![]() ${\mathbf {x}}=[x_0,x_1,...,x_n]$
. We call a vector
${\mathbf {x}}=[x_0,x_1,...,x_n]$
. We call a vector
![]() ${\mathbf {x}}$
dual feasible if
${\mathbf {x}}$
dual feasible if
![]() $A^T{\mathbf {x}}\leq {\mathbf {c}}$
and vector
$A^T{\mathbf {x}}\leq {\mathbf {c}}$
and vector
![]() ${\mathbf {y}}$
primal feasible if
${\mathbf {y}}$
primal feasible if
![]() $A{\mathbf {y}}\geq {\mathbf {b}}$
. We have the following well-known weak duality statement.
$A{\mathbf {y}}\geq {\mathbf {b}}$
. We have the following well-known weak duality statement.
Lemma 6.2 (Weak duality)
Let A be an
![]() $m\times n$
matrix with real entries and
$m\times n$
matrix with real entries and
![]() ${\mathbf {c}}$
an
${\mathbf {c}}$
an
![]() $n\times 1$
real vector and
$n\times 1$
real vector and
![]() ${\mathbf {b}}$
an
${\mathbf {b}}$
an
![]() $m\times 1$
real vector. Consider the primal linear program
$m\times 1$
real vector. Consider the primal linear program
 $$ \begin{align*} &\mathrm{Minimize}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\mathbf{c}}^{T},\\ &\mathrm{subject\ to}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A{\mathbf{y}}\geq {\mathbf{b}}\ \mathrm{and}\ {\mathbf{y}}\geq 0 \end{align*} $$
$$ \begin{align*} &\mathrm{Minimize}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\mathbf{c}}^{T},\\ &\mathrm{subject\ to}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A{\mathbf{y}}\geq {\mathbf{b}}\ \mathrm{and}\ {\mathbf{y}}\geq 0 \end{align*} $$
and the dual linear program
 $$ \begin{align*} &\mathrm{Maximize}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\mathbf{b}}^{T}{\mathbf{x}},\\ &\mathrm{subject\ to}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A^T{\mathbf{x}}\leq {\mathbf{c}}\ \mathrm{and}\ {\mathbf{x}}\geq 0. \end{align*} $$
$$ \begin{align*} &\mathrm{Maximize}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\mathbf{b}}^{T}{\mathbf{x}},\\ &\mathrm{subject\ to}{:}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A^T{\mathbf{x}}\leq {\mathbf{c}}\ \mathrm{and}\ {\mathbf{x}}\geq 0. \end{align*} $$
Let
![]() ${\mathbf {y}}$
be any primal feasible vector and
${\mathbf {y}}$
be any primal feasible vector and
![]() ${\mathbf {x}}$
a dual feasible vector. Then
${\mathbf {x}}$
a dual feasible vector. Then
Proof Let
![]() $A=(a_{i,j})$
. Because
$A=(a_{i,j})$
. Because
![]() ${\mathbf {y}}$
is primal feasible, we have
${\mathbf {y}}$
is primal feasible, we have
![]() $A{\mathbf {y}}\geq {\mathbf {b}}$
. Therefore, for all
$A{\mathbf {y}}\geq {\mathbf {b}}$
. Therefore, for all
![]() $1\leq i\leq m$
, we have
$1\leq i\leq m$
, we have
 $$\begin{align*}\sum_{j=1}^na_{i,j}y_j\geq b_i. \end{align*}$$
$$\begin{align*}\sum_{j=1}^na_{i,j}y_j\geq b_i. \end{align*}$$
Multiplying by
![]() $x_i$
and summing over all i, we have
$x_i$
and summing over all i, we have
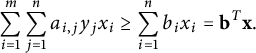 $$ \begin{align} \sum_{i=1}^m\sum_{j=1}^na_{i,j}y_jx_i\geq \sum_{i=1}^n b_ix_i={\mathbf{b}}^{T}{\mathbf{x}}. \end{align} $$
$$ \begin{align} \sum_{i=1}^m\sum_{j=1}^na_{i,j}y_jx_i\geq \sum_{i=1}^n b_ix_i={\mathbf{b}}^{T}{\mathbf{x}}. \end{align} $$
On the other hand, because
![]() ${\mathbf {x}}$
is dual feasible, we have that
${\mathbf {x}}$
is dual feasible, we have that
![]() $A^T{\mathbf {x}}\leq {\mathbf {c}}$
, so for each
$A^T{\mathbf {x}}\leq {\mathbf {c}}$
, so for each
![]() $1\leq j\leq n$
, we have
$1\leq j\leq n$
, we have
 $$\begin{align*}\sum_{i=1}^ma_{j,i}x_i\leq c_j.\end{align*}$$
$$\begin{align*}\sum_{i=1}^ma_{j,i}x_i\leq c_j.\end{align*}$$
Multiplying by
![]() $y_j$
and summing over all j gives
$y_j$
and summing over all j gives
 $$ \begin{align} \sum_{j=1}^n\sum_{i=1}^ma_{i,j}x_iy_j\leq \sum_{j=1}^ny_jc_j={\mathbf{c}}^{T}{\mathbf{y}}. \end{align} $$
$$ \begin{align} \sum_{j=1}^n\sum_{i=1}^ma_{i,j}x_iy_j\leq \sum_{j=1}^ny_jc_j={\mathbf{c}}^{T}{\mathbf{y}}. \end{align} $$
Combining inequality (6.17) and inequality (6.18) gives
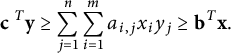 $$\begin{align*}{\mathbf{c}}^{\ T}{\mathbf{y}}\geq \sum_{j=1}^n\sum_{i=1}^ma_{i,j}x_iy_j\geq {\mathbf{b}}^{T}{\mathbf{x}}.\\[-41pt] \end{align*}$$
$$\begin{align*}{\mathbf{c}}^{\ T}{\mathbf{y}}\geq \sum_{j=1}^n\sum_{i=1}^ma_{i,j}x_iy_j\geq {\mathbf{b}}^{T}{\mathbf{x}}.\\[-41pt] \end{align*}$$
Returning to our problem, the weak duality theorem tells us that it suffices to find a dual feasible solution
![]() ${\mathbf {x}}=[x_0,\dots x_n]$
such that
${\mathbf {x}}=[x_0,\dots x_n]$
such that
![]() ${\mathbf {b}}^{T}{\mathbf {x}}\geq -\chi (\mathfrak {X})+\epsilon $
. In other words, we seek
${\mathbf {b}}^{T}{\mathbf {x}}\geq -\chi (\mathfrak {X})+\epsilon $
. In other words, we seek
![]() ${\mathbf {x}}=[x_0,\dots , x_n]$
with
${\mathbf {x}}=[x_0,\dots , x_n]$
with
 $$ \begin{align*} {\mathbf{b}}^{T}{\mathbf{x}}&=\log B\left((n-2-\epsilon)x_1-\sum_{j=1}^nx_i\right)\geq -\chi(\mathfrak{X})+\epsilon, \\ A^T{\mathbf{x}}&\leq {\mathbf{c}},\\ {\mathbf{x}}&\geq 0. \end{align*} $$
$$ \begin{align*} {\mathbf{b}}^{T}{\mathbf{x}}&=\log B\left((n-2-\epsilon)x_1-\sum_{j=1}^nx_i\right)\geq -\chi(\mathfrak{X})+\epsilon, \\ A^T{\mathbf{x}}&\leq {\mathbf{c}},\\ {\mathbf{x}}&\geq 0. \end{align*} $$
Take
![]() ${\mathbf {x}}=[1,\frac {1}{m_1},\frac {1}{m_2},\dots ,\frac {1}{m_n}]$
. We first show that
${\mathbf {x}}=[1,\frac {1}{m_1},\frac {1}{m_2},\dots ,\frac {1}{m_n}]$
. We first show that
![]() ${\mathbf {x}}$
is dual feasible. In this case, A is an
${\mathbf {x}}$
is dual feasible. In this case, A is an
![]() $(n+1)\times \sum _{i=1}^n m_i$
matrix. So a row of
$(n+1)\times \sum _{i=1}^n m_i$
matrix. So a row of
![]() $A^T$
is indexed by a pair
$A^T$
is indexed by a pair
![]() $(i,j)$
with
$(i,j)$
with
![]() $1\leq i\leq n$
and
$1\leq i\leq n$
and
![]() $1\leq j\leq m_i$
. We have that the
$1\leq j\leq m_i$
. We have that the
![]() $(i,j)$
entry of
$(i,j)$
entry of
![]() $A^T{\mathbf {x}}={\mathbf {x}}^{T}A$
can be computed as
$A^T{\mathbf {x}}={\mathbf {x}}^{T}A$
can be computed as
Therefore, to show that
![]() ${\mathbf {x}}$
is dual feasible for an arbitrary
${\mathbf {x}}$
is dual feasible for an arbitrary
![]() ${\mathbb {X}}$
, we need that
${\mathbb {X}}$
, we need that
In our case, the
![]() $(i,j)$
entry of
$(i,j)$
entry of
![]() $A^T{\mathbf {x}}$
is given by
$A^T{\mathbf {x}}$
is given by
so
![]() ${\mathbf {x}}$
is dual feasible. We then compute
${\mathbf {x}}$
is dual feasible. We then compute
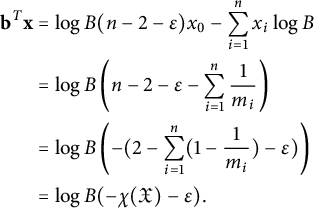 $$ \begin{align*} {\mathbf{b}}^{T}{\mathbf{x}}&=\log B(n-2-\varepsilon)x_0-\sum_{i=1}^nx_i\log B\\ &=\log B\left(n-2-\varepsilon-\sum_{i=1}^n\dfrac{1}{m_i}\right)\\ &=\log B\left( -(2-\sum_{i=1}^n(1-\dfrac{1}{m_i})-\epsilon )\right)\\ &=\log B(-\chi(\mathfrak{X})-\epsilon). \end{align*} $$
$$ \begin{align*} {\mathbf{b}}^{T}{\mathbf{x}}&=\log B(n-2-\varepsilon)x_0-\sum_{i=1}^nx_i\log B\\ &=\log B\left(n-2-\varepsilon-\sum_{i=1}^n\dfrac{1}{m_i}\right)\\ &=\log B\left( -(2-\sum_{i=1}^n(1-\dfrac{1}{m_i})-\epsilon )\right)\\ &=\log B(-\chi(\mathfrak{X})-\epsilon). \end{align*} $$
Therefore,
![]() ${\mathbf {x}}=\left (1,\dfrac {1}{m_1},\dots ,\dfrac {1}{m_n} \right )$
is a dual feasible solution and
${\mathbf {x}}=\left (1,\dfrac {1}{m_1},\dots ,\dfrac {1}{m_n} \right )$
is a dual feasible solution and
By the weak duality theorem, we have that
 $$\begin{align*}\sum_{i=1}^n \frac{1}{m_i} \sum_{j=1}^{m_i - 1} (m_i -j) y_{i,j}\geq \log B(-\chi(\mathfrak{X})-\epsilon). \end{align*}$$
$$\begin{align*}\sum_{i=1}^n \frac{1}{m_i} \sum_{j=1}^{m_i - 1} (m_i -j) y_{i,j}\geq \log B(-\chi(\mathfrak{X})-\epsilon). \end{align*}$$
Exponentiating gives
 $$\begin{align*}\prod_{i=1}^n\prod_{j=1}^{m_i-1}z_{i,j}^{\frac{m_i-j}{m_i}}\geq B^{(-\chi(\mathfrak{X})-\epsilon)}. \end{align*}$$
$$\begin{align*}\prod_{i=1}^n\prod_{j=1}^{m_i-1}z_{i,j}^{\frac{m_i-j}{m_i}}\geq B^{(-\chi(\mathfrak{X})-\epsilon)}. \end{align*}$$
As
![]() $B=\max \{\vert x\vert ,\vert y\vert \}$
, we have verified inequality (6.1) and consequently we have that conditional on the
$B=\max \{\vert x\vert ,\vert y\vert \}$
, we have verified inequality (6.1) and consequently we have that conditional on the
![]() $abc$
-conjecture that
$abc$
-conjecture that
when
![]() $\chi (\mathfrak {X})\leq 0$
.
$\chi (\mathfrak {X})\leq 0$
.
6.2 Proof of Theorem 1.3
One direction of the theorem is provided by Theorem 2.6, which we proved in the previous subsection. It suffices to prove the converse.
Actually, for the converse, we only need the assertion that for any
![]() $\kappa> 0$
and
$\kappa> 0$
and
![]() $m \geq 4$
, the function
$m \geq 4$
, the function
![]() $H_{-K_{\mathfrak {X}_m}}({\mathbf {x}}) \cdot H({\mathbf {x}})^\kappa $
has Northcott’s property, where
$H_{-K_{\mathfrak {X}_m}}({\mathbf {x}}) \cdot H({\mathbf {x}})^\kappa $
has Northcott’s property, where
![]() $\mathfrak {X}_m = \mathfrak {X}({\mathbb {P}}^1 : ((0, 1, \infty ), (m, m, m))$
. To see this, let us fix
$\mathfrak {X}_m = \mathfrak {X}({\mathbb {P}}^1 : ((0, 1, \infty ), (m, m, m))$
. To see this, let us fix
![]() $\varepsilon> 0$
. Choose
$\varepsilon> 0$
. Choose
![]() $0 < \kappa < \varepsilon /3$
and choose
$0 < \kappa < \varepsilon /3$
and choose
![]() $m \in {\mathbb {N}}$
sufficiently large so that
$m \in {\mathbb {N}}$
sufficiently large so that
By hypothesis, we have
Trivially, we see that
for all
![]() $u \in {\mathbb {Z}}$
. Hence, (6.19) implies
$u \in {\mathbb {Z}}$
. Hence, (6.19) implies
Since
![]() $x,y,x+y$
are pairwise co-prime, we have
$x,y,x+y$
are pairwise co-prime, we have
![]() $\operatorname {rad}(x)\operatorname {rad}(y)\operatorname {rad}(x+y) = \operatorname {rad}(xy(x+y))$
; hence,
$\operatorname {rad}(x)\operatorname {rad}(y)\operatorname {rad}(x+y) = \operatorname {rad}(xy(x+y))$
; hence,
Raising both sides to the
![]() $m/(m-1)$
power, we have
$m/(m-1)$
power, we have
by our hypotheses on
![]() $m, \kappa $
. It follows that
$m, \kappa $
. It follows that
which is plainly equivalent to the
![]() $abc$
-conjecture, provided we adjust the implied constant.
$abc$
-conjecture, provided we adjust the implied constant.
7 Quantitative arithmetic of stacky curves
7.1 Crude bound for
 $N_{\mathbf {m}}(T)$
, with
$N_{\mathbf {m}}(T)$
, with
 ${\mathbf {m}} = (2,2,m)$
${\mathbf {m}} = (2,2,m)$
Here, we deal with the case
![]() ${\mathbf {m}} = (2,2,m)$
. The Euler characteristic is equal to
${\mathbf {m}} = (2,2,m)$
. The Euler characteristic is equal to
The height
![]() $H(x,y)$
is given by
$H(x,y)$
is given by
where
![]() $x = x_1 x_2^2, y = y_1 y_2^2$
and
$x = x_1 x_2^2, y = y_1 y_2^2$
and
with
![]() $x_1, y_1, z_1, \ldots , z_{m-1}$
square-free. We normalize the height by raising it to the mth power, obtaining the bound
$x_1, y_1, z_1, \ldots , z_{m-1}$
square-free. We normalize the height by raising it to the mth power, obtaining the bound
From here, we see that
whence we conclude that
 $$\begin{align*}|z_m| \ll \frac{T^{1/m}}{|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}|}.\end{align*}$$
$$\begin{align*}|z_m| \ll \frac{T^{1/m}}{|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}|}.\end{align*}$$
This bound and
![]() $|z_m| \geq 1$
implies that
$|z_m| \geq 1$
implies that
From here, we obtain a crude upper bound for
![]() $N_{\mathbf {m}}(T)$
, which proves Theorem 2.7. Indeed, having chosen
$N_{\mathbf {m}}(T)$
, which proves Theorem 2.7. Indeed, having chosen
![]() $x_1, y_1, z_1, \ldots , z_{m-1}$
, there are then
$x_1, y_1, z_1, \ldots , z_{m-1}$
, there are then
![]() $O(T^{1/m}/(|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}|)$
possibilities for
$O(T^{1/m}/(|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}|)$
possibilities for
![]() $z_m$
. Having chosen
$z_m$
. Having chosen
![]() $z_m$
as well, there are then
$z_m$
as well, there are then
![]() $O_{\varepsilon } (T^\varepsilon )$
possibilities for
$O_{\varepsilon } (T^\varepsilon )$
possibilities for
![]() $x_2, y_2$
, since
$x_2, y_2$
, since
![]() $x_2, y_2$
are polynomially bounded, so they will be determined by the norm-equation (7.1) up to a log factor. Thus, there are
$x_2, y_2$
are polynomially bounded, so they will be determined by the norm-equation (7.1) up to a log factor. Thus, there are
 $$ \begin{align} \sum_{|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}| \leq T^{1/m}} O_{\varepsilon} \left(\frac{T^{1/m + \varepsilon}}{|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}|} \right) \end{align} $$
$$ \begin{align} \sum_{|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}| \leq T^{1/m}} O_{\varepsilon} \left(\frac{T^{1/m + \varepsilon}}{|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}|} \right) \end{align} $$
possible solutions to (7.1) satisfying the height bound (7.2). We evaluate this as
 $$ \begin{align*} & \sum_{|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}| \leq T^{1/m}} O_{\varepsilon} \left(\frac{T^{1/m + \varepsilon}}{|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}|} \right) \\ & \quad = \sum_{|x_1 y_1| \leq T^{2/m}} \frac{1}{|x_1 y_1|^{1/2}} \sum_{|z_1 \cdots z_{m-1}| \leq T^{1/m}/|x_1 y_1|^{1/2}} O_{\varepsilon} \left(\frac{T^{1/m + \varepsilon}}{|z_1 \cdots z_{m-1}|} \right) \\ & \quad \ll_{\varepsilon} \sum_{|x_1 y_1| \leq T^{2/m}} \frac{T^{1/m + \varepsilon}}{|x_1 y_1|^{1/2}} \ll_{\varepsilon} T^{2/m + \varepsilon}. \end{align*} $$
$$ \begin{align*} & \sum_{|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}| \leq T^{1/m}} O_{\varepsilon} \left(\frac{T^{1/m + \varepsilon}}{|x_1 y_1|^{1/2} |z_1 \cdots z_{m-1}|} \right) \\ & \quad = \sum_{|x_1 y_1| \leq T^{2/m}} \frac{1}{|x_1 y_1|^{1/2}} \sum_{|z_1 \cdots z_{m-1}| \leq T^{1/m}/|x_1 y_1|^{1/2}} O_{\varepsilon} \left(\frac{T^{1/m + \varepsilon}}{|z_1 \cdots z_{m-1}|} \right) \\ & \quad \ll_{\varepsilon} \sum_{|x_1 y_1| \leq T^{2/m}} \frac{T^{1/m + \varepsilon}}{|x_1 y_1|^{1/2}} \ll_{\varepsilon} T^{2/m + \varepsilon}. \end{align*} $$
To give a lower bound, we choose square-free integers
![]() $a,b,c$
so that the curve
$a,b,c$
so that the curve
has a primitive integral solution. Such a triple is guaranteed to exist (see [Reference Beukers1]). Then we can parametrize (some) of the solutions by a triple of integral binary forms
![]() $(F,G, h)$
where
$(F,G, h)$
where
![]() $\deg F = \deg G = m$
and
$\deg F = \deg G = m$
and
![]() $\deg h = 2$
. By
$\deg h = 2$
. By
The height is
so if we treat
![]() $a,b,c$
as constants, then
$a,b,c$
as constants, then
Therefore, we are looking for solutions to the Thue inequality
If we restrict
![]() $u,v$
so that
$u,v$
so that
then we see that the above height bound is satisfied. Thus,
![]() $N_m(T) \gg T^{1/m}$
.
$N_m(T) \gg T^{1/m}$
.
7.2 Proof of Theorem 2.8
In this section, we prove Theorem 2.8. To do so, we will show that
![]() $N_2(T) = O \left (T^{1/2} (\log T)^3 \right )$
and give a separate argument to show that
$N_2(T) = O \left (T^{1/2} (\log T)^3 \right )$
and give a separate argument to show that
![]() $N_2(T) \gg T^{1/2} (\log T)^3$
. The incompatibility of these two arguments represents the main obstacle as to why an asymptotic formula for
$N_2(T) \gg T^{1/2} (\log T)^3$
. The incompatibility of these two arguments represents the main obstacle as to why an asymptotic formula for
![]() $N_2(T)$
remains elusive.
$N_2(T)$
remains elusive.
We count rational points of bounded height on the curve
![]() $\mathfrak {X}({\mathbb {P}}^1_{\mathbb {Q}};(0,2), (-1,2),(\infty ,2))$
with the height on
$\mathfrak {X}({\mathbb {P}}^1_{\mathbb {Q}};(0,2), (-1,2),(\infty ,2))$
with the height on
![]() ${\mathbb {P}}^1$
given by (2.7). On writing
${\mathbb {P}}^1$
given by (2.7). On writing
(note that this differs from the notation used elsewhere in the paper), we then have
and the max on the right-hand side is dependent only on the relative size of
![]() $|a|,|b|$
. If we write
$|a|,|b|$
. If we write
then we further obtain the expression
We may assume without loss of generality that
![]() $|x_1 y_1^2| \geq |x_2 y_2|^2$
and
$|x_1 y_1^2| \geq |x_2 y_2|^2$
and
![]() $x_1> 0$
, so that
$x_1> 0$
, so that
We consider the problem of counting integral points on the variety defined by (7.4), subject to the constraint
To obtain the upper bound, we must dissect (7.5) into suitable ranges. When
![]() $|x_1 x_2 x_3| \leq T^{1/2}$
, we fix
$|x_1 x_2 x_3| \leq T^{1/2}$
, we fix
![]() $x_1, x_2, x_3$
and treat (7.4) as a diagonal ternary quadratic form, say
$x_1, x_2, x_3$
and treat (7.4) as a diagonal ternary quadratic form, say
![]() $Q_{\mathbf {x}}$
. It is then the case that
$Q_{\mathbf {x}}$
. It is then the case that
for
![]() $i = 1,2,3$
, and by Corollary 2 of [Reference Browning and Heath-Brown3], we then have the estimate
$i = 1,2,3$
, and by Corollary 2 of [Reference Browning and Heath-Brown3], we then have the estimate
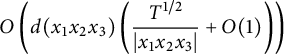 $$\begin{align*}O \left(d(x_1 x_2 x_3) \left(\frac{T^{1/2}}{|x_1 x_2 x_3|} + O(1) \right) \right) \end{align*}$$
$$\begin{align*}O \left(d(x_1 x_2 x_3) \left(\frac{T^{1/2}}{|x_1 x_2 x_3|} + O(1) \right) \right) \end{align*}$$
for the number of
![]() ${\mathbf {y}} \in {\mathbb {Z}}_{\ne 0}^3$
satisfying (7.5) and (7.4) provided that the quadratic form
${\mathbf {y}} \in {\mathbb {Z}}_{\ne 0}^3$
satisfying (7.5) and (7.4) provided that the quadratic form
![]() $Q_{\mathbf {x}}$
has a rational zero. Otherwise, it is clear that there will be no contribution. Thus, we must estimate
$Q_{\mathbf {x}}$
has a rational zero. Otherwise, it is clear that there will be no contribution. Thus, we must estimate
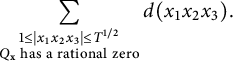 $$\begin{align*}\sum_{\substack{1 \leq |x_1 x_2 x_3| \leq T^{1/2} \\ Q_{\mathbf{x}} \text{ has a rational zero}}} d(x_1 x_2 x_3). \end{align*}$$
$$\begin{align*}\sum_{\substack{1 \leq |x_1 x_2 x_3| \leq T^{1/2} \\ Q_{\mathbf{x}} \text{ has a rational zero}}} d(x_1 x_2 x_3). \end{align*}$$
This is similar to the work of Guo in [Reference Guo12], except he counted with respect to the height
![]() $\lVert {\mathbf {x}} \rVert _\infty $
. Nevertheless, the techniques are similar, and again this may be of independent interest.
$\lVert {\mathbf {x}} \rVert _\infty $
. Nevertheless, the techniques are similar, and again this may be of independent interest.
Next, we must deal with the case when
![]() $|x_1 x_2 x_3| \geq T^{1/2}$
. For this, it suffices to observe from (7.6) that
$|x_1 x_2 x_3| \geq T^{1/2}$
. For this, it suffices to observe from (7.6) that
![]() $|x_1 x_2 x_3| \geq T^{1/2}$
implies
$|x_1 x_2 x_3| \geq T^{1/2}$
implies
 $$\begin{align*}|y_1 y_2 y_3| \leq \frac{T^{3/2}}{(x_1 x_2 x_3)^2} \leq T^{1/2}.\end{align*}$$
$$\begin{align*}|y_1 y_2 y_3| \leq \frac{T^{3/2}}{(x_1 x_2 x_3)^2} \leq T^{1/2}.\end{align*}$$
We then treat (7.4) as a linear form
![]() $L_{\mathbf {y}}$
in
$L_{\mathbf {y}}$
in
![]() ${\mathbf {x}}$
. We use this to show that the contribution for each
${\mathbf {x}}$
. We use this to show that the contribution for each
![]() ${\mathbf {y}}$
is
${\mathbf {y}}$
is
![]() $O\left (T^{1/2} |y_1 y_2 y_3|^{-1} + 1 \right )$
, which gives an acceptable contribution upon summing over
$O\left (T^{1/2} |y_1 y_2 y_3|^{-1} + 1 \right )$
, which gives an acceptable contribution upon summing over
![]() ${\mathbf {y}}$
.
${\mathbf {y}}$
.
For the lower bound, we first restrict
![]() $y_1, y_2, y_3 \in {\mathbb {Z}}_{\ne 0}$
satisfying
$y_1, y_2, y_3 \in {\mathbb {Z}}_{\ne 0}$
satisfying
for some explicit
![]() $\delta> 0$
to be specified later. We note that to obtain the correct order of magnitude, it is permissible to choose any
$\delta> 0$
to be specified later. We note that to obtain the correct order of magnitude, it is permissible to choose any
![]() $\delta> 0$
.
$\delta> 0$
.
Having fixed
![]() ${\mathbf {y}} = (y_1, y_2, y_3)$
, we consider the simultaneous conditions (7.4) and (7.5). This gives rise to a binary form inequality of the shape
${\mathbf {y}} = (y_1, y_2, y_3)$
, we consider the simultaneous conditions (7.4) and (7.5). This gives rise to a binary form inequality of the shape
Because
![]() $|y_1 y_2 y_3|$
is small, we can count the number of solutions
$|y_1 y_2 y_3|$
is small, we can count the number of solutions
![]() ${\mathbf {x}}$
to this inequality with reasonable precision. However, even with
${\mathbf {x}}$
to this inequality with reasonable precision. However, even with
![]() $|y_1 y_2 y_3|$
counting the number of solutions
$|y_1 y_2 y_3|$
counting the number of solutions
![]() ${\mathbf {x}}$
with enough uniformity appears to still be a challenging task, because the binary form in (7.7) is singular. This difficulty is exacerbated by the fact that we will need to apply a square-free sieve eventually to produce triples
${\mathbf {x}}$
with enough uniformity appears to still be a challenging task, because the binary form in (7.7) is singular. This difficulty is exacerbated by the fact that we will need to apply a square-free sieve eventually to produce triples
![]() ${\mathbf {x}}$
with each coordinate square-free.
${\mathbf {x}}$
with each coordinate square-free.
To get around this issue, we simply count solutions to (7.7) with
![]() $x_1, x_2$
satisfying the inequalities
$x_1, x_2$
satisfying the inequalities
for some positive numbers
![]() $c_1, c_2$
. This has the effect that the long cusps inherent in (7.7) are removed, and reduce the problem to a more straightforward geometry of numbers question.
$c_1, c_2$
. This has the effect that the long cusps inherent in (7.7) are removed, and reduce the problem to a more straightforward geometry of numbers question.
7.2.1 Upper bounds
To obtain upper bounds, it is crucial to view (7.4) as a plane in
![]() $x_1, x_2, x_3$
when
$x_1, x_2, x_3$
when
![]() $|y_1 y_2 y_3| \leq T^{1/2}$
and viewing (7.4) as a conic in
$|y_1 y_2 y_3| \leq T^{1/2}$
and viewing (7.4) as a conic in
![]() $y_1, y_2, y_3)$
when
$y_1, y_2, y_3)$
when
![]() $|x_1 x_2 x_3| \leq T^{1/2}$
. We call the former the linear case and the latter the quadratic case. We proceed to deal with the linear case below.
$|x_1 x_2 x_3| \leq T^{1/2}$
. We call the former the linear case and the latter the quadratic case. We proceed to deal with the linear case below.
We shall first suppose that
![]() $|y_1 y_2 y_3| \leq T^{1/2}$
is fixed, and count the triples
$|y_1 y_2 y_3| \leq T^{1/2}$
is fixed, and count the triples
![]() $(x_1, x_2, x_3)$
and
$(x_1, x_2, x_3)$
and
![]() $(y_1, y_2, y_3)$
for which (7.4) holds.
$(y_1, y_2, y_3)$
for which (7.4) holds.
The key is the following lemma on counting points in sublattices of
![]() ${\mathbb {Z}}^2$
.
${\mathbb {Z}}^2$
.
Lemma 7.1 Let
![]() $\Lambda \subset {\mathbb {Z}}^2$
be a lattice. Then, for all positive real numbers
$\Lambda \subset {\mathbb {Z}}^2$
be a lattice. Then, for all positive real numbers
![]() $R_1, R_2$
, the number of primitive integral points
$R_1, R_2$
, the number of primitive integral points
![]() ${\mathbf {x}} \in \Lambda $
satisfying
${\mathbf {x}} \in \Lambda $
satisfying
![]() $|x_i| \leq R_i, i = 1,2$
is at most
$|x_i| \leq R_i, i = 1,2$
is at most
![]() $O \left (R_1 R_2/\det (\Lambda ) + 1 \right )$
.
$O \left (R_1 R_2/\det (\Lambda ) + 1 \right )$
.
Proof If the rectangle
![]() $[-R_1, R_2] \times [-R_2, R_2]$
contains at least two primitive vectors in
$[-R_1, R_2] \times [-R_2, R_2]$
contains at least two primitive vectors in
![]() $\Lambda $
, say
$\Lambda $
, say
![]() ${\mathbf {x}}_1, {\mathbf {x}}_2$
, then since this rectangle is convex it contains the parallelogram with end points
${\mathbf {x}}_1, {\mathbf {x}}_2$
, then since this rectangle is convex it contains the parallelogram with end points
![]() $\pm {\mathbf {x}}_1, \pm {\mathbf {x}}_2$
. The area of this parallelogram is at least as large as
$\pm {\mathbf {x}}_1, \pm {\mathbf {x}}_2$
. The area of this parallelogram is at least as large as
![]() $\det \Lambda $
, since the lattice spanned by
$\det \Lambda $
, since the lattice spanned by
![]() ${\mathbf {x}}_1, {\mathbf {x}}_2$
is a sublattice of
${\mathbf {x}}_1, {\mathbf {x}}_2$
is a sublattice of
![]() $\Lambda $
. It thus follows that
$\Lambda $
. It thus follows that
Otherwise, the rectangle
![]() $[-R_1, R_1] \times [-R_2, R_2]$
contains at most one primitive vector in
$[-R_1, R_1] \times [-R_2, R_2]$
contains at most one primitive vector in
![]() $\Lambda $
. This completes the proof.
$\Lambda $
. This completes the proof.
The strength of this lemma is that it gives a strong upper bound even in lopsided boxes.
Given (7.4), it follows that there is at least one
![]() $i \in \{2,3\}$
such that
$i \in \{2,3\}$
such that
whence
 $$\begin{align*}\frac{x_1 y_1^2}{2 y_i^{-2}} \leq |x_i| \leq \frac{2 x_1 y_1^2}{ y_i^{2}}.\end{align*}$$
$$\begin{align*}\frac{x_1 y_1^2}{2 y_i^{-2}} \leq |x_i| \leq \frac{2 x_1 y_1^2}{ y_i^{2}}.\end{align*}$$
Without loss of generality, we assume that this holds for
![]() $i = 2$
. Suppose that
$i = 2$
. Suppose that
![]() $M_1 \leq x_1 < 2M_1$
. By (7.5), we have
$M_1 \leq x_1 < 2M_1$
. By (7.5), we have
whence
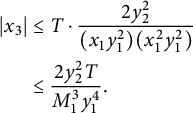 $$ \begin{align*} |x_3| & \leq T \cdot \frac{2 y_2^2}{(x_1 y_1^2)(x_1^2 y_1^2)} \\ & \leq \frac{2y_2^2 T}{M_1^3 y_1^4}. \end{align*} $$
$$ \begin{align*} |x_3| & \leq T \cdot \frac{2 y_2^2}{(x_1 y_1^2)(x_1^2 y_1^2)} \\ & \leq \frac{2y_2^2 T}{M_1^3 y_1^4}. \end{align*} $$
Applying Lemma 7.1 to the lattice defined by the congruence
![]() $y_1^2 x_1 - y_3^2 x_3 \equiv 0 \pmod {y_2^2}$
which has determinant equal to
$y_1^2 x_1 - y_3^2 x_3 \equiv 0 \pmod {y_2^2}$
which has determinant equal to
![]() $y_2^2$
, there are
$y_2^2$
, there are
 $$\begin{align*}O \left(M_1 \cdot \frac{T y_2^2}{M_1^3 y_1^4} \cdot \frac{1}{y_2^2} + 1 \right) = O \left(\frac{T}{M_1^2 y_1^4} + 1 \right)\end{align*}$$
$$\begin{align*}O \left(M_1 \cdot \frac{T y_2^2}{M_1^3 y_1^4} \cdot \frac{1}{y_2^2} + 1 \right) = O \left(\frac{T}{M_1^2 y_1^4} + 1 \right)\end{align*}$$
possibilities for
![]() $x_1, x_3$
, which then determines
$x_1, x_3$
, which then determines
![]() $x_2 = (y_1^2 x_1 - y_3^2 x_3)/y_2^2$
. Similarly, applying Lemma 7.1 to the lattice defined by
$x_2 = (y_1^2 x_1 - y_3^2 x_3)/y_2^2$
. Similarly, applying Lemma 7.1 to the lattice defined by
![]() $y_1^2 x_1 + y_2^2 x_2 \equiv 0 \pmod {y_3^2}$
, with determinant equal to
$y_1^2 x_1 + y_2^2 x_2 \equiv 0 \pmod {y_3^2}$
, with determinant equal to
![]() $y_3^2$
, gives the estimate
$y_3^2$
, gives the estimate
 $$\begin{align*}O \left(M_1 \cdot \frac{y_1^2 M_1}{y_2^2} \frac{1}{y_3^2} + 1\right) = O \left(\frac{M_1^2 y_1^2}{y_2^2 y_3^2} + 1 \right) \end{align*}$$
$$\begin{align*}O \left(M_1 \cdot \frac{y_1^2 M_1}{y_2^2} \frac{1}{y_3^2} + 1\right) = O \left(\frac{M_1^2 y_1^2}{y_2^2 y_3^2} + 1 \right) \end{align*}$$
for the number of
![]() $x_1, x_2$
, which then also determine
$x_1, x_2$
, which then also determine
![]() $x_3$
. The two bounds coincide when
$x_3$
. The two bounds coincide when
 $$\begin{align*}M_1 = \frac{T^{1/4} |y_2 y_3|^{1/2}}{|y_1|^{3/2}}, \end{align*}$$
$$\begin{align*}M_1 = \frac{T^{1/4} |y_2 y_3|^{1/2}}{|y_1|^{3/2}}, \end{align*}$$
and we get the bound
 $$\begin{align*}O \left(\frac{T^{1/2} |y_2 y_3| y_1^2}{y_2^2 y_3^2 |y_1|^3} + 1 \right) = O \left(\frac{T^{1/2}}{|y_1 y_2 y_3|} + 1\right) \end{align*}$$
$$\begin{align*}O \left(\frac{T^{1/2} |y_2 y_3| y_1^2}{y_2^2 y_3^2 |y_1|^3} + 1 \right) = O \left(\frac{T^{1/2}}{|y_1 y_2 y_3|} + 1\right) \end{align*}$$
for the number of
![]() $x_1, x_2, x_3$
given
$x_1, x_2, x_3$
given
![]() $y_1, y_2, y_3$
. Thus, we obtain an acceptable estimate whenever
$y_1, y_2, y_3$
. Thus, we obtain an acceptable estimate whenever
![]() $|y_1 y_2 y_3| \ll T^{1/2}$
, since
$|y_1 y_2 y_3| \ll T^{1/2}$
, since
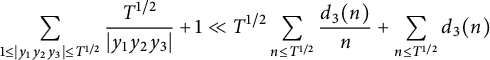 $$ \begin{align*} \sum_{1 \leq |y_1 y_2 y_3| \leq T^{1/2}} \frac{T^{1/2}}{|y_1 y_2 y_3|} + 1 & \ll T^{1/2} \sum_{n \leq T^{1/2}} \frac{d_3(n)}{n} + \sum_{n \leq T^{1/2}} d_3(n) \end{align*} $$
$$ \begin{align*} \sum_{1 \leq |y_1 y_2 y_3| \leq T^{1/2}} \frac{T^{1/2}}{|y_1 y_2 y_3|} + 1 & \ll T^{1/2} \sum_{n \leq T^{1/2}} \frac{d_3(n)}{n} + \sum_{n \leq T^{1/2}} d_3(n) \end{align*} $$
It is well known that
By partial summation, we have
 $$ \begin{align*} \sum_{n \leq Z} \frac{d_3(n)}{n} & = Z^{-1} \sum_{n \leq Z} d_3(n) + \int_1^Z \left(\sum_{n \leq t} d_3(n) \right) \frac{dt}{t^2} \\ & \ll (\log Z)^2 + \int_1^Z \frac{(\log t)^2 dt}{t} \\ & \ll (\log Z)^3. \end{align*} $$
$$ \begin{align*} \sum_{n \leq Z} \frac{d_3(n)}{n} & = Z^{-1} \sum_{n \leq Z} d_3(n) + \int_1^Z \left(\sum_{n \leq t} d_3(n) \right) \frac{dt}{t^2} \\ & \ll (\log Z)^2 + \int_1^Z \frac{(\log t)^2 dt}{t} \\ & \ll (\log Z)^3. \end{align*} $$
It follows that
 $$\begin{align*}T^{1/2} \sum_{n \leq T^{1/2}} \frac{d_3(n)}{n} + \sum_{n \leq T^{1/2}} d_3(n) \ll T^{1/2} (\log T)^3.\end{align*}$$
$$\begin{align*}T^{1/2} \sum_{n \leq T^{1/2}} \frac{d_3(n)}{n} + \sum_{n \leq T^{1/2}} d_3(n) \ll T^{1/2} (\log T)^3.\end{align*}$$
It remains to deal with the case when
![]() $|y_1 y_2 y_3| \gg T^{1/2}$
, where we instead fiber over
$|y_1 y_2 y_3| \gg T^{1/2}$
, where we instead fiber over
![]() ${\mathbf {x}}$
and consider zeros of the corresponding diagonal quadratic forms
${\mathbf {x}}$
and consider zeros of the corresponding diagonal quadratic forms
![]() $Q_{\mathbf {x}}$
. Since
$Q_{\mathbf {x}}$
. Since
for
![]() $i = 1,2$
by assumption, it follows that
$i = 1,2$
by assumption, it follows that
hence,
 $$\begin{align*}|y_1^2 y_2^2 y_3^2| \ll \frac{x_1^3 y_1^6}{x_1 |x_2 x_3|}.\end{align*}$$
$$\begin{align*}|y_1^2 y_2^2 y_3^2| \ll \frac{x_1^3 y_1^6}{x_1 |x_2 x_3|}.\end{align*}$$
If
![]() $|x_1 x_2 x_3| \gg T^{1/2}$
, then
$|x_1 x_2 x_3| \gg T^{1/2}$
, then
This implies that
which violates (7.5) if the implied constants are sufficiently large. It thus follows that we must have
![]() $|x_1 x_2 x_3| \ll T^{1/2}$
in this case.
$|x_1 x_2 x_3| \ll T^{1/2}$
in this case.
We now fix
![]() $x_1, x_2, x_3$
and consider (7.4) as a ternary quadratic form in
$x_1, x_2, x_3$
and consider (7.4) as a ternary quadratic form in
![]() $y_1, y_2, y_3$
. We shall require the following version of Corollary 2 in [Reference Browning and Heath-Brown3], which is an analogue of Lemma 7.1.
$y_1, y_2, y_3$
. We shall require the following version of Corollary 2 in [Reference Browning and Heath-Brown3], which is an analogue of Lemma 7.1.
Lemma 7.2 Let
![]() $x_1, x_2, x_3$
be pairwise co-prime square-free integers. Let
$x_1, x_2, x_3$
be pairwise co-prime square-free integers. Let
![]() $R_1, R_2, R_3$
be positive real numbers. Then the number of primitive solutions
$R_1, R_2, R_3$
be positive real numbers. Then the number of primitive solutions
![]() $y_1, y_2, y_3$
to the equation
$y_1, y_2, y_3$
to the equation
with
![]() $|y_i| \leq R_i$
is bounded by
$|y_i| \leq R_i$
is bounded by
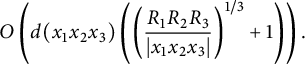 $$\begin{align*}O \left( d(x_1 x_2 x_3) \left( \left(\frac{R_1 R_2 R_3}{|x_1 x_2 x_3|} \right)^{1/3} + 1 \right) \right).\end{align*}$$
$$\begin{align*}O \left( d(x_1 x_2 x_3) \left( \left(\frac{R_1 R_2 R_3}{|x_1 x_2 x_3|} \right)^{1/3} + 1 \right) \right).\end{align*}$$
Since
![]() $|x_i y_i^2| \ll x_1 y_1^2$
for
$|x_i y_i^2| \ll x_1 y_1^2$
for
![]() $i = 1,2$
, it follows that
$i = 1,2$
, it follows that
for
![]() $i = 1,2$
, whence
$i = 1,2$
, whence
This implies that
hence
 $$\begin{align*}|y_1 y_2 y_3| \ll \frac{T^{3/2}}{(x_1 x_2 x_3)^2}.\end{align*}$$
$$\begin{align*}|y_1 y_2 y_3| \ll \frac{T^{3/2}}{(x_1 x_2 x_3)^2}.\end{align*}$$
Lemma 7.2 then implies that for fixed
![]() $x_1, x_2, x_3$
, the number of primitive
$x_1, x_2, x_3$
, the number of primitive
![]() ${\mathbf {y}} = (y_1, y_2, y_3)$
satisfying (7.4) is
${\mathbf {y}} = (y_1, y_2, y_3)$
satisfying (7.4) is
 $$\begin{align*}O \left(d(x_1 x_2 x_3) \left(\frac{T^{1/2}}{|x_1 x_2 x_3|} + 1 \right) \right). \end{align*}$$
$$\begin{align*}O \left(d(x_1 x_2 x_3) \left(\frac{T^{1/2}}{|x_1 x_2 x_3|} + 1 \right) \right). \end{align*}$$
We now sum over primitive
![]() ${\mathbf {x}} \in {\mathbb {Z}}^3$
satisfying
${\mathbf {x}} \in {\mathbb {Z}}^3$
satisfying
![]() $|x_1 x_2 x_3| \ll T^{1/2}$
, with the property that the quadratic form
$|x_1 x_2 x_3| \ll T^{1/2}$
, with the property that the quadratic form
![]() $Q_{\mathbf {x}}$
given by (7.4) has a rational zero. By the Hasse–Minkowski theorem, this is tantamount to the form
$Q_{\mathbf {x}}$
given by (7.4) has a rational zero. By the Hasse–Minkowski theorem, this is tantamount to the form
![]() $Q_{\mathbf {x}}({\mathbf {y}}) = x_1 y_1^2 + x_2 y_2^2 - x_3 y_3^2$
being everywhere locally soluble. The estimation of this is interesting on its own right and will be handled in a separate subsection.
$Q_{\mathbf {x}}({\mathbf {y}}) = x_1 y_1^2 + x_2 y_2^2 - x_3 y_3^2$
being everywhere locally soluble. The estimation of this is interesting on its own right and will be handled in a separate subsection.
7.2.2 Counting soluble ternary quadratic forms
In this section, we consider the set
 $$\begin{align*}{\mathcal{S}} = &\{(x_1, x_2, x_3) \in {\mathbb{Z}}^3 : x_1, x_2, x_3> 0, \gcd(x_1, x_2) = \gcd(x_1, x_3) = \gcd(x_2, x_3) = 1,\\& \quad x_i \text{ square-free for } i = 1,2,3, x_1 y_1^2 + x_2 y_2^2 - x_3 y_3^2 \text{ is everywhere locally soluble}\}. \end{align*}$$
$$\begin{align*}{\mathcal{S}} = &\{(x_1, x_2, x_3) \in {\mathbb{Z}}^3 : x_1, x_2, x_3> 0, \gcd(x_1, x_2) = \gcd(x_1, x_3) = \gcd(x_2, x_3) = 1,\\& \quad x_i \text{ square-free for } i = 1,2,3, x_1 y_1^2 + x_2 y_2^2 - x_3 y_3^2 \text{ is everywhere locally soluble}\}. \end{align*}$$
By a well-known theorem of Legendre (see [Reference Guo12]), the indicator function for
![]() ${\mathcal {S}}$
is given by
${\mathcal {S}}$
is given by
 $$ \begin{align} f_{\mathcal{S}}(x_1, x_2, x_3) = \left(2^{-\omega(x_1)} \sum_{a_1 | x_1} \left(\frac{x_2 x_3}{a_1} \right) \right) \left(2^{-\omega(x_2)} \sum_{a_2 | x_2} \left(\frac{x_1 x_3}{a_2} \right) \right) \left(2^{-\omega(x_3)} \sum_{a_3 | x_3} \left(\frac{-x_1 x_2}{a_3} \right) \right). \end{align} $$
$$ \begin{align} f_{\mathcal{S}}(x_1, x_2, x_3) = \left(2^{-\omega(x_1)} \sum_{a_1 | x_1} \left(\frac{x_2 x_3}{a_1} \right) \right) \left(2^{-\omega(x_2)} \sum_{a_2 | x_2} \left(\frac{x_1 x_3}{a_2} \right) \right) \left(2^{-\omega(x_3)} \sum_{a_3 | x_3} \left(\frac{-x_1 x_2}{a_3} \right) \right). \end{align} $$
We will now combine the ideas given in [Reference Guo12] and those in [Reference Fouvry and Kluners8].
Put
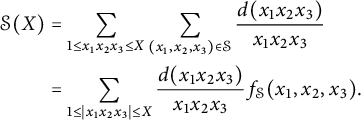 $$ \begin{align*} {\mathcal{S}}(X) & = \sum_{1 \leq x_1 x_2 x_3 \leq X} \sum_{(x_1, x_2, x_3) \in {\mathcal{S}}} \frac{d(x_1 x_2 x_3)}{x_1 x_2 x_3} \\ & = \sum_{1 \leq |x_1 x_2 x_3| \leq X} \frac{d(x_1 x_2 x_3)}{x_1 x_2 x_3} f_{\mathcal{S}}(x_1, x_2, x_3). \end{align*} $$
$$ \begin{align*} {\mathcal{S}}(X) & = \sum_{1 \leq x_1 x_2 x_3 \leq X} \sum_{(x_1, x_2, x_3) \in {\mathcal{S}}} \frac{d(x_1 x_2 x_3)}{x_1 x_2 x_3} \\ & = \sum_{1 \leq |x_1 x_2 x_3| \leq X} \frac{d(x_1 x_2 x_3)}{x_1 x_2 x_3} f_{\mathcal{S}}(x_1, x_2, x_3). \end{align*} $$
Since
![]() $x_1, x_2, x_3$
are pairwise coprime and square-free, it follows that
$x_1, x_2, x_3$
are pairwise coprime and square-free, it follows that
where
![]() $\omega (n)$
is the number of distinct prime factors of n. It follows that
$\omega (n)$
is the number of distinct prime factors of n. It follows that
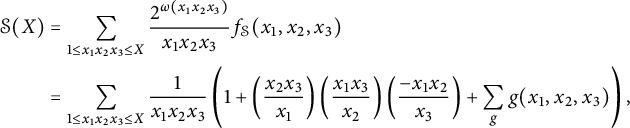 $$ \begin{align} {\mathcal{S}}(X) &= \sum_{1 \leq x_1 x_2 x_3 \leq X} \frac{2^{\omega(x_1 x_2 x_3)}}{x_1 x_2 x_3} f_{\mathcal{S}}(x_1, x_2, x_3)\\&= \sum_{1 \leq x_1 x_2 x_3 \leq X} \frac{1}{x_1 x_2 x_3} \left(1 + \left(\frac{x_2 x_3}{x_1} \right) \left(\frac{x_1 x_3}{x_2} \right) \left(\frac{-x_1 x_2}{x_3} \right) + \sum_g g(x_1, x_2, x_3)\right),\nonumber \end{align} $$
$$ \begin{align} {\mathcal{S}}(X) &= \sum_{1 \leq x_1 x_2 x_3 \leq X} \frac{2^{\omega(x_1 x_2 x_3)}}{x_1 x_2 x_3} f_{\mathcal{S}}(x_1, x_2, x_3)\\&= \sum_{1 \leq x_1 x_2 x_3 \leq X} \frac{1}{x_1 x_2 x_3} \left(1 + \left(\frac{x_2 x_3}{x_1} \right) \left(\frac{x_1 x_3}{x_2} \right) \left(\frac{-x_1 x_2}{x_3} \right) + \sum_g g(x_1, x_2, x_3)\right),\nonumber \end{align} $$
where g expresses a product of Jacobi symbols. The sum
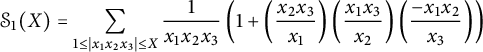 $$ \begin{align} {\mathcal{S}}_1(X) = \sum_{1 \leq |x_1 x_2 x_3| \leq X} \frac{1}{x_1 x_2 x_3} \left(1 + \left(\frac{x_2 x_3}{x_1} \right) \left(\frac{x_1 x_3}{x_2} \right) \left(\frac{-x_1 x_2}{x_3} \right) \right) \end{align} $$
$$ \begin{align} {\mathcal{S}}_1(X) = \sum_{1 \leq |x_1 x_2 x_3| \leq X} \frac{1}{x_1 x_2 x_3} \left(1 + \left(\frac{x_2 x_3}{x_1} \right) \left(\frac{x_1 x_3}{x_2} \right) \left(\frac{-x_1 x_2}{x_3} \right) \right) \end{align} $$
is expected to contribute the main term, while the sum
 $$ \begin{align} {\mathcal{S}}_2(x) = \sum_{1 \leq x_1 x_2 x_3 \leq X} \frac{1}{x_1 x_2 x_3} \sum_g g(x_1, x_2, x_3) \end{align} $$
$$ \begin{align} {\mathcal{S}}_2(x) = \sum_{1 \leq x_1 x_2 x_3 \leq X} \frac{1}{x_1 x_2 x_3} \sum_g g(x_1, x_2, x_3) \end{align} $$
is expected to be negligible, due to the cancellation of characters.
By partial summation, we obtain
where
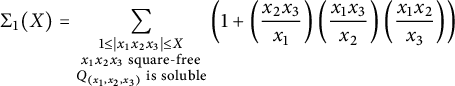 $$\begin{align*}\Sigma_1(X) = \sum_{\substack{1 \leq |x_1 x_2 x_3| \leq X \\ x_1 x_2 x_3 \text{ square-free} \\ Q_{(x_1, x_2, x_3)} \text{ is soluble} }} \left(1 + \left(\frac{x_2 x_3}{x_1} \right) \left(\frac{x_1 x_3}{x_2} \right) \left(\frac{x_1 x_2}{x_3} \right) \right) \end{align*}$$
$$\begin{align*}\Sigma_1(X) = \sum_{\substack{1 \leq |x_1 x_2 x_3| \leq X \\ x_1 x_2 x_3 \text{ square-free} \\ Q_{(x_1, x_2, x_3)} \text{ is soluble} }} \left(1 + \left(\frac{x_2 x_3}{x_1} \right) \left(\frac{x_1 x_3}{x_2} \right) \left(\frac{x_1 x_2}{x_3} \right) \right) \end{align*}$$
and
Our situation differs from that of Guo in [Reference Guo12] since we are counting over triples with
![]() $|x_1 x_2 x_3| \leq X$
rather than
$|x_1 x_2 x_3| \leq X$
rather than
![]() $\max \{|x_1|, |x_2|, |x_3|\} \leq X$
, which introduces some difficulties. However, this is exactly analogous to the situation encountered by Fouvry and Kluners in [Reference Fouvry and Kluners8].
$\max \{|x_1|, |x_2|, |x_3|\} \leq X$
, which introduces some difficulties. However, this is exactly analogous to the situation encountered by Fouvry and Kluners in [Reference Fouvry and Kluners8].
Our key proposition will be the following.
Proposition 7.3 We have the asymptotic upper bound
In fact, we can refine Proposition 7.3 to give an asymptotic formula, but this is unnecessary for our purposes.
We proceed to prove Proposition 7.3 in the remainder of the section. We begin by showing that triples
![]() $(x_1, x_2, x_3)$
with
$(x_1, x_2, x_3)$
with
![]() $\mu ^2(x_1 x_2 x_3) = 1$
and
$\mu ^2(x_1 x_2 x_3) = 1$
and
![]() $\omega (x_1 x_2 x_3)$
large contribute negligibly. To wit, put
$\omega (x_1 x_2 x_3)$
large contribute negligibly. To wit, put
 $$\begin{align*}{\mathcal{S}}_2^{(r)}(X) = \sum_{\substack{1 \leq x_1 x_2 x_3 \leq X \\ \omega(x_1 x_2 x_3) = r}} \frac{1}{x_1 x_2 x_3} \sum_g g(x_1, x_2, x_3).\end{align*}$$
$$\begin{align*}{\mathcal{S}}_2^{(r)}(X) = \sum_{\substack{1 \leq x_1 x_2 x_3 \leq X \\ \omega(x_1 x_2 x_3) = r}} \frac{1}{x_1 x_2 x_3} \sum_g g(x_1, x_2, x_3).\end{align*}$$
By the triangle inequality, it is clear that
 $$\begin{align*}\left \lvert {\mathcal{S}}_2^{(r)}(X) \right \rvert \ll \sum_{\substack{n \leq X \\ \mu^2(n) = 1, \omega(n) = r}} \frac{d_3(n)}{n}. \end{align*}$$
$$\begin{align*}\left \lvert {\mathcal{S}}_2^{(r)}(X) \right \rvert \ll \sum_{\substack{n \leq X \\ \mu^2(n) = 1, \omega(n) = r}} \frac{d_3(n)}{n}. \end{align*}$$
By partial summation, we have
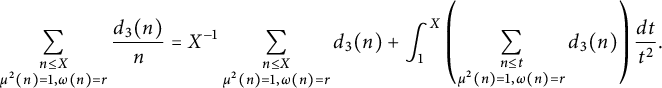 $$\begin{align*}\sum_{\substack{n \leq X \\ \mu^2(n) = 1, \omega(n) = r}} \frac{d_3(n)}{n} = X^{-1} \sum_{\substack{n \leq X \\ \mu^2(n) = 1, \omega(n) = r}} d_3(n) + \int_1^X \left(\sum_{\substack{n \leq t \\ \mu^2(n) = 1, \omega(n) = r}} d_3(n) \right)\frac{dt}{t^2}. \end{align*}$$
$$\begin{align*}\sum_{\substack{n \leq X \\ \mu^2(n) = 1, \omega(n) = r}} \frac{d_3(n)}{n} = X^{-1} \sum_{\substack{n \leq X \\ \mu^2(n) = 1, \omega(n) = r}} d_3(n) + \int_1^X \left(\sum_{\substack{n \leq t \\ \mu^2(n) = 1, \omega(n) = r}} d_3(n) \right)\frac{dt}{t^2}. \end{align*}$$
To estimate the latter sum, we will need the following result, which is Lemma 11 in [Reference Fouvry and Kluners8].
Lemma 7.4 There exists an absolute constant
![]() $B_0 \geq 1$
such that for every
$B_0 \geq 1$
such that for every
![]() $r \geq 0$
, we have
$r \geq 0$
, we have
 $$\begin{align*}|\{n \leq X : \omega(n) = r, \mu^2(n) = 1\}| \leq B_0 \cdot \frac{X}{\log X} \cdot \frac{(\log \log X + B_0)^r}{r!}. \end{align*}$$
$$\begin{align*}|\{n \leq X : \omega(n) = r, \mu^2(n) = 1\}| \leq B_0 \cdot \frac{X}{\log X} \cdot \frac{(\log \log X + B_0)^r}{r!}. \end{align*}$$
Applying the lemma, we have for
![]() $\Omega = 30 (\log \log X + B_0)$
$\Omega = 30 (\log \log X + B_0)$
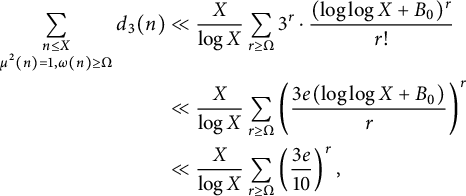 $$ \begin{align*} \sum_{\substack{n \leq X \\ \mu^2(n) = 1, \omega(n) \geq \Omega}} d_3(n) & \ll \frac{X}{\log X} \sum_{r \geq \Omega} 3^r \cdot \frac{(\log \log X + B_0)^r}{r!} \\ & \ll \frac{X}{\log X} \sum_{r \geq \Omega} \left(\frac{3e (\log \log X + B_0)}{r} \right)^r \\ & \ll \frac{X}{\log X} \sum_{r \geq \Omega} \left(\frac{3e}{10} \right)^r, \end{align*} $$
$$ \begin{align*} \sum_{\substack{n \leq X \\ \mu^2(n) = 1, \omega(n) \geq \Omega}} d_3(n) & \ll \frac{X}{\log X} \sum_{r \geq \Omega} 3^r \cdot \frac{(\log \log X + B_0)^r}{r!} \\ & \ll \frac{X}{\log X} \sum_{r \geq \Omega} \left(\frac{3e (\log \log X + B_0)}{r} \right)^r \\ & \ll \frac{X}{\log X} \sum_{r \geq \Omega} \left(\frac{3e}{10} \right)^r, \end{align*} $$
the final sum a convergent geometric series. Hence,
 $$\begin{align*}\sum_{r \geq \Omega} \left(\frac{3e}{10} \right)^r \ll \left(\frac{3e}{10} \right)^{\Omega} \ll \frac{1}{\log X}. \end{align*}$$
$$\begin{align*}\sum_{r \geq \Omega} \left(\frac{3e}{10} \right)^r \ll \left(\frac{3e}{10} \right)^{\Omega} \ll \frac{1}{\log X}. \end{align*}$$
We thus conclude that
 $$ \begin{align} \sum_{r \geq \Omega} \left \lvert S_2^{(r)}(X) \right \rvert & \ll 1 + (\log X)^{-2} + \int_1^X \frac{dt}{t (\log t)^2} \\ & = O(1) \notag \end{align} $$
$$ \begin{align} \sum_{r \geq \Omega} \left \lvert S_2^{(r)}(X) \right \rvert & \ll 1 + (\log X)^{-2} + \int_1^X \frac{dt}{t (\log t)^2} \\ & = O(1) \notag \end{align} $$
and is thus negligible.
Note that
![]() $x_1, x_2, -x_3$
cannot all be the same sign; otherwise, (7.4) will only have a trivial real solution. Hence, the signs of
$x_1, x_2, -x_3$
cannot all be the same sign; otherwise, (7.4) will only have a trivial real solution. Hence, the signs of
![]() $(x_1, x_2, x_3)$
must be
$(x_1, x_2, x_3)$
must be
![]() $(+, +, +)$
, or
$(+, +, +)$
, or
![]() $(+, -, +)$
, since we assumed
$(+, -, +)$
, since we assumed
![]() $x_1> 0$
and
$x_1> 0$
and
![]() $x_1 y_1^2 \geq |x_2 y_2^2|$
. By rearranging, we must thus assume
$x_1 y_1^2 \geq |x_2 y_2^2|$
. By rearranging, we must thus assume
![]() $x_1, x_2, x_3> 0$
.
$x_1, x_2, x_3> 0$
.
We then expand (7.11) by writing
![]() $x_i = x_{i1}x_{i2}$
for
$x_i = x_{i1}x_{i2}$
for
![]() $i = 1,2,3$
, and
$i = 1,2,3$
, and
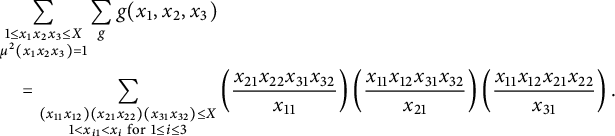 $$\begin{align*}&\sum_{\substack{1 \leq x_1 x_2 x_3 \leq X \\ \mu^2(x_1 x_2 x_3) = 1}} \sum_g g(x_1, x_2, x_3)\\& \quad = \sum_{\substack{(x_{11}x_{12})(x_{21}x_{22})(x_{31}x_{32})\leq X \\ 1 < x_{i1} < x_i \text{ for } 1 \leq i \leq 3}} \left(\frac{x_{21}x_{22} x_{31}x_{32} }{x_{11}} \right) \left( \frac{x_{11} x_{12} x_{31} x_{32}}{x_{21}} \right) \left(\frac{x_{11} x_{12} x_{21} x_{22}}{x_{31}} \right). \end{align*}$$
$$\begin{align*}&\sum_{\substack{1 \leq x_1 x_2 x_3 \leq X \\ \mu^2(x_1 x_2 x_3) = 1}} \sum_g g(x_1, x_2, x_3)\\& \quad = \sum_{\substack{(x_{11}x_{12})(x_{21}x_{22})(x_{31}x_{32})\leq X \\ 1 < x_{i1} < x_i \text{ for } 1 \leq i \leq 3}} \left(\frac{x_{21}x_{22} x_{31}x_{32} }{x_{11}} \right) \left( \frac{x_{11} x_{12} x_{31} x_{32}}{x_{21}} \right) \left(\frac{x_{11} x_{12} x_{21} x_{22}}{x_{31}} \right). \end{align*}$$
We now follow the strategy outlined in [Reference Fouvry and Kluners8] and break up the set
by restricting the
![]() $x_{ij}$
’s to intervals of the form
$x_{ij}$
’s to intervals of the form
where
For a given
![]() $\mathbf {A} = (A_{11}, A_{12}, A_{21}, A_{22}, A_{31}, A_{32})$
, put
$\mathbf {A} = (A_{11}, A_{12}, A_{21}, A_{22}, A_{31}, A_{32})$
, put
 $$\begin{align*}{\mathcal{S}}_2(X; \mathbf{A}) = \sum_{\substack{x_{ij} \in [A_{ij}, \Delta A_{ij}) \\ \mu^2(x_{11} x_{12} x_{21} x_{22} x_{31} x_{32}) = 1 \\ \prod_{i,j} x_{ij} \leq X }} \left(\frac{x_{21}x_{22} x_{31}x_{32} }{x_{11}} \right) \left( \frac{x_{11} x_{12} x_{31} x_{32}}{x_{21}} \right) \left(\frac{x_{11} x_{12} x_{21} x_{22}}{x_{31}} \right). \end{align*}$$
$$\begin{align*}{\mathcal{S}}_2(X; \mathbf{A}) = \sum_{\substack{x_{ij} \in [A_{ij}, \Delta A_{ij}) \\ \mu^2(x_{11} x_{12} x_{21} x_{22} x_{31} x_{32}) = 1 \\ \prod_{i,j} x_{ij} \leq X }} \left(\frac{x_{21}x_{22} x_{31}x_{32} }{x_{11}} \right) \left( \frac{x_{11} x_{12} x_{31} x_{32}}{x_{21}} \right) \left(\frac{x_{11} x_{12} x_{21} x_{22}}{x_{31}} \right). \end{align*}$$
We then have the following lemma.
Lemma 7.5 We have the bound
Proof We have
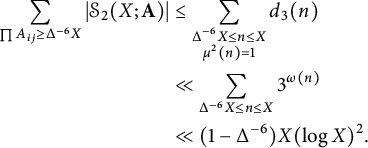 $$ \begin{align*} \sum_{\prod A_{ij} \geq \Delta^{-6} X} \left \lvert {\mathcal{S}}_2(X; \mathbf{A}) \right \rvert & \leq \sum_{\substack{\Delta^{-6} X \leq n \leq X \\ \mu^2(n) = 1}} d_3(n) \\ & \ll \sum_{\Delta^{-6} X \leq n \leq X} 3^{\omega(n)} \\ & \ll (1 - \Delta^{-6} ) X (\log X)^2. \end{align*} $$
$$ \begin{align*} \sum_{\prod A_{ij} \geq \Delta^{-6} X} \left \lvert {\mathcal{S}}_2(X; \mathbf{A}) \right \rvert & \leq \sum_{\substack{\Delta^{-6} X \leq n \leq X \\ \mu^2(n) = 1}} d_3(n) \\ & \ll \sum_{\Delta^{-6} X \leq n \leq X} 3^{\omega(n)} \\ & \ll (1 - \Delta^{-6} ) X (\log X)^2. \end{align*} $$
By Taylor’s theorem, we have
The proof then follows.
To proceed, we shall require the following well-known lemma regarding character sums.
Lemma 7.6 (Double Oscillation Lemma)
Let
![]() $\{\alpha _n\}, \{\beta _m\}$
be two sequences of complex numbers with each term having absolute value bounded by
$\{\alpha _n\}, \{\beta _m\}$
be two sequences of complex numbers with each term having absolute value bounded by
![]() $1$
. Let
$1$
. Let
![]() $M,N$
be positive real numbers. Then we have
$M,N$
be positive real numbers. Then we have
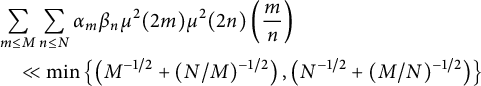 $$\begin{align*}&\sum_{m \leq M} \sum_{n \leq N} \alpha_m \beta_n \mu^2(2m) \mu^2(2n) \left(\frac{m}{n} \right)\\& \quad \ll \min \left\{ \left(M^{-1/2} + (N/M)^{-1/2} \right), \left(N^{-1/2} + (M/N)^{-1/2} \right) \right\} \end{align*}$$
$$\begin{align*}&\sum_{m \leq M} \sum_{n \leq N} \alpha_m \beta_n \mu^2(2m) \mu^2(2n) \left(\frac{m}{n} \right)\\& \quad \ll \min \left\{ \left(M^{-1/2} + (N/M)^{-1/2} \right), \left(N^{-1/2} + (M/N)^{-1/2} \right) \right\} \end{align*}$$
and for every
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
We will also need the following variant of the Siegel–Walfisz theorem.
Lemma 7.7 Let
![]() $\chi _q$
be a primitive character modulo
$\chi _q$
be a primitive character modulo
![]() $q \geq 2$
. Then, for every
$q \geq 2$
. Then, for every
![]() $A> 1$
, we have
$A> 1$
, we have
uniformly for
![]() $X \geq Y \geq 2$
.
$X \geq Y \geq 2$
.
We now consider, as in [Reference Fouvry and Kluners8], the quantities
We now consider those
![]() $\mathbf {A}$
with the property that at most two entries larger than
$\mathbf {A}$
with the property that at most two entries larger than
![]() $X^\ddagger $
. We dissect the sum according to the number
$X^\ddagger $
. We dissect the sum according to the number
![]() $r \leq 2$
of terms
$r \leq 2$
of terms
![]() $A_{ij}$
greater than
$A_{ij}$
greater than
![]() $X^\ddagger $
. Let n be the product of those
$X^\ddagger $
. Let n be the product of those
![]() $x_{ij}$
which are larger than
$x_{ij}$
which are larger than
![]() $X^\ddagger $
, and m the product of the remaining ones. We sum over
$X^\ddagger $
, and m the product of the remaining ones. We sum over
![]() $\mathbf {A}$
with such properties to obtain
$\mathbf {A}$
with such properties to obtain
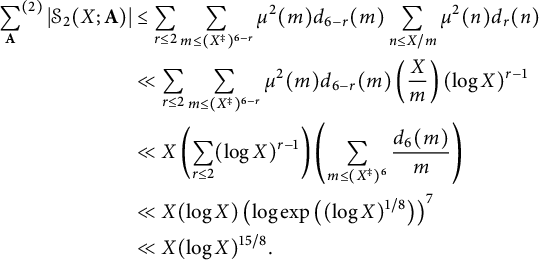 $$ \begin{align*} \sideset{}{^{(2)}} \sum_{\mathbf{A}} |{\mathcal{S}}_2(X; \mathbf{A})| & \leq \sum_{r \leq 2} \sum_{m \leq (X^\ddagger)^{6-r}} \mu^2(m) d_{6-r}(m) \sum_{n \leq X/m} \mu^2(n) d_r(n) \\ & \ll \sum_{r \leq 2} \sum_{m \leq (X^\ddagger)^{6-r}} \mu^2(m) d_{6-r}(m) \left(\frac{X}{m} \right) (\log X)^{r-1} \\ & \ll X \left(\sum_{r \leq 2} (\log X)^{r-1} \right) \left(\sum_{m \leq (X^\ddagger)^{6}} \frac{d_{6}(m)}{m} \right) \\ & \ll X (\log X)\left(\log \exp \left((\log X)^{1/8} \right) \right)^7 \\ & \ll X (\log X)^{15/8}. \end{align*} $$
$$ \begin{align*} \sideset{}{^{(2)}} \sum_{\mathbf{A}} |{\mathcal{S}}_2(X; \mathbf{A})| & \leq \sum_{r \leq 2} \sum_{m \leq (X^\ddagger)^{6-r}} \mu^2(m) d_{6-r}(m) \sum_{n \leq X/m} \mu^2(n) d_r(n) \\ & \ll \sum_{r \leq 2} \sum_{m \leq (X^\ddagger)^{6-r}} \mu^2(m) d_{6-r}(m) \left(\frac{X}{m} \right) (\log X)^{r-1} \\ & \ll X \left(\sum_{r \leq 2} (\log X)^{r-1} \right) \left(\sum_{m \leq (X^\ddagger)^{6}} \frac{d_{6}(m)}{m} \right) \\ & \ll X (\log X)\left(\log \exp \left((\log X)^{1/8} \right) \right)^7 \\ & \ll X (\log X)^{15/8}. \end{align*} $$
This is sufficiently small for our purposes.
We may now assume that
![]() $A_{ij} \geq X^\ddagger $
for at least three pairs
$A_{ij} \geq X^\ddagger $
for at least three pairs
![]() $i,j$
with
$i,j$
with
![]() $1 \leq i \leq 3, 1 \leq j \leq 2$
. We now suppose that there exist
$1 \leq i \leq 3, 1 \leq j \leq 2$
. We now suppose that there exist
![]() $a \ne b$
such that
$a \ne b$
such that
The sum over
![]() $\mathbf {A}$
satisfying these properties can be bounded by
$\mathbf {A}$
satisfying these properties can be bounded by
 $$ \begin{align*} \sum_{\mathbf{A}} \left \lvert {\mathcal{S}}_2(X; \mathbf{A}) \right \rvert & \leq \sum_{x_{ij}, (i,j) \ne (a,2), (b,1)} \prod_{(i,j) \ne (a,2), (b,1)} \left \lvert \sum_{x_{a,2}} \sum_{x_{b,1}} \alpha_{(a,2)} \beta_{(b,1)} \left(\frac{x_{a,2}}{x_{b,1}} \right) \right \rvert, \end{align*} $$
$$ \begin{align*} \sum_{\mathbf{A}} \left \lvert {\mathcal{S}}_2(X; \mathbf{A}) \right \rvert & \leq \sum_{x_{ij}, (i,j) \ne (a,2), (b,1)} \prod_{(i,j) \ne (a,2), (b,1)} \left \lvert \sum_{x_{a,2}} \sum_{x_{b,1}} \alpha_{(a,2)} \beta_{(b,1)} \left(\frac{x_{a,2}}{x_{b,1}} \right) \right \rvert, \end{align*} $$
where
![]() $\alpha , \beta $
have modulus at most one. Lemma 7.6 then applies, and since our variables
$\alpha , \beta $
have modulus at most one. Lemma 7.6 then applies, and since our variables
![]() $x_{a,2}, x_{b,1}$
range over intervals exceeding
$x_{a,2}, x_{b,1}$
range over intervals exceeding
![]() $X^\dagger $
in length, it follows that
$X^\dagger $
in length, it follows that
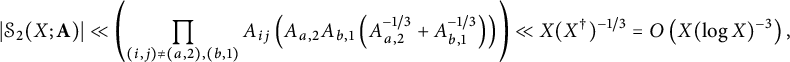 $$\begin{align*}|{\mathcal{S}}_2(X;\mathbf{A})| \ll \left(\prod_{(i,j) \ne (a,2), (b,1)} A_{ij} \left(A_{a,2} A_{b,1} \left(A_{a,2}^{-1/3} + A_{b,1}^{-1/3} \right) \right) \right) \ll X (X^\dagger)^{-1/3} = O \left(X (\log X)^{-3} \right), \end{align*}$$
$$\begin{align*}|{\mathcal{S}}_2(X;\mathbf{A})| \ll \left(\prod_{(i,j) \ne (a,2), (b,1)} A_{ij} \left(A_{a,2} A_{b,1} \left(A_{a,2}^{-1/3} + A_{b,1}^{-1/3} \right) \right) \right) \ll X (X^\dagger)^{-1/3} = O \left(X (\log X)^{-3} \right), \end{align*}$$
which is again enough.
Next, consider the family where the two previous conditions do not hold, and in addition there exist
![]() $a \ne b$
such that
$a \ne b$
such that
![]() $2 \leq A_{b,1} \leq X^\dagger $
and
$2 \leq A_{b,1} \leq X^\dagger $
and
![]() $A_{a,2}> X^\ddagger $
. Under these conditions, we see that
$A_{a,2}> X^\ddagger $
. Under these conditions, we see that
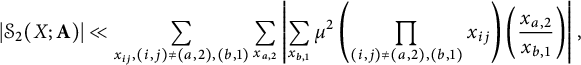 $$\begin{align*}|{\mathcal{S}}_2(X; \mathbf{A})| \ll \sum_{x_{ij}, (i,j) \ne (a,2), (b,1)} \sum_{x_{a,2}} \left \lvert \sum_{x_{b,1}} \mu^2 \left(\prod_{(i,j) \ne (a,2), (b,1)} x_{ij} \right) \left(\frac{x_{a,2}}{x_{b,1}} \right) \right \rvert, \end{align*}$$
$$\begin{align*}|{\mathcal{S}}_2(X; \mathbf{A})| \ll \sum_{x_{ij}, (i,j) \ne (a,2), (b,1)} \sum_{x_{a,2}} \left \lvert \sum_{x_{b,1}} \mu^2 \left(\prod_{(i,j) \ne (a,2), (b,1)} x_{ij} \right) \left(\frac{x_{a,2}}{x_{b,1}} \right) \right \rvert, \end{align*}$$
where
![]() $A_{ij} \leq x_{ij} \leq \Delta A_{ij}$
and
$A_{ij} \leq x_{ij} \leq \Delta A_{ij}$
and
![]() $\omega (x_{ij}) \leq \Omega $
for
$\omega (x_{ij}) \leq \Omega $
for
![]() $1 \leq i \leq 3, 1 \leq j \leq 2$
. Now put
$1 \leq i \leq 3, 1 \leq j \leq 2$
. Now put
![]() $\ell = \omega (x_{a,2})$
, writing
$\ell = \omega (x_{a,2})$
, writing
with
![]() $p_1 < p_2 < \cdots < p_\ell $
, we obtain
$p_1 < p_2 < \cdots < p_\ell $
, we obtain
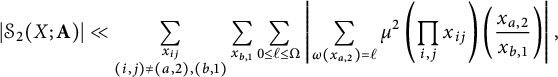 $$\begin{align*}|{\mathcal{S}}_2(X; \mathbf{A})| \ll \sum_{\substack{x_{ij} \\ (i,j) \ne (a,2), (b,1)}} \sum_{x_{b,1}} \sum_{0 \leq \ell \leq \Omega} \left \lvert \sum_{\omega(x_{a,2}) = \ell} \mu^2\left(\prod_{i,j} x_{ij} \right) \left(\frac{x_{a,2}}{x_{b,1}} \right) \right \rvert,\end{align*}$$
$$\begin{align*}|{\mathcal{S}}_2(X; \mathbf{A})| \ll \sum_{\substack{x_{ij} \\ (i,j) \ne (a,2), (b,1)}} \sum_{x_{b,1}} \sum_{0 \leq \ell \leq \Omega} \left \lvert \sum_{\omega(x_{a,2}) = \ell} \mu^2\left(\prod_{i,j} x_{ij} \right) \left(\frac{x_{a,2}}{x_{b,1}} \right) \right \rvert,\end{align*}$$
the inner sum being bounded by
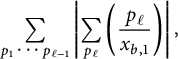 $$\begin{align*}\sum_{p_1 \cdots p_{\ell-1}} \left \lvert \sum_{p_\ell} \left(\frac{p_\ell}{x_{b,1}} \right) \right \rvert, \end{align*}$$
$$\begin{align*}\sum_{p_1 \cdots p_{\ell-1}} \left \lvert \sum_{p_\ell} \left(\frac{p_\ell}{x_{b,1}} \right) \right \rvert, \end{align*}$$
and
![]() $p_1, \ldots , p_\ell $
satisfy
$p_1, \ldots , p_\ell $
satisfy
![]() $A_{a,2} \leq p_1 \cdots p_{\ell } \leq \Delta A_{a,2}$
. Note that
$A_{a,2} \leq p_1 \cdots p_{\ell } \leq \Delta A_{a,2}$
. Note that
We may now apply Lemma 7.7 to obtain the bound
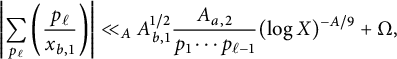 $$\begin{align*}\left \lvert \sum_{p_\ell} \left(\frac{p_\ell}{x_{b,1}} \right) \right \rvert \ll_A A_{b,1}^{1/2} \frac{A_{a,2}}{p_1 \cdots p_{\ell-1}} (\log X)^{-A/9} + \Omega, \end{align*}$$
$$\begin{align*}\left \lvert \sum_{p_\ell} \left(\frac{p_\ell}{x_{b,1}} \right) \right \rvert \ll_A A_{b,1}^{1/2} \frac{A_{a,2}}{p_1 \cdots p_{\ell-1}} (\log X)^{-A/9} + \Omega, \end{align*}$$
with A arbitrarily large. Note that
![]() $p_1 \cdots p_{\ell -1} \leq X$
, and hence
$p_1 \cdots p_{\ell -1} \leq X$
, and hence
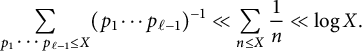 $$\begin{align*}\sum_{p_1 \cdots p_{\ell-1} \leq X} (p_1 \cdots p_{\ell-1})^{-1} \ll \sum_{n \leq X} \frac{1}{n} \ll \log X. \end{align*}$$
$$\begin{align*}\sum_{p_1 \cdots p_{\ell-1} \leq X} (p_1 \cdots p_{\ell-1})^{-1} \ll \sum_{n \leq X} \frac{1}{n} \ll \log X. \end{align*}$$
Hence,
Choosing A large shows that this contribution is negligible.
The remaining case can be summarized by the following properties:
-
(1)
 $\prod _{i,j} A_{ij} \leq \Delta ^{-6} X$
.
$\prod _{i,j} A_{ij} \leq \Delta ^{-6} X$
. -
(2)
 $A_{ij} \geq X^\ddagger $
for at least three pairs of indices
$A_{ij} \geq X^\ddagger $
for at least three pairs of indices
 $(i,j)$
.
$(i,j)$
. -
(3) If
 $A_{ij}, A_{k\ell } \geq X^\dagger $
, then
$A_{ij}, A_{k\ell } \geq X^\dagger $
, then
 $j = \ell $
.
$j = \ell $
. -
(4) If
 $A_{ij} \leq A_{k \ell }$
with
$A_{ij} \leq A_{k \ell }$
with
 $j \ne \ell $
, then either
$j \ne \ell $
, then either
 $A_{ij} = 1$
or
$A_{ij} = 1$
or
 $2 \leq A_{ij} \leq X^\dagger $
and
$2 \leq A_{ij} \leq X^\dagger $
and
 $A_{k \ell } < X^\ddagger $
.
$A_{k \ell } < X^\ddagger $
.
We now show that the second option in (4) cannot happen. This will imply that we have accounted for all possibilities for (7.11), and hence reduced our problem to estimating
![]() ${\mathcal {S}}_1(X)$
.
${\mathcal {S}}_1(X)$
.
Suppose, without loss of generality, that
![]() $2 \leq A_{11} \leq X^\dagger $
and
$2 \leq A_{11} \leq X^\dagger $
and
![]() $A_{22} < X^\ddagger $
. Since
$A_{22} < X^\ddagger $
. Since
![]() $A_{ij} \geq X^\ddagger $
for at least three pairs of indices
$A_{ij} \geq X^\ddagger $
for at least three pairs of indices
![]() $(i,j)$
, one of
$(i,j)$
, one of
![]() $A_{12}$
or
$A_{12}$
or
![]() $A_{32}$
must exceed
$A_{32}$
must exceed
![]() $X^\ddagger $
. We then have
$X^\ddagger $
. We then have
![]() $A_{11} \leq X^\dagger $
and
$A_{11} \leq X^\dagger $
and
![]() $A_{32}$
, say, exceeds
$A_{32}$
, say, exceeds
![]() $X^\ddagger $
, which means that our earlier estimation covers this case.
$X^\ddagger $
, which means that our earlier estimation covers this case.
The upshot now is that
for some
![]() $\kappa (A)> 0$
. It follows from (7.12) that
$\kappa (A)> 0$
. It follows from (7.12) that
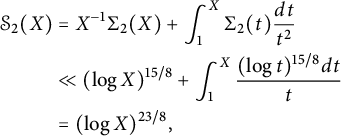 $$ \begin{align*} {\mathcal{S}}_2(X) & = X^{-1} \Sigma_2(X) + \int_1^X \Sigma_2(t) \frac{dt}{t^2} \\ & \ll (\log X)^{15/8} + \int_1^X \frac{(\log t)^{15/8} dt}{t} \\ & = (\log X)^{23/8}, \end{align*} $$
$$ \begin{align*} {\mathcal{S}}_2(X) & = X^{-1} \Sigma_2(X) + \int_1^X \Sigma_2(t) \frac{dt}{t^2} \\ & \ll (\log X)^{15/8} + \int_1^X \frac{(\log t)^{15/8} dt}{t} \\ & = (\log X)^{23/8}, \end{align*} $$
which is sufficiently small for our purposes.
Finally, we may evaluate the main term, which is given by (7.10). By the triangle inequality, we have
 $$\begin{align*}{\mathcal{S}}_1(X) \ll \sum_{x_1 x_2 x_3 \leq X} \frac{1}{x_1 x_2 x_3} = \sum_{n \leq X} \frac{d_3(n)}{n},\end{align*}$$
$$\begin{align*}{\mathcal{S}}_1(X) \ll \sum_{x_1 x_2 x_3 \leq X} \frac{1}{x_1 x_2 x_3} = \sum_{n \leq X} \frac{d_3(n)}{n},\end{align*}$$
which is
![]() $O((\log X)^3)$
. This completes the proof of the proposition.
$O((\log X)^3)$
. This completes the proof of the proposition.
7.2.3 Lower bounds
For the lower bound, it suffices to give an accurate count for some subset of the points enumerated by the quantity
![]() $N_2(T)$
. The arguments used here are inspired by the work of the second author and C.L. Stewart in [Reference Stewart and Xiao19], though the situation here is slightly simpler. To wit, we shall consider the subset of points
$N_2(T)$
. The arguments used here are inspired by the work of the second author and C.L. Stewart in [Reference Stewart and Xiao19], though the situation here is slightly simpler. To wit, we shall consider the subset of points
![]() $({\mathbf {x}}, {\mathbf {y}})$
satisfying the condition
$({\mathbf {x}}, {\mathbf {y}})$
satisfying the condition
where
![]() $\delta $
is some explicit positive number which we shall specify later. Next, we suppose that
$\delta $
is some explicit positive number which we shall specify later. Next, we suppose that
![]() $x_1, x_2$
satisfy
$x_1, x_2$
satisfy
Note that
whence
Thus,
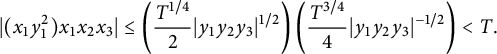 $$\begin{align*}|(x_1 y_1^2) x_1 x_2 x_3| \leq \left(\frac{ T^{1/4}}{2} |y_1 y_2 y_3|^{1/2} \right) \left(\frac{ T^{3/4}}{4} |y_1 y_2 y_3|^{-1/2} \right) < T. \end{align*}$$
$$\begin{align*}|(x_1 y_1^2) x_1 x_2 x_3| \leq \left(\frac{ T^{1/4}}{2} |y_1 y_2 y_3|^{1/2} \right) \left(\frac{ T^{3/4}}{4} |y_1 y_2 y_3|^{-1/2} \right) < T. \end{align*}$$
Therefore, every pair
![]() $(x_1, x_2)$
satisfying (7.17) with
$(x_1, x_2)$
satisfying (7.17) with
![]() $x_1, x_2$
both square-free and
$x_1, x_2$
both square-free and
![]() $x_3 = (y_1^2 x_1 + y_2^2 x_2) y_3^{-2} \in {\mathbb {Z}}$
square-free will contribute to
$x_3 = (y_1^2 x_1 + y_2^2 x_2) y_3^{-2} \in {\mathbb {Z}}$
square-free will contribute to
![]() $N_2(T)$
.
$N_2(T)$
.
We now count pairs
![]() $(x_1, x_2)$
such that:
$(x_1, x_2)$
such that:
-
(1)
 $(x_1, x_2)$
satisfies (7.17);
$(x_1, x_2)$
satisfies (7.17); -
(2)
 $\gcd (x_1, x_2) = 1$
;
$\gcd (x_1, x_2) = 1$
; -
(3)
 $x_1, x_2$
are square-free; and
$x_1, x_2$
are square-free; and -
(4)
 $y_1^2 x_1 + y_2^2 x_2 \equiv 0 \pmod {y_3^2}$
,
$y_1^2 x_1 + y_2^2 x_2 \equiv 0 \pmod {y_3^2}$
,
 $(y_1^2 x_1 + y_2^2 x_2)y_3^{-2}$
is square-free.
$(y_1^2 x_1 + y_2^2 x_2)y_3^{-2}$
is square-free.
For each prime p, we interpret conditions (2)–(4) modulo
![]() $p^2$
. Condition (2) is the assertion that
$p^2$
. Condition (2) is the assertion that
![]() $p | x_1 \Rightarrow p \nmid x_2$
, Condition (3) is the assertion that for all primes p we have
$p | x_1 \Rightarrow p \nmid x_2$
, Condition (3) is the assertion that for all primes p we have
![]() $p^2 \nmid x_1, x_2$
, and condition (4) is stating
$p^2 \nmid x_1, x_2$
, and condition (4) is stating
![]() $y_3^2 | y_1^2 x_1 + y_2^2 x_2$
, and if
$y_3^2 | y_1^2 x_1 + y_2^2 x_2$
, and if
![]() $p^{s} || y_3$
, then
$p^{s} || y_3$
, then
![]() $p^{2s + 2} \nmid y_1^2 x_1 + y_2^2 x_2$
. Let
$p^{2s + 2} \nmid y_1^2 x_1 + y_2^2 x_2$
. Let
It is apparent that
![]() $\rho _{\mathbf {y}}(\cdot )$
is multiplicative. Put
$\rho _{\mathbf {y}}(\cdot )$
is multiplicative. Put
and
By standard arguments using the inclusion–exclusion sieve, we have
 $$\begin{align*}N^\ast({\mathbf{y}}; T) = \prod_{p \leq Y} \left(1 - \frac{\rho_{\mathbf{y}}(p^{2k})}{p^{2k}} \right) \frac{T^{1/2} }{|y_1 y_2 y_3|} + O \left(\sum_{Y < p < T^{1/8} |y_1 y_2 y_3|^{1/4} \max\{|y_1|^{-1},|y_2|^{-1}\}} \left(\frac{T^{1/2}}{p^2 |y_1 y_2 y_3|} + 1 \right) \right), \end{align*}$$
$$\begin{align*}N^\ast({\mathbf{y}}; T) = \prod_{p \leq Y} \left(1 - \frac{\rho_{\mathbf{y}}(p^{2k})}{p^{2k}} \right) \frac{T^{1/2} }{|y_1 y_2 y_3|} + O \left(\sum_{Y < p < T^{1/8} |y_1 y_2 y_3|^{1/4} \max\{|y_1|^{-1},|y_2|^{-1}\}} \left(\frac{T^{1/2}}{p^2 |y_1 y_2 y_3|} + 1 \right) \right), \end{align*}$$
the error term being bounded by
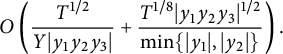 $$\begin{align*}O \left(\frac{T^{1/2}}{Y |y_1 y_2 y_3|} + \frac{T^{1/8} |y_1 y_2 y_3|^{1/2}}{\min\{|y_1|, |y_2|\}} \right). \end{align*}$$
$$\begin{align*}O \left(\frac{T^{1/2}}{Y |y_1 y_2 y_3|} + \frac{T^{1/8} |y_1 y_2 y_3|^{1/2}}{\min\{|y_1|, |y_2|\}} \right). \end{align*}$$
Since
![]() $|y_1 y_2 y_3| \leq T^\delta $
, we obtain an acceptable error term provided that
$|y_1 y_2 y_3| \leq T^\delta $
, we obtain an acceptable error term provided that
![]() $\delta < 1/4$
. This shows that
$\delta < 1/4$
. This shows that
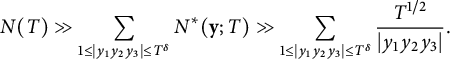 $$\begin{align*}N(T) \gg \sum_{1 \leq |y_1 y_2 y_3| \leq T^\delta} N^\ast({\mathbf{y}}; T) \gg \sum_{1 \leq |y_1 y_2 y_3| \leq T^\delta} \frac{T^{1/2}}{|y_1 y_2 y_3|}.\end{align*}$$
$$\begin{align*}N(T) \gg \sum_{1 \leq |y_1 y_2 y_3| \leq T^\delta} N^\ast({\mathbf{y}}; T) \gg \sum_{1 \leq |y_1 y_2 y_3| \leq T^\delta} \frac{T^{1/2}}{|y_1 y_2 y_3|}.\end{align*}$$
Since
this confirms the lower bound.
7.3 Counting points with respect to the canonical height when
 $\chi (\mathfrak {X}) < 0$
$\chi (\mathfrak {X}) < 0$
In this section, we first prove that the number of quadratic points on a hyperelliptic curve given by the model
where F is an integral, non-singular binary form having degree
![]() $2g+2$
with
$2g+2$
with
![]() $g \geq 2$
, is dominated by the “obvious” points given by triples
$g \geq 2$
, is dominated by the “obvious” points given by triples
![]() $(x,y, \sqrt {F(x,y)})$
. To show that the proper quadratic points are negligible, we note that when
$(x,y, \sqrt {F(x,y)})$
. To show that the proper quadratic points are negligible, we note that when
![]() $g = 2$
the proper quadratic points, which come in conjugate pairs, are in bijection with the rational points of the Jacobian
$g = 2$
the proper quadratic points, which come in conjugate pairs, are in bijection with the rational points of the Jacobian
![]() $\operatorname {Jac}(C_F)$
via the correspondence
$\operatorname {Jac}(C_F)$
via the correspondence
![]() $[P] \mapsto [P_1 + P_2] - K_{C_F}$
, where
$[P] \mapsto [P_1 + P_2] - K_{C_F}$
, where
![]() $K_{C_F}$
is the canonical divisor. Thus, in this case, the proper quadratic points of bounded height are given by the rational points of bounded height in
$K_{C_F}$
is the canonical divisor. Thus, in this case, the proper quadratic points of bounded height are given by the rational points of bounded height in
![]() $\operatorname {Jac}(C_F)({\mathbb {Q}})$
, for which there are
$\operatorname {Jac}(C_F)({\mathbb {Q}})$
, for which there are
![]() $O_F((\log T)^{r_F})$
many, where
$O_F((\log T)^{r_F})$
many, where
![]() $r_F$
is the Mordell–Weil rank of
$r_F$
is the Mordell–Weil rank of
![]() $\operatorname {Jac}(C_F)$
. For
$\operatorname {Jac}(C_F)$
. For
![]() $g \geq 3$
, the proper quadratic points are finite by Faltings’ theorem. Thus, the number of quadratic points on
$g \geq 3$
, the proper quadratic points are finite by Faltings’ theorem. Thus, the number of quadratic points on
![]() $C_F$
is asymptotically equal to the number of rational points in
$C_F$
is asymptotically equal to the number of rational points in
![]() ${\mathbb {P}}_{\mathbb {Q}}^1$
of bounded height.
${\mathbb {P}}_{\mathbb {Q}}^1$
of bounded height.
To the contrary, for
![]() $\mathfrak {X} = \mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}, {\mathbf {m}}))$
with
$\mathfrak {X} = \mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}, {\mathbf {m}}))$
with
![]() $\chi (\mathfrak {X}) < 0$
, we get a much less reasonable result. This is because we have little control over the set of integers
$\chi (\mathfrak {X}) < 0$
, we get a much less reasonable result. This is because we have little control over the set of integers
![]() $x,y$
such that
$x,y$
such that
![]() $\ell _i(x,y)$
is divisible by a large square for
$\ell _i(x,y)$
is divisible by a large square for
![]() $i = 1, \ldots , n$
. Even with the
$i = 1, \ldots , n$
. Even with the
![]() $abc$
-conjecture, there is only so much that can be shown. In the case when
$abc$
-conjecture, there is only so much that can be shown. In the case when
![]() ${\mathbf {m}} = (2, \ldots , 2)$
, we have the following.
${\mathbf {m}} = (2, \ldots , 2)$
, we have the following.
Theorem 7.8 Let
![]() $\mathfrak {X} = \mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}, {\mathbf {m}}))$
be a stacky curve with
$\mathfrak {X} = \mathfrak {X}({\mathbb {P}}^1 : ({\mathbf {a}}, {\mathbf {m}}))$
be a stacky curve with
 ${\mathbf {m}} = \underbrace {(2, \ldots , 2)}_n$
with
${\mathbf {m}} = \underbrace {(2, \ldots , 2)}_n$
with
![]() $n \geq 5$
. Let
$n \geq 5$
. Let
![]() $N_{{\mathbf {a}}, n}(T)$
be the number of rational points on
$N_{{\mathbf {a}}, n}(T)$
be the number of rational points on
![]() $\mathfrak {X}$
satisfying
$\mathfrak {X}$
satisfying
![]() $H_{({\mathbf {a}}, {\mathbf {m}})}(x,y) \leq T$
. Assume that the
$H_{({\mathbf {a}}, {\mathbf {m}})}(x,y) \leq T$
. Assume that the
![]() $abc$
-conjecture holds. Then, for any
$abc$
-conjecture holds. Then, for any
![]() $\varepsilon> 0$
, we have
$\varepsilon> 0$
, we have
Proof This is similar to the proof of Theorem 2.6. We conclude from that proof that
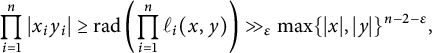 $$\begin{align*}\prod_{i=1}^n |x_i y_i| \geq \operatorname{rad} \left(\prod_{i=1}^n \ell_i(x,y) \right) \gg_{\varepsilon} \max\{|x|, |y|\}^{n-2 - \varepsilon},\end{align*}$$
$$\begin{align*}\prod_{i=1}^n |x_i y_i| \geq \operatorname{rad} \left(\prod_{i=1}^n \ell_i(x,y) \right) \gg_{\varepsilon} \max\{|x|, |y|\}^{n-2 - \varepsilon},\end{align*}$$
and
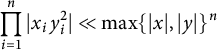 $$\begin{align*}\prod_{i=1}^n |x_i y_i^2| \ll \max\{|x|, |y|\}^n\end{align*}$$
$$\begin{align*}\prod_{i=1}^n |x_i y_i^2| \ll \max\{|x|, |y|\}^n\end{align*}$$
by the triangle inequality. Comparing, we conclude that
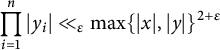 $$\begin{align*}\prod_{i=1}^n |y_i| \ll_{\varepsilon} \max\{|x|, |y|\}^{2 + \varepsilon}\end{align*}$$
$$\begin{align*}\prod_{i=1}^n |y_i| \ll_{\varepsilon} \max\{|x|, |y|\}^{2 + \varepsilon}\end{align*}$$
and in turn
 $$\begin{align*}\prod_{i=1}^n |x_i| \gg_{\varepsilon} \max\{|x|, |y|\}^{n-4 - \varepsilon}.\end{align*}$$
$$\begin{align*}\prod_{i=1}^n |x_i| \gg_{\varepsilon} \max\{|x|, |y|\}^{n-4 - \varepsilon}.\end{align*}$$
It follows that
 $$\begin{align*}H_{({\mathbf{a}}, {\mathbf{m}})}(x,y) = \max\{|x|, |y|\}^{n-4} \prod_{i=1}^n |x_i| \gg_{\varepsilon} \max\{|x|, |y|\}^{2n-8 - \varepsilon}. \end{align*}$$
$$\begin{align*}H_{({\mathbf{a}}, {\mathbf{m}})}(x,y) = \max\{|x|, |y|\}^{n-4} \prod_{i=1}^n |x_i| \gg_{\varepsilon} \max\{|x|, |y|\}^{2n-8 - \varepsilon}. \end{align*}$$
Hence,
![]() $N_{({\mathbf {a}}, {\mathbf {m}})}(T)$
is bounded by the number of rational points in
$N_{({\mathbf {a}}, {\mathbf {m}})}(T)$
is bounded by the number of rational points in
![]() ${\mathbb {P}}_{\mathbb {Q}}^1$
having height at most
${\mathbb {P}}_{\mathbb {Q}}^1$
having height at most
![]() $O_{\varepsilon } \left (T^{\frac {1}{2n-8 - \varepsilon }}\right )$
, which is
$O_{\varepsilon } \left (T^{\frac {1}{2n-8 - \varepsilon }}\right )$
, which is
![]() $O_{\varepsilon } \left (T^{\frac {1}{n-4-\varepsilon }} \right )$
. By adjusting
$O_{\varepsilon } \left (T^{\frac {1}{n-4-\varepsilon }} \right )$
. By adjusting
![]() $\varepsilon $
, we see that
$\varepsilon $
, we see that
Remark 7.9 We do not expect the upper bound given in Theorem 7.8 to be sharp. Indeed, the bound we obtain essentially comes from the scenario that for almost all integers
![]() $m \ll _{\varepsilon } T^{2+\varepsilon }$
that there exist
$m \ll _{\varepsilon } T^{2+\varepsilon }$
that there exist
![]() $x,y$
with
$x,y$
with
![]() $\max \{|x|, |y|\} \ll _{\varepsilon } T^{2 + \varepsilon }$
with
$\max \{|x|, |y|\} \ll _{\varepsilon } T^{2 + \varepsilon }$
with
![]() $Q(x,y)$
divisible by
$Q(x,y)$
divisible by
![]() $m^2$
. We expect that this should not be the case.
$m^2$
. We expect that this should not be the case.
7.4 Hasse principle for integral points when
 ${\mathbf {m}} = (2, 2, 2)$
${\mathbf {m}} = (2, 2, 2)$
We now consider the question of whether the Hasse principle holds for integral points on stacky curves of the shape
![]() $\mathfrak {X} = \mathfrak {X}({\mathbb {P}}_{\mathbb {Q}}^1 : (a_1, a_2, a_3), (2,2,2))$
. By Theorem 3.20 it suffices to consider when it is possible for the stacky part of the height to be equal to one. This is tantamount to requiring the existence of co-prime integers
$\mathfrak {X} = \mathfrak {X}({\mathbb {P}}_{\mathbb {Q}}^1 : (a_1, a_2, a_3), (2,2,2))$
. By Theorem 3.20 it suffices to consider when it is possible for the stacky part of the height to be equal to one. This is tantamount to requiring the existence of co-prime integers
![]() $x,y$
and integers
$x,y$
and integers
![]() $y_1, y_2, y_3$
for which
$y_1, y_2, y_3$
for which
Here, as we recall,
![]() $\ell _i(x,y) = \alpha _i x - \beta _i y$
, with
$\ell _i(x,y) = \alpha _i x - \beta _i y$
, with
![]() $a_i = [\alpha _i : \beta _i]$
. For
$a_i = [\alpha _i : \beta _i]$
. For
![]() $i = 1,2$
, we obtain a system of linear equations
$i = 1,2$
, we obtain a system of linear equations
 $$\begin{align*}\begin{bmatrix} \alpha_1 & - \beta_1 \\ \alpha_2 & -\beta_2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} y_1^2 \\ y_2^2 \end{bmatrix}.\end{align*}$$
$$\begin{align*}\begin{bmatrix} \alpha_1 & - \beta_1 \\ \alpha_2 & -\beta_2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} y_1^2 \\ y_2^2 \end{bmatrix}.\end{align*}$$
Inverting, we find that
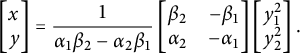 $$\begin{align*}\begin{bmatrix} x \\ y \end{bmatrix} = \frac{1}{\alpha_1 \beta_2 - \alpha_2 \beta_1} \begin{bmatrix} \beta_2 & - \beta_1 \\ \alpha_2 & -\alpha_1 \end{bmatrix} \begin{bmatrix} y_1^2 \\ y_2^2 \end{bmatrix}.\end{align*}$$
$$\begin{align*}\begin{bmatrix} x \\ y \end{bmatrix} = \frac{1}{\alpha_1 \beta_2 - \alpha_2 \beta_1} \begin{bmatrix} \beta_2 & - \beta_1 \\ \alpha_2 & -\alpha_1 \end{bmatrix} \begin{bmatrix} y_1^2 \\ y_2^2 \end{bmatrix}.\end{align*}$$
It follows that
which we can write as
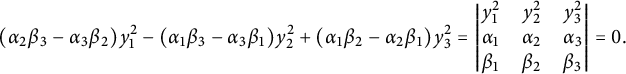 $$\begin{align*}(\alpha_2 \beta_3 - \alpha_3 \beta_2) y_1^2 - (\alpha_1 \beta_3 - \alpha_3 \beta_1) y_2^2 + (\alpha_1 \beta_2 - \alpha_2 \beta_1) y_3^2 = \begin{vmatrix} y_1^2 & y_2^2 & y_3^2 \\ \alpha_1 & \alpha_2 & \alpha_3 \\ \beta_1 & \beta_2 & \beta_3 \end{vmatrix} = 0.\end{align*}$$
$$\begin{align*}(\alpha_2 \beta_3 - \alpha_3 \beta_2) y_1^2 - (\alpha_1 \beta_3 - \alpha_3 \beta_1) y_2^2 + (\alpha_1 \beta_2 - \alpha_2 \beta_1) y_3^2 = \begin{vmatrix} y_1^2 & y_2^2 & y_3^2 \\ \alpha_1 & \alpha_2 & \alpha_3 \\ \beta_1 & \beta_2 & \beta_3 \end{vmatrix} = 0.\end{align*}$$
Therefore, the existence of the integers
![]() $y_1, y_2, y_3$
, and hence
$y_1, y_2, y_3$
, and hence
![]() $x,y$
, depends on whether this conic has a rational point.
$x,y$
, depends on whether this conic has a rational point.
Acknowledgement
We thank J.S. Ellenberg for introducing us to this problem, when he discussed the problem in several lectures, as well his continued interest and encouragement throughout the project. We would also like to thank M. Satriano for explaining the construction of heights on algebraic stacks to us, and for his continuous support and guidance during this project.
Competing interests
As far as we are aware, there are no competing interests involved with this manuscript.
Data availability Statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.