Article contents
Higher Order Tangents to Analytic Varieties along Curves. II
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 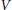 $V$ be an analytic variety in some open set in
$V$ be an analytic variety in some open set in 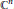 ${{\mathbb{C}}^{n}}$. For a real analytic curve
${{\mathbb{C}}^{n}}$. For a real analytic curve 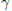 $\gamma $ with
$\gamma $ with  $\gamma (0)\,=\,0$ and
$\gamma (0)\,=\,0$ and 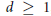 $d\,\ge \,1$, define
$d\,\ge \,1$, define 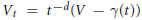 ${{V}_{t}}\,=\,{{t}^{-d}}(V\,-\,\gamma (t))$. It was shown in a previous paper that the currents of integration over
${{V}_{t}}\,=\,{{t}^{-d}}(V\,-\,\gamma (t))$. It was shown in a previous paper that the currents of integration over 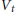 ${{V}_{t}}$ converge to a limit current whose support
${{V}_{t}}$ converge to a limit current whose support 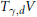 ${{T}_{\gamma ,d}}V$ is an algebraic variety as
${{T}_{\gamma ,d}}V$ is an algebraic variety as 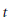 $t$ tends to zero. Here, it is shown that the canonical defining function of the limit current is the suitably normalized limit of the canonical defining functions of the
$t$ tends to zero. Here, it is shown that the canonical defining function of the limit current is the suitably normalized limit of the canonical defining functions of the 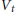 ${{V}_{t}}$. As a corollary, it is shown that
${{V}_{t}}$. As a corollary, it is shown that 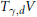 ${{T}_{\gamma ,d}}V$ is either inhomogeneous or coincides with
${{T}_{\gamma ,d}}V$ is either inhomogeneous or coincides with 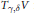 ${{T}_{\gamma ,\,\delta }}V$ for all
${{T}_{\gamma ,\,\delta }}V$ for all 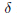 $\delta $ in some neighborhood of
$\delta $ in some neighborhood of 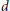 $d$. As another application it is shown that for surfaces only a finite number of curves lead to limit varieties that are interesting for the investigation of Phragmén-Lindelöf conditions. Corresponding results for limit varieties
$d$. As another application it is shown that for surfaces only a finite number of curves lead to limit varieties that are interesting for the investigation of Phragmén-Lindelöf conditions. Corresponding results for limit varieties 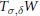 ${{T}_{\sigma ,\delta }}W$ of algebraic varieties
${{T}_{\sigma ,\delta }}W$ of algebraic varieties  $W$ along real analytic curves tending to infinity are derived by a reduction to the local case.
$W$ along real analytic curves tending to infinity are derived by a reduction to the local case.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2008
References
- 1
- Cited by


