No CrossRef data available.
Article contents
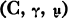 -Homogeneity of Projective Planes and Polarities
-Homogeneity of Projective Planes and Polarities
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In (1) Baer introduced the concept of (C, γ)-transitivity and (C, γ)- homogeneity. A projective plane (see (5) for the requisite definitions and axioms) is (C, γ)-transitive if, given an ordered pair (P 1, P 2) of points collinear with C but distinct from C and not on γ, there is a collineation which maps P 1 into P 2 and leaves fixed every point on γ as well as every line through C. A projective plane is (C, γ)-homogeneous for a non-incident point-line-pair if it is (C, γ) transitive and there is a correlation which maps every line through C into its intersection with γ and every point on γ into its join with C.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1965
References
2.
Barlotti, A., Le possibili configurazioni del sistema delle coppie punto-retta
(A, a) per oui un piano grafico risulta (A, a) transitivo, Boll. U.M.I., 12 (1957), 212–26.Google Scholar
3.
Lenz, H., Kleiner Desargues s cher Satz und Dualität in projektiven Ebenen, Jber. Dtsch. Math. Ver., 57 (1954), 20–31.Google Scholar
4.
Jönsson, W. J., Transitivitdt und Homogenität projektiver Ebenen, Math. Z.7
80 (1963), 269–92.Google Scholar

