Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-08T21:44:13.873Z Has data issue: false hasContentIssue false
  • English
  • Français

Ideals in Rings of Analytic Functions with Smooth Boundary Values

Published online by Cambridge University Press:  20 November 2018

B. A. Taylor  and
D. L. Williams
B. A. Taylor
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, New York Syracuse University, Syracuse, New York
D. L. Williams
Affiliation:
University of Michigan, Ann Arbor, Michigan Syracuse University, Syracuse, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

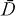Let A denote the Banach algebra of functions analytic in the open unit disc D and continuous in . If f and its first m derivatives belong to A, then the boundary function f(eiθ) belongs to Cm(∂D). The space Am of all such functions is a Banach algebra with the topology induced by Cm(∂D). If all the derivatives of/ belong to A, then the boundary function belongs to C∞(∂D), and the space A∞ all such functions is a topological algebra with the topology induced by C∞(∂D). In this paper we determine the structure of the closed ideals of A∞ (Theorem 5.3).

Beurling and Rudin (see e.g. [7, pp. 82-89; 10]) have characterized the closed ideals of A, and their solution suggests a possible structure for the closed ideals of A∞.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 6 , 01 December 1970 , pp. 1266 - 1283
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Browder, Felix E., On the “edge of the wedge” theorem, Can. J. Math. 15 (1963), 125–131.Google Scholar
2. Lennart, Carleson, Sets of uniqueness for functions regular in the unit circle, Acta Math. 87 (1952), 325–345.Google Scholar
3. Caughran, James G., Factorization of analytic functions with Hp derivative, Duke Math. J. 36 (1969), 153–158.Google Scholar
4. Caughran, James G., Zeros of analytic functions with infinitely differentiable boundary values, Proc. Amer. Math. Soc. 24 (1970), 700–704.Google Scholar
5. Domar, Yngve, On the existence of a largest subharmonic minorant of a given function, Ark. Mat. 3 (1957), 429–440.Google Scholar
6. V. P., Gurariï, The structure of primary ideals in the rings of functions integrable with increasing weight on the half axis, Soviet Math. Dokl. 9 (1968), 209–213.Google Scholar
7. Hoffman, Kenneth, Banach spaces of analytic functions (Prentice-Hall, Englewood Cliffs, N.J., 1962).Google Scholar
8. Kahane, J.-P., Séries de Fourier absolument convergentes, Ergebnisse der Math, und ihrer Grenzgebiete, Band 50 (Springer-Verlag, Berlin, 1970).Google Scholar
9. Novinger, W. P., Holomorphic functions with infinitely differentiable boundary values (to appear in Illinois J. Math.).Google Scholar
10. Rudin, W., The closed ideals in an algebra of analytic functions, Can. J. Math. 9 (1957), 426–434.Google Scholar
11. Laurent, Schwartz, Théorie des distributions (Hermann, Paris, 1966).Google Scholar
12. Taylor, B. A., Some locally convex spaces of entire functions, Proc. Sympos. Pure Math., Vol. 11, pp. 431–467 (Amer. Math. Soc, Providence, R.I., 1968).Google Scholar
13. Taylor, B. A. and Williams, D. L., Zeros of Lipschitz functions analytic in the unit disc (to appear).Google Scholar
14. Wells, J. H., On the zeros of functions with derivatives in H\ and Hx, Can. J. Math. 22 (1970), 342–347.Google Scholar