Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T01:50:24.817Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral Group Rings of Some p-Groups

Published online by Cambridge University Press:  20 November 2018

Jürgen Ritter  and
Sudarshan Sehgal
Jürgen Ritter
Affiliation:
University of Heidelberg, Heidelberg, West Germany
Sudarshan Sehgal
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. The group of units, 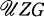, of the integral group ring of a finite non-abelian group G is difficult to determine. For the symmetric group of order 6 and the dihedral group of order 8 this was done by Hughes-Pearson [3] and Polcino Milies [5] respectively. Allen and Hobby [1] have computed 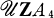, where A4 is the alternating group on 4 letters. Recently, Passman-Smith [6] gave a nice characterization of 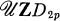where D2p is the dihedral group of order 2p and p is an odd prime. In an earlier paper [2] Galovich-Reiner-Ullom computed 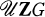when G is a metacyclic group of order pq with p a prime and q a divisor of (p – 1). In this note, using the fibre product decomposition as in [2], we give a description of the units of the integral group rings of the two noncommutative groups of order p3, p an odd prime. In fact, for these groups we describe the components of ZG in the Wedderburn decomposition of QG.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 1 , 01 February 1982 , pp. 233 - 246
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Allen, P. J. and Hobby, C., A characterization of units in Z[AA], J. Algebra 66 (1980), 534–543.Google Scholar
2. Galovich, S., Reiner, I. and Ullom, S., Class groups for integral representations of metacyclic groups, Mathematika 19 (1972), 105–111.Google Scholar
3. Hughes, I. and Pearson, K. R., The group units of the integral group rings Z53, Can. Math. Bull. 15 (1972), 529–534.Google Scholar
4. Huppert, B., Endliche Gruppen I (Springer-Verlag, Heidelberg, 1967).Google Scholar
5. Polcino Milies, C., The units of the integral group ring ZZ)4, Bol. Soc. Brasil. Mat. 4 (1972), 85–92.Google Scholar
6. Passman, D. S. and Smith, P. F., Units in integral group rings, J. Algebra 69 (1981), 213–239.Google Scholar
7. Sehgal, S. K., Topics in group rings (Dekker, New York, 1978).Google Scholar