Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T14:13:09.155Z Has data issue: false hasContentIssue false
  • English
  • Français

L'Enveloppe Conjuguee D'Un Demi-Groupe Inverse a Metacentre Idempotent

Published online by Cambridge University Press:  20 November 2018

Francis Pastijn
Francis Pastijn*
Affiliation:
Dienst Hogere Meetkunde, Rijksuniversiteit te Gent, Gent, Belgique
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Nous renvoyons le lecteur à [4] pour toutes les définitions non expliquées ci-dessous.

Un demi-groupe inverse S est un demi-groupe pour lequel pour tout élément a ∊ S il existe un seul inverse a–1, c'est-à-dire un élément a–l qui satisfait aux conditions aa–1a = a et a–1aa–1 = a–1. Une application λ : S → S, x → λx est appelée une translation à gauche si λ(xy) = (λx)y; une application ρ : S → S, x → xρ est dite translation à droite si (xy)ρ = x(yρ). Les translations à gauche (à droite) forment un demi-groupe Λ(S) [P(S)]. L'ensemble

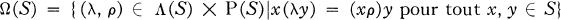
forme un sous-demi-groupe de Λ(S) × P(S) qui est appelé l'enveloppe de translations de S. Si pour tout a ∊ S on définit λa : S → S, x → ax, et ρa : S → S, x → xa, on appelle

la partie interne de Ω(S).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 4 , 01 August 1982 , pp. 900 - 909
Copyright
Copyright © Canadian Mathematical Society 1982

References

References>

1. Munn, W. D., Fundamental inverse semigroups, Quart. J. Math. Oxford (2) 21 (1970), 157–170.Google Scholar
2. Pastijn, F., Essential normal and conjugate extensions of inverse semigroups (à paraître).Google Scholar
3. Petrich, M., On ideals of a semilattice, Czechoslovak Math. J. 22 (1972), 361–367.Google Scholar
4. Petrich, M., Introduction to semigroups (Merrill, Columbus, 1973).Google Scholar
5. Petrich, M., Extensions normales de demi-groupes inverses, Fund. Math. 112 (1981), 187–203.Google Scholar
6. Petrich, M., The conjugate hull of an inverse semigroup, Glasgow Math. J. 21 (1980), 103-124. Math., 33 (1981), 1157–1164.Google Scholar