Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-07T11:50:51.650Z Has data issue: false hasContentIssue false
  • English
  • Français

Localization Theories for Simplicial Presheaves

Published online by Cambridge University Press:  20 November 2018

P. G. Goerss  and
J. F. Jardine
P. G. Goerss
Affiliation:
Mathematics Department, University of Washington, Seattle, WA 98195, USA email: pgoerss@math.washington.edu
J. F. Jardine
Affiliation:
Mathematics Department, University of Western Ontario, London, Ontario, N6A 5B7 email: jardine@uwo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

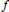Most extant localization theories for spaces, spectra and diagrams of such can be derived from a simple list of axioms which are verified in broad generality. Several new theories are introduced, including localizations for simplicial presheaves and presheaves of spectra at homology theories represented by presheaves of spectra, and a theory of localization along a geometric topos morphism. The $f$-localization concept has an analog for simplicial presheaves, and specializes to the 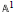${{\mathbb{A}}^{1}}$-local theory of Morel-Voevodsky. This theory answers a question of Soulé concerning integral homology localizations for diagrams of spaces.

Keywords

55P6019E0818F20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 5 , 01 October 1998 , pp. 1048 - 1089
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Artin, M., Grothendieck, A. and Verdier, J-L., SGA4, Theórie des Topos et Cohomologie Étale des Schémas. Lecture Notes in Math. 269, Springer-Verlag, Berlin-Heidelberg-New York, 1972.Google Scholar
2. Bousfield, A.K., The localization of spaces with respect to homology. Topology 14(1975), 133–150.Google Scholar
3. Bousfield, A.K., The localization of spectra with respect to homology. Topology 18(1979), 257–281.Google Scholar
4. Bousfield, A.K., Localization and periodicity in unstable homotopy theory. J. Amer.Math. Soc. 7(1994), 831– 873.Google Scholar
5. Bousfield, A.K. and Friedlander, E.M., Homotopy theory of Γ-spaces, spectra, and bisimplicial sets. Springer Lecture Notes in Math. 658(1978), 80–150.Google Scholar
6. Dror-Farjoun, E., The localization with respect to a map and v1 periodicity. In: Algebraic Topology: Homotopy and Group Cohomology (Eds. J. Aguadé, M. Castellet, and Cohen, F.R.), Springer Lecture Notes in Math. 1509, 1992.Google Scholar
7. Dror-Farjoun, E. , Cellular Spaces, Null Spaces, and Homotopy Localization. Springer Lecture Notes in Math. 1622, 1996.Google Scholar
8. Gillet, H. and Soulé, C., Filtrations on Higher Algebraic K-Theory. Preprint, 1983.Google Scholar
9. Goerss, P.G. and Jardine, J.F., Simplicial Homotopy Theory. Preprint, 1996. http://www.math.uwo.ca/ ∽ jardine/papers/simp-setsGoogle Scholar
10. Hirschhorn, P., Localization, Cellularization, and Homotopy Colimits. Preprint, 1996.Google Scholar
11. Jardine, J.F., Simplicial objects in a Grothendieck topos. Contemporary Math. 55(1986), 193–239.Google Scholar
12. Jardine, J.F., Simplicial presheaves. J. Pure Appl. Algebra 47(1987), 35–87.Google Scholar
13. Jardine, J.F., Stable homotopy theory of simplicial presheaves. Canad. J. Math. 39(1987), 733–747.Google Scholar
14. Jardine, J.F.. Generalized Etale Cohomology Theories. Progr. Math. 146, Birkhäuser, Basel-Boston-Berlin, 1997.Google Scholar
15. Jardine, J.F., Boolean localization, in practice. Doc. Math. 1(1996), 245–275.Google Scholar
16. Mac, S. Lane and Moerdijk, I., Sheaves in Geometry and Logic: A First Introduction to Topos Theory. Springer-Verlag, Berlin Heidelberg New York, 1992.Google Scholar
17. Morel, F. and Voevodsky, V., -local homotopy theory of schemes. Preprint, 1998.Google Scholar
18. Voevodsky, V., The Milnor Conjecture. Preprint, 1996.Google Scholar