Article contents
Metaplectic Tensor Products for Automorphic Representation of 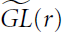 (r)
(r)
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 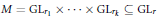 $M\,=\,\text{G}{{\text{L}}_{{{r}_{1}}}}\,\times \,\cdots \,\times \,\text{G}{{\text{L}}_{{{r}_{k}}}}\,\subseteq \,\text{G}{{\text{L}}_{r}}$ be a Levi subgroup of
$M\,=\,\text{G}{{\text{L}}_{{{r}_{1}}}}\,\times \,\cdots \,\times \,\text{G}{{\text{L}}_{{{r}_{k}}}}\,\subseteq \,\text{G}{{\text{L}}_{r}}$ be a Levi subgroup of 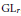 $\text{G}{{\text{L}}_{r}}$, where
$\text{G}{{\text{L}}_{r}}$, where 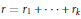 $r\,=\,{{r}_{1}}+\cdots +{{r}_{k}}$, and
$r\,=\,{{r}_{1}}+\cdots +{{r}_{k}}$, and 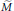 $\widetilde{M}$ its metaplectic preimage in the
$\widetilde{M}$ its metaplectic preimage in the 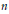 $n$-fold metaplectic cover
$n$-fold metaplectic cover 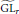 $\widetilde{\text{G}{{\text{L}}_{r}}}$ of
$\widetilde{\text{G}{{\text{L}}_{r}}}$ of 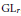 $\text{G}{{\text{L}}_{r}}$. For automorphic representations
$\text{G}{{\text{L}}_{r}}$. For automorphic representations 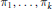 ${{\pi }_{1}},\ldots ,{{\pi }_{k}}$ of
${{\pi }_{1}},\ldots ,{{\pi }_{k}}$ of 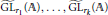 ${{\widetilde{\text{GL}}}_{{{r}_{1}}}}\left( \mathbb{A} \right),\ldots ,{{\widetilde{\text{GL}}}_{{{r}_{k}}}}\left( \mathbb{A} \right)$, we construct (under a certain technical assumption that is always satisfied when
${{\widetilde{\text{GL}}}_{{{r}_{1}}}}\left( \mathbb{A} \right),\ldots ,{{\widetilde{\text{GL}}}_{{{r}_{k}}}}\left( \mathbb{A} \right)$, we construct (under a certain technical assumption that is always satisfied when 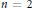 $n\,=\,2$) an automorphic representation
$n\,=\,2$) an automorphic representation 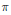 $\pi $ of
$\pi $ of 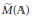 $\widetilde{M}\left( \mathbb{A} \right)$ that can be considered as the “tensor product” of the representations
$\widetilde{M}\left( \mathbb{A} \right)$ that can be considered as the “tensor product” of the representations 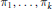 ${{\pi }_{1}},\ldots ,{{\pi }_{k}}$. This is the global analogue of the metaplectic tensor product defined by P. Mezo in the sense that locally at each place
${{\pi }_{1}},\ldots ,{{\pi }_{k}}$. This is the global analogue of the metaplectic tensor product defined by P. Mezo in the sense that locally at each place 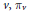 $v,\,{{\pi }_{v}}$ is equivalent to the local metaplectic tensor product of
$v,\,{{\pi }_{v}}$ is equivalent to the local metaplectic tensor product of 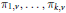 ${{\text{ }\!\!\pi\!\!\text{ }}_{1,\,v}},\ldots ,{{\text{ }\!\!\pi\!\!\text{ }}_{k,\,v}}$ defined by Mezo. Then we show that if all of the
${{\text{ }\!\!\pi\!\!\text{ }}_{1,\,v}},\ldots ,{{\text{ }\!\!\pi\!\!\text{ }}_{k,\,v}}$ defined by Mezo. Then we show that if all of the 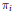 ${{\text{ }\!\!\pi\!\!\text{ }}_{i}}$ are cuspidal (resp. square-integrable modulo center), then the metaplectic tensor product is cuspidal (resp. square-integrable modulo center). We also show that (both locally and globally) the metaplectic tensor product behaves in the expected way under the action of a Weyl group element and show the compatibility with parabolic inductions.
${{\text{ }\!\!\pi\!\!\text{ }}_{i}}$ are cuspidal (resp. square-integrable modulo center), then the metaplectic tensor product is cuspidal (resp. square-integrable modulo center). We also show that (both locally and globally) the metaplectic tensor product behaves in the expected way under the action of a Weyl group element and show the compatibility with parabolic inductions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 11
- Cited by




