Hostname: page-component-5cf477f64f-pw477 Total loading time: 0 Render date: 2025-04-03T17:32:04.950Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicities and Minimal Widths for (0, 1)-Matrices

Published online by Cambridge University Press:  20 November 2018

D. R. Fulkerson  and
H. J. Ryser
D. R. Fulkerson
Affiliation:
The Rand Corporation
H. J. Ryser
Affiliation:
Ohio State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

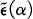In a previous paper (1) the notion of the α-width ∈A(α) of a (0, 1)-matrix A was introduced, and a formula for the minimal α-width taken over the class 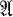of all (0, 1)-matrices having the same row and column sums as A, was obtained. The main tool in arriving at this formula was a block decomposition theorem (1, Theorem 2.1; repeated below as Theorem 2.1) that established the existence, in the class 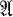generated by A, of certain matrices having a simple block structure. The block decomposition theorem does not itself directly involve the notion of minimal α-width, but rather centres around a related class concept, that of multiplicity. We review both of these notions in § 2, together with some other pertinent definitions and results.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 498 - 508
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Fulkerson, D. R. and Ryser, H. J., Widths and heights of (0, l)-matrices, Can. J. Math. 13 (1961), 239–255.Google Scholar
2. Fulkerson, D. R. and Ryser, H. J., Traces, term ranks, widths and heights, I.B.M. Journal, 4 (1960), 455–459.Google Scholar
3. Gale, D., A theorem onflows in networks, Pac. J. Math., 7 (1957), 1073–1082.Google Scholar
4. Hardy, G. H., Littlewood, J. E., and Polya, G., Inequalities, Cambridge University Press (1952).Google Scholar
5. Muirhead, R. F., Some methods applicable to identities and inequalities of symmetric algebraic functions of n letters, Proc. Edin. Math. Soc, 21 (1903), 144–157.Google Scholar
6. Ryser, H. J., Combinatorial properties of matrices of zeros and ones, Can. J. Math., 9 (1957), 371–377.Google Scholar
7. Ryser, H. J., The term rank of a matrix, Can. J. Math., 10 (1958), 57–65.Google Scholar
8. Ryser, H. J., Traces of matrices of zeros and ones, Can. J. Math., 12 (1960), 463–476.Google Scholar
9. Ryser, H. J., Matrices of zeros and ones, Bull. Amer. Math. Soc, 66 (1960), 442–464.Google Scholar