Let $\mathbb{F}$ be a finite real abelian extension of 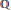$\mathbb{Q}$. Let 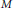$M$ be an odd positive integer. For every squarefree positive integer $r$ the prime factors of which are congruent to 1 modulo 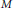$M$ and split completely in $\mathbb{F}$, the corresponding Kolyvagin class 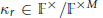${{k}_{r}}\in {{\mathbb{F}}^{\times }}/{{\mathbb{F}}^{\times M}}$ satisfies a remarkable and crucial recursion which for each prime number $\ell $ dividing $r$ determines the order of vanishing of 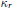${{k}_{r}}$ at each place of $\mathbb{F}$ above $\ell $ in terms of ${{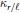k}_{r/\ell }}$. In this note we give the recursion a new and universal interpretation with the help of the double complex method introduced by Anderson and further developed by Das and Ouyang. Namely, we show that the recursion satisfied by Kolyvagin classes is the specialization of a universal recursion independent of $\mathbb{F}$ satisfied by universal Kolyvagin classes in the group cohomology of the universal ordinary distribution à la Kubert tensored with 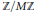$\mathbb{Z}/M\mathbb{Z}$. Further, we show by a method involving a variant of the diagonal shift operation introduced by Das that certain group cohomology classes belonging (up to sign) to a basis previously constructed by Ouyang also satisfy the universal recursion.