Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-09T01:50:59.848Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Family of Generalized Numerical Ranges

Published online by Cambridge University Press:  20 November 2018

C.-S. Lin
C.-S. Lin*
Affiliation:
University of New Brunswick, Fredericton, New Brunswick
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this note, an operator will always mean a bounded linear operator acting on a Hilbert space X into itself, unless otherwise stated. The class Cρ (0 < ρ < ∞ ) of operators, considered by Sz.-Nagy and Foiaş [5], is defined as follows: An operator T is in Cρ if Tnx = pPUnx for all x ∊ X, n = 1, 2, . . . , where U is a unitary operator on some Hilbert space Y containing X as a subspace, and P is the orthogonal projection of Y onto X. In [2] Holbrook defined the operator radii wρ(·) (0 < ρ ≦ ∞ ) as the generalized Minkowski distance functionals on the Banach algebra of bounded linear operators on X, i.e.,

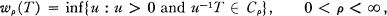
and w∞(T) = r(T), the spectral radius of T [2, Theorem 5.1].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 3 , June 1974 , pp. 678 - 685
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Fillmore, P. A., Note on operator theory (Van Nostrand Reinhold Co., New York, 1970).Google Scholar
2. Holbrook, J. A. R., On the power-bounded operators of Sz.-Nagy and Foias, Acta Sci. Math. (Szeged) 29 (1968), 299–310.Google Scholar
3. Holbrook, J. A. R., Inequalities governing the operator radii associated with unitary ρ-dilations, Michigan Math. J. 18 (1971), 149–159.Google Scholar
4. Halmos, P. R., Hubert space problem book (Van Nostrand, The University Series in Higher Mathematics, 1967).Google Scholar
5. Sz.-Nagy, B. and Foiaş, C., On certain classes of power-bounded operators in Hilbert space, Acta Sci. Math. (Szeged) 27 (1966), 17–25.Google Scholar
6. Orland, G. H., On a class of operators, Proc. Amer. Math. Soc. 15 (1964), 75–79.Google Scholar
7. Stampfli, J. G. and Williams, J. P., Growth conditions and the numerical range in a Banach algebra, Tôhoku Math. J. 20 (1968), 417–424.Google Scholar