Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-08T19:05:07.245Z Has data issue: false hasContentIssue false
  • English
  • Français

On Countability of Point-Finite Families of Sets

Published online by Cambridge University Press:  20 November 2018

Heikki J. K. Junnila
Heikki J. K. Junnila*
Affiliation:
Virginia Polytechnic Institute and State University, Blacksburg, Virginia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that in a separable topological space every point-finite family of open subsets is countable. In the following we are going to show that both in σ-finite measure-spaces and in topological spaces satisfying the countable chain condition, point-finite families consisting of “large” subsets are countable.

Notation and terminology. Let A be a set. The family consisting of all (finite) subsets of A is denoted by 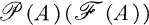. Let 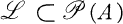be a family of subsets of A. The sets 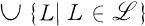and 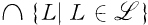are denoted by 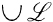and 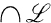, respectively. We say that the family 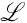is point-finite (disjoint) if for each a ∈ A , the family 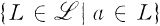has at most finitely many members (at most one member).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 4 , 01 August 1979 , pp. 673 - 679
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Arhangel'skiï, A. V., The property of paracompactness in the class of perfectly normal, locally Mcompact spaces, Soviet Math. Dokl. 12 (1971), 1253–1257.Google Scholar
2. Bing, R. H., Metrization of topological spaces, Can. J. Math. 3 (1951), 175–186.Google Scholar
3. Engelking, R., Outline of general topology (John Wiley & Sons, New York, 1968).Google Scholar
4. Gruenhage, G. and Pfeffer, W. F., When inner regularity of B or el measures implies regularity , preprint.Google Scholar
5. Mazur, S., On continuous mappings on cartesian products, Fund. Math. 39 (1952), 229–238.Google Scholar
6. Michael, E., Point-finite and locally finite coverings, Can. J. Math. 7 (1955), 275–279.Google Scholar
7. Oxtoby, J. C., Measure and category (Springer-Verlag, New York Heidelberg Berlin, 1971).Google Scholar
8. Pixley, C. and Roy, P., Uncompletable Moore spaces, Proceedings of the Auburn Topology Conference, March 1969, Auburn, Alabama, 75–85.Google Scholar
9. Przymusinski, T. and Tall, F. D., The undecidability of the existence of a non-separable normal Moore space satisfying the countable chain condition, Fund. Math. 85 (1974), 291–297.Google Scholar
10. Tall, F. D., The countable chain condition versus separability-applications of Martin s axiom, Gen. Topology and Appl. 4 (1974), 315–339.Google Scholar