Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T13:03:05.005Z Has data issue: false hasContentIssue false
  • English
  • Français

On Maximal Torsion Radicals, II

Published online by Cambridge University Press:  20 November 2018

John A. Beachy
John A. Beachy*
Affiliation:
Indiana University, Bloomington, Indiana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be an associative ring with identity, and let 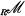denote the category of unital left R-modules. The Walkers [6] raised the question of characterizing the maximal torsion radicals of 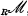, and showed that if R is commutative and Noetherian, then there is a one-to-one correspondence between maximal torsion radicals and minimal prime ideals of R [6, Theorem 1.29]. Popescu announced [5, Theorem 2.5] that the result remains valid for commutative rings with Gabriel dimension (in the terminology of [2]). Theorem 4.6 below shows that the result holds for rings (not necessarily commutative) with Krull dimension on either the left or right, extending the previous theorem for right Noetherian rings which appeared in [1].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 1 , 01 February 1975 , pp. 115 - 120
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Beachy, John A., On maximal torsion radicals, Can. J. Math. 25 (1973), 712–726.Google Scholar
2. Gordon, Robert and Robson, J. C., Krull dimension, Mem. Amer. Math. Soc. (to appear in No. 133, 1973).Google Scholar
3. Lambek, Joachim, Lectures on rings and modules (Blaisdell: Waltham, Toronto, London, 1966).Google Scholar
4. Lambek, Joachim, Torsion theories, additive semantics, and rings of quotients, Lecture Notes in Math 177 (Springer-Verlag, 1971).Google Scholar
5. Popescu, Nicolaie, Les anneaux semi-noetheriens, C. R. Acad. Sci. Paris Ser. A-B 272 (1971), 1439–1441.Google Scholar
6. Walker, Carol L. and Walker, Elbert A., Quotient categories and rings of quotients, Rocky Mountain J. Math. 2 (1972), 513–555.Google Scholar