Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-06-18T17:29:31.782Z Has data issue: false hasContentIssue false
  • English
  • Français

On Meromorphic Operators, II

Published online by Cambridge University Press:  20 November 2018

S. R. Caradus
S. R. Caradus*
Affiliation:
Queen's University, Kingston, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper forms a continuation of (1), extending the concept of a meromorphic operator to not necessarily bounded, closed linear operators in complex Banach space. Let T denote such an operator with range and domain in Banach space X. We shall study the class of such operators T where λ = 0 and λ = ∞ are the only allowable points of accumulation of σ(T) and every isolated point of σ(T) is a pole of Rλ(T). We shall write 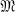(0, ∞) to represent the class of such operators. If λ = 0 (λ = ∞) is the only allowable point of accumulation of σ(T), we shall write 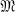(0) (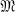(∞)) to denote the corresponding class of operators.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 737 - 748
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Caradus, S. R., On meromorphic operators I, Can. Math, J., (this issue).Google Scholar
2. Caradus, S. R., Operators of Riesz type, Pacific J. Math., 18 (1966), 61–71.Google Scholar
3. Caradus, S. R., Operators with finite ascent and descent, Pacific J. Math., 18 (1966), 437–449.Google Scholar
4. Caradus, S. R., On a theorem of Gohberg and Krein (to be published).Google Scholar
5. Gohberg, I. C. and Krein, M. G., The basic propositions on defect numbers, root numbers and indices of linear operators, Uspehi Mat. Nauk (N.S.), 12 No. 2 (1957), 43–118. (Amer. Math. Soc. Trans. Ser. 2, Vol. 13.)Google Scholar
6. Taylor, A. E., Introduction to functional analysis (New York, 1958).Google Scholar
7. Warner, K. K., Some meromorphic differential operators, Doctoral Dissertation, University of California, Los Angeles, 1965.Google Scholar