Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-22T22:26:16.540Z Has data issue: false hasContentIssue false
  • English
  • Français

On Restriction Estimates for the Zero Radius Sphere over Finite Fields

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  27 February 2020

Alex Iosevich ,
Doowon Koh ,
Sujin Lee ,
Thang Pham  and
Chun-Yen Shen
Alex Iosevich
Affiliation:
Department of Mathematics, University of Rochester New York, Rochester, New York e-mail: iosevich@math.rochester.edu
Doowon Koh
Affiliation:
Department of Mathematics, Chungbuk National University, Cheongju, South Korea e-mail: koh131@chungbuk.ac.kr, sujin4432@chungbuk.ac.kr
Sujin Lee
Affiliation:
Department of Mathematics, Chungbuk National University, Cheongju, South Korea e-mail: koh131@chungbuk.ac.kr, sujin4432@chungbuk.ac.kr
Thang Pham*
Affiliation:
Department of Mathematics, University of Rochester New York, Rochester, New York e-mail: iosevich@math.rochester.edu
Chun-Yen Shen
Affiliation:
Department of Mathematics, National Taiwan University, Taipei, Taiwan e-mail: cyshen@math.ntu.edu.tw
*
e-mail: vpham2@math.rochester.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we completely solve the 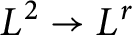$L^{2}\to L^{r}$ extension conjecture for the zero radius sphere over finite fields. We also obtain the sharp 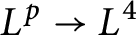$L^{p}\to L^{4}$ extension estimate for non-zero radii spheres over finite fields, which improves the previous result of the first and second authors significantly.

Keywords

Restriction estimatefinite fieldsphere

MSC classification

Primary: 42B05: Fourier series and coefficients
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 3 , June 2021 , pp. 769 - 786
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

A. Iosevich was partially supported by the NSA Grant H98230-15-1-0319. D. Koh was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science, and Technology (NRF-2018R1D1A1B07044469). T. Pham was supported by Swiss National Science Foundation grant P400P2-183916. Chun-Yen Shen was supported in part by MOST through grant 108-2628-M-002-010-MY4.

References

Ahmadi, O. and Mohammadian, A., Sets with many pairs of orthogonal vectors over finite fields. Finite Fields Appl. 37(2016), 179–192. https://doi.org/10.1016/j.ffa.2015.09.009 CrossRefGoogle Scholar
Alon, N. and Spencer, J. H., The probabilistic method. 2nd ed., Wiley-Interscience, 2000. https://doi.org/10.1002/0471722154 CrossRefGoogle Scholar
Barcelo, B., On the restriction of the Fourier transform to a conical surface. Trans. Amer. Math. Soc. 292 (1985), 321–333.Google Scholar
Grove, L. C., Classical groups and geometric algebra. Graduate Studies in Mathematics, 39, American Mathematical Society, Providence, RI, 2002.Google Scholar
Guth, L., A restriction estimate using polynomial partitioning. J. Amer. Math. Soc. 29(2016), no. 2, 371–413. https://doi.org/10.1090/jams827 CrossRefGoogle Scholar
Hart, D., Iosevich, A., Koh, D., and Rudnev, M., Averages over hyperplanes, sum-product theory in vector spaces over finite fields and the Erdős-Falconer distance conjecture. Trans. Amer. Math. Soc. 363(2011), 3255–3275. https://doi.org/10.1090/S0002-9947-2010-05232-8 CrossRefGoogle Scholar
Iosevich, A. and Koh, D., Extension theorems for the Fourier transform associated with non-degenerate quadratic surfaces in vector spaces over finite fields. Illinois J. Math. 52(2008), no.2, 611–628.CrossRefGoogle Scholar
Iosevich, A. and Koh, D., Extension theorems for spheres in the finite field setting. Forum. Math. 22(2010), no.3, 457–483. https://doi.org/10.1515/FORUM.2010.025 CrossRefGoogle Scholar
Iosevich, A., Koh, D., and Lewko, M., Finite field restriction estimates for the paraboloid in high even dimensions. https://arXiv:1712.05549 Google Scholar
Koh, D. and Shen, C., Sharp extension theorems and Falconer distance problems for algebraic curves in two dimensional vector spaces over finite fields. Rev. Mat. Iberoam. 28(2012), no. 1, 157–178. https://doi.org/10.4171/RMI/672 CrossRefGoogle Scholar
Koh, D. and Shen, C., Extension and averaging operators for finite fields. Proc. Edinb. Math. Soc. 56(2013), no. 2, 599–614. https://doi.org/10.1017/S0013091512000326 CrossRefGoogle Scholar
Lewko, M., New restriction estimates for the 3-d paraboloid over finite fields. Adv. Math. 270(2015), no. 1, 457–479. https://doi.org/10.1016/j.aim.2014.11.008 CrossRefGoogle Scholar
Lewko, A. and Lewko, M., Endpoint restriction estimates for the paraboloid over finite fields. Proc. Amer. Math. Soc. 140(2012), 2013–2028. https://doi.org/10.1090/S0002-9939-2011-11444-8 CrossRefGoogle Scholar
Lewko, M., Counting rectangles and an improved restriction estimate for the paraboloid in ${F}_p^3$ . Proc. Amer. Math. Soc. 148(2020), no. 4, 1535–1543. https://doi.org/10.1090/proc/14904 CrossRefGoogle Scholar
Lidl, R. and Niederreiter, H., Finite fields. Encyclopedia of Mathematics and its Applications, 20, Cambridge University Press, Cambridge, 1997.Google Scholar
Mockenhaupt, G. and Tao, T., Restriction and Kakeya phenomena for finite fields. Duke Math. J. 121(2004), 35–74. https://doi.org/10.1215/S0012-7094-04-12112-8 CrossRefGoogle Scholar
Rudnev, M., Point-plane incidences and some applications in positive characteristic. 2018. http://arxiv.org/1806.03534 Google Scholar
Rudnev, M. and Shkredov, I., On the restriction problem for discrete paraboloid in lower dimension. Adv. Math. 339(2018), 657–671. https://doi.org/10.1016/j.aim.2018.10.002 CrossRefGoogle Scholar
Stein, E. M., Some problems in harmonic analysis. In: Harmonic analysis in Euclidean spaces (Proc. Sympos. Pure Math., Williams Coll., Williamstown, Mass., 1978), Part 1, Proc. Sympos. Pure Math., XXXV, Part, Amer. Math. Soc., Providence, R.I., 1979, pp. 3–20.CrossRefGoogle Scholar
Tao, T., A sharp bilinear restriction estimate for paraboloids. Geom. Funct. Anal. 13(2003), 1359–1384. https://doi.org/10.1007/s00039-003-0449-0 CrossRefGoogle Scholar
Tao, T., Some recent progress on the restriction conjecture . In: Fourier analysis and convexity, Appl. Numer. Harmon. Anal., Birkhäuser Boston, Boston, 2004, pp. 217–243.https://doi.org/10.1198/106186003321335099 Google Scholar
Vinh, L. A., A Szemerédi-Trotter type theorem and sum-product estimate over finite fields. European J. Combin. 32(2011), 1177–1181. https://doi.org/10.1016/j.ejc.2011.06.008 CrossRefGoogle Scholar
Vinh, L. A., Maximal sets of pairwise orthogonal vectors in finite fields. Canad. Math. Bull. 55(2012), no. 2, 418–423. https://doi.org/10.4153/CMB-2011-160-x CrossRefGoogle Scholar
Wolff, T., A sharp bilinear cone restriction estimate . Annals of Math. 153(2001), 661–698. https://doi.org/10.2307/2661365 CrossRefGoogle Scholar
Zygmund, A., On Fourier coefficients and transforms of functions of two variables. Studia Math. 50(1974), 189–201. https://doi.org/10.4064/sm-50-2-189-201 CrossRefGoogle Scholar