No CrossRef data available.
Article contents
On some multiplicative properties of large difference sets
Part of:
Ergodic theory
Linear algebraic groups and related topics
Sequences and sets
Forms and linear algebraic groups
Published online by Cambridge University Press: 08 September 2023
Abstract
In our paper, we study multiplicative properties of difference sets 
$A-A$ for large sets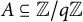 
$A \subseteq {\mathbb {Z}}/q{\mathbb {Z}}$ in the case of composite q. We obtain a quantitative version of a result of A. Fish about the structure of the product sets 
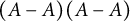$(A-A)(A-A)$. Also, we show that the multiplicative covering number of any difference set is always small.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
References
Bollobás, B., Janson, S., and Riordan, O.,
On covering by translates of a set
. Random Structures Algorithms 38(2011), nos. 1–2, 33–67.10.1002/rsa.20346CrossRefGoogle Scholar
Bourgain, J., The sum-product theorem in
${\mathbb{Z}}_q$
with
$q$
arbitrary. J. Anal. Math. 106(2008), no. 1, 1–93.CrossRefGoogle Scholar
${\mathbb{Z}}_q$
with
$q$
arbitrary. J. Anal. Math. 106(2008), no. 1, 1–93.CrossRefGoogle ScholarBourgain, J. and Gamburd, A.,
Expansion and random walks in
${SL}_d\left(\mathbb{Z}/ {p}^n\mathbb{Z}\right)$
: I
. J. Eur. Math. Soc. 10(2008), 987–1011.CrossRefGoogle Scholar
${SL}_d\left(\mathbb{Z}/ {p}^n\mathbb{Z}\right)$
: I
. J. Eur. Math. Soc. 10(2008), 987–1011.CrossRefGoogle ScholarBourgain, J. and Gamburd, A.,
Uniform expansion bounds for cayley graphs of
${SL}_2\left({F}_p\right)$
. Ann. of Math. 167(2008), 625–642.10.4007/annals.2008.167.625CrossRefGoogle Scholar
${SL}_2\left({F}_p\right)$
. Ann. of Math. 167(2008), 625–642.10.4007/annals.2008.167.625CrossRefGoogle ScholarFish, A.,
On product of difference sets for sets of positive density
. Proc. Amer. Math. Soc. 146(2018), no. 8, 3449–3453.CrossRefGoogle Scholar
Furstenberg, H., Recurrence in ergodic theory and combinatorial number theory. Vol. 10, Princeton University Press, Princeton, NJ, 2014.Google Scholar
Gyarmati, K. and Sárközy, A.,
Equations in finite fields with restricted solution sets. I (character sums)
. Acta Math. Hungar. 118(2008), nos. 1–2, 129–148.CrossRefGoogle Scholar
Gyarmati, K. and Sárközy, A.,
Equations in finite fields with restricted solution sets. II (algebraic equations)
. Acta Math. Hungar. 119(2008), no. 3, 259–280.CrossRefGoogle Scholar
Hart, D., Iosevich, A., and Solymosi, J.,
Sum-product estimates in finite fields via Kloosterman sums
. Int. Math. Res. Not. 9(2007), rnm007.Google Scholar
Pach, P. P.,
Ramsey-type results on the solvability of certain equation in
${\mathbb{Z}}_m$
. Annual 13(2013), 41.Google Scholar
${\mathbb{Z}}_m$
. Annual 13(2013), 41.Google ScholarRuzsa, I.,
An analog of Freiman’s theorem in groups
. Astérisque 258(1999), no. 199, 323–326.Google Scholar
Sárközy, A.,
On sums and products of residues modulo
$p$
. Acta Arithmetica 4(2005), no. 118, 403–409.10.4064/aa118-4-6CrossRefGoogle Scholar
$p$
. Acta Arithmetica 4(2005), no. 118, 403–409.10.4064/aa118-4-6CrossRefGoogle ScholarSchoen, T. and Shkredov, I. D.,
Higher moments of convolutions
. J. Number Theory 133(2013), no. 5, 1693–1737.CrossRefGoogle Scholar
Schur, I.,
Über die kongruenz
${x}^m+{y}^m\equiv {z}^m(modp)$
.
Jahresber. Deutsch. Math. Verein 25(1916), 114–116.Google Scholar
${x}^m+{y}^m\equiv {z}^m(modp)$
.
Jahresber. Deutsch. Math. Verein 25(1916), 114–116.Google ScholarShelah, S.,
Primitive recursive bounds for van der Waerden numbers
. J. Amer. Math. Soc. 1(1988), no. 3, 683–697.10.1090/S0894-0347-1988-0929498-XCrossRefGoogle Scholar
Shkredov, I. D.,
On monochromatic solutions of some nonlinear equations in
$\mathbb{Z}/ p\mathbb{Z}$
. Mat. Zametki 88(2010), 625–634.Google Scholar
$\mathbb{Z}/ p\mathbb{Z}$
. Mat. Zametki 88(2010), 625–634.Google ScholarShkredov, I. D.,
Modular hyperbolas and bilinear forms of Kloosterman sums
. J. Number Theory 220(2021), 182–211.CrossRefGoogle Scholar
Shkredov, I. D., On a girth–free variant of the Bourgain–Gamburd machine. Finite Fields Their Appl. 90(2023), 1–26. https://doi.org/10.1016/j.ffa.2023.102225.CrossRefGoogle Scholar
Shparlinski, I. E.,
On the solvability of bilinear equations in finite fields
. Glasg. Math. J. 50(2008), no. 3, 523–529.CrossRefGoogle Scholar
Stewart, C. L. and Tijdeman, R., On density-difference sets of sets of integers, Birkhäuser, Basel, 1983.10.1007/978-3-0348-5438-2_60CrossRefGoogle Scholar
Tao, T. and Vu, V., Additive combinatorics, Cambridge Studies in Advanced Mathematics, 105, Cambridge University Press, Cambridge, 2006.CrossRefGoogle Scholar
Vinh, L. A.,
The Szemerédi–Trotter type theorem and the sum-product estimate in finite fields
. European J. Combin. 32(2011), no. 8, 1177–1181.CrossRefGoogle Scholar